太阳E10.7 指数的反演及预报方法

雷蕾 钟秋珍 王晶晶 师立勤 苗娟

1(中国科学院国家空间科学中心 北京 100190)

2(中国科学院大学 北京 100049)

0 引言

太阳极紫外辐射EUV（Extreme Ultraviolet）是指波长在10～120 nm 范围的太阳辐射，是中高层大气基本的物理加热能量来源，其扰动变化对地球中高层大气、电离层和空间天气具有重要影响[1,2]。在极紫外漏洞[3]时期，由于测量技术的限制，地面观测的太阳黑子数和10.7 cm 太阳射电流量（F10.7）一直被广泛用于表征地球大气接受的太阳极紫外辐射强度。但实际上太阳黑子数和F10.7对地球大气没有任何直接影响[4,5]。Tobiska[6]通过统计1982 年4 月1 日至1983 年8 月9 日的太阳中层大气探测卫星的日海拔衰减数据，发现F10.7的数值比大气真实接收的极紫外能量高60%或低50%。为有效提升中高层大气模型的精度，提出了一种新的太阳辐射指数E10.7。

E10.7指数是地球大气顶部太阳光谱中波长为1～105 nm 的辐射流量E（t）的积分，并以与F10.7指数一致的单位sfu（1 sfu=10-22W·m-2·Hz-1）给出。表达式为

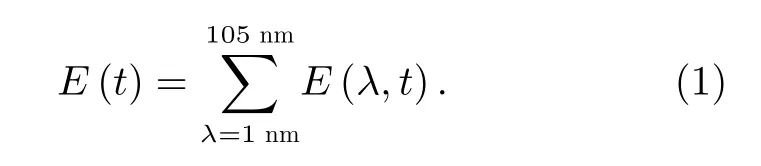
其单位为 J·cm-2·s-1。利用多项式拟合技术，可以将E(t)转化为与F10.7同样的单位，E10.7（单位 sfu）的表达式如下[6]：

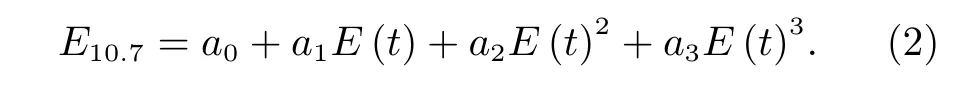
对大气有效加热效应的太阳辐射主要集中在1～105 nm 的波段，因此E10.7是更有效表征太阳活动对中高层大气扰动的代理指数。在针对不同太阳辐射指数对大气模型精度的对比分析中，E10.7的应用可有效提升大气模型的精度[7]。在中国的轨道预报业务中，后续也将应用E10.7。

2000 年美国空间环境技术中心SpaceWX 发布的Solar2000（S2 K）大气辐射模型[8,9]中提供了E10.7指数，可在参考大气模型、电离层模型以及其他模型中来表征太阳活动的强度。美国空军高精度大气拖曳模型（HASDM）的外层温度的表达式中，就采用E10.7替代F10.7来表征外层温度的变化[7]。在针对不同太阳辐射指数对大气模型精度的对比分析中，E10.7的应用可有效提升大气模型精度[10]。已有研究利用30.4 nm 和121.6 nm 的莱曼α 射线两个能道的太阳辐射观测值尝试建立了E10.7计算方法[11]。

在中国的轨道预报业务中，后续也将应用E10.7指数。由于目前中国缺少有效的太阳极紫外观测，无法实时计算得到E10.7，进而提供业务化应用，因此本文利用TIMED-SEE 提供的0.1～105 nm 的太阳辐射强度数据，反演出实时E10.7观测数据，进而开展E10.7的现报和预报研究。

1 E10.7 数据与处理

2002 年在轨运行的TIMED 卫星搭载的太阳极紫外线实验仪（SEE）是首次可以直接测量0.1～194 nm 的太阳极紫外辐射强度的星载仪器，时间跨度为2002 年1 月22 日至今[12]。SEE 由分光计和一套光度计组成，用以测量沉积在大气层的中间层、低热层以及电离层区域的太阳软X 射线、极紫外线和远紫外线辐射。SEE 上的软X 光度计系统由9 个涂有薄膜透射滤光片的硅光电二极管构成，能提供分辨率约5 nm 的1～35 nm 内的软X 光辐照度的测量数据。在25～195 nm 内的光辐照度数据则是由SEE上的极紫外光栅光谱仪测量，分辨率为0.4 nm[13]。

TIMED 卫星SEE 仪器提供0～105 nm 的太阳辐射积分值，为了区分Tobiska 定义的E10.7，以下称为ETS。ETS由戈达德飞行中心的协调数据分析网站（CDA Web）提供*https:--cdaweb.sci.gsfc.nasa.gov-index.html-，时间分辨率约为97 min，单位W·m-2，为准实时数据，数据延迟时间为4 天。为了获取实时E10.7数据，本文利用历史数据建立ETS和E10.7之间的经验关系式，并据此反演得到近实时的E10.7，以通过预报得到未来E10.7预报值，满足大气密度模型和轨道预报的需求。

使用的E10.7数据是美国海洋气象局（NOAA）发布的观测值*https:--cdaweb.sci.gsfc.nasa.gov，时间分辨率为1天，单位为sfu。历史数据的时间跨度为2002 年2 月7日至2006 年6 月30 日。图1 给出了2002 年2 月7 日至2006 年6 月30 日的ETS和E10.7的对比，可以看出二者的波动趋势相似，并且ETS数据在时间分辨率上占绝对优势。

从图1 还可以看出，2002 年中段的ETS部分数据明显偏低，且在ETS数据的某些波峰上方有少许偏高的点（红色点）。前者是由SEE 的某些滤光器异常等导致，后者是由观测仪器在X 级太阳耀斑发生期间响应延迟产生[13]。表1 列出了2002 年2 月7 日至2006年6 月30 日发生的X 级耀斑。本文在后续计算中根据表1 中X 级太阳耀斑发生的峰值时刻剔除这些无效数据。

表1 2002 年2 月7 日至2006 年6 月30 日X 级耀斑Table 1 X class solar flares from 7 February 2002 to 30 June 2006

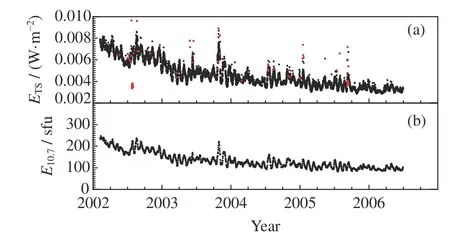
图1 2002 年2 月7 日至2006 年6 月30 日的ETS和E10.7（红色点为异常数据）Fig.1 ETS and E10.7 from 7 February 2002 to 30 June 2006 (The red points are abnormal)

为了分析E10.7和ETS之间的关系，将分辨率97 min的ETS数据进行线性平均得到日均值，缺失的ETS和E10.7数据用相邻两个数据的均值插入补足。通过统计计算可知，E10.7和ETS日均值的线性相关系数为0.986。为了确定E10.7和ETS的关系，采用最小二乘法对E10.7和ETS的日均值进行线性拟合，可以得到E10.7与ETS的对应关系为

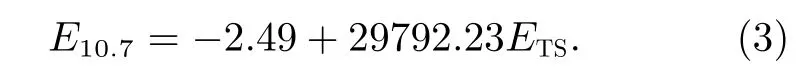
拟合方程的均方根误差为5.724，结果如图2 所示。

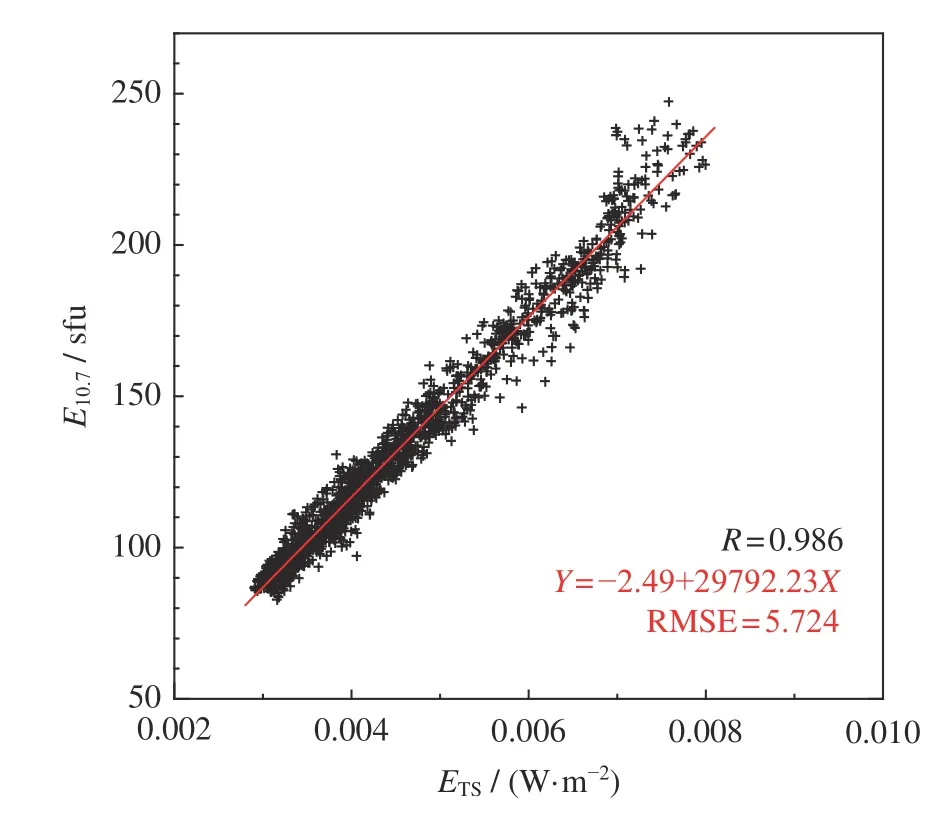
图2 2002 年2 月7 日至2006 年6 月30 日NOAA发布的E10.7与ETS 日均值关系。R 为二者的线性相关系数，RMSE 为线性拟合均方根误差，红色实线为线性拟合结果Fig.2 Relationship between E10.7 and ETS daily average values from 7 February 2002 to 30 June 2006.R is the linear correlation coefficient,RMSE is the root mean square error of linear fitting,and the red solid line is the result of linear fitting

由于TIMED 任务期间存在观测仪器退化等原因，长时间连续观测的ETS数据会受到影响。为了减小这些干扰，采用滑动拟合构建E10.7和ETS日均值的线性关系，即

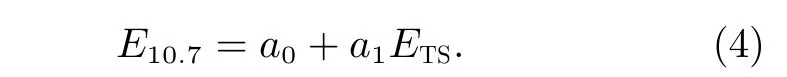
其中，a0和a1分别为线性拟合关系式的常数项和一次项系数。滑动窗口宽度为2 个太阳活动自转周，即54 天。

图3 给出了利用式（3）计算所得的E10.7数据（红色实线）与滑动拟合得到的E10.7数据（蓝色实线，以下称为T10.7）的对比。后者的均方根误差为5.445，低于前者。滑动拟合方法可以排除长时间观测仪器退化对数据的影响，且计算所需数据明显更少，拟合的误差也更低，因此在实际应用中具有明显的优势。这里建模所用数据就是由滑动拟合得到的T10.7。

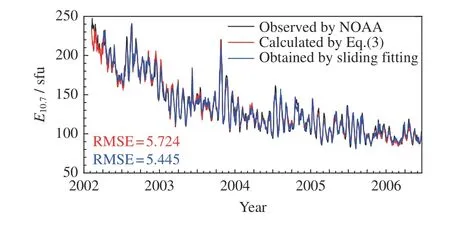
图3 2002 年2 月7 日至2006 年6 月30 日NOAA发布的E10.7 日均值、利用式（3）计算的E10.7 数据及滑动拟合得到的E10.7 数据Fig.3 E10.7 of NOAA calculaed by Eq.(3),and obtained by sliding window linear fitness from 7 February 2002 to 30 June 2006

通过以上方法，得到了与E10.7单位同为sfu的T10.7历史值，数值保留一位小数。这使得后续在各模型中能够更方便地直接应用T10.7数据[6,9]。

2 E10.7 中期预报模型构建

对于E10.7数据这类时间序列，通常能够通过统计方法计算出其相关关系，并利用这个关系来预测未来的数据。常用的预报模型主要包括自回归（Autoregressive，AR）模型、滑动平均（Moving Average，MA）模型以及自回归-滑动平均（Autoregressive Moving Average，ARMA）模型。ARMA 模型的适用性更广，但是其建模计算非常复杂；AR 模型建模相对简单，并且一个高阶的AR 模型可以近似于一个ARMA 模型。因此，本文选择利用高阶自回归模型对E10.7做中期预报。

AR 模型是利用同一变数，例如X的往期即Xt-p至Xt-1来预测本期Xt的表现，并假设其为一线性关系，表达式为

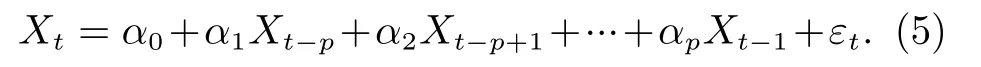
其中，p为AR 模型的阶数；ɛt为白噪声序列，视为预报误差。模型的参数估计采用伯格（Burg）算法[14,15]。

为了确定自回归预报模型的参数和阶数，利用2002 年2 月7 日至2006 年6 月30 日的T10.7数据进行自相关和偏自相关分析。图4 给出了分析结果，可以看出T10.7的自相关系数随天数的增加逐渐减小，并在天数为600 的时候最趋于0；而T10.7的偏自相关系数在52 天时最趋于0，且其后天数的偏自相关系数均在正负0.05 以内。根据自相关系数的分析，T10.7数据的自相关性随着相隔天数的增加下降，600 天时相关系数接近0，即没有相关性。因此，采用连续600 天的观测数据建立自回归模型的样本数据，即用连续600 天的观测数据拟合式（5）中的模型参数。根据偏自相关系数的分析，与当前数据存在独立相关性的数据主要在相隔52 天以内的数据，并且52 天接近两个太阳自转周的时间。因此，预报E10.7自回归模型的阶数选用52 阶。

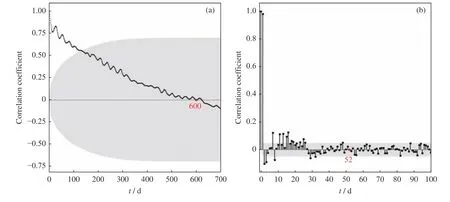
图4 2002 年2 月7 日至2006 年6 月30 日的T10.7 的自相关（a）和偏自相关（b）结果（红色点为相关系数为0 的点）Fig.4 Autocorrelation function (a) and the partial autocorrelation function (b) of T10.7 from 7 February 2002 to 30 June 2006 (Red dot is the point with the correlation coefficient of 0)

实际应用中，通常用E10.7的81 天中心平均值来表示近3 个太阳自转周极紫外辐射的平均状态。本文将过去40 天、未来40 天和当日E10.7的日均值定义为E10.7的81 天中心平均值（E81C），表达式为

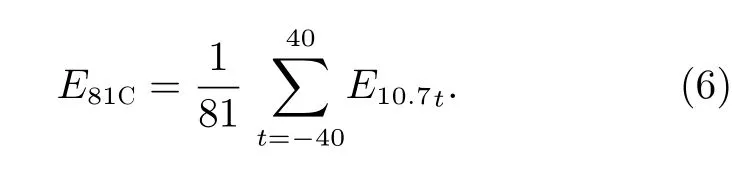
其中，t为距离预报当天的天数。

由于T10.7观测数据有4 天的延迟时间，若采取此数据做预报，在t=-3时，就要开始对T10.7进行预报。对于计算未来第27 天的E81C，需要至未来第67 天的E10.7。因此，需要预报共71 天（t∈[-3,67]）的T10.7。其中前4 天的值为延迟时间内的预报值，5 至31 天的值为未来27 天的预测值，71 天的预报值和实测值用于滑动计算未来27 天的E81C预报值。的预报模型构建流程如下。

第1步利用最小二乘法将过去600 天的E10.7和ETS历史观测数据进行滑动线性拟合，滑动窗口宽度为54，得到共600 天的T10.7数据。

第2步将第1 步所得共600 天的T10.7数据作为训练数据，带入式（5）的52 阶自回归模型，拟合得到自回归模型的参数。

第3步把前52 天的T10.7数据输入自回归模型，计算得到当天的E10.7预报值；以前51天T10.7数据和当天E10.7预报值作为输入，计算得到未来1天E10.7的预报值。以此类推，计算71 天的E10.7预报值。由于T10.7观测数据有4 天的延迟时间，实际应用中，第5 至31 天的值为未来27 天的E10.7预报值。

第4步利用第3 步所得的71天E10.7预报值和E10.7历史实测值，通过式（6）计算未来27 天的E81C预报值。

3 E10.7 预报模型评估

为了评估预报模型的效果，这里以2005 年1 月1 日至2006 年6 月30 日期间的数据为测试集，对E10.7指数进行预报测试。

评估预报结果主要采用逐日相对误差、相对误差、平均逐日相对误差和平均相对误差。其中，逐日相对误差（）为单次预报的未来第t天的相对误差，相对误差（Emr）为单次预报未来27 天的相对误差的平均值，平均逐日相对误差（）为测试集的的平均值，平均相对误差（Emr,av）为全部测试集的Emr的平均值。这4 个量的表达式为

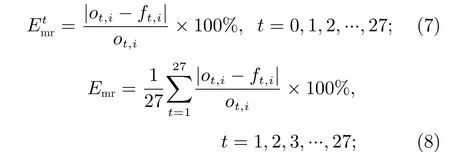
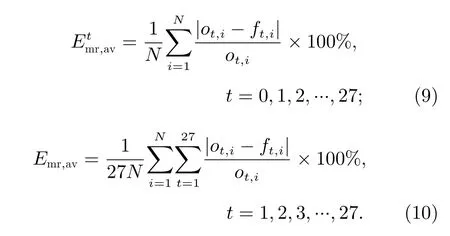
其中，N为测试集样本数，t为预测未来的天数，i为测试集中的单个样本，ot,i为E10.7的实测日值，ft,i为E10.7的预报日值。

利用E10.7自回归预报模型预报2005 年5 月20 日未来67 天的E10.7和未来27 天的E81C，如图5所示。T10.7观测数据有4 天的延迟时间，因此利用式（5）的52 阶自回归模型，共预报71 天（横坐标-3 至67）的T10.7，其中前4 天（横坐标-3 至0）的值为延迟时间内的预报值，5 至31 天（横坐标1 至27）的值为未来27 天的预测值。从图5 可以看出，模型对5 月20 日之后两个太阳自转周内的E10.7的周期变化有较好的预报效果，且未来27 天的E81C预报值与实测值也有较好吻合。模型27天E10.7预报值的平均逐日相对误差为3.05%，模型27 天的E81C预报值平均逐日相对误差为0.62%。

利用E10.7自回归预报模型预报2005 年5 月1 日未来67 天的E10.7和未来27 天的E81C，如图6所示。与图5 相比，本次预报E10.7和E81C的平均逐日相对误差分别增大了10.4% 和7.39%。从图6 可以看出，52 阶自回归预报模型可以很好地确定太阳活动指数的27 天周期，但是预报值与实测值存在一定差距，预报值的周期波动幅度随预报时间增长而减小。因此，当未来27 天的E10.7比前一个周期有增幅时，52 阶自回归预报模型的预报误差较大。

图5 2005 年5 月20 日预报与观测的E10.7和E81C。t 为距2005 年5 月20 日的天数，负值为距2005 年5 月20 日的历史天数Fig.5 E10.7 and E81C that are predicted and observed on 20 May 2005.Positive values in abscissa are the numbers of days after 20 May 2005,the negative values in abscissa are the numbers of days before 20 May 2005

图6 2005 年5 月1 日预报与观测的E10.7和E81C。t 为距离2005 年5 月1 日的天数，负值为距2005 年5 月1 日的历史天数Fig.6 E10.7 and E81C that are predicted and observed on 1 May 2005.Positive values in abscissa are the numbers of days after 1 May 2005,the negative values in abscissa are the numbers of days before 20 May 2005

为衡量自回归模型的整体预报效果，对2005 年1 月1 日至2006 年6 月30 日期间的预报结果进行整体评估。图7 为此期间未来27天E10.7（黑色菱形）和E81C（红色三角）预报结果的平均逐日相对误差。由于T10.7的实测数据存在4 天延时，图中0 天是提前4 天的预报结果，-3 天是提前1 天的预报结果。从图7 可看出，模型E10.7预报值的误差在前7 天内（即提前10 天的预报）较快增长，平均相对误差由3.5%（-3 天）增长到8%（第7 天），7 天至24 天的平均相对误差基本维持在8%附近，24 天后又出现增长。E81C预报值的平均相对误差随预报天数的增加而缓慢增大，从2.5%（-3 天）增加到4.5%（第27 天）。

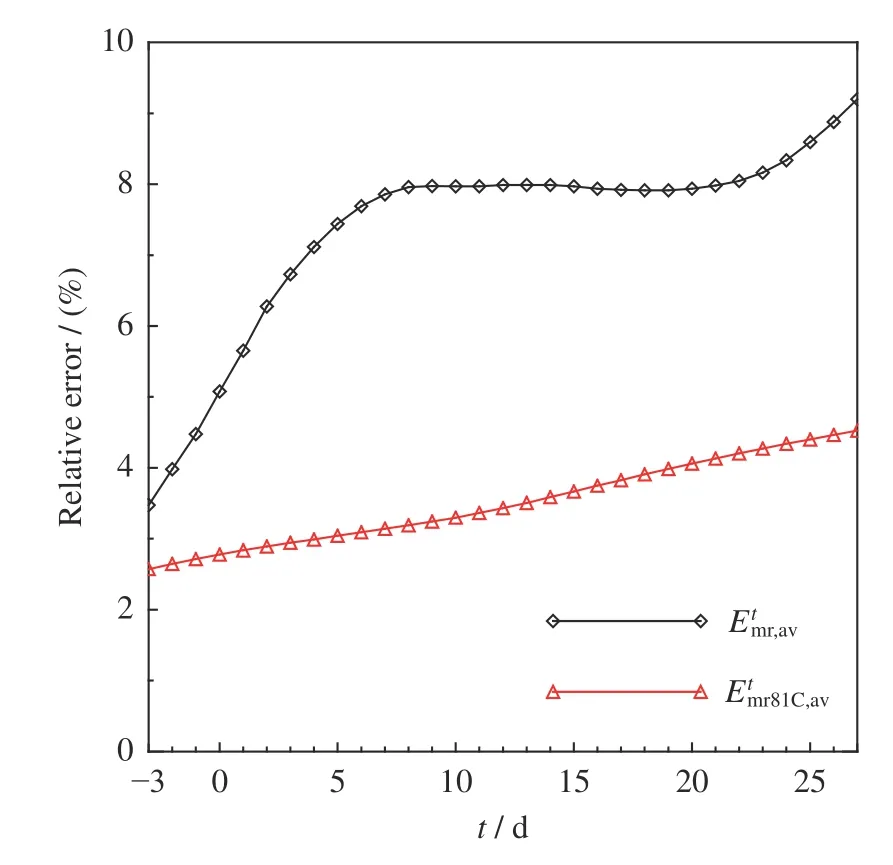
图7 模型预测未来27天E10.7和E81C 的平均逐日相对误差Fig.7 Average daily relative error of E10.7 and E81C that are predicted in the next 27 days

表2 给出了预报结果的误差统计。在整个测试时间段，E10.7预报值27 天平均逐日相对误差最小值为2.4%，最大值为15.08%，平均值为7.83%；E81C预报值27 天平均逐日相对误差最小值为0.29%，最大值为10.10%，平均值为3.63%。对于未来大气模型的应用来说，E81C预报值平均3.63%的误差可以较好地满足应用需求。

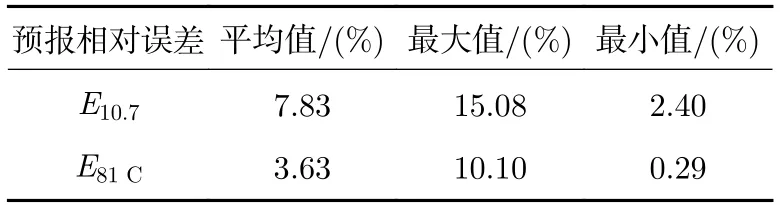
表2 测试集的E10.7和E81C 预报误差Table 2 Predicted error of E10.7 and E81C of all test sets

4 讨论与结论

针对高层大气密度预报和轨道预报业务中对新型太阳紫外辐射指数E10.7的需求，利用TIMED/SEE观测到的高时间分辨率的太阳辐射强度数据，基于最小二乘法建立了反演E10.7指数的方法。在分析反演数据自相关和偏自相关的基础上，构建了一个52 阶的自回归预报模型，可以实现E10.7的中期预报。初步结论如下。

TIMED/SEE 观测仪提供的ETS实测值具有高时间分辨率、延迟时间短和易获得的优势，利用最小二乘法拟合可反演出准实时的E10.7，均方根误差为5.445 sfu，能够基本满足实际应用。利用该方法可以为中国相关用户提供准实时的E10.7指数。

利用52 阶自回归模型对E10.7的中期预报效果尚好，预报误差随预报时间的增加而增大，未来27 天的预报值平均相对误差为7.83%。利用同样方法也开展了对E10.7的81 天滑动平均值E81C的未来27 天预报试验。试验结果表明，与E10.7类似，预报平均相对误差随预报天数的增加而增大，但误差较低，未来27 天的预报值平均相对误差仅为3.63%。

随着航天事业发展，中国卫星轨道预报业务对轨道大气密度的精确度要求也越来越高，将需要逐步在大气模型中采用E10.7指数替代F10.7指数，提高大气密度计算的准确性。本文建立的E10.7反演方法和自回归预报模型可用于未来E10.7的现报和预报。

致谢ETS实测值由TIMED/SEE 观测仪提供。