基于最大似然估计的远紫外遥感反演电离层电子密度算法*

冯桃君 于钱 张凯

(北京卫星环境工程研究所 北京 100094)

0 引言

电离层扰动会对卫星通信和全球定位系统（Global Position System，GPS）产生严重影响，使得建立电离层模型与预报电离层行为变得十分重要，逐步发展出了地基与天基两种探测技术[1]。地基电离层探测技术发展比较成熟，目前已建成的电离层观测站可以对全球范围内很多重要区域进行电离层观测记录。天基电离层探测技术手段主要包括无线电和光学两种，无线电探测中最为典型的代表是GPS 掩星技术[2,3]。星载远紫外（Far Ultraviolet,FUV）遥感是近20 多年来发展起来的一项技术，其优势是地球大气的吸收作用可提供无FUV 的观测背景[4]。另外，相较于地基和GPS 掩星探测，星载远紫外遥感可以实现全球范围的连续观测。

在地球大气的远紫外气辉中，原子氧OI 135.6 nm被广泛应用于各个卫星的观测实验中，夜间OI 135.6 nm 主要由氧离子O+和电子e-的辐射复合反应产生[4]，导致OI 135.6 nm 夜气辉的辐射强度与电子密度的平方正相关[5,6]。从21 世纪初开始，先后在DMSP[7]，IMAGE[8]，TIMED[9]和SES-14[10]等卫星上搭载了远紫外气辉测量仪器，开展对地球高层大气与电离层的遥感探测。DeMajistre等[11]利用正则化的最小二乘法，从搭载在TIMED 上的GUVI 成像仪临边观测的135.6 nm 辐射强度反演得到了夜间电离层电子密度分布（Electron Density Profile,EDP）。搭载在COSMIC 卫星上的光度计TIP 利用135.6 nm辐射强度与峰值电子密度的线性关系获得了峰值电子密度[6]，TIP 观测数据结合COSMIC 上的掩星实验GOX 能重建电离层二维结构[12]。综上研究表明，对夜间135.6 nm 气辉辐射的遥感观测能反演获得电离层电子密度分布，能进一步预测分析与电离层相关的空间天气。然而，中国对电离层的紫外遥感观测及其反演问题的研究才刚刚兴起。

本文分析了135.6 nm 夜气辉的辐射机制，基于计算辐射强度的前向模型，通过模拟仿真验证了最大似然估计法反演电子密度高度分布的可行性。进而将该算法应用于GUVI 夜间临边实测数据，反演得到了电子密度高度分布。

1 夜间135.6 nm 夜气辉辐射机理

根据夜气辉辐射产生的光化学过程可知，夜间电离层的OI 135.6 nm 气辉辐射主要是由O+与电子的辐射复合过程产生，即

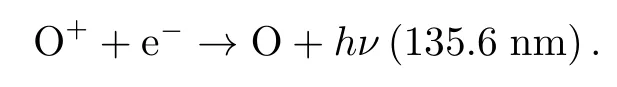
很小一部分来自O+与O-的中和反应。辐射复合反应产生激发态的原子氧O（5S2）在返回基态O（3P2,1）时，会伴随135.6 nm 的双谱线辐射，线中心分别位于135.5598 nm 和135.8512 nm[4,13]。

辐射复合及中和反应产生的OI 135.6 nm 夜气辉体发射率在高度z上的分布可表示为

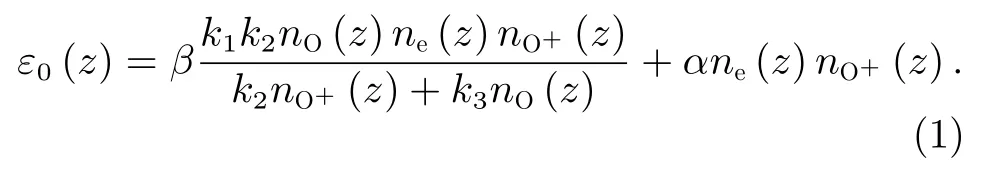
式中，α=7.5×10-13cm3·s-1，为辐射复合速率；β=0.54，为中和反应中生成激发态原子氧的反应所占比例；反应系数k1，k2，k3分别为1.3×10-15cm3·s-1，10-7cm3·s-1和1.4×10-10cm·s-1；nO（z），ne（z）和nO+（z）分别代表氧原子、电子及氧离子密度[12,14]。

由于中和反应贡献比较少，为了简化计算，不考虑中和反应。135.6 nm 在100 km 处的光学深度约为1[14,15]，可视为光学薄线，计算中忽略辐射传输效应。此外，电离层整体呈电中性，且电离层F 区的O+密度与电子密度可认为近似相等，即ne（z）≈nO+（z），但该假设仅适用于约200～500 km 的电离层。对于500 km 以上的电离层，H+逐渐成为主要离子成分，对于200 km 以下的电离层，O2+和NO+等离子成分变得不可忽略[1]。

基于以上假设，电离层F 区的OI 135.6 nm 夜气辉体发射率可以简化为

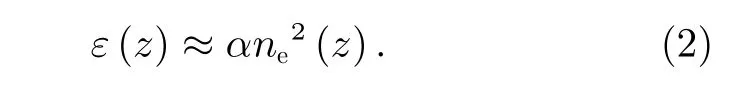
一旦获得体发射率的分布，星载探测器测量的夜气辉OI 135.6 nm 辐射强度I（单位瑞利数Ra）是体发射率沿视线路径的积分，有

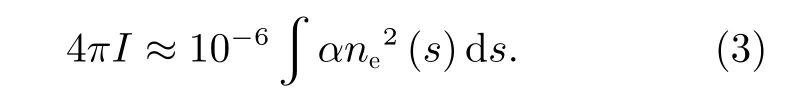
式中，s为沿视线方向到探测器的距离。

2 反演算法

为计算辐射强度，将式（3）离散化，即将卫星高度下方的电离层在垂直方向上分成L层，并假设每层的电子密度是一常数,这样将式（3）可以改写为如下离散形式：

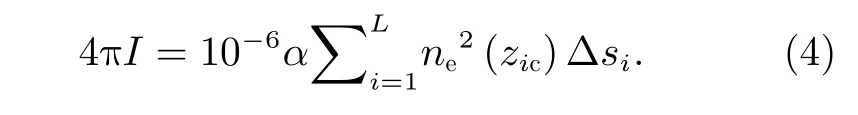
式中，zic为第i层的中心高度，Δsi为视线在第i层的截距。在离散前向模型中，用Chapman 三参数函数表示电子密度的高度分布，有

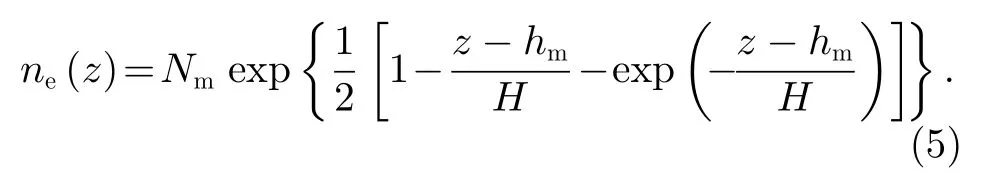
其中，Nm为峰值电子密度，hm为峰值高度，z为海拔高度，H为原子氧标高[12,14]。

离散化后，电离层参数与观测数据之间的关系式（4）可广义地表示为

其中，m为模型参数矢量，其长度为M；d为观测数据矢量，其长度为N，而N个离散的观测数据点对应N个不同的观测角。G为矢量函数，表征了模型参数与数据之间的映射关系[16,17]。在本文中，m=[Nm,hm,H]，M=3，式（6）关于m是一个非线型模型。

观测数据的测量误差往往可看作高斯分布，则观测数据的概率可表示为

其中，do为 观测数据，dt为 模型真值，covdt为数据的协方差矩阵。由于各个观测值是相互独立的，所以covdt是一个对角线矩阵，对角线元素是各观测值标准差σj(j=1,2,···,N)的平方。最大似然估计法就是找到使概率P(do) 最大的模型参数me，该me称为模型参数m的最大似然估计[17]。概率P(do)最大等效为使统计量χ2最小，即

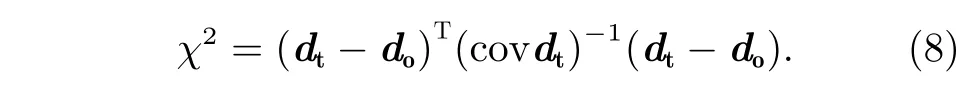
由于前向模型关于m是非线型的，本文使用Levenberg-Marquardt 迭代法求解参数的最大似然估计me[18,19]。首先，选择参数的迭代初始值m0，代入前向模型计算获得辐射强度真值dt；然后，通过式（8）计算得到χ2，并按Levenberg-Marquardt 方法获得下一步计算的参数m1。依此类推，直到第k步的χ2比第k-1 步的小且χ2的变化量小于0.1% 时，迭代停止，mk作 为参数的最大似然估计me。

3 反演算法验证

为验证该算法的可行性，首先仿真计算TIMED卫星上GUVI 的临边观测值。TIMED 卫星运行在625 km 的圆形轨道，倾角74.1°。GUVI 的视场为11.8°，探测器在沿轨方向包含了14 个探测像元，工作时扫描镜在与轨道垂直的方向上进行临边和天底扫描。临边扫描是从与天底方向成+80°夹角开始到+67.2°夹角结束（“+”表示远离太阳的一侧），步长为0.4°，在12.8°的临边范围内有32 步观测，得到32×14 个探测数据，视线切点高度范围约90～525 km。临边扫描结束后，GUVI 进入天底扫描模式，天底扫描包含159 步，覆盖127.2°的天底范围，如图1 所示[20]。GUVI 在完成一次临边和天底扫描后，扫描镜会迅速回到与天底方向成 +80°夹角的位置，开始新的一次扫描。TIMED 的轨道周期约97 min，一天绕地球15 次实现全球覆盖，每轨可获得约388 次扫描，一次临边扫描数据可反演得到一个电子密度剖面。由于反演过程中假设大气层局部球对称，因此电子密度剖面定位在GUVI 视线切点高度最接近300 km 的位置。

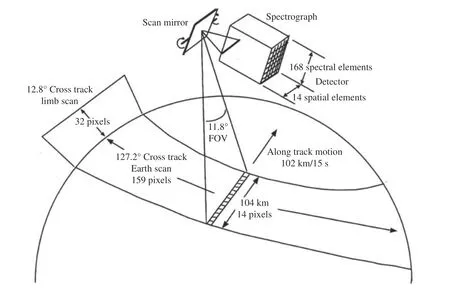
图1 GUVI 的扫描示意Fig.1 Schematic of GUVI’s scan imaging

在建立离散观测模型时，将临边观测视线切点高度覆盖的电离层进行离散化。且为方便后续与GUVI 数据进行比较，这里将海拔高度90～550 km 的电离层分为L=23 层，每层高度为20 km。由于夜间气辉辐射微弱，为提高探测信号的信噪比，每步的观测值取14 个探测像元的平均辐射强度，这样一次临边扫描产生N=32 个观测数据，每个数据点的视线取视场的中心线。在这样的几何观测模式下，测得的135.6 nm 夜气辉辐射强度为

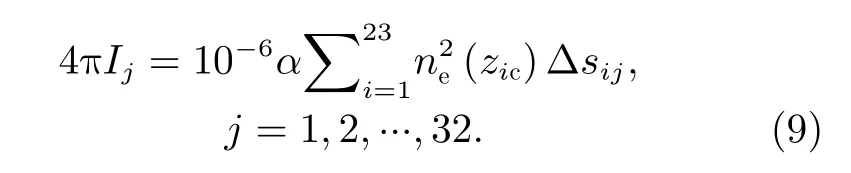
其中，Ij为第j步扫描的辐射强度，与仪器的观测角有关；Δsij为第j步扫描的视线在第i层电离层的截距；zic为第i层电离层的中心高度。按上述分层结构，z1c= 100 km，z2c= 120 km，···，z23c=540 km。ne(zic)为高度zic处的电子密度，可根据式（5）计算得到。式（9）计算出的辐射强度不包含噪声，对于光子计数的仪器而言，噪声产生的不确定度等于探测器计数的开方。为模拟真实的观察值，结合式（5）和式（9）计算得到临边观测无噪声的135.6 nm 夜气辉辐射强度矢量dt，dt包含32Ra的观测值，通过仪器灵敏度与积分时间的乘积（为方便称呼，将该乘积叫作响应度）将dt转换为探测器计数。随机产生一个服从高斯分布的噪声计数。在原计数的基础上添加噪声计数，并将总的计数再转换为以瑞利为单位的包含噪声的辐射强度值do。do作为实际的仪器临边观测数据用于仿真。为验证算法的可行性，本文将电离层参数m=[Nm,hm,H]的真值设置为mt=[1×106cm-3,300 km,50 km]，并从迭代初值、噪声计数和仪器响应度3 个方面分析对反演结果的影响。

3.1 迭代初值

为验证算法的收敛性，进行10 次反演，仪器响应度设为1，每次叠加相同的噪声（即do相同），迭代初值设置为m0=αmt，α为 真值mt的缩放系数，每次反演的缩放系数α从[0.5，1.5]区间均匀随机选择。电子密度的反演结果如图2（a）所示，前向模型计算的相应辐射强度随视线切点高度的分布如图2（b）所示。蓝色实线表示与最大似然估计解me对应的分布；绿色虚线表示与10 次反演结果的均值对应的分布；红线是与真值mt对 应的分布，图2（b）中的dt和do分别代表无噪声和含噪声的辐射强度。图2（a）中10 次反演得到的电子密度分布重叠在一起（蓝线），表明对同一观测数据do，算法的收敛性与迭代初值无关，结果都会收敛到唯一的最大似然估计解。

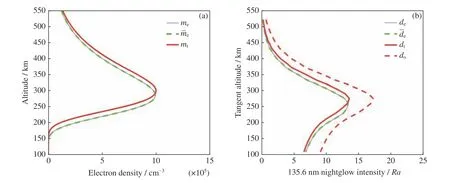
图2 10 次反演结果及反演结果均值与电离层参数真值对应的电子密度高度（a）和 135.6 nm 辐射强度随视线切点高度的分布（b）。10 次反演叠加的噪声相同但迭代初值不同Fig.2 (a) Electron density altitude profiles and (b) 135.6 nm radiation intensity against tangent height of line of sight corresponding to the ten retrieved solutions,mean of solutions,true values of ionospheric parameters.Ten inversion runs have identical noise but different initial guess

3.2 噪声计数

由图2 可知噪声计数使反演结果出现误差，对dt叠加不同的噪声或许会得到不同的反演结果。为研究噪声对反演精度的影响，进行了100 次反演，仪器响应度为1，迭代初值同样设置为m0=αmt，每次反演的α从[0.5,1.5]区间均匀随机选择，但每次对dt随机叠加不同的噪声（即用于反演的do不同）。统计量χ2值随迭代次数的变化如图3 所示，图中每条曲线代表一次反演，由于电离层参数的迭代初值不同，起始χ2在[20，500]区间取得不同的值，在迭代2～4 次后χ2迅速衰减，通常在迭代十几次后收敛，χ2最终减小到10～50 之间。电离层参数的反演结果如图4 所示，可以看出反演结果散布在以真值（红线）为中心的一个区间内，说明叠加不同的噪声会导致不同的反演结果。电离层参数的反演均值（蓝线）为=[1.0144×106cm-3，299.93 km，49.206 km]，电子峰值密度被平均高估了1.44%，峰值高度误差十分小可忽略不计，电离层标高被平均低估了1.59%。图4 还绘制了反演误差离散的概率密度分布统计，横轴被划分为宽度为5%的离散区间。红色曲线是与反演结果的均值和标准差一致的正态分布曲线。可以看出，峰值密度、峰值高度和标高的概率密度分布可近似为中心为0 的正态分布。根据仿真结果，超过90%的峰值密度、峰值高度和标高的误差分别分布在±15%、±5 %和±25%的范围内，对应的峰值密度、峰值高度和标高分布在（1±0.15）×106cm-3，300±15 km 和50±12.5 km 的区间。电离层参数真值和反演结果对应的电子密度高度分布如图5（a）所示，135.6 nm 辐射强度观测值随观测视线切点高度的分布如图5（b）所示。图5 中的蓝线表示与各反演结果对应的电子密度（见图5a）和辐射强度（见图5b）的高度分布。绿线、红线分别对应反演结果均值与电离层真值。整体而言，噪声的存在使峰值高度以下的电子密度反演误差范围比峰值高度以上的误差范围大。一方面是由于临边扫描时，电离层从上往下，穿过的视线数逐渐减少，临边观测数据包含低电离层的信息比高电离层的信息少导致的；另一方面，由于峰值高度以下观测的辐射强度比350 km 以上的观测值高（见图5b），导致噪声也比350 km 以上的大。但反演结果均值与真值产生的电子密度分布几乎重合，只在峰值高度附近比真值约高1.44%（见图4a）。探测器的噪声计数使反演误差近似服从以0 为中心的正态分布，理想情况下，可在同一位置记录多次观测数据，通过求反演结果的均值来修正噪声计数引入的随机误差。但在实际观测中，同一位置只记录一次临边观测数据，这就需要通过提高仪器的信噪比来提高反演精度。

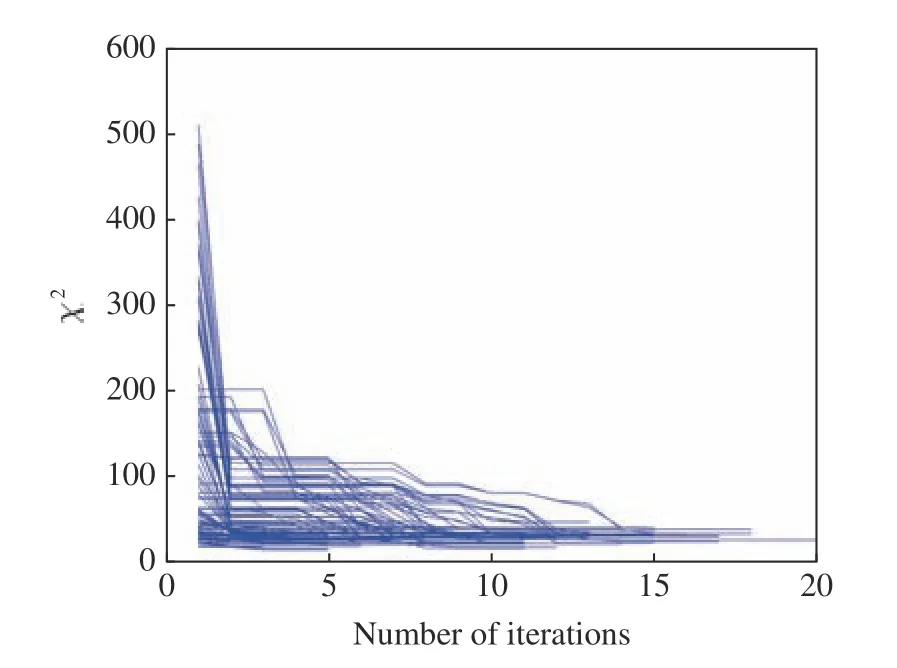
图3 χ2 随迭代步数的变化（不同曲线代表不同的反演，每次反演的迭代初值和噪声不同）Fig.3 Variation of χ2 with number of iterations(Different curve represents different inversion run.Each inversion run is different in both iteration initial value and added errors)

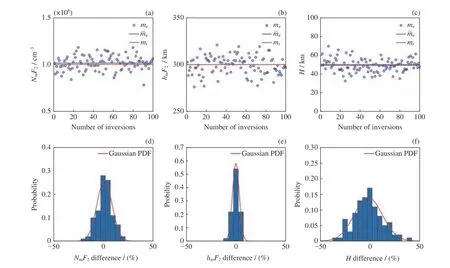
图4 100 次反演的结果分布及百分比误差的概率密度函数 (PDF)统计直方图（每次反演的迭代初值和噪声不同）Fig.4 Distributions of three ionospheric parameters with respect to true values and the Probability Density Function (PDF) histograms of percentage differences for 100 inversion runs (Each inversion run is different in both iteration initial value and added errors)

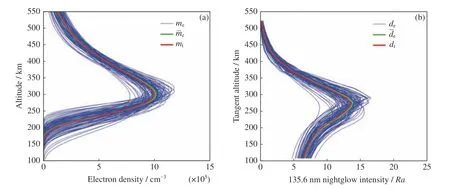
图5 100 次反演结果及反演结果均值与电离层参数真值对应的电子密度高度（a）和135.6 nm 辐射强度随视线切点高度分布（b）（每次反演的迭代初值与噪声不同)Fig.5 (a) Electron density altitude profiles and (b) 135.6 nm radiation intensity against tangent height of line of sight corresponding to the one hundred retrieved solutions,mean of solutions,true values of ionospheric parameters (Each inversion run is different in both iteration initial value and added errors)

3.3 仪器响应度

由于仪器灵敏度与积分时间因探测任务而异，这里将二者的乘积作为一个整体来评估对反演误差的影响。本文考察3 种情况的响应度，即0.1，1，10。对于每一种响应度，重复3.2 节的100 次仿真，计算NmF2与hmF2的反演值与真值的百分比误差，3 种响应度的反演误差分布如图6 所示。从图6 可以看出，误差点的散布范围随着响应度值的增加而朝着（0，0）点收缩变小，表明仪器响应度越高，反演误差越小。表1 列出了各个响应度情况下反演误差绝对值的最大值、最小值及均方根值。对于10 的响应度，NmF2在仿真中的反演误差优于5.19%，hmF2反演误差优于2.9%。整体来看，对于反演误差最大的情况（0.1），NmF2和hmF2的误差均方根分别为12.04%，7.89%。因此，适当的仪器响应度能获得精度较高的反演结果，这也为仪器的参数设计提供理论参考。

表1 3 种响应度情况的反演误差(%)数据对比Table 1 Comparison of the retrieved errors (%) of three responsivity cases

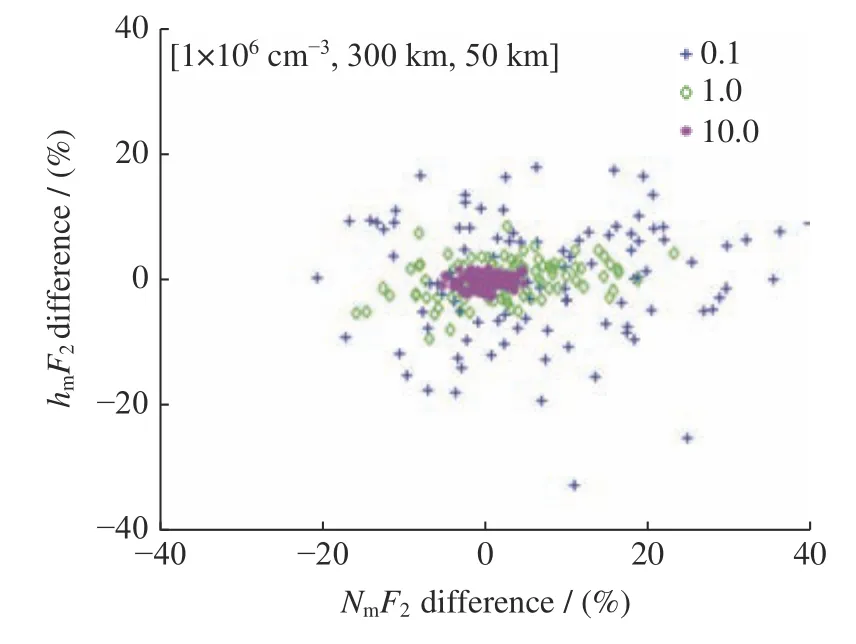
图6 三种仪器响应度情况下的NmF2和 hmF2 反演百分比误差对比Fig.6 Percentage difference of NmF2 and hmF2 for three responsivity levels

4 实测数据的反演

在验证了算法的可行性后，对GUVI 的实际临边观测数据进行反演。为覆盖不同的太阳活动条件、不同的地理位置和时间，选取2002 年7 月20 日和2007 年10 月4 日的夜间临边观测数据，太阳F10.7分别为190.7 和67.4，代表了太阳高年和太阳低年。图7所示的分别是2002 年7 月20 日和2007 年10 月4 日GUVI 临边观测反演结果的示例。红色“+”号表示GUVI L3 数据提供的离散的电子密度高度分布（EDP），每个时间地点的GUVI EDP 包含了23 个高度处的电子密度，23 个高度与本文划分的各层电离层中心高度一致。为了增加对比性，图中还添加了相同条件下的国际电离层模型IRI2016 的EDP 及基于IRI2016 仿真反演得到的EDP。GUVI 实测数据反演得到的EDP 虽然与IRI2016 模型存在差异，但在250km以上与GUVI数据的EDP的分布形状一致。另外，基于IRI2016 模型的仿真反演结果在200～450 km 几乎与IRI2016 的电子密度重合，能准确获得电离层的关键参数NmF2和hmF2；由于前向模型假设电子密度的高度分布符合Chapman 函数，实际的电子密度并非总是与Chapman 函数一致，特别是在峰值高度下方，这就导致200 km 以下存在较大的反演误差，在前向模型中准确表述电子密度真实的高度分布也是后续工作的重点之一。

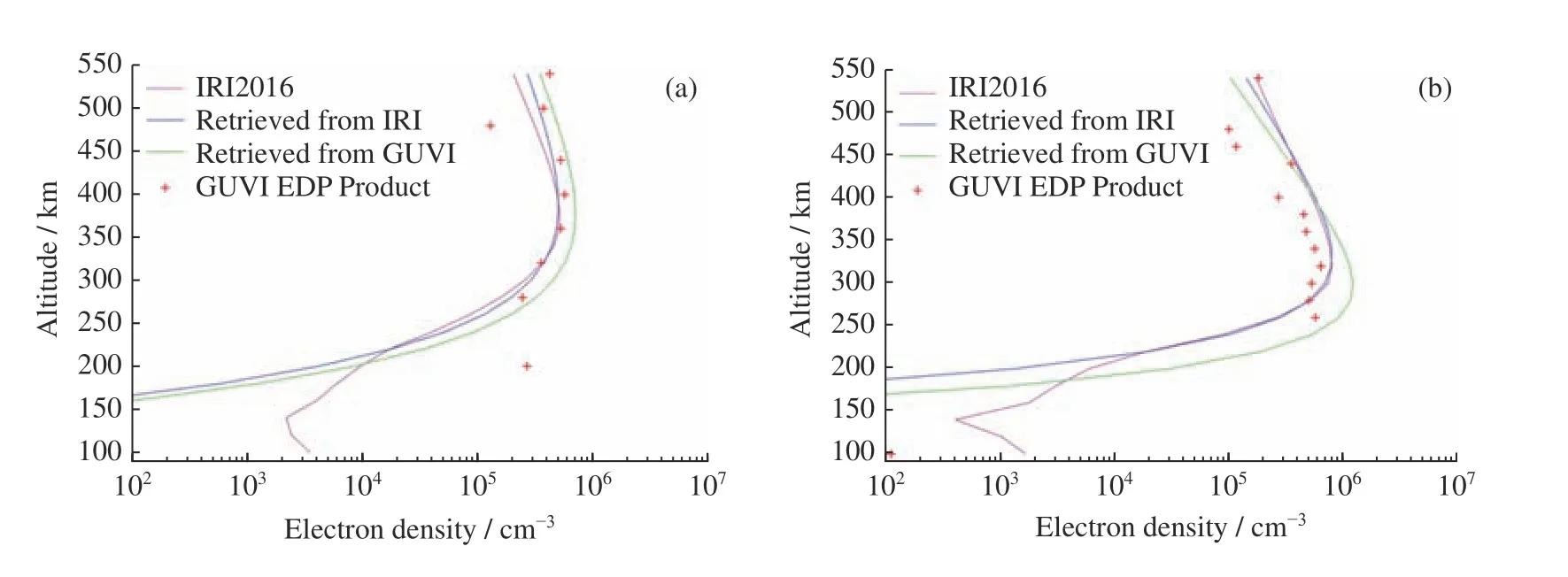
图7 2002 年7 月20 日（a）和2007 年10 月4 日（b）GUVI 135.6 nm 临边观测反演结果典型示例及与相同条件下IRI2016 模型与GUVI 数据的EDP 及基于IRI2016 模型仿真反演结果的对比Fig.7 Comparison among the typical inversion results from GUVI 135.6 nm observations,IRI2016 EDP,GUVI EDP product and the inversion results from simulated data based on IRI2016 model on 20 July 2002 (a)and 4 October 2007 (b) under the same condition

为评估电子峰值密度和峰值高度整体的反演精度，对反演获得的NmF2，hmF2与GUVI数据的NmF2，hmF2进行了比较分析。这里，GUVI 数据的NmF2和hmF2分别指GUVI EDP 中最大的电子密度及其对应的高度。图8（a）（b）给出了2002 年7 月20 日观测数据反演获得的NmF2，hmF2与GUVI 数据的NmF2，hmF2的线性拟合。2002 年属于太阳活动高年，不同地区在2002 年7 月20 日夜间的NmF2大概分布在0.3～2.3×106cm-3。在图8（a）中，NmF2数据点紧密聚集在拟合直线的两侧，只有少数几个离群点，NmF2的拟合直线斜率为1.12，表明被高估的NmF2更多。一方面除了3.2 节分析的仪器噪声带来的随机误差外，另一方面应是前向模型中忽略了产生少量135.6 nm 夜气辉的中和反应和共振散射过程带来的系统误差，这样相当于认为观测的辐射强度全来自O+与电子的辐射复合反应，会使电子密度被高估。在图8（b）中，夜间的hmF2主要在200～400 km。hmF2数据的拟合直线斜率为0.63，表明反演获得的大部分hmF2低于GUVI 数据的hmF2。一方面，产生135.6 nm 夜气辉的中和反应主要发生在峰值高度下方，对一些中和反应占比大（约10%）[11]的地方，忽略中和反应产生的135.6 nm 辐射可能会导致电离层峰值高度下移。另一方面，GUVI 数据提供的EDP 是离散的，相邻高度间距20 km，这使GUVI 数据本身的峰值高度的不确定度范围为±20 km。图8（c）（d）给出了2002 年7 月20 日观测数据反演得到的NmF2，hmF2与GUVI 数据的NmF2，hmF2之间百分比误差的概率密度分布，横轴被划分成40 个宽度为0.05 的子区间。NmF2百分比误差落在（10±2.5）%子区间的概率最大（13%），其中90%的NmF2百分比误差分布在（10±25）% 的范围，如图8（c）粉色区域所示。对于hmF2，百分比误差落在（0±2.5）%子区间的概率最大（25%），其中90% 的百分比误差分布在（0±15）% 的范围,如图8（d）粉色区域所示。虽然hmF2的线性拟合与直线y=x偏差较大，但百分比误差分布比NmF2的更窄更接近0。

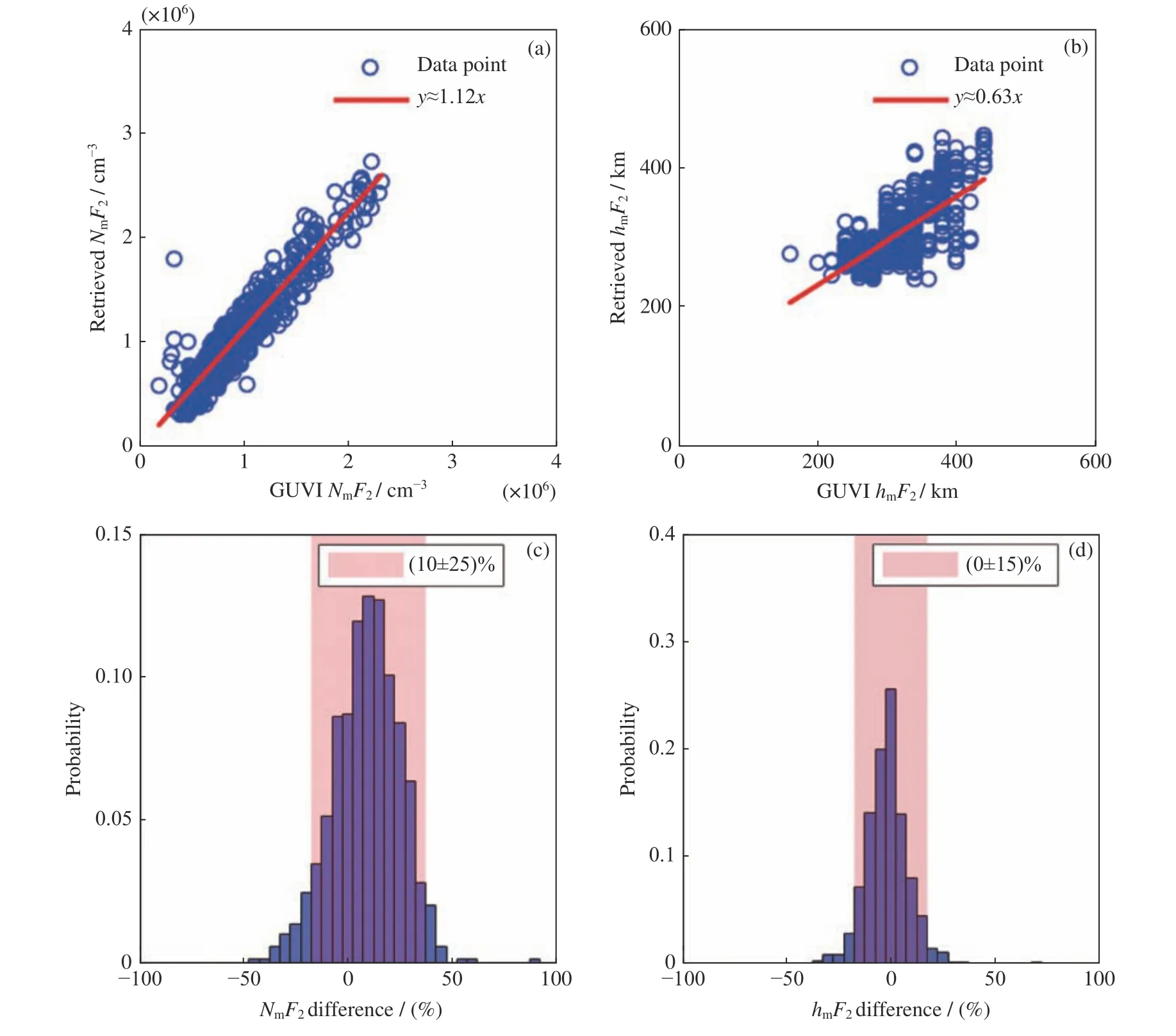
图8 2002 年7 月20 日的观测数据反演获得的电离层参数与GUVI 数据电离层参数的比较Fig.8 Comparison between retrieved ionospheric parameters from observations and GUVI data on 20 July 2002

图9（a）（b）给出了2007 年10 月4 日观测数据反演获得的NmF2，hmF2与GUVI 数据的NmF2，hmF2的线性拟合。2007 年属于太阳活动低年，不同地区在2007 年10 月4 日夜间的NmF2主要分布在0.1～1.5×106cm-3，明显低于太阳活动高年夜间的NmF2。2007 年10 月4 日的NmF2数据点同样密集分布在拟合直线的两侧，但离群点比2002 年7 月20 日的多且离群距离更远。NmF2的拟合直线斜率为1.08，表明多数反演得到的NmF2高于GUVI 数据的NmF2，原因与前述类似。在图9（b）中，hmF2数据的拟合直线斜率为0.61，同样表明反演获得的大部分hmF2低于GUVI 数据的hmF2，原因与前述类似。图9（c）（d）给出了2007 年10 月4 日观测数据反演得到的NmF2，hmF2与GUVI 数据的NmF2，hmF2之间百分比误差的概率密度分布，横轴被划分成40 个宽度为0.05 的子区间。NmF2百分比误差分布在（5±2.5）%子区间的概率最大（10%），其中90%的NmF2百分比误差分布在（5±40）%的范围，如图9（c）粉色区域所示，表明2007 年10 月4 日的NmF2误差比2002 年7 月20 日的分布更广。相反地，2007 年10 月4日hmF2百分比误差比2002 年7 月20 日的分布更集中，约1/3 的误差落在了（-5±2.5）%的子区间，有94%的百分比误差分布在（-5±15）% 的范围，如图9（d）粉色区域所示。

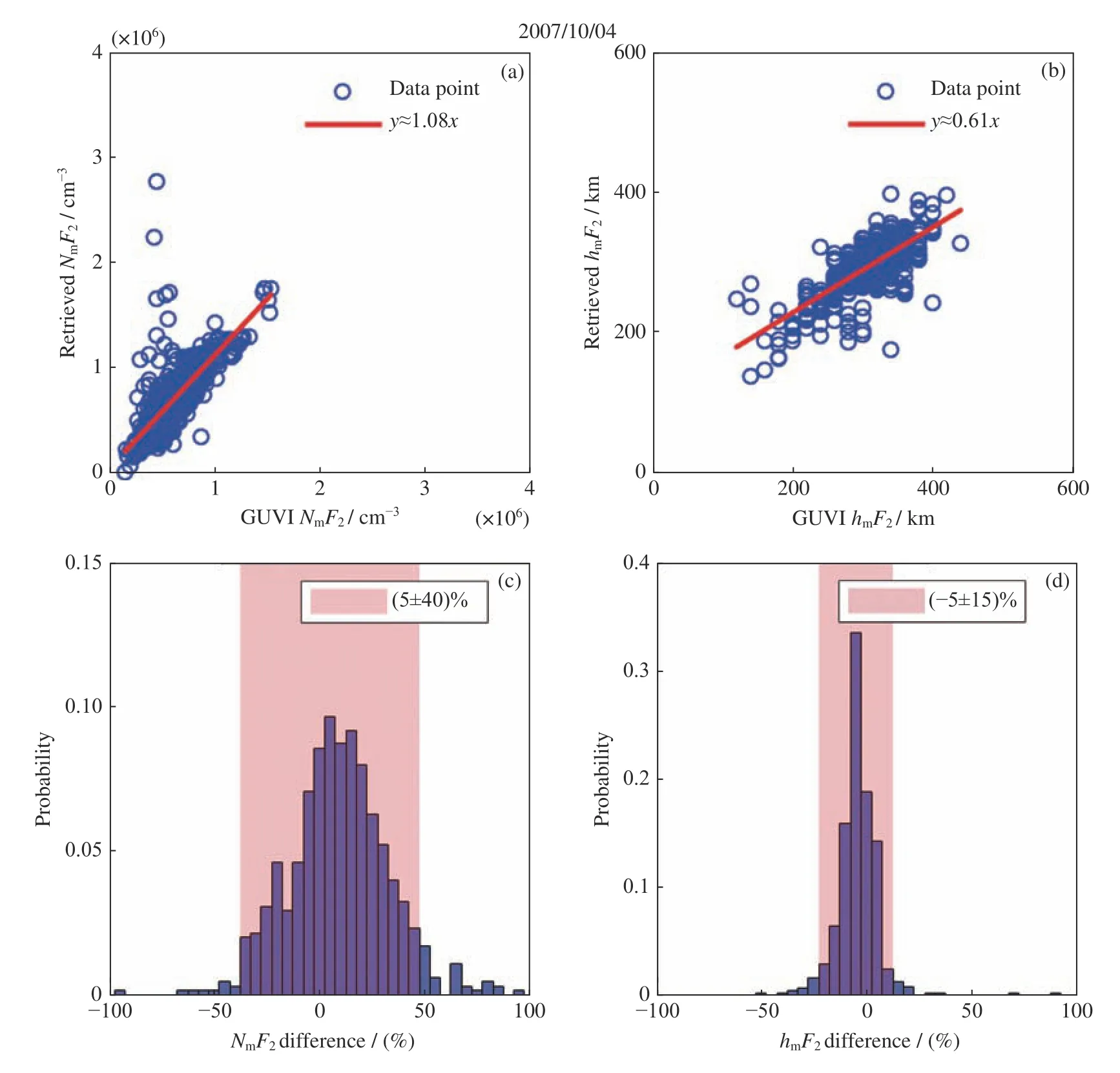
图9 2007 年10 月4 日的观测数据反演获得的电离层参数与GUVI 数据电离层参数的比较Fig.9 Comparison between retrieved ionospheric parameters from observations and GUVI data on 4 October 2007

通过对比分析实测数据反演获得的电离层参数与GUVI 数据，发现建立的135.6 nm 夜气辉辐射模型有高估电子峰值密度和低估峰值高度的趋势。对于实测数据，反演误差主要包含仪器噪声计数带来的随机误差和反演模型带来的系统误差。当反演模型精确时，随机误差的概率密度分布近似以0 为中心的正态分布，如图4 所示。系统误差主要来自135.6 nm夜气辉辐射观测模型，包括忽略峰值高度以下的中和反应、Chapman 电子密度分布假设、离散的电离层划分。系统误差体现在随机误差概率密度分布的平移上，例如2002 年7 月20 日的NmF2误差分布右移到以10%为中心；2007 年10 月4 日的NmF2误差分布以5% 为中心，hmF2误差分布以-5% 为中心。从误差百分比的概率密度分布看，NmF2误差分布比hmF2误差分布广，说明反演的NmF2与GUVINmF2的差值范围更大。从离群点和误差分布范围看，2002年7 月20日NmF2的反演精度优于2007 年10 月4 日，表明反演精度与观测到的辐射强度大小有关，辐射强度越大或电子密度越高，整体反演误差就越小。

5 结论

基于原子氧135.6 nm 夜气辉辐射强度与电离层电子密度的关系，建立了一种应用于星载远紫外光谱仪临边观测电离层反演电子密度的反演算法。本文通过仿真验证了该算法的可行性，仿真结果如下。

（1）对于同一组临边观测值，算法与迭代初值无关，能收敛到唯一的最大似然估计解。

（2）对仿真而言，反演模型是精确的，仪器噪声产生的随机误差概率密度分布近似以0 为中心的正态分布，探测器在短时间内对同一地点进行多次观测，求反演均值可修正噪声带来的随机误差。

（3）反演误差与仪器响应度的选择有关，仪器响应度越大，电离层参数的反演误差越小，可为仪器的响应度设计提供参考。

对不同太阳活动强度、不同时间地点的GUVI 临边实测数据进行反演，获得了电子密度高度分布。通过与GUVI 数据的电离层参数（NmF2，hmF2）进行比较分析可知，本文建立的135.6 nm 夜气辉辐射观测模型会高估NmF2，同时低估hmF2。太阳活动高年（2002 年）实测数据反演得到的NmF2被整体高估了10%左右；虽然hmF2误差落在（0±2.5）%子区间的概率最大，但反演得到的hmF2大部分低于GUVIhmF2。太阳活动低年（2007 年）实测数据反演得到的NmF2被整体高估了5% 左右，且误差分布更广；hmF2被整体低估了5%左右。

后续的工作重点主要是进一步提高反演精度，优化135.6 nm 夜气辉辐射观测模型，例如将产生少量135.6 nm 辐射的中和反应和辐射传输效应纳入辐射强度的计算中，并寻求精确的电子密度高度分布的数学表述。

致谢GUVI 观察数据由NASA MO&DA 项目免费提供（数据来自http://guvitimed.jhuapl.edu/data_products）。GUVI 探测器由Aerospace Corporation 和Johns Hopkins University 设计及建造。