基于极大验后推估理论的全球电离层地图预报*

刘昂 王宁波 李子申 张研 李昂

1(中国科学院空天信息创新研究院 北京 100094)

2(中国科学院大学电子电气与通信工程学院 北京 100049)

0 引言

全球卫星导航系统（Global Navigation Satellite Systems，GNSS）精密定位技术日趋成熟并得到广泛应用，对于高精度实时定位的需求日益迫切[1]。随着导航卫星载荷（星载原子钟等）质量的不断提升以及卫星轨道、钟差等精密改正信息精度的不断提高，地球电离层对GNSS 信号产生的延迟误差已成为影响卫星导航高精度定位精度的主要误差源之一[2]。为满足卫星导航高精度位置服务需求，国际GNSS 服务组织（IGS）2017 年起实施了全球实时电离层实验项目。受限于实时GNSS 测站的数量与分布，GNSS 实时电离层观测信息主要集中于陆地区域且分布不均匀；实际应用中，GNSS 实时数据流并不十分稳定且存在数据流中断的情况，严重制约了实时全球电离层的建模精度与可靠性。针对此，中国科学院（CAS）电离层分析中心和西班牙加泰罗尼亚理工大学（UPC）分别提出了基于“预报+实测”与“压缩传感”的实时全球电离层建模方法[3,4]，其核心是引入不同的预报电离层信息作为先验电离层约束，实现实时全球电离层模型的稳定解算。可以看出，电离层预报GIM 不仅可用于不同时间尺度电离层信息的预测，还可辅助进行实时电离层GIM 的可靠计算。实现电离层信息的精确预报具有重要研究意义。

从预报方法上看，全球电离层总电子含量（TEC）预报方法可分为直接法和间接法[5]。直接法基于事后全球电离层地图（GIM）的历史格网点TEC 数据构建模型，逐格网点进行电离层TEC 预报；间接法则基于全球电离层TEC 函数模型（例如球谐函数或B 样条函数等），构建电离层系数对应的预报模型，进而利用预报的模型系数重新构建电离层模型，实现全球电离层TEC 的预报。从数学模型分析，电离层TEC 预报方法一般包括滑动平均自回归法[6,7]、最小二乘配置法[8,9]、神经网络[10-12]等。滑动平均自回归法是统计学中对宽平稳时间序列的建模方法，其在对TEC 建模时需要先采用最小二乘等方法扣除趋势项，进而将残差视为宽平稳随机信号进行模型的构建。最小二乘配置法是广义测量平差中的基本平差方法，该方法在考虑电离层TEC 趋势项的同时引入随机项参数，实现对TEC 趋势项和随机项的同步外推。神经网络方法能够较好地拟合非平稳时间序列中隐含的非线性关系，基于该方法对电离层TEC 的预报效果较好[12]，但是神经网络模型的物理意义并不明确，如著名的“黑匣子”问题[18]。

能够提供全球电离层预报GIM 的IGS 电离层分析中心有欧洲定轨中心（CODE）、欧洲空间局（ESA）和UPC[13]。目前，UPC 仅提供2 天的预报GIM，CODE 与ESA 提供1，2 天的预报GIM。UPC 预报GIM 基于直接法实现，首先对GIM 进行离散余弦变换提取频域主成分，进而基于自回归理论对每个频域分量进行预测，最后利用离散余弦逆变换实现预报GIM 的重构[14]；CODE 预报GIM 基于间接法实现，利用最小二乘配置理论实现球谐模型系数的预测外推[15]；ESA 预报GIM 的处理策略目前尚未公开。

中国科学院空天信息创新研究院联合精密测量科学与技术创新研究院，筹建了亚太地区首家IGS 电离层分析中心，代表中国科学院向全球用户提供高精度电离层科学数据服务。CAS 例行提供实时、快速与最终GIM，其中，实时GIM 每60 s 播发一次，精度为1.5～3.0 TECU（1 TECU对应GPS L1频率上16.2 cm 的伪距延迟），快速GIM 延迟1～2 天发布，最终GIM 延迟5 天发布，事后GIM 精度与CODE及UPC 等相当，实时GIM 与事后GIM 相比精度低1.7%～4.9%[16-19]。为丰富CAS 分析中心电离层GIM 并服务于CAS 实时电离层GIM 的例行稳定解算，本文提出基于极大验后推估理论的全球电离层预报方法。以CAS 快速电离层GIM 为基础，通过功率谱分析提取各阶球谐系数的变化周期，将球谐系数的主周期项纳入趋势函数进行拟合，进而基于极大验后推估的方法预报趋势项未拟合的宽平稳信号，实现1 天、2 天和5 天全球电离层TEC 的预报。

1 极大验后推估电离层TEC预报模型

CAS 快速GIM 基于15 阶球谐函数实现全球电离层TEC 模型的构建，同时采用广义三角级数逐基准站实现局域电离层TEC 模型的构建，结合球谐函数全球覆盖和广义三角级数区域高精度的优势，基于站际分区法逐个格网点计算电离层TEC，进而生成IONEX 格式的电离层TEC 格网[20]。本文以CAS 快速GIM 对应的球谐系数序列作为输入，开展全球电离层TEC 预报。

各阶球谐系数不仅具有明确的物理含义（例如零阶系数表征全球电离层TEC 的平均值），还表现出较强的周期性变化规律。通过对各阶球谐系数时间序列进行功率谱分析，可以获得各阶球谐系数对应的周期项。为准确表征球谐系数中周期项的变化，同时准确描述随机变化项的特征，本文提出了基于极大验后推估模型的球谐系数预测方法，并基于预测球谐系数实现了全球电离层TEC 的预报。

1.1 极大验后推估模型

传统的最小二乘法预报电离层TEC，未考虑TEC 序列中包含的随机项参数，即未考虑TEC 残差中具有统计意义的宽平稳信号。白噪声与随机项参数的区别在于白噪声信号在不同时刻互不相关，而随机项参数之间具有时间相关性。因此，本文在TEC时间序列预测研究中，通过分析TEC 历史数据中随机项参数的统计规律，进而采用极大验后推估模型，实现对未来时刻随机项参数的预测。球谐系数序列可写为如下同时包含傅里叶级数描述的趋势项与随机项参数的形式：

式中，Cmn(t)表示m度n阶球谐系数值，t表示球谐系数值对应的时刻，ai和bi表示傅里叶级数对应的待估参数，K表示预先选定的球谐系数周期数，fi表示各周期项对应的频率（由1.2 节功率谱估计得到），S表示球谐系数未拟合参数，N表示随机白噪声向量。

最小二乘配置理论中，将球谐系数未拟合参数残差与高斯白噪声同等看待，使得球谐系数未拟合参数的取值拟合于期望，损害了推估的质量。这里球谐系数未拟合参数的求解参照文献[21]的“拟合推估新解之--两步解法”，能够更准确地推估球谐系数未拟合参数，即

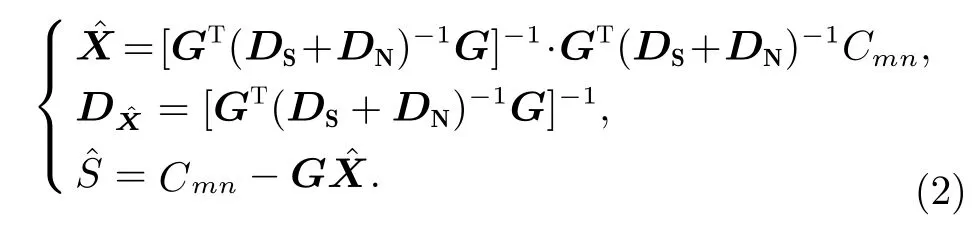
基于极大验后估计准则，计算得到球谐系数未拟合参数的预报值为

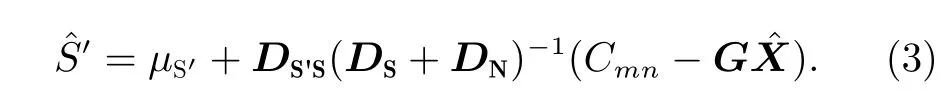
1.2 功率谱估计

球谐系数趋势项的拟合基于傅里叶级数开展，通常提取傅里叶级数周期的策略是，对时间域观测数据作傅里叶变换到频率域，考虑到球谐系数时间序列具有周期振荡的特性，球谐系数在时间域并非绝对可积，这违背了傅里叶变换的正则条件。为此，引入功率谱估计作为提取傅里叶级数周期的方法[22]。离散随机信号的功率谱定义为

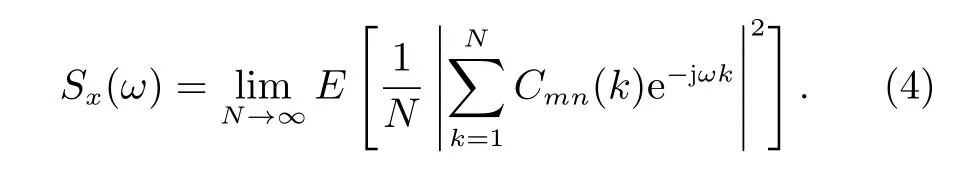
式中，Sx(ω)表 示球谐系数的功率谱，ω表示角频率，E表示期望算子，j 表示虚数单位，N表示观测值时间序列总数。

实际上不存在数量无穷的球谐系数时间序列，通常采用周期图[24]作为功率谱密度的实际估值公式，即

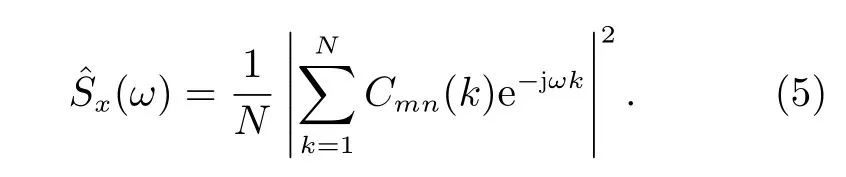
需要说明的是，周期图对功率谱的振幅估计是有偏估计。数据量越大振幅估计越准确，但振幅的方差并不随数据量的增大而减小；需要折中考虑准确度与精确度，选取合适的数据长度。本文采用将球谐系数序列拆分为多份并分别进行功率谱估计后取平均的策略，以减小周期图的方差。图1 给出了零阶球谐系数时间序列以及应用周期图法的功率谱分析结果。

图1 电离层零阶球谐系数时间序列及其功率谱分析Fig.1 Zero-order spherical harmonic coefficient time series and its spectrum analysis diagram

1.3 自协方差估计

以拟合后的残差计算球谐系数未拟合参数的协方差值，有

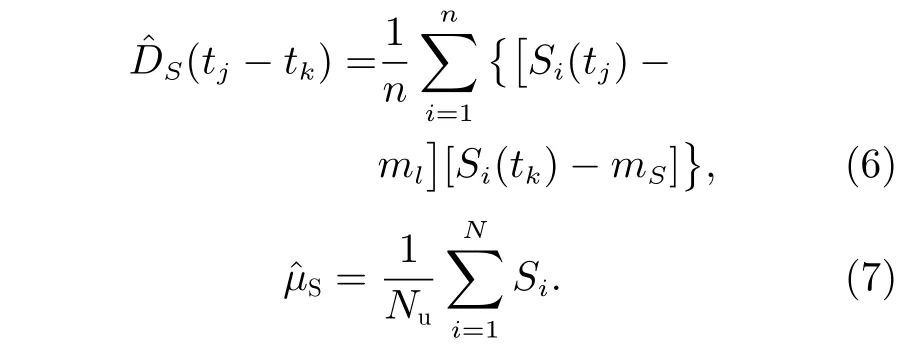
球谐系数拟合残差中不仅包含球谐系数未拟合参数，还包括随机白噪声的影响，计算得到的自协方差曲线是关于自变量时间间隔的一系列散点。这里采用多项式函数拟合自协方差值的离散点，得到自协方差函数，进而处理得到式（2）和式（3）中未拟合参数的先验协方差阵。

1.4 球谐函数预报

将预测的各阶球谐系数代入式(9)的球谐函数，即可实现全球电离层TEC 预报，即

基于极大验后推估算法预报全球电离层TEC 的流程如下。

步骤1通过功率谱估计方法确定各阶球谐系数对应的趋势项周期。

步骤2基于最小二乘法实现球谐系数趋势项拟合并获得各球谐系数的拟合残差序列。

原来老周也是一位诗人。我们就这样熟悉了，周末也常常一同下乡采风。有一次，我们在乡下遇到了老马。老马炒了几个菜，在露天的稻床上，我们兴奋地喝起酒来。他们谈论着稻草，谈论着稻草中的诗意。老马和老周谈得十分投机，相见恨晚，竟把我晾在一边。

步骤3利用球谐系数的拟合残差计算球谐系数未拟合参数的自协方差，并基于多项式计算得到的自协方差函数，构造球谐系数未拟合参数方差的协方差阵。

步骤4基于极大验后推估法得到球谐系数未拟合参数，对球谐系数未拟合参数进行时间外推，利用球谐系数趋势项与球谐系数未拟合参数构造球谐系数预报模型，实现球谐系数的预报。

步骤5利用预报的球谐系数及球谐函数，实现全球电离层TEC 的预报以及提前1 天、2 天、5 天预报GIM 的生成。

2 CAS 预报GIM 精度分析

2.1 评估方法

采用7 天CAS 快速GIM 对全球电离层TEC 进行1 天和2 天的预报，采用21 天CAS 快速GIM 进行5 天的预报。CAS 快速GIM 时间分辨率为1 h，每个时刻对应256 个球谐系数，时间延迟为1 天。为分析预报GIM 在全球不同地区的精度情况，分别以IGS 最终GIM、Jason-2 测高卫星电离层TEC 以及全球70 个IGS 基准站实测TEC 为参考，评估CAS预报1 天、2 天和5 天GIM 在全球海洋及陆地区域的实际精度。

IGS 最终GIM 由各电离层分析中心的最终GIM综合得到，能够准确描述全球电离层TEC 的分布情况[23]。Jason-2 海洋测高卫星TEC 可以评估GIM 预报GIM 在海洋地区的性能，评估时需要对预报的GIM 进行时间和空间域插值，得到测高卫星观测处的TEC 预报值[24]。基于IGS 基准站的TEC 评估采用绝对TEC 和相对TEC 两种方法评估，测站绝对TEC 由相位平滑伪距方法处理得到，相对TEC 由载波相位差分法处理得到[25]。

2.2 IGS-GIM VTEC 评估

利用 2015 年6 月29 日06:00:00 UTC 时刻CAS，CODE，ESA 和UPC 的电离层预报GIM（XXXP1和XXXP2 分别表示不同机构的预报1 天和预报2 天GIM，IGSG表示IGS最终GIM），由 于IGSGIM 的残差直观反映各分析机构预报GIM 在全球的残差分布。结果表明，CODP2 在全球大部分区域的残差不超过±5 TECU；ESAP2 在中国南部、印度以及印度洋北部等地区给出的TEC 偏低，在南海等地区给出TEC 偏高；CASP2 在太平洋和澳大利亚等地区给出的TEC 偏高；UPCP2 除在亚太地区给出的TEC 偏低之外，在全球大部分地区给出的TEC 均偏高，南半球高纬度地区较为明显。为分析不同预报GIM的残差特点，图2给出了2015年6 月29 日06:00 时不同预报GIM 以IGSG 为参考的全球残差频率分布直方图。总体而言，CODE，ESA，CAS，UPC预报2 天的GIM 在全球范围内的残差基本符合正态分布，但UPCP2 与IGS-GIM 相比存在显著偏差且STD 较大，这可能与UPC 分析中心采取的处理策略有关。

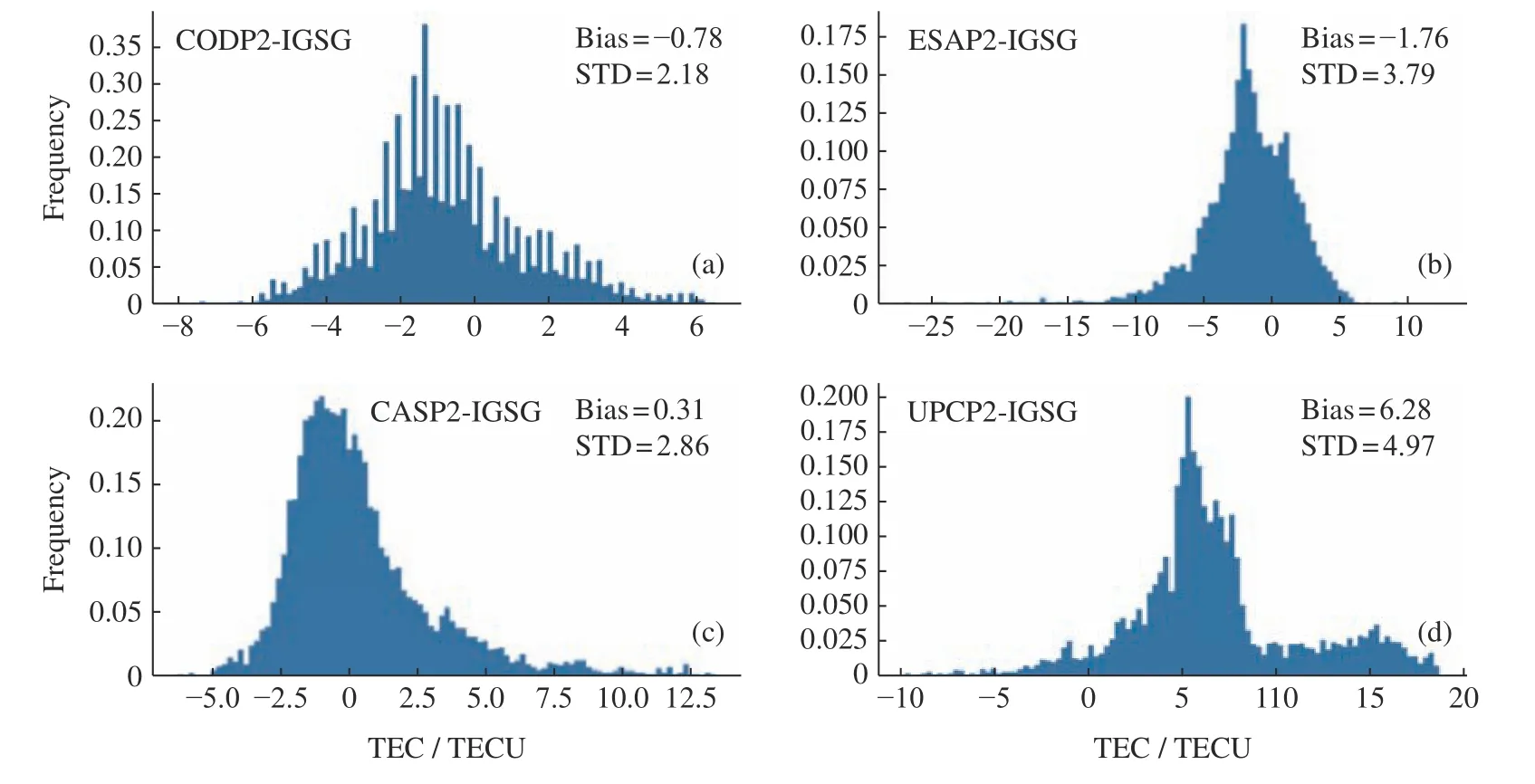
图2 不同预报GIM 与IGSG 相比电离层VTEC 残差频率分布的直方图（2015 年6 月29 日06:00:00 UTC）Fig.2 Ionospheric TEC residual histogram of different predicted GIMs compared to IGSG at 06:00:00 UTC on 29 June 2015

以IGS-GIM 为参考，评估2008 年第1 天至2017年第365 天各电离层分析中心预报的GIM 在全球范围内的总体精度情况。图3 给出了不同预报GIM 与IGS-GIM 相比的均方根误差时间序列。可以看出，各电离层分析中心预报GIM 与IGSG 之间的一致性与太阳活动水平之间存在较高相关性。CAS 与CODE预报GIM 之间的一致性较好，ESA 与UPC 的预报GIM 精度略差于CAS 与CODE。CAS，CODE，ESA和UPC 预报的GIM 均存在部分时刻RMS 较大的现象。考虑到电离层预报GIM 基于历史TEC 时间序列处理得到，其主要原因可以归为两方面：一是历史TEC 数据中包含突变值从而引起预报值的失真；二是实际TEC 数据受电离层扰动等异常效应的影响，预报GIM 难以反映TEC 的异常变化。

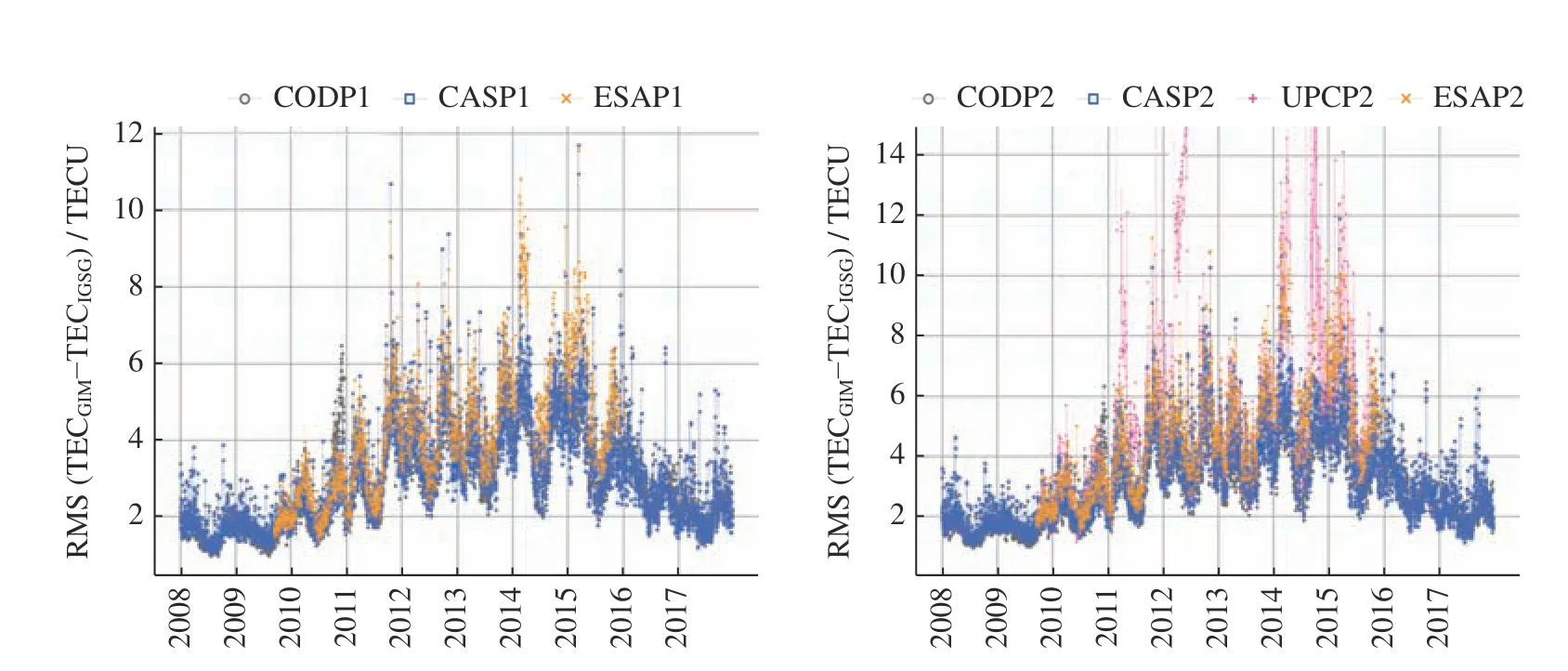
图3 2008-2017 年CAS，CODE，ESA，UPC 预报1 天和2 天GIM 的RMS 序列Fig.3 RMS series of CAS/CODE/ESA/UPC 1-and 2-day predicted GIMs compared to IGS-GIM during 2008-2017

表1 2008-2017 年CAS，CODE，ESA，UPC 预报1 天和2 天GIM 与IGS-GIM 相比的精度统计Table 1 Analysis result of CAS,CODE,ESA,UPC 1-and 2-day predicted GIMs compared with IGS-GIM from 2008 to 2017

2.3 Jason-2 VTEC 评估

以Jason-2 测高卫星数据反演的VTEC 观测为参考，评估不同GIM 预报GIM 在全球海洋区域内的应用精度。为避免测高卫星与GNSS 卫星轨道高度以及测高卫星硬件标定偏差引入的测高卫星TEC 观测量系统性偏差，在讨论分析时，以Jason-VTEC 与预报GIM-VTEC 之间的STD 为准，忽略Jason-VTEC 与GNSS-VTEC 之间系统性常数偏差的影响。以2015 年年积日（DOY）030～130 为例，图4 给出了Jason-2 VTEC 和各分析中心预报GIM 随地理纬度和地方时的变化，图5 给出了各分析中心预报GIM 与Jason-2 VTEC 相比的残差分布。从图4 和图5 可以清楚看出，CASP1，CODP2，CASP2，ESAP2，UPCP2给出的TEC分布与Jason-2TEC结果相近。ESAP2，UPCP2 预报的GIM 与Jason-2 VTEC相比残差相对较大。以Jason-2 VTEC 为参考的对比结果相比IGS-GIM 评估结果比较大，其原因一是Jason 卫星高度约为1300 km，而GNSS 卫星高度约为20000 km，导致Jason 卫星VTEC 实测值与GIMVTEC 之间存在着系统性偏差；二是Jason 卫星电离层观测位于海洋区域，而GIM 主要基于陆地区域的GNSS 数据计算得到，因而预报GIM 在海洋区域的应用精度相对较差。图5 中存在较多负值，即GIMVTEC 预报值低于Jason-VTEC 实测值的情况。其可能的原因一是Jason 卫星硬件延迟标定误差引起Jason-VTEC 实测值存在系统性偏差，二是当前基于单薄层假说计算得到的GIM 自身存在模型误差，特别是在高纬度地区[26]。

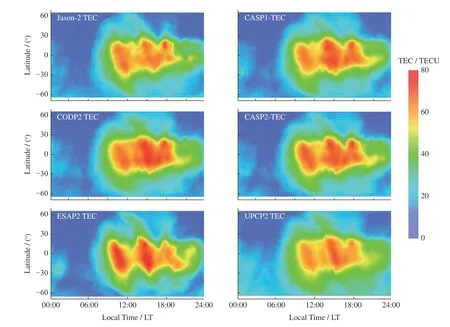
图4 不同预报GIM 随地理纬度和地方时的分布Fig.4 Global VTEC map in geographic latitude and local time coordinates

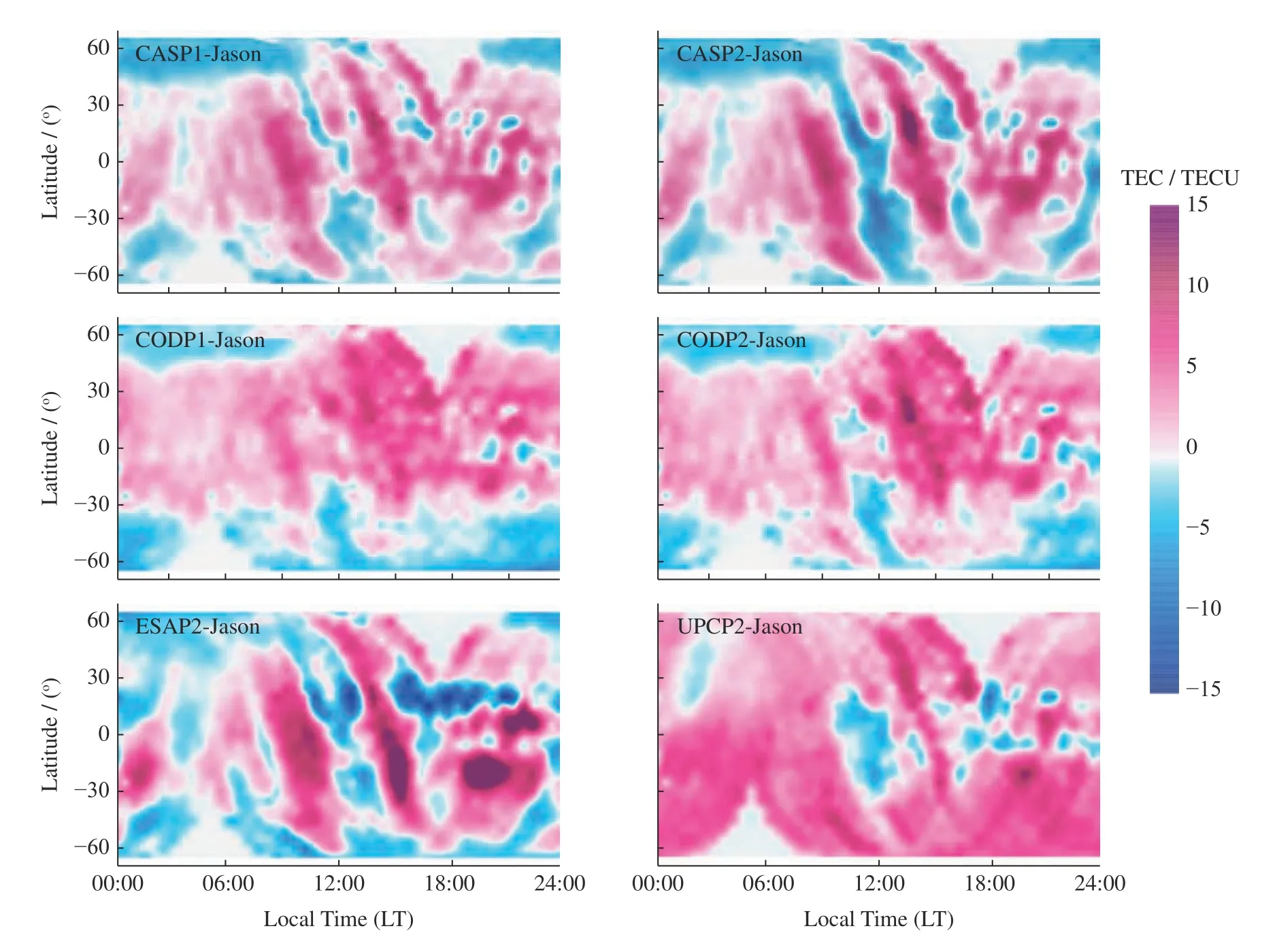
图5 不同预报GIM 与Jason-2 VTEC 相比残差随地理纬度和地方时的分布Fig.5 Different predicted GIMs difference map in geographic latitude and Local Time (LT)coordinates compared to Jason-2 VTEC

图6 给出了2008 年至2017 年不同预报GIM 与Jason-2 VTEC 相比的偏差和标准差序列。图6（a）显示，各分析中心预报的GIM 与Jason-2 VTEC 相比，均存在着一定系统偏差。图6（b）显示，不同分析中心预报GIM 的标准差在太阳活动程度低的年份普遍小于5.0 TECU;在太阳活跃程度高的年份，各分析中心预报GIM 的标准差普遍变大。总体而言，电离层TEC 预报GIM 的精度与太阳活动水平呈现较强的相关性。表2 中列出了评估期间CAS，CODE，ESA 及UPC 预报GIM 与Jason-2 TEC 相比的总体精度统计情况。CASP1 预报GIM 精度比CODP1和ESAP1 高0.5% 与2.5%，CASP2预报GIM 比ESAP2 和UPCP2 高3.2% 与2.1%；CAS 预报5 天GIM 的误差较大，这是因为随着外推时间增长，电离层趋势发生变化，准确预测难度增加，而球谐系数未拟合参数也由于时间间隔过长而降相关，使得预测的球谐系数未拟合参数时间相关性变弱。

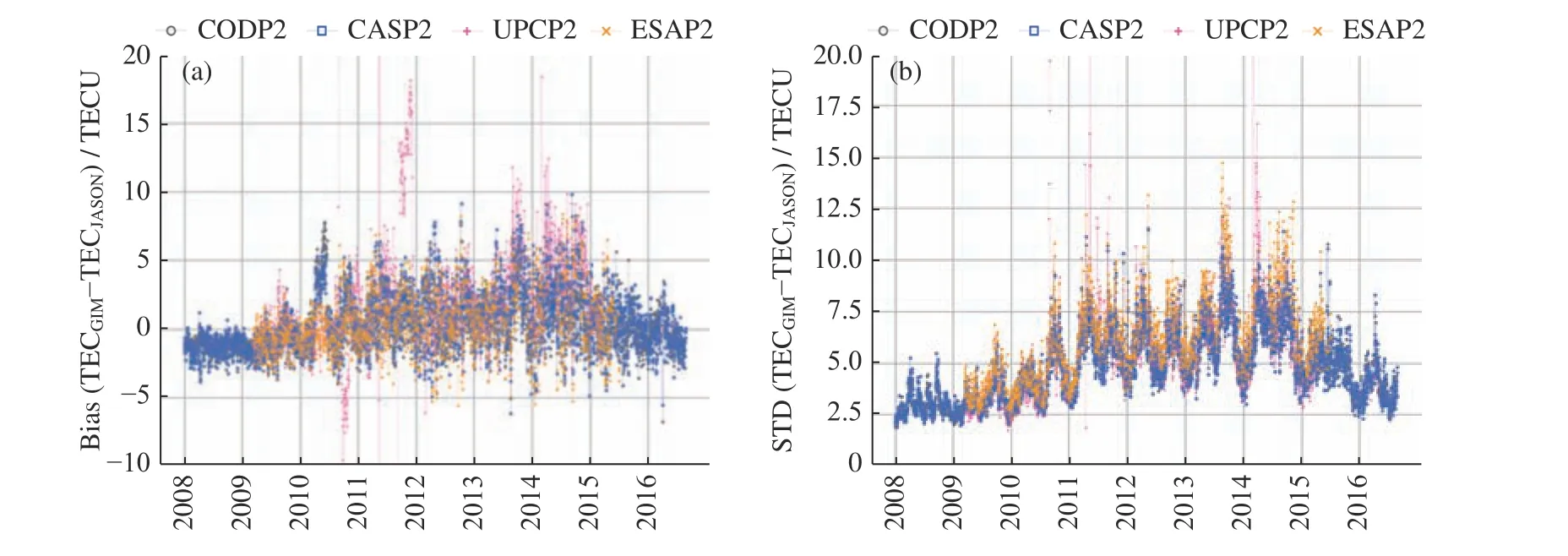
图6 不同预报GIM 与Jason-2 TEC 相比的Bias（a）和 STD（b）随时间的变化Fig.6 Different predicted GIMs bias (a) and STD (b) with time compared to Jason-2 TEC

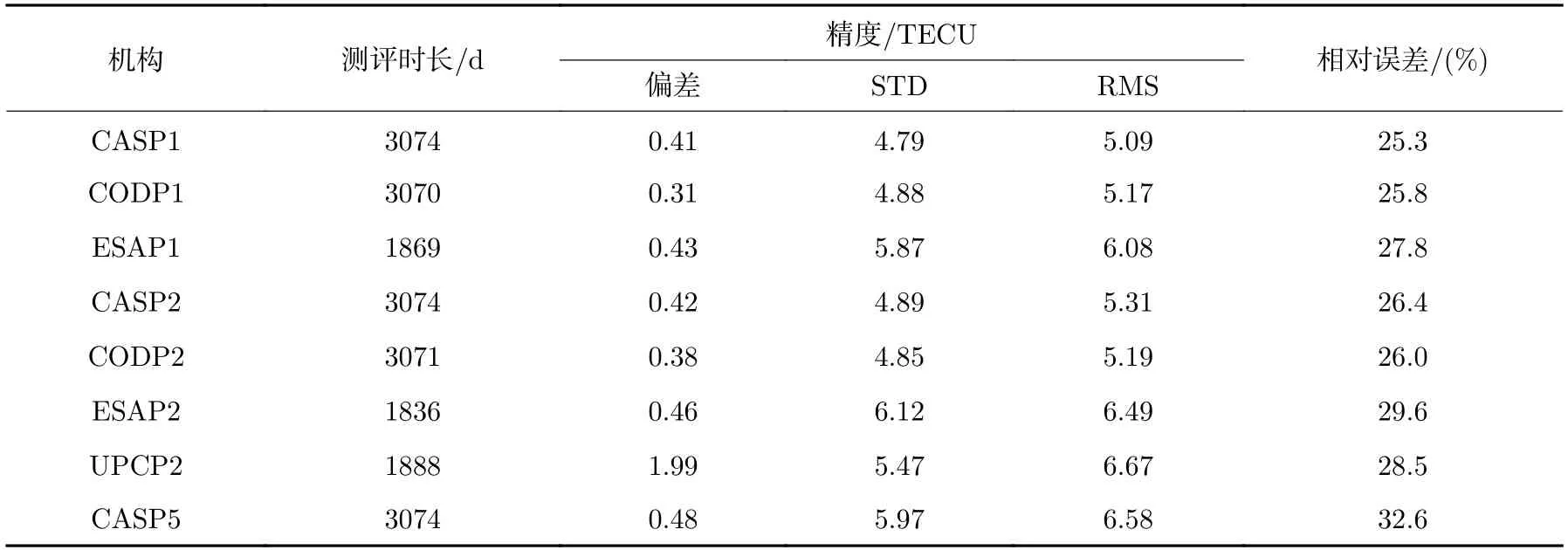
表2 2008-2016 年CAS，CODE，ESA 及UPC 预报GIM 与Jason-2 TEC 相比的精度统计Table 2 Analysis result of CAS,CODE,ESA and UPC predicted GIMs compared with Jason-2 TECs during 2008-2016

2.4 基准站GPS TEC 评估

为分析太阳地磁活动对电离层预报GIM 精度的影响，以高、中、低纬度地区6 个测站为例，分析2017 年9 月发生的太阳耀斑对电离层预报GIM 精度的影响。图7 给出了9 月7-9 日各测站GPS TEC与预报GIM 内插TEC 序列的对比情况，所选用的测站及其坐标如子图左上角所示，图7 中CASG 表示CAS 最终GIM。可以看出，在太阳活动平静时期，各测站的预报TEC 与GPS 实测TEC 之间一致性较好；但随着电离层扰动效应的发生，测站上空的TEC 预报值与实测TEC 值产生较大偏差。比较而言，事后GIM 的计算由于采用了较多的全球GNSS测站实测数据，能够准确反映测站电离层TEC 的变化。

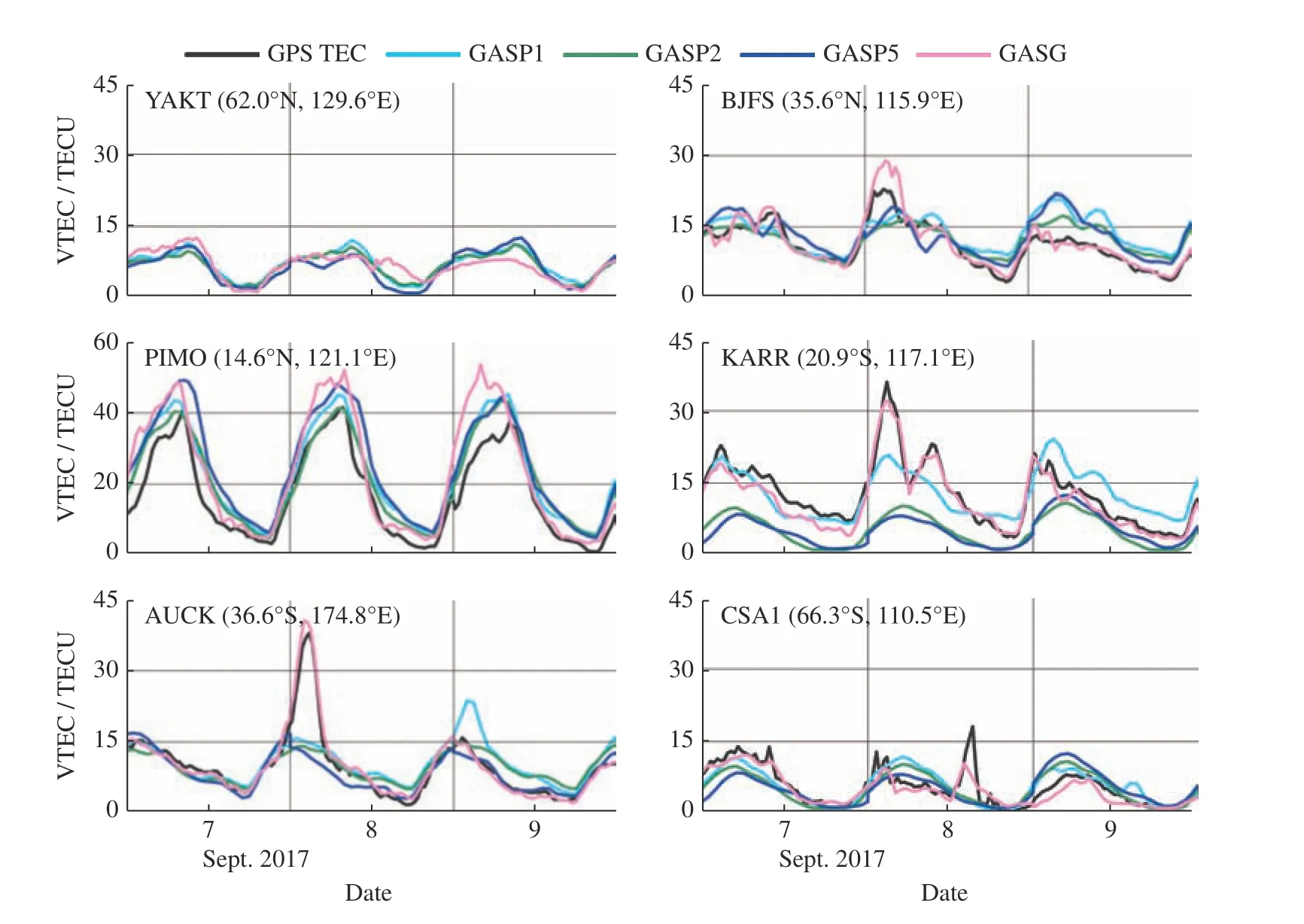
图7 预报的GIM-TEC 与实测的测站上空TEC 对比Fig.7 Comparison between the predicted GIM-TEC and the measured TEC over the station

为进一步评估预报GIM 在全球的精度情况，选取全球均匀分布的70 个IGS 基准站。表3 列出了预报GIM 与测站dSTEC 相比的误差统计结果。从偏差统计结果看，CODE 和CAS 分析中心的预报GIM没有明显系统性偏差，偏差值在0.20 TECU 以内。从均方根误差统计指标结果看，CASP1 和CASP2的GIM 精度与CODP1 和CODP2 相当，CAS 预报GIM 的平均RMS误差为2.58 TECU。CAS和CODE预报1 天和2 天的GIM 对电离层延迟的修正精度优于80%。

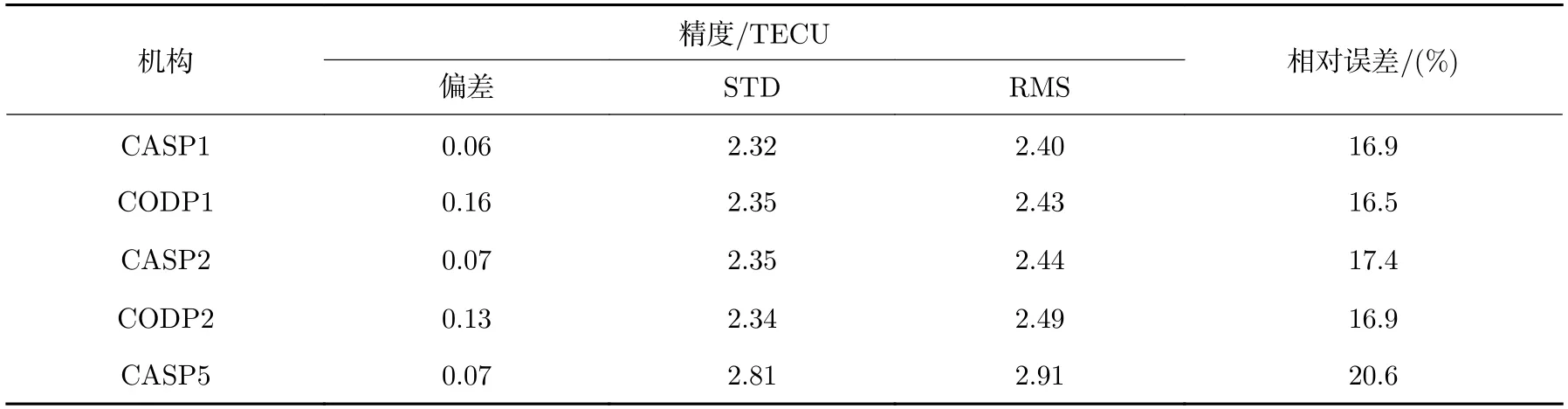
表3 CODE 与CAS 预报GIM 与实测的dSTEC 相比的精度统计Table 3 Analysis result of CODE and CAS predicted GIMs compared with GPS-dSTEC

3 结论

提出了基于极大验后推估理论的全球电离层TEC 预报方法。预报GIM 以CAS 快速GIM 对应的球谐系数序列为基础，首先基于功率谱估计方法对各球谐系数的时间序列周期项进行分析，再利用傅里叶三角级数拟合各阶球谐系数获得拟合残差，基于自协方差函数计算得到自协方差阵并预测球谐系数未拟合参数；在实现球谐系数预测基础上，最终生成CAS 预报1 天、2 天和5 天的GIM。

以IGS 最终GIM、Jason-2 测高卫星电离层TEC以及全球GNSS 基准站实测TEC 为参考，分析2008年至2017 年CAS 预报GIM 的精度统计情况。结果如下。

（1）与IGS-GIM 相比，CAS 预报1 天、2 天的GIM 的RMS 分别为3.06 和2.45 TECU，与CODE预报的GIM 精度相当，显著优于ESA 和UPC；

（2）与Jason-2 测高卫星TEC 相比，CAS 预报1 天的GIM 精度分别比CODE、ESA 预报GIM 高0.5%和2.5%，CAS 预报2 天GIM 精度分别比ESA和UPC 预报GIM 高 3.2%和2.1%，且太阳活动低年的预报效果显著优于太阳活动高年；

（3）与基准站GNSS TEC 相比,CAS 预报GIM的RMS 误差为2.40～2.91 TECU。基于极大验后推估理论的全球电离层预报方法，已用于CAS 电离层分析中心1 天、2 天、5 天预报GIM 的例行解算。