移动机器人智能车场停车资源调度分配
2023-01-14郑晓军郭星泽宁诗铎郑人豪史彦军
郑晓军, 郭星泽, 宁诗铎, 郑人豪, 史彦军
(1.大连交通大学机械工程学院, 大连 116028; 2.大连理工大学机械工程学院, 大连 116024)
“十四五”时期,推动高质量发展,构筑美好生活新图景,迫切需要新兴产业和技术的强力支撑,生活智能化、制造智能化成为社会的重要发展目标。截至2021年6月,中国汽车保有量已达3.84亿辆,“停车难”成为人们出行和汽车制造业存放车辆的新挑战。移动机器人(automated guided vehicle,AGV)智能停车场以其智能化程度高、占地面积小、存取车方便、降低停车者无效巡游时间等优势展示出强大的市场潜力,可广泛应用于如民航业停车场[1]、汽车制造企业的产品停放场区[2]以及大型商圈等对停放车辆有大量需求的场景。
在AGV的关键技术研究中,AGV的调度分配研究是主要难点和研究热点。目前,关于AGV的有关调度分配研究比较全面,但大多数以柔性制造系统和自动化码头为应用场景,中外学者对AGV系统的研究主要集中在路径规划、任务调度和冲突处理上[3];路径规划的研究有:文献[4]针对目前仓储AGV路径规划中存在的转弯次数多、冲突节点多的问题,对单AGV提出了一种基于障碍预测的改进A*算法;文献[5]提出了两阶段优化算法,首先根据AGV行驶规则生成初始路径,然后设计碰撞检测及避免算法对可能发生冲突的路径交叉点进行主动避撞调度。任务调度的文献有:文献[6]针对AGV的柔性作业车间调度问题,以最小化完工时间为目标,提出一种灰狼算法进行求解,有效平衡了算法的勘探能力和局部搜索能力;文献[7]对具有有限物流运输能力的智能车间AGV调度算法展开研究,为企业配置AGV小车及选择AGV调度规则提供一种有效的方法,保证了车间的生产效率;对于冲突处理的文献有:文献[8]针对实时动态环境下自动化分拣仓库中多AGV任务指派和路径规划的协同调度问题,以最小化加权总搬运完成时间为目标建立了混合整数线性规划模型,并提出一种集中与分散决策相结合的在线协同调度算法;文献[9]提出了一种基于停车等待、临时规避以及重新规划路径相结合的冲突解决策略,将冲突节点的路口数量、临时规避时间与重新规划路径所用的时间进行综合考虑。
上述学者均通过对AGV的调度分配与路径规划进行研究,提升了AGV的运输效率,但国内大多数研究对AGV运行情况的预测不足,大部分研究都是在冲突发生后进行协调,会造成AGV不必要的等待和停顿,对冲突预测问题考虑较少[10]。
在比较停车领域的AGV与物流、柔性制造车间等领域的AGV时发现:停车领域的AGV在任务规划时可以自由地选择目标停车位,故需着重研究停车资源的分配结果对AGV智能停车场运输效率的影响。基于以上研究,现针对大型商圈、民航业停车场在高峰时段以及汽车制造业停车场在生产制造后,要求同时、一次性大量的停车背景下,提出一种基于停车代价计算模型,通过对不同分配方案的停车代价进行计算,通过预测任务之间可能出现的路径干涉降低AGV在运输期间出现的冲突,并通过仿真验证合理分配停车资源,能够有效提升整个停车场的运输效率,从源头减少冲突的产生。
1 停车流程问题分析及环境建模
1.1 停车流程分析
AGV智能停车场的停车流程可分为3个部分:存取车请求、调度系统分配以及AGV系统运输,用户在发送停车请求后就可以离开,调度系统在生成任务时需要为车辆分配停车位资源与泊车AGV,然后对泊车路径进行规划,最后由AGV系统进行运输,如图1所示。本文研究主要集中在调度系统生成任务的停车位分配。
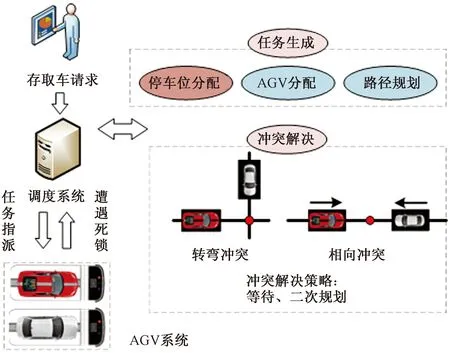
图1 停车系统示意图Fig.1 Parking system diagram
AGV智能停车场在高峰时段正常运转时,需要处理大量的任务请求,AGV系统需要不断将任务请求纳入到待执行任务队列;由于任务量巨大,一台AGV无法在规定时间内完成任务,一般需要多台AGV同时进行工作。但投入越多的停车AGV,会带来更高的成本与管理难题[11],系统也越容易陷入局部或全局死锁,造成AGV智能停车场的效率降低。
相较于柔性制造业车间、自动化码头等领域,经过改造后的停车场布局比较规整,规划出的路径比较单一,很难规划出多条路径;而为了提高停车场的最大增容率,一般将场内通道设置为双向单车道(同一时间、同一方向只能被一辆AGV占用),也增加路径之间的干涉,AGV在运输时更容易陷入冲突,造成不必要的等待和停顿:如图2所示,假设任务m1为存车任务将待停车辆从v1运输至目标停车位v2,任务m2为回程任务从v3至v1,任务m1的路径集合为{e1,e2,e3,e4},任务m2的路径集合为{e1,e2,e5},两个任务之间的干涉路径集合为{e1,e2},假设任务m1的优先级高于任务m2的优先级,那么任务m2的AGV必须等待任务m1的AGV完成干涉路径{e1,e2}后才能开始继续行进,造成了等待时间的浪费。
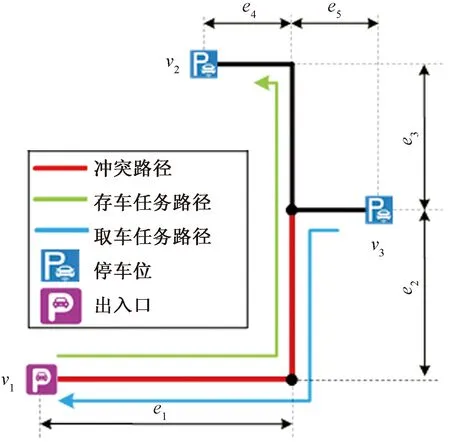
图2 停车场路径干涉Fig.2 Path interference diagram
若AGV系统在进行任务时,优先级低的任务未进行等待,开始了路径干涉部分的任务,则AGV之间就会陷入直线相向冲突死锁和转弯冲突死锁,如图 1所示,AGV需要将死锁信息传回调度系统,调度系统需要根据冲突解决策略安排某一任务进行等待或重新对任务路径二次规划,同样造成了时间和停车资源上的浪费,而引入的AGV数量越多,停车场内的等待和冲突产生的就会越多,造成的资源浪费越多,故通过合理规划停车任务的停车位,将相邻任务的停车位错开,可以合理减少相邻任务的路径干涉,提高停车场的运输效率。
1.2 环境建模
在现有的AGV路径规划研究中,已得到应用的环境建模方法有自由空间法、栅格法和拓扑地图法等。其中,栅格法的栅格具有信息量少、结构简单的特点[12-13],故栅格地图应用比较广泛;但粒度不容易界定,且建模效率不高,拓扑法的构造过程简单、存储小空间且计算效率高;基于典型停车场特征,本文采用拓扑法对停车场模型进行建模,该方法是将特殊位置的状态和位置信息抽象为节点形式,用有向线段连接相邻的节点,表征连通状态,形成点线相连的关系网,拓扑地图在搜索计算最短路径时的复杂程度取决于停车环境的可通行的节点的数量[14]。

图3 停车场拓扑模型Fig.3 Topological model of parking lot
本文研究的停车场的信息如表1所示。
根据所研究的问题,对停车场的通用假设参考文献[9],在此基础上,针对实际研究的停车场要求,本文研究提出了新的假设。
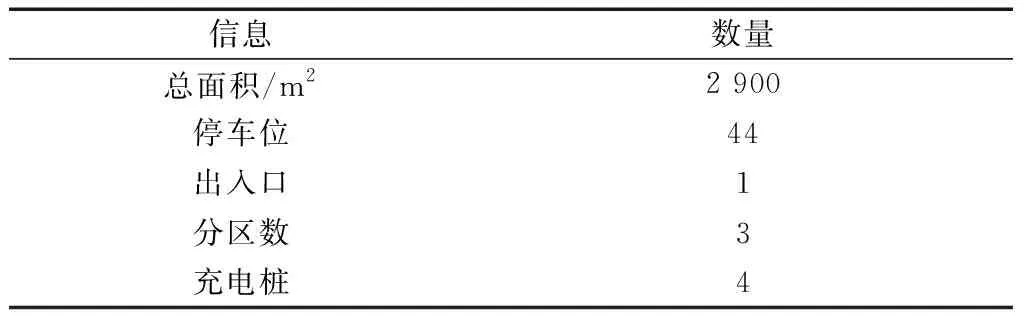
表1 改造停车场信息表Table 1 Modification of parking lot information
(1)在出入口一次只能有一辆AGV进行装车,需要等到载车的AGV进入停车场后才能进行下一辆车的装车。
(2)为防止停车场内赶超冲突,前一辆AGV进入停车场后,下一辆AGV需要等待10 s后进入停车场。
(3)在大型商圈、民航业停车场以及汽车制造业停车场在生产制造后,等待停入停车场的车辆数>停车内空余的停车位数量。
结合实际的AGV智能停车场环境及以上特征,将AGV智能停车场的现场物理环境抽象建立拓扑结构模型,绘制路口节点和各功能站点的连通图,如图3所示。
2 代价模型构建及资源分配算法
2.1 代价评价模型
智能停车场在接收调度任务后,需要根据停车位分配模型对停车位资源进行分配,在进行分配后,由停车AGV进行运输。在此基础上引入“代价”的概念,在调度系统将停车资源分配后,进行车辆停入停车位的代价计算,作为停车资源分配方案的评价指标,代价可以是不同的概念:死锁出现次数最小,停车时间最少等,也可以是不同指标的融合,停车代价的计算流程如图 4所示。当待停车辆发送停车请求时,一般会根据停车资源分配方法对待停车辆的车位进行分配;当为待停车辆分配车位后,需要利用本文提出的代价评价模型对车位分配的方案进行评价,最后根据评价出的代价选择最优的车位分配方案。

图4 停车代价计算流程Fig.4 Flow chart of parking cost calculation
本文研究提出了一种全新的智能停车场停车位分配方案的代价计算的概念,假设现有|I|辆待停车辆等待停入停车场,智能停车场内有|J|个空闲停车位,则智能停车场接收到的任务集合为M={I,J},M集合中的元素为mij,表示将当前待停车辆i停入停车位j。
本文模型建立的思想为将|M|个任务中,赋给每一个任务mij停车代价,在计算过程中,将每一辆待停车辆i停入空闲停车位j都会计算出停车代价cm,在整体规划出停车任务后,以整体的停车代价最小为目标函数。
目标函数为
(1)
式(1)中:z为完成停车任务后的代价之和;I为待停车辆集合;J为空闲停车位集合;Cm为任务m的停车代价。
本文模型将接受任务的停车代价最小为目标函数,约束为将可以停入停车场的待停车辆均停入停车场内,通过合理降低智能停车场的总体停车代价,提高智能停车场的吞吐效率。
代价函数可以随着研究的深入引入不同的概念,将其设置成总停车时长最小、AGV消耗电量最小,转弯次数最少、行驶路程最短、死锁次数最小等等不同的概念,也可以是不行概念的融合,将其设置的越精细,对AGV的运行预测的越准确,对提升停车场的效率效果越明显。
2.2 路径干涉概率模型
代价模型旨在预测AGV的运行情况,本文通过引入路径干涉概率的概念,通过计算停车资源分配方案的路径干涉概率,对AGV之间可能出现的冲突进行预测,通过减少AGV之前可能出现的冲突,降低等待时间和冲突的产生,提高停车场的运输效率。路径可以描述为图论问题[15],表示为r={V,E};对于每一个任务m,调度系统都会规划为其规划出一条路径,在得到任务m的路径Rm后,可以对任务m的总体路径进行计算,任务的m总路径长度为
(2)
式(2)中:lm为任务m规划出的路径Rm的总长度;Rm为任务的路径集合m;lr为任务某一段路径的长度。
本文引入的干涉概率表示为任务m在运输过程中可能与其他任务的路径干涉的概率。任务m与任务m′的中的路径是否干涉(pmm′)表示为
(3)
任务m与任务m′的中的干涉路径长度计算公式为
(4)
在得到任务m与任务m′的之间的干涉路径的长度后,任务m与任务m′的干涉概率(pmm′)计算公式为
(5)
在得到任务m与任务m′的干涉概率后,就可以整体对停车任务的干涉概率进行计算,计算公式为
(6)
式(6)中:cm为任务m的停车代价。
基于停车场干涉概率最小的计算公式为
(7)
2.3 停车资源分配方法
目前智能停车场常用的停车资源调度分配策略一般为随机分配(randomly allocate the parking lot to the pick-up point, RA)和优先分配距离取车点最近的停车位(first allocate the nearest parking lot to the pick-up point, FAN)两种方法[16]。本文在此基础上加入了交替分配按照距离取车点最近的停车位(alternately allocate the nearest parking lot to the pick-up point, AAN)和根据干涉概率整体规划分配停车位(according to the probability of interference to allocate the parking lot to the pick-up point, APIA)两种方法。AAN为根据停车点距离出入口的距离,按照一远一近交替将车辆停入停车场,APIA为按照冲突概率整体对停车资源进行规划。
一般为节省智能停车场内的资源消耗,会将待停车辆集中停放在同一区域以节省资源浪费,故本文将智能停车场划分为A、B、C三个区域,根据不同的待停车辆密度开放不同的区域。
假设目前停车场内没有车辆,待停车辆等待停入停车场,根据不同的待停车辆数量开放区域的方案如表2所示,分区结果如图3所示。

表2 不同停车数量开放区域表Table 2 Open area with different number of parking
3 算例分析与验证
3.1 计算及仿真结果
2.3节介绍了现存的两种停车资源分配方法RA与FAN,在此基础上提出了AAN与APIA两种方法。由于随机分配算法无法计算出稳定的结果,很难对计算结果进行量化分析以及与其他算法进行对比,故将其舍弃,着重对FAN、AAN、APIA 3种方法进行计算;FAN、AAN直接可以按照规则对其进行分配,并计算分配方案的累计冲突概率。而AIPA方法需要对停车资源按照目标函数进行全局规划,本文利用JAVA语言对停车方案进行编码,得到一个没有重复元素的排列编码,如图 5所示,将累计冲突概率设置为适应度函数,利用MOEA框架下的遗传算法进行整体规划,算法中的选择操作使用轮盘赌操作,算法中的交叉与变异算子均使用正常排列编码的单点交叉和基本位变异,得到的停车位分配顺序与累计冲突概率如表3所示。
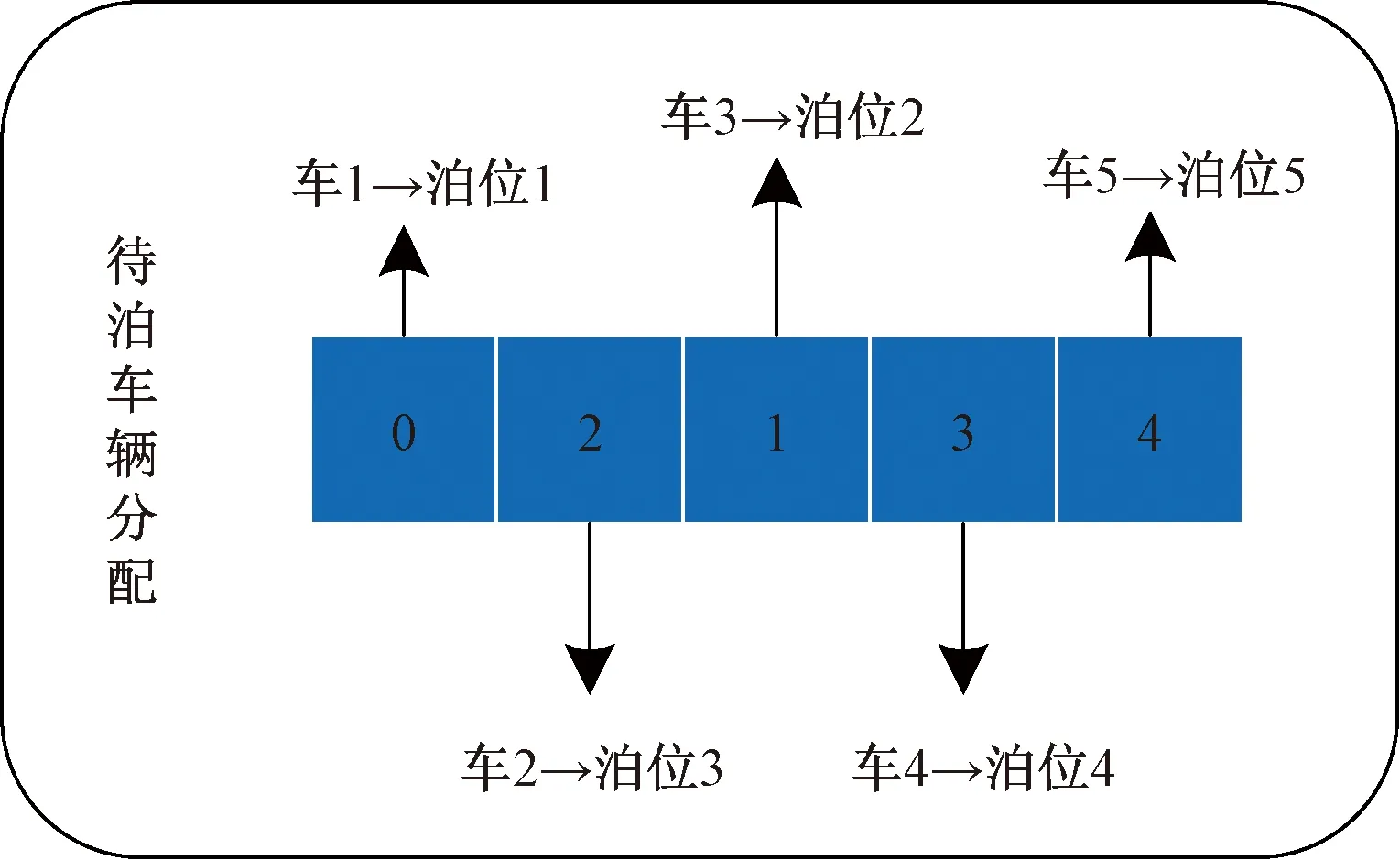
图5 解码示意图Fig.5 Decoding diagram
而累计干涉概率还是对AGV的运行情况进行预测,本文为证明减少任务之间的累计干涉概率对停车场运输效率的影响,利用Plant Simulation软件对停车场进行仿真:对不同AGV数量进行仿真,将所有停车任务均已完成且最后一辆AGV返回出入口的时间作为仿真总停车时长(total parking duration,TPD),将仿真总时长作为停车场运输效率的评价指标,并统计不同情况下的冲突等待次数(total waiting times,TWT)与总等待时间(total waiting duration,TWD),结果如表4所示。
3.2 结果分析
为了更直观地观察路径干涉概率数据,将路径干涉概率的数据绘制为折线图,如图 6所示,在不同方案下,路径之间的干涉概率呈下降趋势。从图6中可以看出,3种方案的下降趋势:方案3>方案2>方案1,在方案1中,开放区域的停车位数量较少,路径之间的干涉概率FAN>APIA>AAN,且干涉概率相差不大,故本文提出的模型在这种情况下效果并不明显;而在开放区域的停车位数量超过28时,从图6中可以明显看出,路径的干涉概率FAN>AAN>APIA,累计冲突概率下降明显。在停车资源分配方案研究时,若在停车位数量比较少,本文所研究的路径干涉概率并不明显适用,在停车要求少时,如方案1的情况,利用不同方法所求出的累计冲突概率下降率很小,故本文所研究的情况主要适用于大型商圈、民航业停车场在高峰时段以及汽车制造业停车场在生产制造后,要求同时、一次性大量的停车背景。

表3 累计干涉概率计算结果表Table 3 The calculation result of cumulative interference probability

表4 仿真数据表Table 4 Simulation results
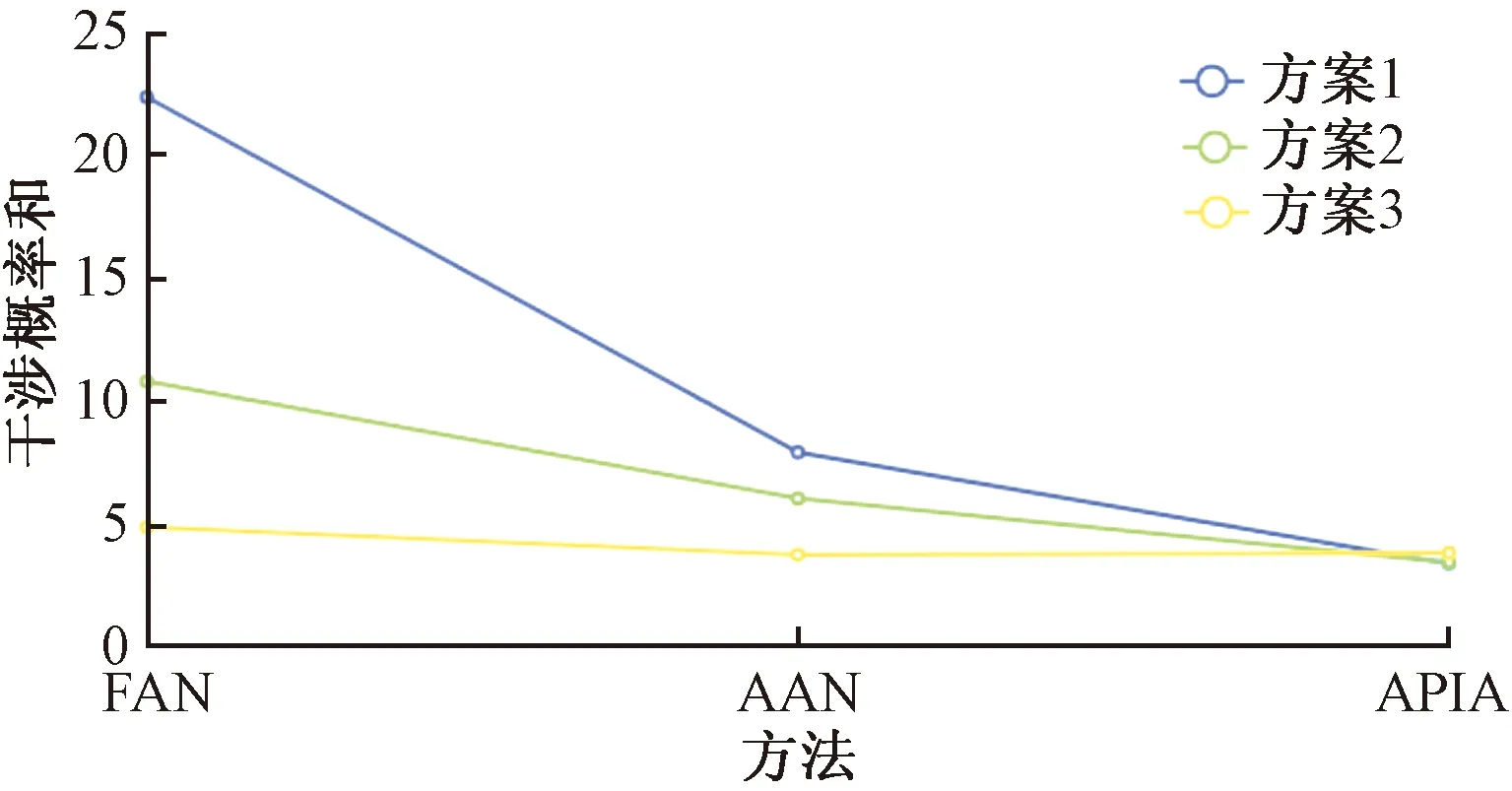
图6 干涉概率计算结果Fig.6 The calculation result of cumulative interference probability
如图7所示,利用Plant Simulation进行投放4辆AGV进行仿真的结果表明,总仿真时长的大小与干涉概率的大小呈正相关关系,图中标识出在方案2运输时,累计干涉概率在减小,随之总仿真时长TPD也随之减小。

图7 4辆AGV仿真结果Fig.7 Simulation results using 4 AGVs for transportation
由图 6可以得出,本文提出的干涉概率模型的效果在停车位数量比较多时比较明显的,故本文着重研究在方案3下的冲突概率与仿真总时间关系。

图8 不同AGV下的仿真时长Fig.8 The Simulation duration under different AGV transportation schemes

图9 等待时间占比图Fig.9 The proportion of waiting time
由图 8可以看出,在方案1下,当只投放2辆AGV时,总仿真时长比较大,且并不随着累计干涉概率的下降呈现TPD:FAN>AAN>APIA,而是FAN>APIA>AAN,这也说明了当只有2辆AGV运行时,AGV之间的冲突比较少,从仿真过程中及图 9可以看出,两辆AGV在大部分时间均处于运行状态,待停车辆在等待的时间占停车总时间的比重很小,停车场的效率较低,故应该继续投入AGV以减少总仿真时长,增加智能停车场的吞吐效率。
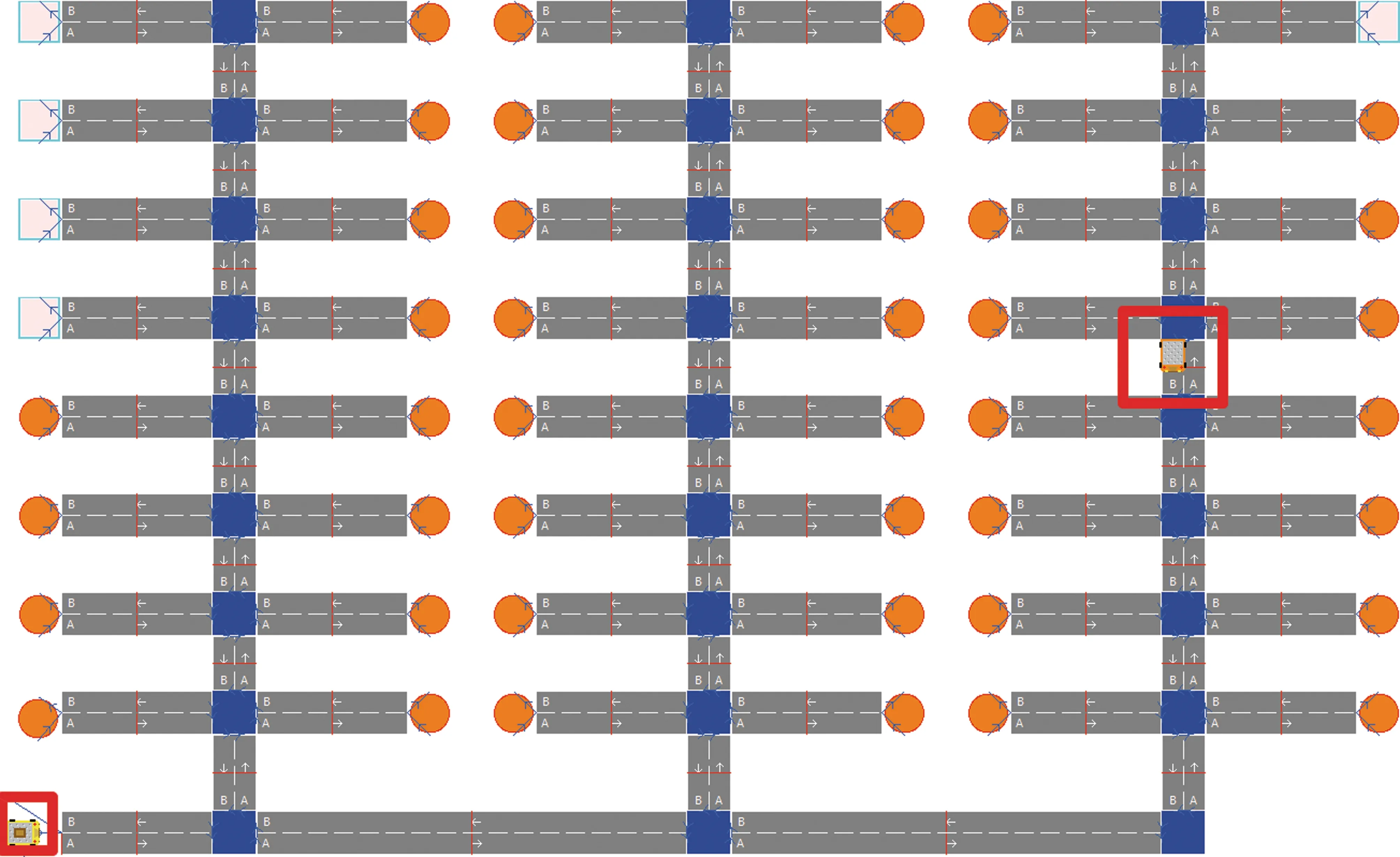
图10 仿真过程图Fig.10 Simulation process
如图 9所示,在投入越多的AGV时,在仿真过程中等待时间的占比是明显增大的,这说明当AGV数量增加时,AGV之间的冲突明显增多,与图 8结合来看,当投入3辆AGV时,等待时间并没有明显增多,而多投入了一台AGV,可以明显增加停车场的运输效率;而当投入4台AGV时,等待时间的占比从25%跃迁至82%,这时投入AGV的效果适得其反,由于AGV之间的冲突明显增多,造成等待时间的增加、停车场的资源浪费,降低了停车场的运输效率。而当使用3辆AGV及以上时,FAN方法的等待时间明显较AAN与APIA方法的等待时间长,而从图 11可以看出,在图 11 (a)中,在3 500 s以后,等待时间出现的频次增多且时间越来越长,而通过AAN和APIA方法对停车资源进行规划后,冲突概率的减小使得AGV的等待时间平均且分散,这是由于FAN方法在分配停车资源时,任务之间的车位非常近,尤其到了后期,任务的停车资源集中在C区,C区的停车位相较于A、B区距离更远,AGV在回到出入口装车后,需等待C区的AGV在停车后经过漫长的路径返回出入口,且随着完成任务越来越多,等待时间就越来越长,如图10所示,在后期停车时,必须等待右上方的车辆经过漫长的主干道,左下方的AGV才能开始任务,而AAN与APIA将相邻任务的停车位比较分散,如图11(b)和图11(c)所示,AGV的等待时间比较分散,并不会出现图 10所示的情况。
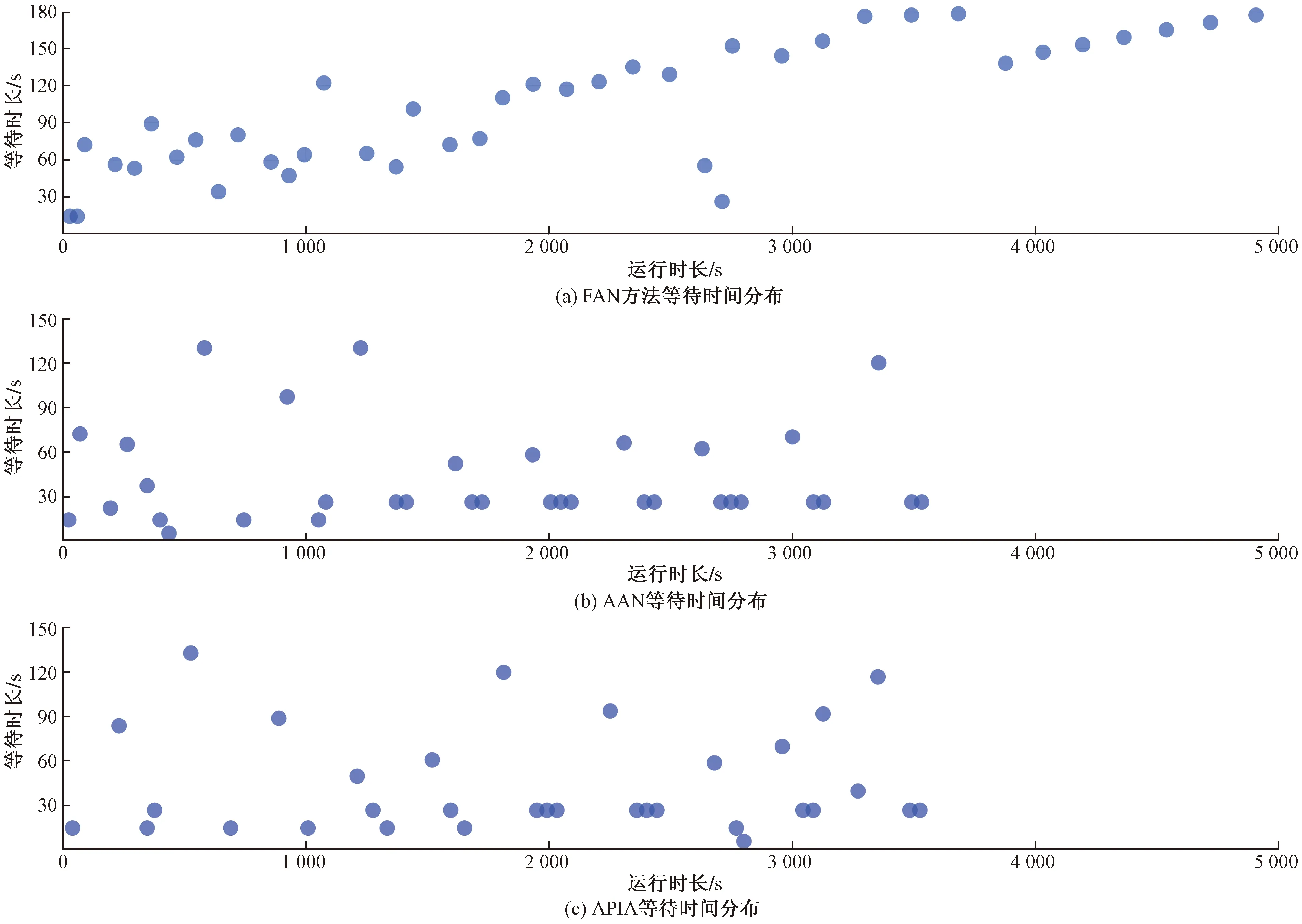
图11 方案3等待时间分布图Fig.11 The distribution of waiting time under different methods
4 结论
停车领域的AGV可以自由地选择终点,而通过对停车资源进行合理分配,通过对AGV之间可能出现的冲突进行预测并减少冲突,可以有效降低AGV的等待时间,提高智能停车场的运输效率。在停车场对停车任务有大量需求时,路径之间的干涉比较多,若不对冲突进行预测,就会造成大量等待时间的浪费。本文做出了以下创新工作。
(1)针对智能停车场可以自由选择终点这一特点,提出了一种全新的停车分配方案代价评价模型,将路径干涉概率模型引入代价评价模型,通过路径干涉概率模型对停车位分配方案进行评价。
(2)针对现有的停车资源分配方法在停车高峰需求的情况下鲁棒性不强的情况,本文提出了基于距离交替分配以及基于遗传算法整体分配两种算法,对停车位进行分配。
经过仿真验证,在44个停车位,投入运输4辆AGV的情况下,通过基于遗传算法的整体分配方法可以将总停车时长降低30.4%。
