基于周期调整负荷成分指数的行业用电大数据价值挖掘

严玉婷，薛 冰，方力谦，黄国权，张勇军

(1.深圳供电局有限公司, 广东 深圳 518001；2.华南理工大学电力学院，广东 广州 510641)

中国能源革命不断向纵深推进，期间数字经济加入并助推能源高效转型，两者的深度融合催生了一种新型经济发展形态——能源数字经济[1-3]。发展能源数字经济，数字化是战略性抓手，数据挖掘是关键出路。而作为社会能源供应的枢纽，电网企业应当充分发挥电力大数据实时监控、直观反馈的特点，分析负荷特性变化进而挖掘其深层价值。

近年来，基于电力大数据的用电分析研究逐渐深入，主要思路为①对负荷曲线聚类以提取典型负荷模式；②提出多个指标捕捉负荷的特定变化；③基于数据驱动方式分析用电行为。文献[4]总结了负荷模式提取常用的对负荷曲线进行聚类的方法特点；文献[5]提出了一种基于深度学习的YLP特征提取，捕获负荷每日和季节性变化，并通过负荷聚类图像观察其全年特征；文献[6-7]计算不同时间尺度下(年/月/日)的负荷率、最小负荷率和峰谷差率等时序特征指标，用以对比描述负荷的特性变化；文献[8]采用三相电压、电流、功率因数等建立多维数据特征，基于Graph模型聚类分析用电用户行为并对用户分类；文献[9]借鉴股市指数计算京电指数，从电力交易角度分析用电特点。

但是，上述研究与用户实际生产行为变化的联系并不紧密，具体表现：一方面上述所提指标均为负荷特性指标，与用户调休、增产等实际生产活动无关；另一方面，仅对精细时间尺度下的日负荷曲线进行聚类，并未对受工作日效应影响的周期波动和受气温影响的随机波动进行分离研究。因此，对于行业大用户用电大数据的挖掘分析，关注其实际生产行为变动能更好挖掘该类用户用电数据的潜在价值。

在证券交易中，股市指数被用于反映股市行情变动，按所包含股票样本数可分为2类[10]：按一定标准选取部分上市股票作为样本的成分指数(如沪深300等)和以全部上市股票作为样本的综合指数(如上证综指等)。在电力大数据环境下，借鉴成分指数，通过科学客观的方法挑选出少量最具代表性的样本用户来降低数据广度，并分析行业大用户群体的用电行为变化是值得探索的方向。

鉴于此，本文旨在构造一种负荷指数，展示行业大用户群体的负荷波动情况，为分析行业用户生产经营状态以及未来经济走势提供数据基础。首先，根据地区实际情况筛选出若干位具有代表性的行业大用户作为样本对象；然后，利用STL算法(seasonal-trend decomposition procedure based on loess)获取样本历史日电量的周期分量，用以计算调整日电量，并提出工作强度系数指标，联系用户生产实际，再按样本所属行业及其个体地位，基于模糊专家评价法等方式赋予多项权重值，综合上述构造企业用户调整负荷成分指数；最后，以深圳市为案例分析负荷指数应用效果。

1 负荷指数样本基础

电力用户成千上万，每日产生大量数据，然而价值密度较低[11-12]，通过筛选其中部分用户的数据来降低数据广度可以提高价值密度。

自改革开放以来，中国经济总量快速攀升的同时发展不平衡问题也越发突出，利润分配在不同行业、不同规模企业上严重失衡，此现象在经济发达地区更为严重。以深圳市为例，2019年地区生产总值(gross regional product，GDP)约为2.7万亿元，而仅中国平安保险集团的净利润已将近0.15万亿元，占地区GDP超5%，营收总额排名前10位企业的净利润总和更是超过地区GDP的20%。在此意义上，少量的大型企业的经营状态即可一定程度上代表地区经济发展的景气程度。因此，分析少量行业大用户群体的负荷特性变化在宏观上具备地区经济表征性。

借鉴股市成分指数，考虑筛选地区若干位具有代表性的企业用户作为样本对象来计算负荷指数。

2 周期调整负荷成分指数构造方法

前述提及，用户实际生产行为变动少有关注，而利润分配严重失衡，这使得简单加和样本用户用电量并不足以支撑深入分析。因此，需要针对上述情况相应处理样本用户日电量。

2.1 负荷指数基础指标

不同于小企业或个体户等，多数大企业尤其是工业大企业一般会实行单休或双休制度，且对于一些大规模的工业企业，其工作计划性强，在季度或月度等中短时间段内每日的工作量基本稳定。因此，部分大企业用户用电量存在着工作日效应，即一周内工作日负荷率明显高于周末日负荷率[13]。这一工作日效应带来的固有周期变化使得用户负荷存在显著的“正常”波动，而这种波动会影响对负荷受扰波动的辨别以及对异常波动严重程度的判断。因此,需要区分开工作日效应这种固有波动的影响，但也不能忽略这部分电量的实际效益。

本文将用户实际日用电量表示成N×7维矩阵D，拆解为

D=F+I·T

(1)

式中F为N×7维的非周期分量矩阵；I为N×1维的全1矩阵；T为1×7维的周期分量矩阵。

T通过STL算法[14]对历史数据进行周期分解得到。STL是一个迭代的非参数回归过程，是将鲁棒局部加权回归作为平滑方法的时间序列分解方法，能够得到稳健的周期项，而不会被数据中的异常行为扭曲，并且适用于有缺失值的时间序列。

STL利用局部加权散点平滑(locally weighted scatterplot smoothing，LOESS)对离散序列点进行平滑处理。对于一个时间序列yi(i=1, 2,…,n)，选取平滑参数q≤n，由与时间点x最近的q个序列时间点xj构造时间点x上的邻近权重：

(2)

式中λq为x与距其第q个远的序列值xλ的距离。

以此对yi局部加权线性回归的优化目标为

(3)

基于LOESS，STL包含内、外2个循环，其中内循环过程如下：

1)去趋势，即减去上一轮结果的趋势分量，D-T(k)；2)周期子序列平滑，对每个子序列做LOESS回归，并向前、后各延展一个周期，得到C(k+1)；3)周期子序列低通滤波，对C(k+1)依次进行窗口长度为7(周期长度)、7、3的滑动平均，再LOESS回归，得到H(k+1)；4)周期子序列去趋势，即S(k+1)=C(k+1)-H(k+1)；5)去周期，即减去周期分量，D-S(k+1)；6)趋势平滑，对Y-S(k+1)进行LOESS平滑，得到趋势分量T(k+1)。

外循环根据上述所得周期项S和趋势项T计算余项R=D-S-T，并由此对时间点x赋予稳健权重：

(4)

(5)

式中 median(·)表示取给定数值集合的中值。

进一步地，为保留周期分量电量带来的实际效益，将T均摊到周一至周日，以日用电量调整值D′代替实际值D作为负荷指数基础指标：

(6)

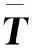
企业用户虽有固定工作日效应，但由于每周任务量的差异会存在工作强弱区别，以ξ描述此种工作强度，其元素ξi的目标确定如下：

mingm=σ(Dm-ξm·T)

(7)

式中Dm为由D中第m行元素组成的行矩阵；σ(·)来计算给定数值集合的标准差。

2.2 样本用户权重确定

利润分配失衡问题使得各行业各企业对主体经济的推动力不一。因此，考量企业用户所属行业及其个体的差异，为样本用户分配多项权重，并据此对其调整日电量进行加权整合。

2.2.1 行业层面

1)地位重要度权重。

相较于一些传统行业的企业用户，社会或是政府更关心一些高新技术行业的发展，同时这些高新技术和行业也汇聚了更多的社会资源投入，具有更高的经济产值。因此，对于这部分用户用电量波动应给予更多的重视。在指数中，结合一种经典的主观赋权法——模糊专家评价法[15]对样本涉及行业的相对重要性划分5个等级，并以梯形模糊数M=(l,m,n,r)量化专家评判意见，其中，l、m、n、r分别为模糊数的下界值、上临值、下临值和上界值，取值如表1所示。

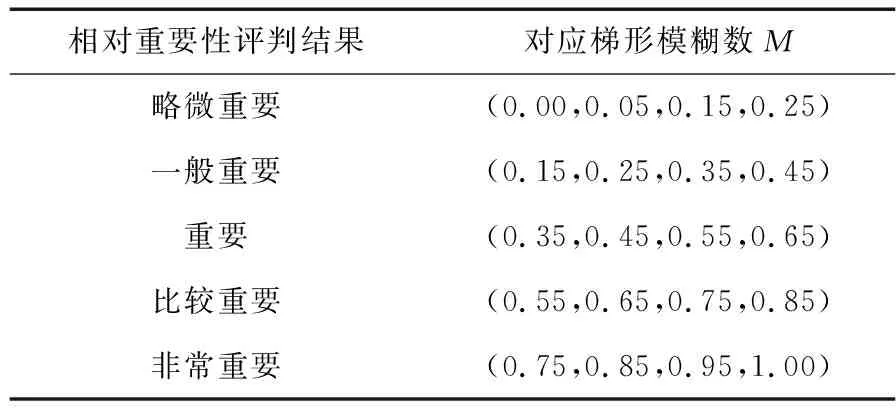
表1 梯形模糊数取值Table 1 Trapezoidal fuzzy value

首先，邀请k位专家评判样本涉及行业的地位相对重要性，将所有专家评判结果对应的模糊数以等权重线性加权方式进行整合，得到第i个行业的重要程度判别模糊数：

(8)

式中Miq为第q位专家对第i个行业的评判结果对应的模糊数。

然后，计算梯形模糊数的重心：

(9)

式中μM(x)为梯形模糊数M对应的隶属度函数，取值如下：

(10)

最后，对c(Mi)归一化即可得到样本涉及行业的地位重要性权重si。

2)行业贡献率权重。

由于地区的发展规划因地制宜，各有行业侧重，使得不同行业对地区经济发展的贡献度不一，因此，对高贡献行业应给予更多关注。定义行业贡献率rC为各行业增加值增量与地区生产总值增量之比，即

(11)

式中 ΔEi为第i个行业的地区行业增加值增量；ΔZGDP为地区生产总值增量。

3)能耗产出关系权重。

高能耗并不与高经济收益完全对等，相比于传统的高能耗产业，高产出的技术型行业更为重要。对此，行业能耗产出关系反映了其对主体经济的贡献度，根据用户所属行业对其赋予经济贡献度权重，该权重计算方式如下：

(12)

式中Ei为第i个行业的地区行业增加值；Pi为第i个行业的样本电量总和；n为样本涉及行业总数。

2.2.2 个体层面

同行业内企业用户间的规模对比很大程度上在其用电量水平上有所体现，因此无需额外考量该因素并赋权。而值得关注的是，企业用户业扩潜力与该用户的发展过程有直接的关系，相比于发展到达稳定期用户，日渐蓬勃的企业更是经济走势的潜力股，应当着重分析。对此提出年化业扩比例kp和容量饱和度SS,p指标，判断第p个用户的业扩潜力：

(13)

(14)

表2 容量使用比例分级靠档Table 2 Category-weighted chart of the capacity usage ratio %

组合kp、SS,p这2项指标，计算第p个用户的业扩潜力权重：

(15)

式中Ωi为第i个行业的用户集合。

2.2.3 权重组合

组合上述业扩潜力权重，得到第i个行业内第p个用户的综合权重，即

ωp=(αsi+βrCi+θρi)·ep,p∈Ωi

(16)

式中 ɑ、β、θ为组合系数，此处取ɑ=β=θ=1/3。

2.3 构造调整负荷成分指数

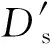
(17)

式中D′sp为第p个用户的调整日电量矩阵总和值；D′sp0为第p个用户于t0日的调整日电量矩阵总和值。

2.4 剔除环境因素影响

环境因素是影响负荷变化的另一主要因素，尤其是气温因素。通过分析负荷与气温的相关性，剔除指数受气温因素的影响。

协变量可以用来解释时间序列中的一些变化，考虑气温因素作为具有时变系数的协变量，其时变系数随时间平稳变化，但不呈现任何周期性。将指数拆解为

It=Lt+τtAt+ζt+ε

(18)

式中Lt为平滑的趋势项；At为协变量，即气温值；τt为协变量的系数；ζt为随机项；ε为拟合误差。

剔除气温因素协变量的影响，即可得到负荷指数的趋势曲线。

3 调整负荷成分指数应用示例

以深圳地区为例，所有用户按2019年总用电量排序，以最大用电量作为基准值的对比结果如图1所示，其中第1位用户与第173位用户的差异已超百倍，与第201位用户差异更是将近千倍。因此，剔除用电量排序200名外的用户，再参考行业挑选出深圳市100位企业用户作为样本构造2020年指数，电量数据规模大小由全量用户的365×106维矩阵缩减至100位用户的365×100维矩阵，样本涉及行业及其代号对照如表3所示。

图1 用电量排序结果Figure 1 Power consumption sorting result

表3 样本涉及行业及其代号对照Table 3 Industries of samples and its code

首先，对样本用户前一自然年(2019年)的历史日电量进行STL分解，获取样本用户历史日电量的周期分量，并据此对用户2020年实际日电量进行调整，得到调整日电量D′。某用户调整前、后的电量曲线如图2所示，可见该用户调整负荷值虽仍有细微波动，但与调整前负荷的波动性质已截然不同，不再表现出工作日效应，即不再固定于休息日大幅跌落至极小值。同时，由此得到的100位用户的工作强度系数矩阵如表4所示。

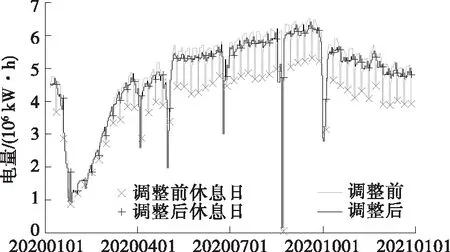
图2 某用户调整前、后用电量对比Figure 2 Power consumption before and after adjustment

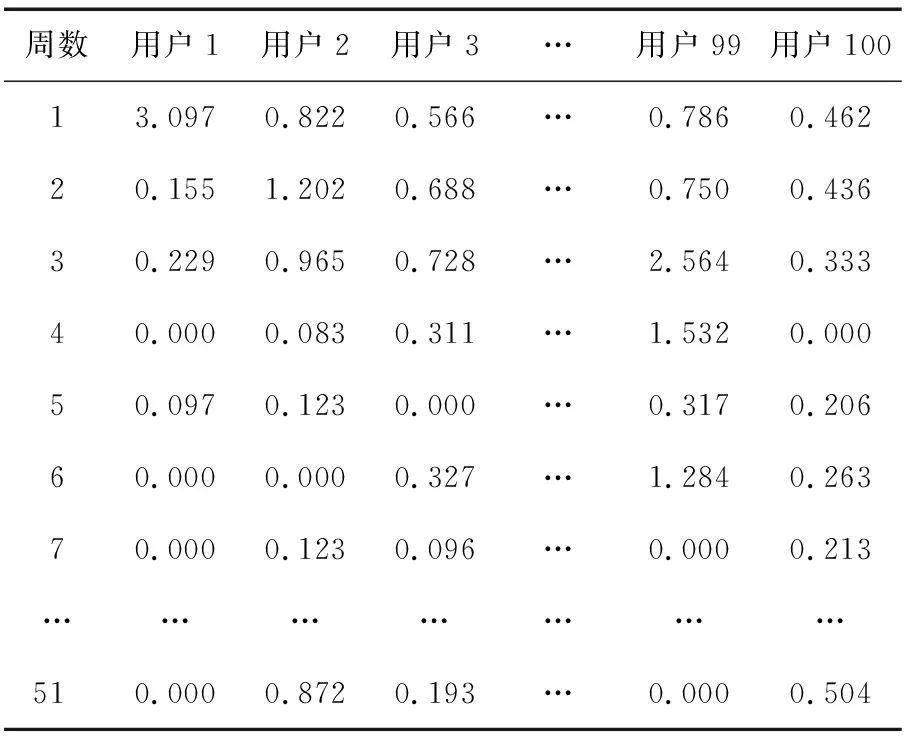
表4 工作强度系数矩阵Table 4 Matrix of working strength coefficient

然后，确定各样本用户涉及行业的权重。在深圳市统计局网站上查询行业增加值增量及样本电量总和等数据，如表5、6所示(由于2019年统计数据不全，就近取2018年数据作为代替计算)。

表5 2018年样本涉及行业增加值增量及电量总和Table 5 Increment of value added by the industries of samples and total power consumption in 2018

表6 2018年地区生产总值增量Table 6 Increment of the regional GDP in 2018

采用问卷调查的方式咨询专家意见，根据供电局客服经验丰富的5位专家意见结果，按式(8)～(10)计算模糊数重心大小，得出行业重要度权重，如表7所示。结合表5、6，按式(11)、(12)可计算行业贡献率、能耗产出关系权重；根据100位企业用户近3年的容量扩装情况计算其业扩潜力权重。

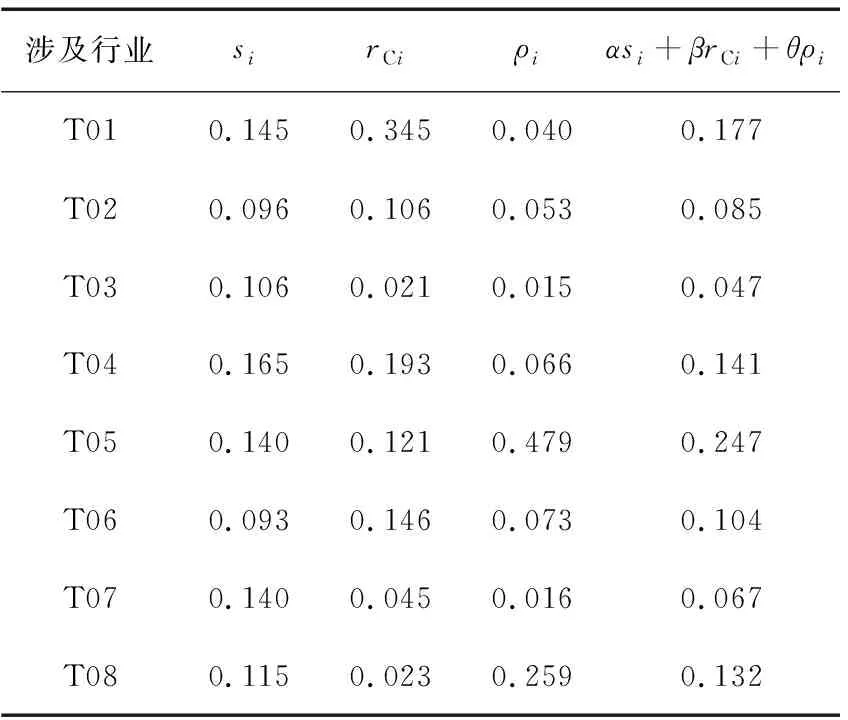
表7 行业权重值Table 7 The weights of industries of the samples

最后，整合上述权重并结合式(16)对企业2020年调整负荷进行计算，以2020年1月6日作为基期绘制指数，如图3所示，进一步地，可去除气温因素影响的指数。

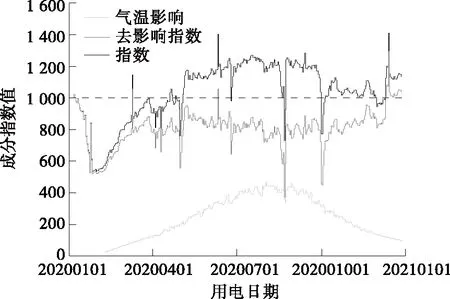
图3 2020年指数及气温影响情况Figure 3 Index and its temperature impact in 2020

4 调整负荷成分指数示例分析

4.1 用户工作强度分析

基于上述所得100位用户的工作强度系数矩阵(表4)绘制热力图，如图4所示(图中色度于0～1为均匀分布，于1～10为对数分布)，其中，每行代表一周，每列代表一位用户，每个色块的颜色表示用户某一周的工作强度系数，系数值越大，说明用户当周工作量越大。

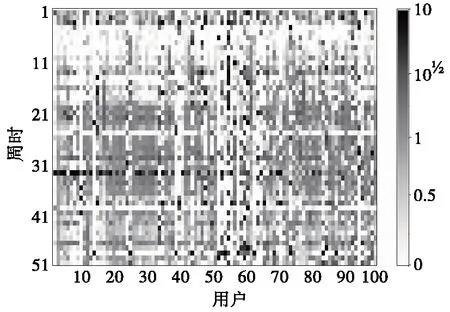
图4 2020年各周用户工作强度情况Figure 4 Weekly working strength in 2020

由图4中可见，第4至第8周(2月份)基本所有用户工作强度系数接近0，当时处于春节期间，且受疫情影响直到3月才陆续复工复产，能看出部分企业疫情调休，复工复产后仍有几周无工作日效应；第14、16、24、39周同样出现了大部分用户工作强度系数降至0的情况，其中，第14、16、24周分别为劳动节/端午节前后周，均于周末调休补班，而第39周为国庆节当周，假期工作暂停。

综上，所提工作强度系数在分析用户复工复产、工作安排、调休补班等生产经营行为上具有重要作用。具体地，当工作强度系数接近1时，该用户当周处于正常生产经营状态；当接近0时，该用户当周处于调休补办或假期状态；当远大于1时，该用户当周生产经营活动较平常更为活跃。

4.2 地区日用电行为模式分析

当去除工作日特性的短期规律波动后，指数的趋势更为明显，可以清晰辨别用户电量的整体水平和异常波动。如：2020年大部分时间下去气温影响指数值低于1 000，以电量角度来看，地区发展整体处于低迷状态，直至年底有所恢复；再如：1月底春节期间指数跌至550左右，之后受疫情影响直至3月中旬指数恢复至1月水平，说明大企业才基本实现复工复产；又如：指数在春节、劳动节、端午节、国庆节4个法定节假日前后明显下跌，其中下降幅度为春节>国庆>劳动节>端午节，这方面指数也侧面反映了对节假日的重视程度。

此外，将2020年指数值与该年全社会总电量(以1月1日值标准化)对比，如图5所示，可见原始指数与全社会总电量具有相似的变化趋势，具有表征整体用户用电行为的作用。

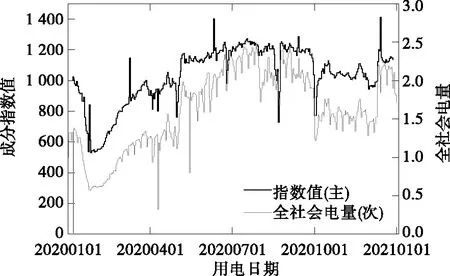
图5 2020年指数值与全社会总电量对比Figure 5 Index and total electricity consumption in 2020

综上，通过对比指数值可比较地区电量变动情况，一定程度上能反映地区发展态势，当指数长期处于增长状态则说明地区生产经营行为趋于活跃，发展向好，相反则说明地区发展较为低迷。

4.3 指数与经济关系格兰杰检验

为进一步验证指数对地区经济的表征性，本文探讨指数与地区GDP、固定资产投资(investment in fixed assets，FAI)、规模以上工业总产值(gross output value of industry above designated size，IDGO)以及居民消费价格指数(consumer price index，CPI)等指标间的关系。

计量经济学中的格兰杰因果检验[16]可用于判断2个时间序列变量在统计学上的因果关系。利用格兰杰因果检验可分析去除气温影响后的指数与多个经济指标间的关系。基于卡方分布对指标与指数间关系假设进行检验，在1%的显著性水平下作三阶最大滞后数检验，并与未经加权处理的指数检验作对比，取显著性水平最小的滞后阶数结果，如表8所示；GDP与指数的相关性如表9所示。

表8 Granger因果检验结果Table 8 Granger causality test results

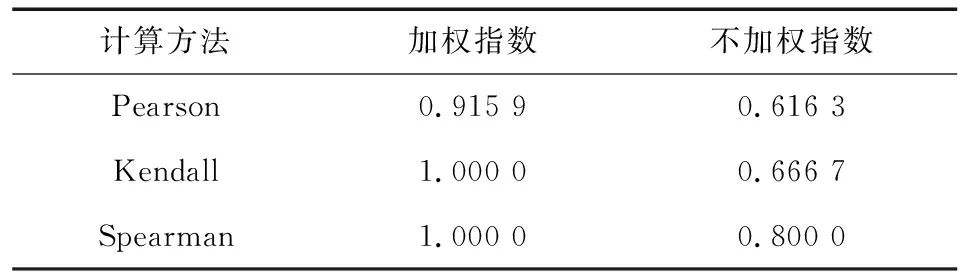
表9 GDP与指数的相关系数Table 9 Correlation coefficient between GDP and index

格兰杰检验结果显示，指数是引起IDGO、CPI等变化的Granger原因，并且均具有三阶的滞后，故负荷指数所表征的用电行为变动可在一定程度上反映生产总值以及消费水平的变化；FAI是引起指数三阶滞后变化的Granger原因，说明了固定生产投资对生产经营行为起到规划作用。在GDP与指数的相关性分析中，多种方法均说明指数与GDP高度相关。同时，在指数加权与否的对比中发现，加权指数与经济指标关系检验结果的显著性水平更低，即结果更为可信，且加权指数与GDP的相关性也优于不加权指数的相关性，由此证明了加权方法的有效性。此外，指数与经济值的关系也印证了样本选取具备良好的表征性。

5 结语

本文借鉴股价指数，构造了调整负荷成分指数，旨在展示行业大用户的电力负荷发展情况，指数大于1 000时说明用电量比基期有所上涨，对比两日指数值可比较用户日电量变化情况。

1)指数构造过程所得到的工作强度系数在分析用户复工复产、工作安排、调休补班等生产经营行为上具有重要作用；2)指数反映地区日用电行为模式时具有更加准确直观的可视性，具有表征整体用户用电行为的作用，且一定程度上能反映地区发展态势；3)去除气温影响后的指数与经济等指标具有明显的统计因果关系，能够为投入产出关系分析以及经济走势预测提供参考价值。

未来可在调整负荷成分指数的基础上研究更细化、分类别的电力负荷指数，专门针对不同行业、不同体量、不同类型的用户制定指数曲线，通过提炼指数背后的经济价值为各方决策提供有效支持。