基于KLDA-INFLO的继电保护整定数据异常识别方法

董小瑞，孙 伟，樊群才，李 鑫

(国网山西省电力公司运城供电公司，山西 运城 044000)

近年来，由于电网互联、大规模间歇式能源的并网运行、柔性交流输电系统的投运，使得电力系统的结构、协调控制日趋复杂，导致电力系统的安全稳定运行问题愈加突出[1-2]。而作为电网安全稳定运行必不可少的二次设备之一，确保继电保护系统正常运行状态的重要性日趋上升。

为此，研究者们针对系统运行状态的检测评估提出了多种途径。文献[3]利用局部放电信号实施继电保护设备异常工作状态的检测；文献[4-5]采用继电保护设备的红外图像进行缺陷探测分析；文献[6-7]通过巡查机器人进行继保设备的异常状况挖掘。此类方法具有检测准确、能够及时处理等优势，但也存在成本预算高、落地难度大等限制。

通常，继电保护系统运行过程中潜在的突然改变常常会引起运行参量的波动，例如电流、功角、频率、功率等。这类数据的波动往往预示着系统运行状态的扰动，是故障发生的先兆，严重威胁着继电保护系统的正常动作。随着基于相量测量装置(phasor measurement unit, PMU)以及测量系统(wide area measurement system, WAMS)技术的日趋成熟，已能够实现全网同步采集机组和线路信息，记录系统的动态过程并提供扰动触发的暂态运行状态数据，为系统安全稳定评估与监控提供了强有力的信息支撑[8]。因此，利用动态监测数据对继电保护系统扰动进行分析是可行解决途径之一[9]。

近年来，基于运行数据进行系统异常状态检测成为学者研究的重点方向之一[10]。文献[11]利用高斯混合聚类针对电力工控系统进行异常检测；文献[12]设计了云计算电力异常大数据检测系统；文献[13]结合粒子群优化BP神经网络和改进谱聚类进行异常数据检测；文献[14]建立了层次光伏异常运行扰动检测模型；文献[15]通过云理论分析智能电表故障。上述方法能够较好地实现系统异常运行状态检测，有效改善成本及可行性，但在高维度、多设备的场景中，方法的全面性还可进一步地提升。

为此，本文结合基于核函数的线性判别分析(kernel linear discriminant analysis，KLDA)模型和被动式异常因子检测(influenced outlierness，INFLO)异常检测模型，针对继电保护系统提出运行状态数据异常检测方法，其中，实施高维度输入数据的降维，并以运行参数正常数值范围作为稳定区域，发掘偏离该区域的异常节点，从而对异常运行状况做出快速反应。基于某区域配电网中的继保设施监测数据进行实例仿真分析，论证该方法具有较好的异常检测性能，能够有效识别潜在运行扰动信息。相较其他模型，该方法的优势在于能够基于相同流程应对处理继保系统中不同设备、参数的异常排查，有效提升全面性和可行性。

1 基于KLDA的数据降维模型

为进一步地加以分析与应用，输入数据必须经过相应预处理环节，从而能够提供内容有效、规模较小、较为纯净的训练与测试数据，其中，对于输入数据的降维是数据预处理的关键步骤。考虑到数据的非线性特性，采用基于KLDA的方法寻求最佳投射方式，求解出相对重要的输入特征，以实现降低运算负担、加快反应时间、易于将结果视觉化的目的。

1.1 线性判别分析模型的构建

线性判别分析(linear discriminant analysis，LDA)模型是一种有效的模式识别算法[16]，其本质思路是以最大、最小化样本类内间距为原则，将高维特征样本投影到可分离性最佳的鉴别矢量子空间，达到特征抽取与特征空间维数缩减的目的。LDA通常基于 Fisher 准则函数实现数据点的投射，继而实现降维的目的。

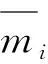
(1)

(2)

可以看出，投影后的中心点就是样本中心点的投影。理论上来讲，使得投影后的数据中心点距离最远的时候即为最佳投影，此时得出优化函数：

J′(w)=|WT(m1-m2)|

(3)

以二维数据为例，数据点投影方式分为2种，如图1所示，若数据点采用图1(a)投影方式，则投影到接近X1轴的直线上时，能够确保投影后类别间距较大，但会导致类别间有重叠，故不同类别可分离性较差；相反，若采用图1(b)投影方式，则投影到接近X2轴的直线上时，尽管类别间距较小，但不同类别间可分离。因此，优化目标的过程中还要考虑方差，方差越大越难分离；方差越小越能达到预期目标。

图1 数据点投影Figure 1 Possible projections of data points

定义投影后的方差为

(4)

因此，目标优化函数可写为

(5)

进一步化简为

(6)

求解特征解可得：

(7)

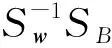
1.2 核函数的设计

核函数Kernel是对映射空间相似性的度量，其数学表达为

k(x,x′)=〈φ(x),φ(x′)〉

(8)

Kernel可用作任何在点积或相关范数过程中定义的泛化[17]。较为常见的是使用Kernel 作为基础的支持向量机(support vector machines，SVM)、高斯过程(gaussian processes，GP)、神经网络(neural network，NN)等。

Kernel主要通过一个映射函数φ将数据从输入空间映射到一个特征空间，这种映射能够确保数据变得更加容易分离，继而促进LDA的运行效果，如图2所示。

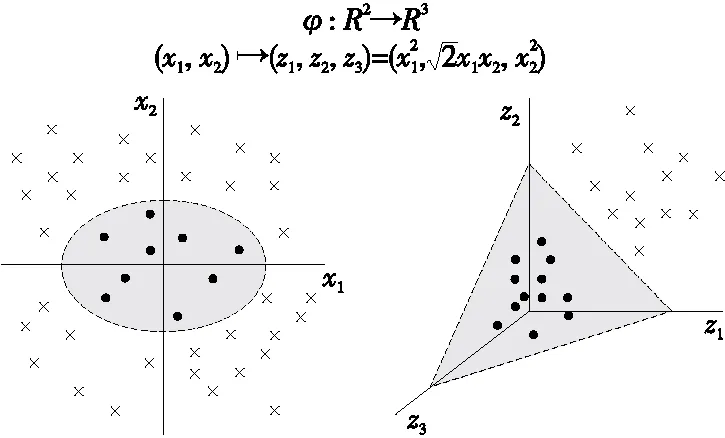
图2 核函数Figure 2 An example of Kernel function

常用Kernel函数包括Linear、Radial basis以及Sigmoid等。依据应用场景中潜在数据呈非线性分布的特点，本文选择Sigmoid，其数学表达为

(9)

其中，c为常数，可控制低阶项的长度，本文取1。

2 基于INFLO的数据异常检测模型

2.1 基于数据密度异常检测设定

基于密度的异常数据检测方法通常将数据点分为3类：核心点、边界点、噪声点，如图3所示。基于此，异常检测算法将相互间距离小于Eps的数据点置于一个簇内，与核心点距离小于Eps的边界点被置于该核心点的簇中，而大于或等于Eps的则为异常或噪声点。

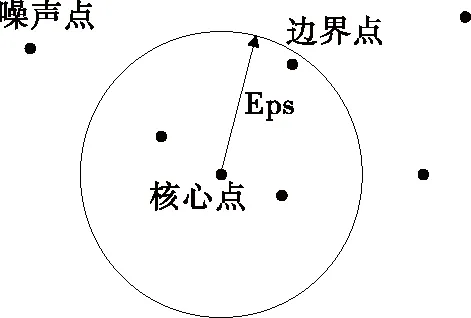
图3 密度异常检测原理Figure 3 Illustration of outlier detection by data density

2.2 基于局部异常因子的异常检测

局部异常因子(local outlier factor，LOF)算法主要依照局部密度来划分[18]。通过比较单个数据点和其周边点的局部密度值，相近点被组合在聚集区域而处于明显较低密度区域的点则被剥离出来，并被划分为异常点。其中，用于衡量局部密度的距离一般被称为可触及距离。假设dk(A)为数据点A和第k个最近周边节点之间的距离，则可触及距离(reachable distance, RD)可表示为

Rk(A,B)=max{dk(o),d(A,B)}

(10)

式中B为核心节点。

由式(10)可知，数据点A的RD为A到B的距离，但不能小于dk(A)。基于此，可推导数据点A的局部可触及密度(local reachable density，LRD)，其数学表达为

(11)

式中k(A)为数据点A的k个近邻点；Card(k(A))为满足数据点A的k近邻域内所有数据点的基数。

由式(11)可得，数据点A的LRD实际是到其全部k个邻近点的平均可触及距离的倒数，即A可以被所有邻近点触及到的距离。将LRD与邻近节点加以比较，可得数据点A的LOF异常判据，其数学表达如下：

(12)

式中Pk(A)为A点是否为LOF异常点的判据分值。若Pk(A)得分值约等于1，则证明该节点所在区域密度和邻近区域相差不大，即为稳定点；若大于1，则代表为异常点。

2.3 INFLO异常检测模型的建立

一方面，对于多数系统而言，数据点的正常与否并不需要一个明确的界限。因此，仅需对产生最大不利影响的异常数据点加以检测，从而可不计一些影响极小的异常点。基于此，实施异常检测运算时无需为针对所有数据点进行甄别，在监测获得足够范围的异常点后即可停止运算，从而大大降低运算成本；另一方面，在某些情况下，不同密度的数据聚集区域间的距离较短，会对LOF的判断产生影响[19]。如图4所示，节点B相较节点A或C拥有更大的Pk值，但实际上A和C才是异常点。

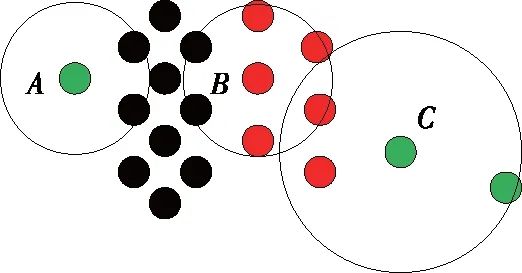
图4 不同簇密度影响示意Figure 4 Illustration of impact of densities in different groups

针对LOF在上述运算成本和误判概率这两方面的限制，本文采用改进后的INFLO算法实施数据异常检测。一方面，与LOF算法不同，INFLO通过设立运算结果上、下界限，并将结果自下限开始增加的形式记录异常检测阈值内的结果，到达阈值后即停止运算；另一方面，在INFLO算法中，邻近区域节点的对称关系被加以考虑。假设节点A的影响范围为ϑ(A)，则ϑ(A)同时包括其knn区域k(A)以及逆knn区域kR(A)，以图5为例，ϑ(A)={B1,B2,B4}。

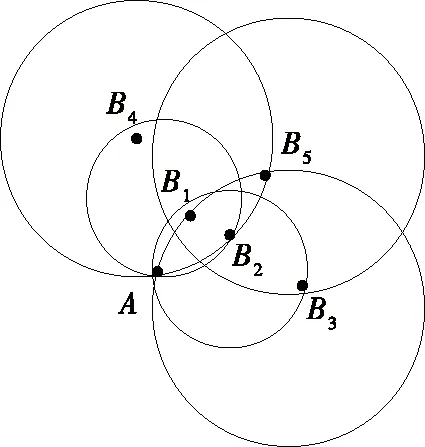
图5 数据点A作用范围图例Figure 5 An example: influence range of a data point A

此外，可定义数据点A的自身密度为

EGCG通过抑制谷氨酰胺代谢通路抑制结直肠癌细胞的生长的实验研究……………………… 李 哲，钱佳乐，向 敏，等（3·166）

(13)

结合上述讨论，INFLO异常判据可由节点在周边区域内的平均密度和自身密度的比值求解，其数学表达为

(14)

式中Ik(A)为A点是否为INFLO异常点的判据分值。若其值约等于1,则证明该节点所在区域密度和邻近区域相差不大，即为稳定点;若大于1,则代表为异常点。

3 算例分析

本文依据位于中部某省某10 kV配电网中的继电保护系统进行示例仿真，分别面向运行扰动以及不合理整定数值的检测。为此，采用两类数据：①该继保所在系统的运行数据，共计6 210组，包括电压幅值、频率、功率因数、峰期和谷期运行电流等，如表1所示；②该系统中不同保护装置过流保护整定值，装置共计101处，包含过流Ⅰ、Ⅱ、Ⅲ段电流整定值,如表2所示。以系统运行状态中的频率、电压2个特征为例，随机采用1 500个数据组，基于KLDA-INFLO方法的检测结果如图6所示。

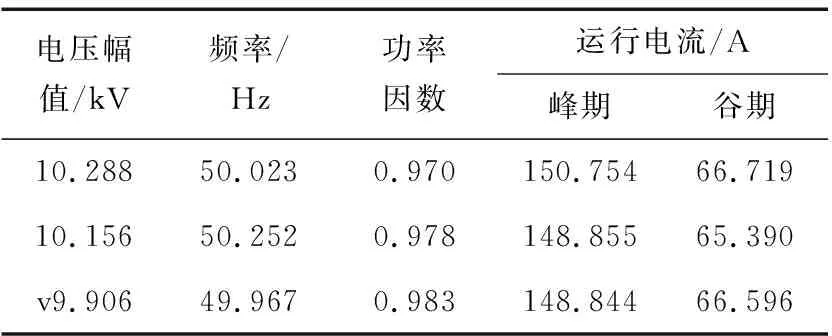
表1 运行数据示例Table 1 Example data of operational conditions

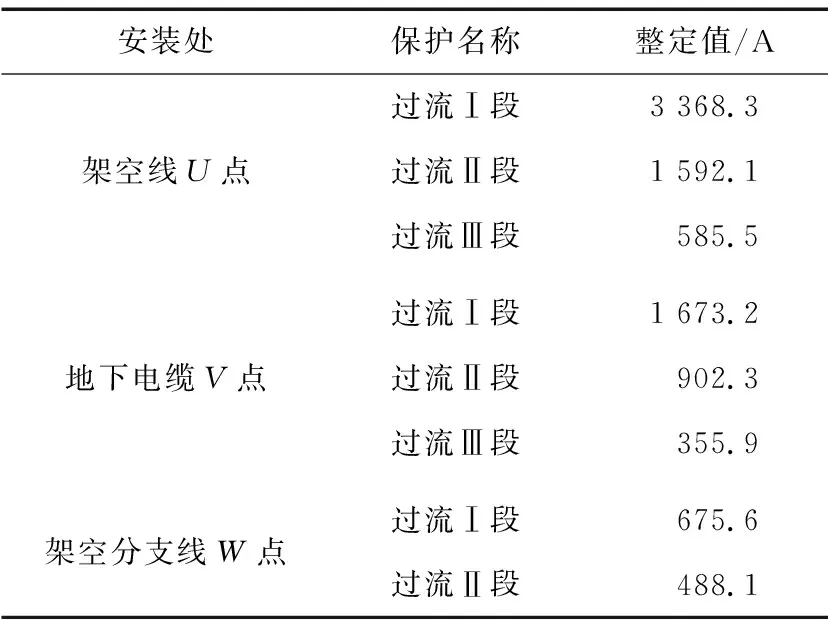
表2 整定数据示例Table 2 Example data of relay setting

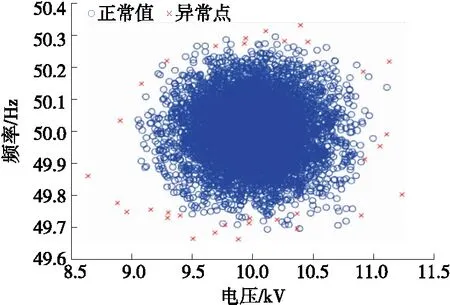
图6 KLDA-INFLO图例Figure 6 An example of KLDA-INFLO output

针对全部两类数据实施仿真验证，将每一组数据所在时刻是否实际出现扰动，以及每一处设施实际存在不正常定值作为验证指标，并分别定义为“1”和“0”。为测试所提出KLDA-INFLO方法的检测性能，将仿真结果分别与未采用降维处理的INFLO方法、LOF模型以及基于密度的DBSCAN算法的仿真结果进行比对，如图7所示。

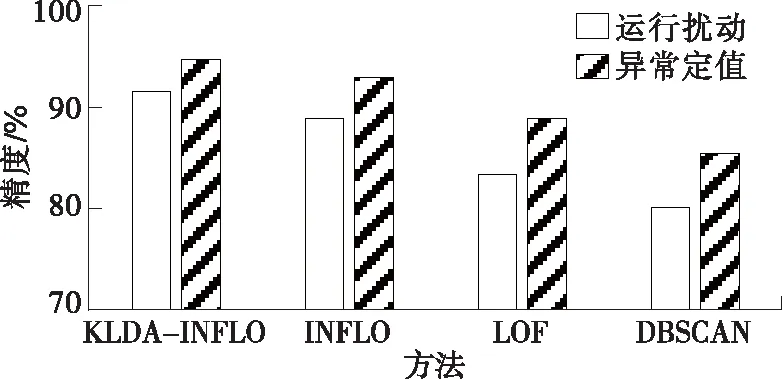
图7 异常检测结果对比Figure 7 Performance comparison of outlier detection

4 结语

本文针对继电保护系统中潜在的运行扰动与整定异常，提出基于数据挖掘的异常检测算法，能够较好地应对多维度数据下的异常情况监测与预警。

1)构建KLDA模型，实现原始数据的降维处理，能够有效应对高维数据环境，并实现降低运算负担、加快响应时间的作用;

2)设计INFLO方法，直接依据运行整定参数正常范围及时检测异常数据，无需具体区分系统中的不同场景、设备，可以全面有效地针对异常状况做出快速反应。