基于格兰杰因果与ARDL模型的高能耗产业用电量预测

沈 豫,黄夏楠，刘 林，胡臻达，顾 玖，蒋传文

(1.国网福建省电力有限公司经济技术研究院，福建 福州 350012；2.上海交通大学电子信息与电气工程学院，上海 200240)

电力行业是国民经济的基础行业，产业经济的发展与电力消费有着密切的联系，挖掘两者之间的关联关系，有利于合理规划产业集群周边的电力发展、提高产业用能经济性，从而助力产业经济健康发展[1-2]。随着“双碳”目标的提出，产业节能减排得到社会的高度关注，高能耗产业作为地区用电量的风向标，更是电力部门关注的重点。对高能耗产业开展用电量预测研究，可以及时发现高能耗产业在生产过程中存在的问题[3-5]。

电力消费与经济发展的关系作为电力经济研究的关键问题，传统的做法是以计量经济学模型作为基础，对电力经济数据进行分析，典型的方法是基于时间序列的计量模型[6-7]。文献[8]以安徽省作为研究对象，采用了多源回归模型对经济增长与用电量偏移的原因进行分析，得到了影响电力消费的多类经济指标以及各指标的影响强度。而文献[9]以北京作为研究对象，以多部门的经济与电力数据建立Granger因果关系分析模型，结果显示：总体上存在经济对能源消费的单向因果关系，不同产业的关系各不相同。文献[10]基于新型分位数方法对1995—2015年的统计数据分析，结果表明工业产值与电力消费存在正相关关系；文献[11-12]采用HP滤波技术对实际GDP的趋势成分、周期成分的处理，研究结果表明能源消费与GDP之间存在协整关系；文献[13]则分析了电力消费与固定资产投资、人均可支配收入等经济指标之间的协整关系。上述分析结果可以看出，对于时间序列数据的研究，不同的时间区间、变量类别、计量分析模型都对分析结果有着极大的影响。另一方面，目前大多数的计量研究主要是分析能源总量与经济总量之间的关系，并没有考虑到具体地区的细分产业经济发展的特点，使得模型的构建不够精细化，误差难以缩小。

负荷预测问题同样是长期以来电力行业的研究热点，大体上可以分为基于数理统计的预测方法和基于人工智能的预测方法。数理统计的方法主要以时间序列分析法[14]、回归分析模型以及灰色模型[15]为主。应用于电力负荷预测的人工智能算法包括长短期记忆网络模型(long short-term memory network, LSTM)[16]、支持向量机(support vector machines, SVM)[17]、神经网络模型[18]等。数理统计的方法对于数据的解释性更强，可以挖掘负荷历史数据与其他外部变量之间的关联性，在处理数据量小的问题时适应性较好；而人工智能方法虽然对预测结果有着更高的精度，但是其对于模型的解释力却略显不足。

基于上述分析，本文以高能耗产业作为研究对象，研究产业用电量与经济发展指标之间的关联与影响。首先根据产业划分原则，建立产业用电量与经济指标的对应关系；基于协整—格兰杰因果关系检验方法，分析高耗能行业电力消费与经济指标数据的之间的相互影响关系，并构建多元经济指标与细分产业用电量的自回归分布滞后(autoregressive distributed lag，ARDL)模型，对地区高能耗产业的用电量进行预测，以实际用电数据对算法精度进行验证，从经济性的角度解释预测误差的来源。

1 产业经济与电力大数据的关联指标选择

1.1 产业电力消费数据细分

在中国《统计年鉴》中，电力平衡表是反映国家或地区的电力供应和消费的重要指标，其中，电力消费量统计量则反映着地区的电力负荷的情况。将地区的用电量比作整体，当对地区电力负荷进行预测时，仅仅考虑对地区总体的电力负荷预测，而不对负荷各分量的变化进行量化分析，则很有可能造成预测的误差较大[19]。而以具体的产业作为研究对象，其用能模型的影响因素较少，自变量与因变量之间的关联性更强。

1.2 产业经济指标细分

采用分行业的方式对某省的经济发展状况进行再划分，可实现更细化的研究。本文列出以行业划分的时序经济指标，如表1所示,可以看出，对于每一个用于刻画某地区经济状况的经济指标都可以按照分行业的方式进一步细分，这与电力消费统计量的划分原则一致，为后续研究提供基础。

表1 产业经济指标分类Table 1 Industrial economic index classification

1.3 基于协整—格兰杰因果关系的指标关系分析

本文运用计量经济学中时间序列分析方法，包括平稳性分析、协整检验以及Granger因果关系检验等，其流程如图1所示。

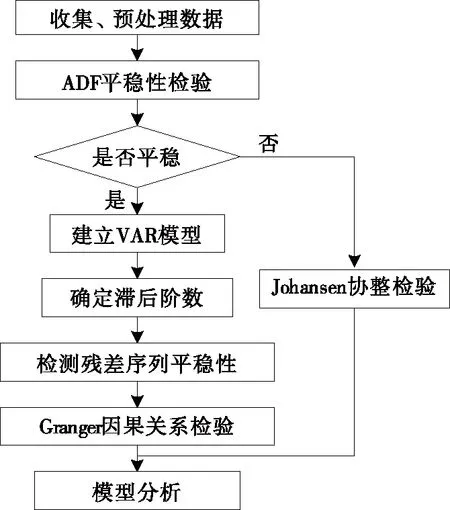
图1 基于协整及Granger因果关系分析Figure 1 Analysis flowchart based on the cointegration and Granger causality analysis

在对时序数据收集后，首先需要对数据进行预处理，去除异常数据。然后采用ADF检验对数据做平稳性分析，若平稳，则可直接建立VAR多元平稳时序模型以及Granger因果关系检验对数据进行回归分析；若数据非平稳，则需要使用协整分析，当数据间存在协整关系时，则可构建Granger因果关系检验，若变量间不存在协整关系，则为“伪回归”，Granger因果检验失去意义。

1.3.1 单位根检验

一阶自回归模型(autoregressive model，AR)为

yt=c+αyt-1+ut

(1)

式中c为截距；ut为期望为0的误差；α为自回归系数；yt-1、yt分别为t-1、t时刻的观测值。

单位根检验：AR(1)模型中yt-1的参数是否为1，目的是对时间序列数据的平稳性检验。若yt为单位根过程，则yt为非平稳序列。DF检验原假设与备择假设为

(2)

ADF检验是DF检验的推广，即考虑AR(p)模型的平稳性，其原理与DF检验类似，不再赘述。

1.3.2 向量自回归(VAR)模型

多变量的因果关系检验可以通过构建VAR模型进行测试，VAR模型是将单变量自回归模型推广到多变量组成的向量自回归模型，典型的p阶滞后的VAR(p)模型为

Yt=C+Φ1Yt-1+Φ2Yt-2+…+ΦpYt-p+Ut

(3)

式中Yt=[y1,t-i,y2,t-i,…,yn,t-i]T(i=1，2，…，p)为滞后第i期的n维变量y1,t-i、y2,t-i，…，yn,t-i组成的向量；C=[c1,c2, …,cn]T为n×1维常数向量；Ut=[u1,u2, …,un]T为n×1维随机误差列向量；Φi(i=1,2,…,p)为n×n维自回归系数矩阵，即

1.3.3 Granger因果关系检验

Granger因果关系检验是一种假设检验的统计方法，检验一组时间序列x是否为另一组时间序列y的原因，利用x的历史数据提高对y变量的预测能力。

令x、y为广义平稳序列，先建立y的p阶自回归模型，再引入x的滞后期建立增广回归模型，即

(4)

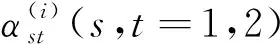
1.3.4 协整关系分析

协整关系是指多个非平稳时间序列变量的线性组合形成的变量是平稳时间序列。协整检验的方法主要有Engle-Granger(E-G两步法)、Johansen协整检验法，其中，前者协整适用单个协整关系的检验，而后者适用于多个协整关系的检验。

2 高能耗产业电量预测模型建模

2.1 预测模型的框架

产业电量预测模型的建模思路如图2所示，分为数据预处理、产业用电分类、细分产业用电量预测3个部分。

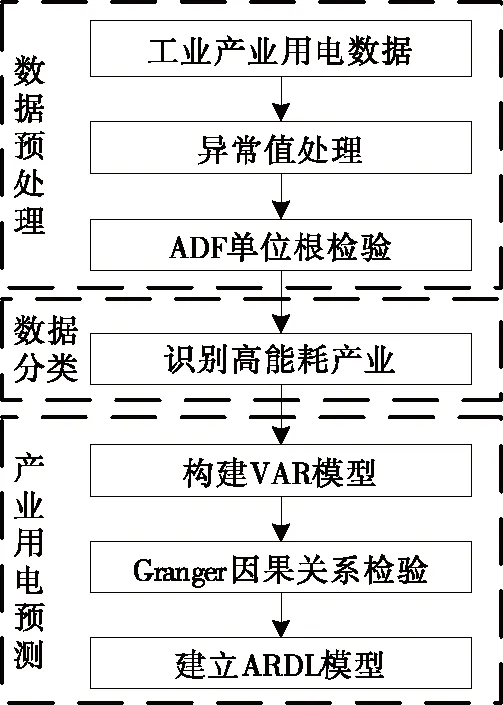
图2 高能耗产业用电量预测流程Figure 2 Flow chart of electricity consumption forecast for high energy consumption industries

1)数据预处理。首先对收集到的地区工业产业用电数据的异常值进行识别和处理，然后通过对比用电数据的同比增长率，确定该月度用电数据是否存在异常。

2)产业用电分类。结合地区电力部门统计的行业用电数据，包括产业月度用电量、用电装接容量、单位GDP电耗等数据，最终确定高能耗行业为非金属矿物制品业、黑色金属冶炼和压延加工业、纺织业、化学原料和化学制品制造业以及有色金属冶炼和压延加工业。

3)产业用电量预测。针对高能耗产业选取经济指标数据，包括主要产品产量、主营业务收入及利润总额。对细分产业构建VAR模型并进行Granger因果关系检验，基于此建立产业用电量预测的ARDL模型。

2.2 高能耗产业ARDL模型

ARDL模型最早由Charemza[20]等提出，在Granger因果关系检验结果的基础上，将高能耗产业中具有较强因果关系经济指标变量作为构建模型的首选变量，建立ARDL模型为

(5)

式中α为常数；φi、βjkljk为系数；vt为白噪声；p、qjk为最大滞后阶数；yesum,t、yesum,t-i分别为t、t-i时期地区高能耗产业的总用电量；xjk,t-ljk为第j个高能耗产业的第k个经济指标变量滞后ljk个时期的值。

3 仿真算例

3.1 数据来源

本文选取2016年1月至2021年6月中国某地区月度用电数据作为产业用电数据集，月度经济数据来源于地区统计局。纺织业是该地区的重点和高能耗产业，其用电量与选取的经济指标如图3所示。

图3 纺织业用电量与典型经济指标Figure 3 Electricity consumption of textile industry and typical economic indicators

由图3可知，纺织业作为高能耗产业，其用电量和经济变量折线图的形状存在一定程度上的相似；同时，用电量和经济数据都存在明显的周期性循环波动，且受春节影响明显，在春节期间，产业用电和经济数据都呈现明显跌落。由于数据可能为非平稳时间序列，因此，在进行用电量合计与高耗能行业主要经济指标关系研究之前，需要对原始时间序列数据进行平稳性检验。

3.2 产业用电数据计量经济分析

3.2.1 单位根检验

根据图1对产业的分类，依次对工业中的高能耗产业的用电数据进行ADF单位根检验。yesum、yeh1、yeh2、yeh3、yeh4、yeh5分别表示高能耗产业、纺织业、化学原料和化学制品制造业、黑色金属冶炼和压延加工业、有色金属冶炼和压延加工业以及非金属矿物制品业的用电数据(采用2016—2020年产业用电量数据)。平稳性检验如表2所示，t统计量即T检验，通过t分布理论来比较2个平均数的差异是否显著；P值(P-value)为伴随概率，用于与原假设设定的显著性水平α进行比较。原假设为变量不平稳，若P≤α，则拒绝原假设；反之，则接受原假设。

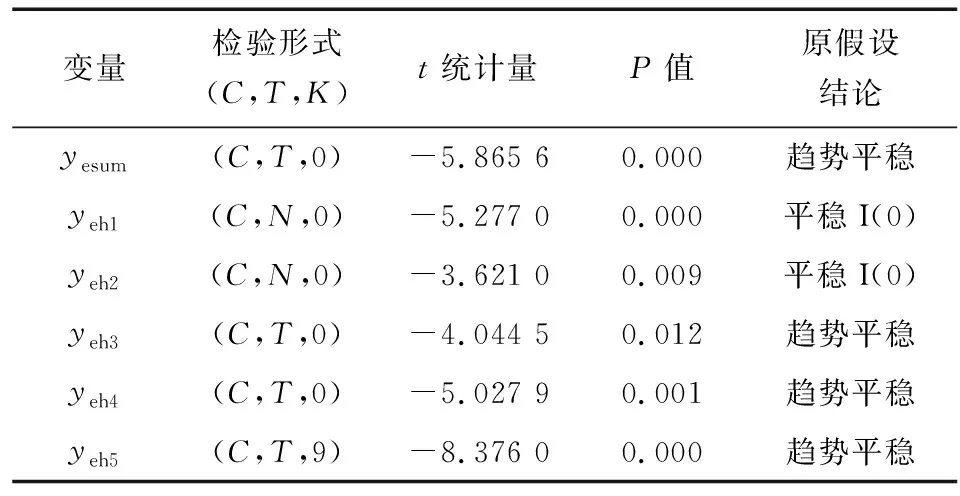
表2 ADF单位根Table 2 ADF unit root

由表2可知，高能耗产业的平稳性各不相同，部分为平稳时间序列；部分属于趋势平稳序列，其区别在于方程中是否含有时间趋势项。采用典型消除时间趋势项的差分方法，对趋势平稳的时间序列处理后再次检查该序列是否平稳，若平稳，则不需要进行Johansen协整检验。对表2中趋势平稳的变量进行差分处理后均为平稳序列。

3.2.2 Granger因果关系分析

为了反映产业用电量与经济指标之间的关系，在满足平稳性的基础上，构建各细分高能耗产业的VAR模型并进行Granger因果关系检验。变量选取：产业利润总额xprf、产业主营业务收入xinc、产业产量xprd。分析各细分高耗能产业用电数据与经济指标的因果关系，考虑到样本容量限制，本文选择最大滞后阶数为4，最终得到各个细分产业的因果关系，如表3所示。原假设指经济指标不能引起产业用电数据变化的Granger原因。

表3 格兰杰因果校验结果Table 3 Granger causality check result

由表3的检验结果表明：不同的高能耗产业的经济指标对于其用电量的Granger因果关系检验结果各不相同。化学原料和化学制品制造业、非金属矿物制品业都是由产业产量对用电量有Granger因果关系；而产业主营业务收入和利润总额是纺织业、有色金属冶炼和压延加工业用电量的Granger原因；黑色金属冶炼和压延加工业的经济指标数据对用电量都没有Granger因果关系。若特定的经济指标对具体产业的用电量具有Granger因果关系，则该经济指标的增长会引起该产业用电量的增长。

格兰杰因果关系检验的结论作为统计意义上的“格兰杰因果性”，不是真正意义上的因果关系，因此不能作为肯定或否定因果关系的根据。但是，其作为统计结论对于后续的用电量预测模型具有一定的参考价值。

3.2.3 高能耗产业月度用电量预测

在不同高能耗产业的Granger因果关系检验的基础上，将这些对产业用电量增长具有Granger因果关系的经济变量添加入自回归模型之中，构建最大滞后阶数为4的ARDL模型，选取赤池信息量准则(akaike information criterion，AIC)作为模型的信息准则，剔除不显著的变量后得到的回归结果如表4所示，其中，xeh1,prf、xeh4,inc、xeh4,prf、xeh5,prd分别表示纺织业的利润、有色金属工业的收入、有色金属行业的利润、非金属矿物制品业的产业产量。

表4 产业用电量回归估计结果Table 4 Regression estimation results of industrial electricity consumption

由表4可见，该地区高能耗产业的用电量合计受到该地区的纺织业、有色金属、非金属矿物制品业的某些具体经济指标的显著影响，如：纺织业当期的利润总额、有色金属加工业的滞后2期的主营业务收入和利润；非金属矿物制品业的产物水泥当月与上一季度的产量。地区某个产业的经济指标的增长，对于区域整体的高能耗产业的总用电量增长具有一定的影响作用。将经济指标与具体的产业现象相联系，进一步提升了模型的解释能力。

2016—2020年高能耗产业用电量ARDL模型的拟合结果如图4所示，本文构建的ARDL模型和自回归模型的拟合效果如图5所示。

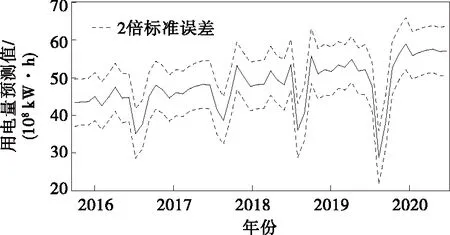
图4 ARDL模型拟合结果Figure 4 ARDL model fitting results

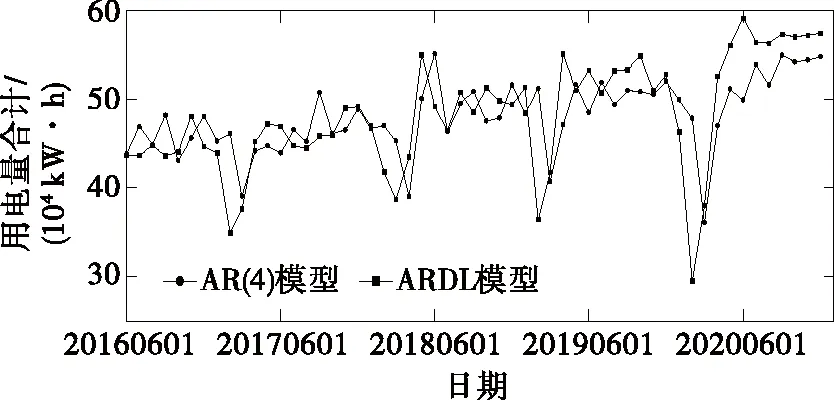
图5 中长期电量预测模型拟合效果Figure 5 Fitting diagram of mid-and long-term electricity forecasting model

由图4可知，与用电量实际值进行对比，模型的均方根误差(RMSE)为22 888.12 104kWh，平均绝对值误差(MAE)为17 166 104kWh，平均相对误差(MAPE)为3.628 8%，Theil不等系数(U)为0.023 74，偏差比为0，方差比为0.023 74，协方差比为0.976 25。从偏差比、方差比以及协方差比的结果看出，该模型对高能耗产业用电量的拟合效果较好。

由图5可得，ARDL模型的残差平方和为2.72×1010，回归标准差为26 385.24，而AR(4)模型的残差平方和为1.59×1011，回归标准差为55 850.97，均大于本文构建的ARDL模型，对比显示，ARDL模型对数据的拟合效果更好。

通过最新收集的2021年1—6月的该地区高耗能行业主要经济指标与用电量数据，验证模型中选取的经济指标是否与用电量存在长期均衡关系，模型的预测效果如图6所示,可见除了春节期间的相对误差约为10%外，其他月份都约为6%左右，整体的平均相对误差为6.84%，考虑新冠肺炎疫情对产业的冲击，该预测结果的精度处于可以接受的范围之内。

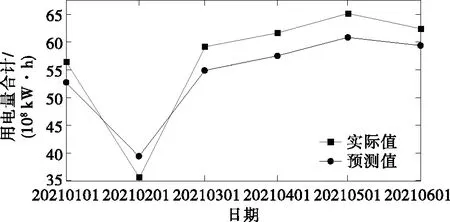
图6 高耗能行业用电量模型预测效果Figure 6 Prediction effect diagram of electricity consumption model for high energy-consuming industries

进一步分析预测结果可以发现，春节期间的预测值高于实际值；春节后的预测值都低于实际值。由于过往年份的预测结果中并没有显著的变化趋势，根据控制变量的原则，该现象与国内春节期间的高强度疫情防控策略相关；同时由于国内疫情得到有效控制，各个产业的用电需求在年后迅速反弹，导致年后实际值大于预测值。因此，对于预测模型的改进，还需结合产业政策、进出口贸易等多方面因素。

4 结语

本文研究细分高能耗产业的用电量与经济指标之间的关联分析，通过VAR模型和Granger因果关系挖掘影响细分产业用电量的经济变量，并在此基础上建立ARDL模型，对地区高能耗产业的用电量进行中长期用电预测。通过对地区产业的实际电力消费和经济数据进行方法验证，得出结论：

1)Granger因果关系检验和协整理论可以有效挖掘产业经济与用电的影响关联关系，对于含多元变量的模型分析有着重要的作用；将数理统计的理论应用于数据挖掘可以提高模型的解释性；2)Granger因果关系检验表明，不同细分产业发电量与各经济指标之间的关联性不同，具有关联性的产业经济指标的增长会促进该产业电力消费的增长；同时，考虑产业经济指标对于用电量预测模型的精度提升具有明显作用；3)基于ARDL和Granger因果关系的高能耗产业用电量预测模型，得到的预测与实际数据的相对误差较小；同时，研究细分产业的用电量影响因素对高能耗产业的整体用电量预测起到了较好的效果。