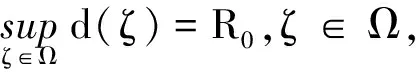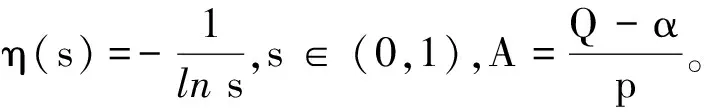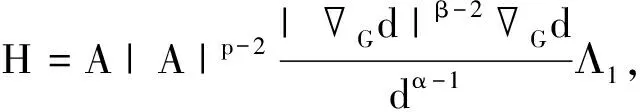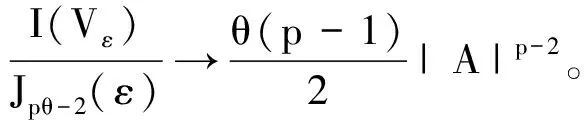Heisenberg型群上的一类带有余项的含权Hardy不等式
2023-01-13王胜军
王胜军
(青海师范大学 数学与统计学院, 青海 西宁 810008)

(1)

特别地,a=b=0,上式中的常数是最佳的。
1 预备知识
文献[6]提出Heisenberg型群,它是Heisenberg群的推广,是一类与亚椭圆问题相联系的Carnot群。作为满足Hörmander条件的一般向量场的重要模型,Heisenberg型群被更多学者广泛研究,并得到许多重要结果[7-10]。
设G是具有李代数G=V1⊕V2的一个2步Carnot群,且G被赋予内积<·,·>,定义映射J:V2→End(V1):
若∀ξ2∈V2,|ξ2|=1,映射J(ξ2):V1→V1是正交的,则称G是一个Heisenberg型群,简称H型群。
设X={X1,X2,…,Xm},Y={Y1,Y2,…,Yn}分别是V1,V2的基底,x=(x1,x2,…,xm)∈Rm,y=(y1,y2,…,yn)∈Rn分别是ξ1、ξ2在基底X={X1,X2,…,Xm},Y={Y1,Y2,…,Yn}下的坐标。通过文献[8],有

△pu=divG(|Gu|p-2Gu),
(2)
其中p>1。
设ζ=(x,y)∈G,在Heisenberg型群G上得到一个拟距离为
(3)
相应于(3)式的非迷向伸缩为
δτ(x,y)=(τx,τ2y),τ>0,(x,y)∈G。
(4)
与伸缩(4)相应,G的齐次维数是Q=m+2n。
通过(2)、(3)式直接计算知道
(5)
由文献[11]中的极坐标变换可以得到下列Heisenberg型群的极坐标变换(x1,x2,…,xm,y1,y2,…,yn)→(ρ,θ,θ1,…,θm-1,γ1,γ2,…,γn-1)。若u(x,y)=ψpv(d),Ω=BR2BR1,0≤R1 (6) 另外,定义中心在0∈G,半径为R的拟开球为BR(x,y)={(x,y)∈G|d(x,y) (7) 对于一个任意小的ε>0,定义下列函数: Vε(x,y)=φ(x,y)ωε, γ=pθ-2; (8) 引理1对于ε>0,下式成立: i)cε-1-γ≤Jγ(ε)≤Cε-1-γ,γ>-1; ii)Jγ(ε)=pε/(γ+1)Jγ+1(ε)+Oε(1), γ>-1; iii)Jγ(ε)=Oε(1),γ<-1。 (9) 易知, (10) (11) 同样,在(11)式中,利用(10)式证得i)左边不等式成立。 易知 (12) 从而,利用(12)式,得到 (γ+1)Jγ(ε)。 (13) 又由于 pεJγ+1(ε)。 (14) 通过(6)、(7)式知 (γ+1)Jγ(ε)=pεJγ+1(ε)+Oε(1)。 这样,ii)得证。 利用极坐标变换(6),有 (15) 当γ<-1时,通过(10)式可知(15)式是有限的,从而在(15)式两边取ε→0,证得iii)成立。 引理2∀ε→0,下式成立: |A|pJpθ(ε)+Oε(ε1-pθ)。 证明已知GVε(x,y)=φ(x,y)Gωε+ωεGφ,有 ΠA+ΠA1+ΠA2。 (16) 利用引理1的ii)知,ΠA1、ΠA2=Oε(1),ε→0。 结合(16)式有 |A|pJpθ(ε)≤ΠA-|A|pJpθ(ε)+Oε(1)= ΠB+Oε(1), (17) 其中 这样 ΠB≤ΠB1+ΠB2+ΠB3, (18) 其中 以下证明 ΠB1,ΠB3=Oε(1),ε→0。 (19) 在引理1的ii)中,取γ=-1+pθ,得到 ΠB1=-pA|A|p-2(εJpθ(ε)-θJpθ-1(ε))= -pA|A|p-2(εJpθ(ε)- εJpθ(ε)+Oε(1))=Oε(1)。 而 ΠB3≤cε3Jpθ(ε)+cJpθ-3(ε),ε>0。 由1 (20) 结合(17)~(20)式,得到引理2的i)。结合(17)、(20)式及引理2的i),有 |A|p-2Jpθ-2(ε)+Oε(1)≤ |A|pJpθ(ε)+Oε(ε1-pθ)。 因此,引理2的ii)成立。 (21) 特别地,在(21)式中取a=b=0,有下列带有余项的权Hardy不等式: (22)式中的常数是最佳的。 证明为方便证明(21)式成立,首先令 Λ1=Λ1(η)=1+ 从而当R足够大时,在Ω上有Λ0>0,Λ1>0。 (23) (24) (25) 利用(23)~(25)式,得 T1(s)-(p-1)AT2(s)T3(s)= (26) A|A|p-2d-α|Gd|β(pAΛ1+Λ2- (27) 通过(26)、(27)式,得到 (28) 又由于 即 (29) 将(28)式代入(29)式,利用(5)式,得到(21)式。 以下证明(22)式中常数的最佳性。 1)通过引理2的ii),得到 已知当ε→0时,有Jpθ(ε)→∞,所以当ε→0时,有 2)通过引理2的i),得到 综上,完成(22)式中常数的最佳性证明。

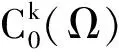
2 两个重要引理

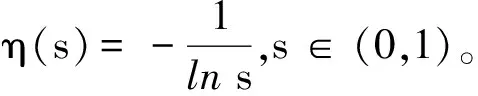
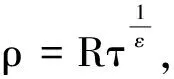
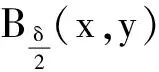


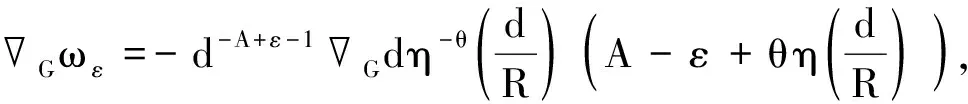
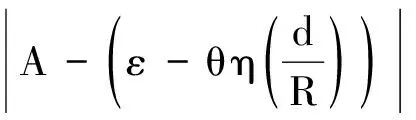
3 一类带有余项的含权Hardy不等式