平面三角形的径向平均体
2023-01-13印蕾钦陈艳妮
印蕾钦, 陈艳妮
(1 西南大学 数学与统计学院, 重庆 400715; 2 陕西师范大学 数学与统计学院,陕西 西安 710119)
在凸几何理论中, 研究凸体K的性质时, 其差分体DK和极投影体Π*K是重要的几何对象。差分体被广泛应用在数学物理的交叉学科和偏微分方程中,而投影体ΠK被广泛应用到Banach空间的局部理论、随机几何、组合数学等领域。因此,差分体DK和极投影体Π*K吸引了诸多学者研究[1-10],得到了很多优美的不等式。其中有两个著名的仿射不等式,其一为Rogers-Shephard不等式,即
其中V(K)为K的体积, 当且仅当K为单形时等号成立;另一个为逆向Petty投影不等式,也称为Zhang投影不等式,即
当且仅当K为单形时等号成立。
1998年,Gardner等[2]提出了凸体理论的新概念——p阶径向平均体(p>-1)。设K为Rn中的凸体,定义K的径向平均体RpK(p>-1)为
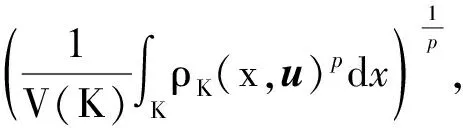
∀u∈Sn-1。
特别地,当p=0时
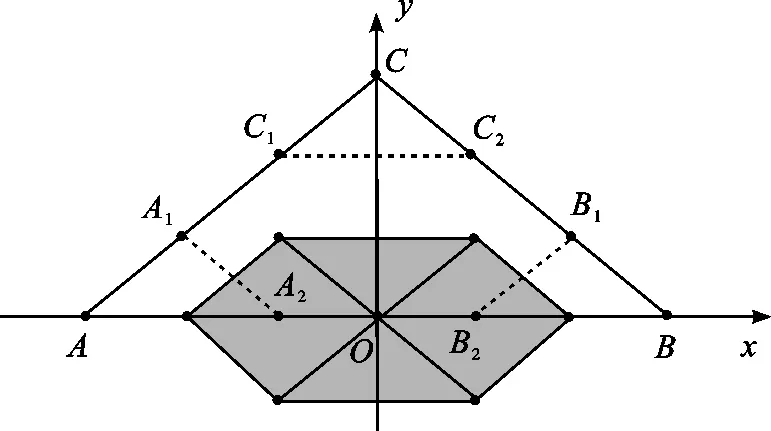
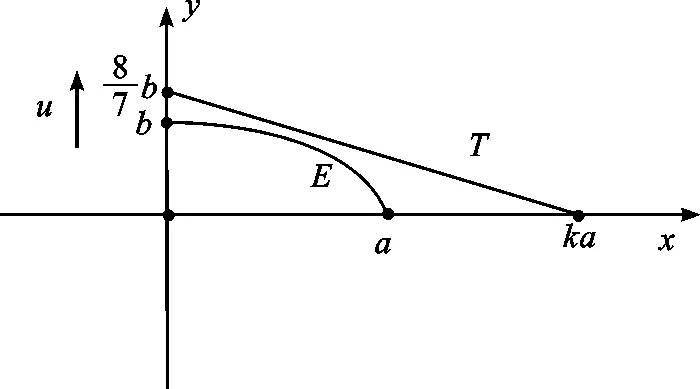
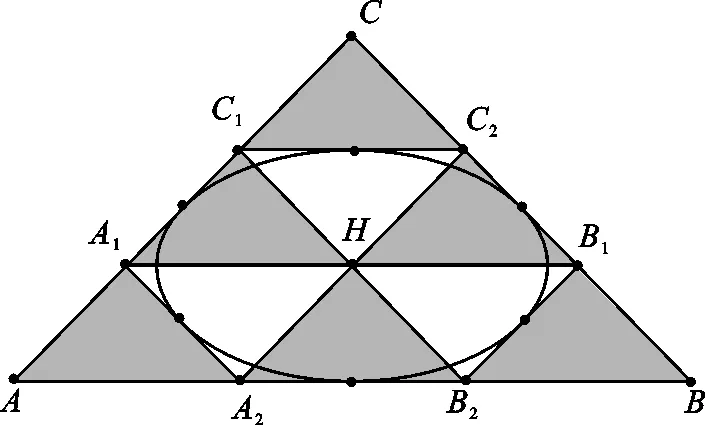
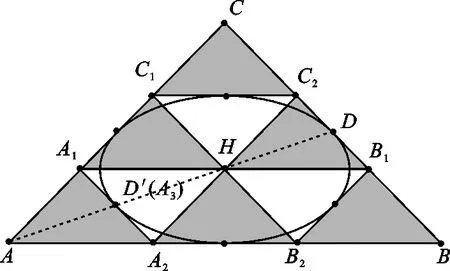
在文献[2]中,当-1 nnV(K)nV(Π*K), 文献[3]建立了p阶径向平均体的Brunn-Minkowski不等式。随后,倪建华等[4]得到在Rn中,单形K的p阶径向平均体与其差分体DK是位似的。2008年,文献[5]运用积分几何的方法研究了凸体K的p阶径向平均体的对偶均质积分,得出其与K弦幂积分的关系。 JK⊆RpK。 特别地,JK内切于R1K。 给定欧氏空间Rn,设K为Rn中的凸体,包含在K内部中体积最大的椭球称为John椭球,记为JK;Rn中的原点和单位球面分别记作o、Sn-1;u⊥为Rn中法向量为u的过原点的超平面;K|u⊥为凸体K在超平面u⊥的正交投影;lu为与u平行且过原点的直线;V(K)表示凸体K的体积。 设K为Rn中的凸体,定义径向函数 ρ(K,x,u)=max{λ≥0:x+λu∈K,x∈K, u∈Sn-1}, 也可简记为ρK(x,u)。特别地,x为原点时,简记为ρK(u)。 定义凸体K的p阶径向平均体[2]RpK(p>-1), ∀u∈Sn-1, (1) 其中 从而R∞K=DK,其中DK为K的差分体。特别地,当p=0时, 由定义可知,RpK是中心对称的。其中,当p≥0时,RpK仍是凸体[2]。 设u∈Sn-1,y∈u⊥,则有 XuK(y)=V1(K∩(lu+y))。 由此,定义SpK体[2]。当p≥-1,p≠0时, 当p>-1,p≠0时, (2) 若V(K)=1,则 R0K=e-1S0K。 由(1)和(2)式有,当p>-1,p≠0时, (3) 特别地,当n=2时,V(K)=S(K),其中S(K)为K的面积,以下简称为SK。 证明不妨设AB所在的直线为x轴,过C点作y轴, 如图1所示建立直角坐标系。并设点A、B和C的坐标分别为(a,0)、(b,0)、(0,c)。 图1 建立直角坐标系 由假设知,u与y轴平行。再由(3)式,则有 (4) 证明由文献[7]可知△ABC作X-ray对称化后仍为三角形。下令 △A′C′B′={x+tu:0≤t≤XuK(Q), x∈K|u⊥,Q=(x+lu)∩直线BC}。 以B′C′所在的直线为x轴,过点A′作y轴,如图2所示建立直角坐标系。 图2 K的X-ray对称化 设△A′C′B′为K′,B′C′边上的高为c,则由引理知 由K′的定义得 c=max{XuK(Q),Q=(x+lu)∩直线BC}= XuK(A), 为了证明平面三角形的一阶径向平均体为原点对称六边形,需要一些说明:设△ABC的AB所在的直线为x轴,过点C作y轴,建立直角坐标系。则由引理2得 (5) △ABC~△AA2A1。 (6) 图3 在顶点处对应的R1K 定理1平面三角形的一阶径向平均体为原点对称的六边形。 ρR1K(u)=|AA′|,A′=(A+lu)∩A1A2。 ρR1K(u)=|BB′|,B′=(B+lu)∩B1B2; ρR1K(u)=|CC′|,C′=(C+lu)∩C1C2。 因此,分别将△AA1A2、△BB1B2、CC1C2(如图3所示)中的点A、B和C平移至原点处后均为R1K的一部分,又由R1K是原点对称的,故R1K为原点对称的六边形。如图4所示, 即可得出结论。 图4 平面三角形的一阶径向平均体 将上一节中平面三角形的R1K推广到RpK,∀p>-1的情形, 并讨论相应的结论。设以AB所在的直线为x轴,过点C作y轴, 建立直角坐标系。 引理3设△ABC为平面上任意三角形,c为某一边的高,且该高的方向为u,则 p∈(-1,0)∪(0,+∞)。 证明设点A、B和C的坐标分别为(a,0)、(b,0)、(0,c),由(3)式可得 (7) 特别地,当p→∞时, ρR∞K(u)=ρDK(u)=c。 (8) p∈(-1,0)∪(0,+∞)。 引理5设任意三角形△ABC,当p>-1,p≠0时,满足 则有△ABC~△AA2A1。 △ABC~△B2BB1,△ABC~△C1C2C。 特别地,当p=0时,三角形仍满足 此时, 结论同样成立。 定理2平面三角形K的RpK(p>-1)是原点对称六边形。 根据Gardner等[2]的研究,提出:设K为Rn中的凸体,已知p≥0时,RpK为原点对称的凸体。当p>-1时,RpK是否也是原点对称的凸体? 由定理2得知,n=2时,三角形K的p阶径向平均体RpK(p>-1)仍是原点对称的凸体。 定理3设K、L为R2的凸体,且K⊂L,则R1K⊂R1L未必成立。 图5 凸体E、T 取定方向u与y轴平行。由(3)式得 且由引理1知 引理6设△ABC为K,SRpK为RpK的面积,则当p>-1时,SRpK为p的增函数。 事实上,对f(p)求导。当p≠0时, 而当p>-1时,f′(p)≥0。 定理4设椭圆JK为△ABC的John椭球,则当p≥1时, JK⊆RpK。 特别地,p=1时,JK内切于R1K。 证明只需证明p=1时,JK内切于R1K,再由引理6即得证。 由文献[8]可知,三角形的John椭球为Steiner内切椭圆,且与三角形三边的中点相切。取三角形重心H为原点,再由重心的性质和三角形相似得R1K为六边形A1A2B2B1C2C1(如图6所示)。 图6 在重心处的一阶径向平均体 为了便于计算,如图7所示,建立直角坐标系。由中线的性质,显然可得 图7 JK内切于R1K △AA1A2≌△HC2B1,△HC2B1≌△HA2A1。 (9) 不妨设A3=AD∩A1A2,D为BC边上的中点,D关于H对称的点为D′,由假设可知A3、D′共线。再由(9)式得,AA3=HD=HD′,则点A3与点D重合。从而,此椭圆与A1A2相切于A3。同理,椭圆与B1B2、C1C2相切,即JK内切于R1K。再由引理6,得证。 由引理3可得 R0K⊂R1K⊂R∞K=DK。 本文通过将平面三角形进行X-ray对称化, 给出了其径向平均体RpK为原点对称的六边形,并为解决相关文献提出的猜想提供了平面的例子。此外,得到了平面三角形的RpK与其John椭球的包含条件。今后,我们将考虑高维空间中单形的径向平均体与其John椭球间的包含关系。


1 预备知识


2 平面三角形的RpK
2.1 平面三角形的R1K

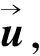



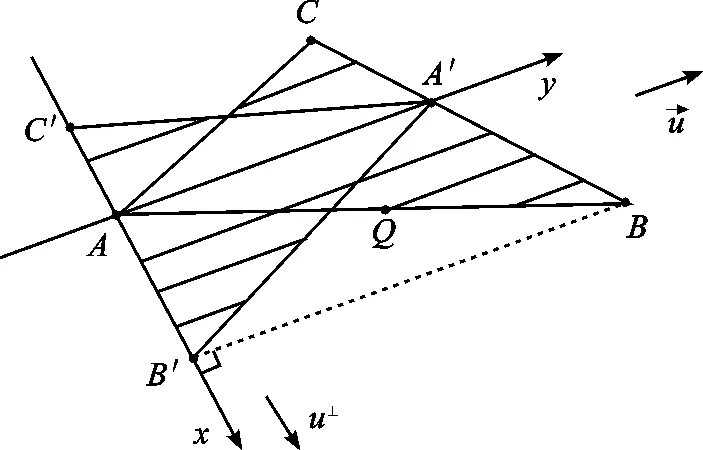

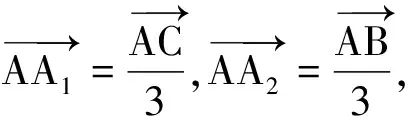


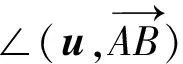
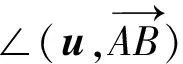
2.2 平面三角形的RpK




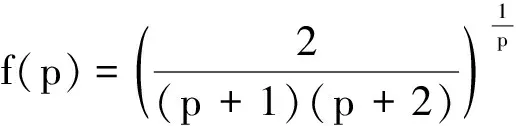
3 平面三角形的RpK的单调性
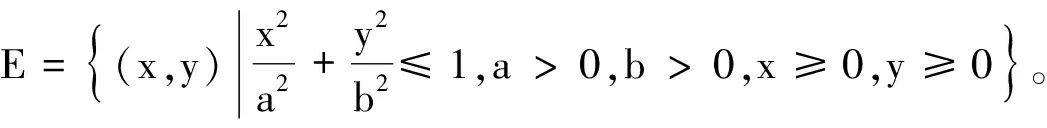


4 结语
