核心素养理念下指向学习能力培养的教学路径思考——以一道几何题的解决过程为例

应佳成

（浙江省杭州市富阳区教育发展研究中心）

在新课程理念下，发展数学核心素养是课程目标的集中体现，通过核心素养的培养进一步发展学习能力是《义务教育数学课程标准（2022年版）》（以下简称《标准》）的要求.能力的发展不能一蹴而就，需要在教师的启发、引导下，经历发现、体验、领悟等心理活动，将相应的问题内化到已有数学认知结构中，与已有数学认知结构相互作用、不断积累，才能实现从技能到能力的飞跃.

本文聚焦一道几何题的教学过程，通过层层递进的思考，沿着明暗交织的两条线索展开研究：以“解题技巧—原理分析—策略形成—建构生成”为明线完成教学活动，让学生在参与的过程中形成经验和方法；以“方法—联系—能力—素养”为暗线引导学生领悟数学的内在联系，提升思维水平.

学习材料：如图1，在△ABC中，DE∥BC，BE，CD交于点P.求证：直线AP平分BC和DE.

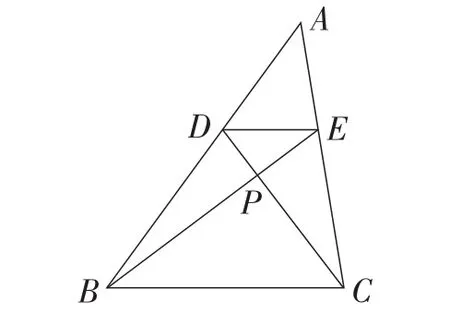
图1

一、解题技巧分析

材料问题的解决方法很多，主要集中于全等、相似、比例线段等方法，甚至可以用梅涅劳斯定理和塞瓦定理解题.但是从根本上看这些方法主要涉及全等与相似两类思路.全等与相似具有特殊与一般的关系，在解法上我们聚焦相似和比例线段相融合的思路，这是实际解题过程中最常采用的方法.

1.合理猜想，构建思路

首先，要指导学生构建解题思路，涉及的主要数学思想是转化与化归.综合学习材料的已知条件和结论不难发现，问题中涉及的图形间的关系并没有全部显性表达，需要学生“连接AP并延长，交BC于一点（Q）”，将“直线AP平分BC和DE”这个条件显性表达出来，并“过点P作MN∥DE∥BC”构造出与DE和BC平行的第三条平行线（如图2）.

图2

其次，执果索因，从结论倒推所需要的上位条件，我们不妨用图示法层层递进将内隐的思维过程显性构建出来，探寻解题思路如图3所示.

图3

2.演绎推理，准确表达

逆向使用思维框图，按照从因到果的过程完成演绎推理，问题即可得以解决.演绎推理能力是思维水平的直观显现，推理过程中容易出现表述繁杂、因果不清等现象，本质上是由于用“因为有A，所以有B”的论述方法解决具有复杂逻辑关系的问题时过程冗长、结构松散，可以引入逻辑推演符号“⇒”显示证明过程的逻辑结构，精炼证明过程，做到层次分明、简明扼要、清晰易懂.

这样就逻辑清晰地解决了MP=PN这一关键问题，接下来的论述就水到渠成了.

由此得到直线AP平分DE.同理，可得直线AP平分BC.问题得证.

从几何基本事实出发，有条理地运用分析法执果索因，探索、发现、设计论证思路，再由因导果完成演绎证明，这是解决几何问题的一般思路，在分析问题和解决问题的过程中发展学生的几何直观和推理能力.

二、基本原理挖掘

1.探究变化过程中的不变量

几何学习强调从运动变化的观点来研究图形、挖掘本质.在运动变化的过程中发现恒定不变的规律，并找出确定不变的根本原因，这是发现问题本质的一般思路.接下来我们沿着这样的思路挖掘材料的本质.

在上述问题解决的过程中，过点P添加平行线后，问题转化为对MP=PN的论证，而点P是梯形对角线的交点（如图4），由此引发思考，MP=PN是不是由梯形对角线交点决定的？

图4

事实上，MP=PN是对长度的刻画，而度量与面积密切相关，聚焦△DPB与△EPC这两个图形，发现无论梯形如何改变，由对角线相交构造出的△DPB与△EPC面积恒相等，这就是变化过程中的不变量.那么，决定三角形面积不变的关键要素是什么？由于左右两个三角形的“高度和”相等，因而依据面积公式发现PM与PN相等，也就是说点P的特殊位置是产生“直线AP平分BC和DE”这一结论的决定性因素.

基于图形面积间的关系发现线段长度间的关系是根本.以上分析证实了猜想“经过梯形对角线交点且平行于两底的平行线被交点平分”的正确性.在图4的基础上还可以进一步改变条件，如果平行线MN的位置是“动态”的，不经过梯形对角线的交点（如图5），可以得到MA=FN这个更为一般的结论.

图5

2.分析问题蕴含的数学原理

如果教学仅限于解决一道题，容易导致学习经验碎片化，能力提升空间有限.数学学习追求的是从特殊到一般不断逼近本质，指向公理、定理或者定义的数学原理分析是帮助学生理解问题本质、避免碎片化学习、积累学习经验、培养学习能力的关键环节.

事实上，以上问题解决的方法源于平行截割定理，但并不是直接使用该定理.学生也许会产生疑惑，熟悉的平行截割定理为什么在此题中使用起来不顺畅？接下来层层递进指向本质.

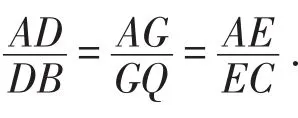
图6

第二步，将所获结论一般化.一组直线束在一条直线上截得相等的线段，在该直线的平行直线上也截得相等的线段.

第三步，进一步推广.一组直线束截两条平行线，所得的对应线段成比例.

第四步，总结.如果一组直线束被两条平行线所截，不仅直线束被平行线截得的线段间存在比例关系，平行线被直线束截得的线段间也存在比例关系.这正是学习材料的解决基础，深度剖析的过程可以提升学生的理解层次，是能力培养的重要过程.

以上分析推广了定理、解释了MP=PN的根本原因，还基于运动变化的视角总结出更具一般性的结论，使得课堂生成远远超出材料本身，将学生的思维水平推上新高度.

三、策略形成指导

学习材料中题干的条件少之又少，说明材料内涵丰富、拓展性好、结论具有一般性.从方法论的视角看，具有一般性的结论往往可以在不同的领域间产生广泛的联系.

1.在数学间相互表征

学习的过程是建立联系的过程，用代数关系将一个几何问题中蕴含的数量关系表达出来是数学逻辑发展的需要，是培养几何与代数相互表征能力的过程，广义上看是培养数形结合思想的重要过程.

至此，在材料中挖掘出基本几何结构与代数结构的相互表征，其关系如图7所示.

图7

2.数学与其他学科的联系

图8

由于数学内容间、数学与其他学科间的关联往往比较隐蔽，学生不容易发现，因此策略形成阶段需要突出教师的指导作用，指导学生找出新、旧内容在一般原理中的一致性，指导他们将具体问题归纳为一般原理，从一般原理的高度去认识问题，使思维方式具有广泛的迁移性，形成能力.

四、建构生成观念

数学学科的特点是不同分支有一定的独立性，但同时又有内在的紧密联系，建立这种联系是数学教学的重要任务.在上述问题解决的过程中，存在一个不可回避的问题：尽管学习材料的结论非常优美，但是平行截割定理与相似三角形原理交替使用，思考和论证都比较烦琐.与优美的结论相比，现有的知识范畴已经无法帮助学生做出更简洁的论证方法，构建更高层面的知识框架便成为需要.

中学几何中的某些问题可以归结为射影几何问题.在射影几何视角下，由于经过同一个无穷远点的直线都平行，因此平面几何中心射影（直线束）和平行射影（平行线）两者就可以得到统一，平行射影可以看作经过无穷远点的中心投影，这样恰当地利用完全四点形交比定理的无穷远特例可以快速解决问题，降低问题解决的难度，优化证明思路，使过程清晰、简洁，可以让学生领略构建新知识体系系统化解决问题的魅力.

1.概念重构

如图9，设A，B，C，D是射影直线l上的4个不同点，如果（ABCD）=-1，则称A，B，C，D为一个调和点列，或者说点A，B被点C，D调和分割.特别地，若点D是一个无穷远点（如图10），则（ABCD）=（ABC）=-1，即点C为线段AB的中点.

图9

图10

2.性质定理

设A，B，C，D是射影平面上的4个不同点，满足任意三点不共线，AB交CD于点F，AD交BC于点H，AC交FH于点G，DB交FH于点E，AC交DB于点K（如图11），则（FHGE）=（DBKE）=（ACKG）=-1.

图11

3.解决问题

图12

4.学习心理建构

此题重新论证完成后，需要帮助学生至少在两个方面建立内心体验：其一，用现有知识将需要反复论证的问题换一个视角，提升思考维度，问题则可以得到轻松解决，在文章第一部分中提到的各种解题思路，诸如平行截割定理、相似原理、特殊的梅涅劳斯定理、塞瓦定理等都可以在射影变换性质下（交比定理）得到统一的解释；其二，对新知识体系的研究还是沿着熟悉的“概念—表示—性质—判定—应用”的路径展开，并没有脱离认识问题的基本路径，激发学生产生积极学习的心态，不会因为未知而产生畏惧心理，愿意尝试用更高维度的视角解决现有的问题，理解学会学习才是真正面向未来的能力.

五、总结

1.站稳“四基”，发展“四能”

几何教学需要站稳“四基”，不能好高骛远.在一线调研中发现，逻辑关系不清晰导致的学习问题仍然存在，教师应该基于几何直观，从几何基本事实出发，步步有据，用好数学语言，着力抽象能力、推理能力的发展，培养学生利用几何知识分析和解决问题的能力.学生能力的培养、思想方法的形成并非一朝一夕便可以完成的，而是需要点点滴滴的积累，在学生活动的过程中逐渐渗透，积累到一定程度可以产生质的飞跃，形成数学观念.

2.发展能力，学会学习

能力是概括化、系统化的知识技能.数学能力是在获得数学知识、数学技能的基础上，通过广泛迁移不断概括化、系统化而实现的.数学学习的意义，是在已知的数学对象和数学关系与未知的数学对象和数学关系间建立联系，解决问题.教师需要创造机会，让学生体验到问题解决是推动数学发展的动力，数学在不断自洽的过程中向前发展，这样的体验可以激发学生不断探究数学奥秘的欲望，从而发展能力，培育核心素养.例如，本文材料的深度挖掘，可以扩大眼界，让学生知道在欧氏几何以外还有一个广阔的几何学的新天地.中学生正处于思维最为活跃的年龄，尝试把学习放在一个更广阔的背景下来思考，所获得的对数学的总的认识，对培养和提高学生的学习兴趣可以起到长久的作用.这种指导虽然是抽象的，但是对培养学生的辩证思维具有深刻意义.