海底混凝土配重层单层管受落物冲击损伤因素分析

田博文，贾鲁生，余 杨，黄 俊，张春迎，余建星

1.天津大学，天津 300072

2.中海油研究总院有限责任公司，北京 100028

输送油气资源的海底管道距离较长，在运行过程中容易受到落物撞击而产生凹坑，导致局部椭圆度变大，易发生压溃和屈曲传播。郭振邦等[1]计算了锚链撞击海底管道的概率，并依据算例着重评估了偶然性载荷引发的风险。

众多学者进行了大量实验，推导出了几个常用的经验公式，Bai Yong[2]和Furnes[3]等分别推导出了不同的理论公式，描述了管道受撞击处凹坑深度与撞击力之间的关系。Jones N等[4-5]对两端夹紧条件下的缩比尺管道进行了碰撞试验，研究了冲击悬跨管道不同位置点对管道凹坑变形的影响，推导出一个近似的动力学公式。Shen等[6]使用准静态分析方法来预测管道受落物撞击后的响应和失效，采用了最大应变准则和估计塑性铰长度的经验公式，得到了撞击能量与管道应变之间的关系。

随着有限元软件的发展，数值模拟被广泛应用于海底管道受冲击载荷作用的损伤分析。Zeinoddini等[7-9]研究了轴向预加载作用下的管道在受到冲击载荷作用下的力学性能，采用非线性有限元隐式时域动态方法对冲击试验进行了数值模拟，研究了不同边界条件对管道受撞击的影响。

Wang Yu等[10]结合落锤冲击试验和LS-DYNA数值模拟，研究了超轻水泥填充管中复合结构的横向冲击性能。Daniel等[11]使用了四分之一有限元模型进行建模，能够在减小计算量的基础上，保证计算精度，推导出了在给定载荷下管道产生永久凹坑深度的公式。王希清等[12]论述了抛锚作业对海底管道的影响，计算了锚撞击海底管道概率，提出了控制风险源的办法。Andrew Palmer等[13]研究了新建海底管道落在现役运行管道的碰撞情况，并进行了全尺寸带有配重层的海底管道的碰撞实验，研究了管道椭圆化、混凝土破碎等能量吸收占比，从能量角度对海底管道碰撞过程进行了分析，为研究管道碰撞保护提供了新的思路。

本文针对带有配重层的单层管，其钢筋混凝土配重层选取分布式模型，钢筋与混凝土之间采用嵌入式约束模拟其黏结作用，研究了混凝土厚度、管道径厚比、落物能量、落物形状、管道埋置深度和管道所受压力等敏感性因素，分析了管道凹坑变形和各部分之间吸收能量的关系，为管道安全防护提供了一定的参考。

1 数值模型及碰撞分析

1.1 模型验证

管道模型具有对称性的特征且落物撞击位置为管道的对称面，本章所述的管道和落物均选取1/4模型进行简化计算，模型及边界条件如图1所示。管道、落物、刚性垫板的对称面均采用对称面约束，其中落物只允许Y方向位移，管道非对称面一端施加固定约束，管道下方刚性垫板施加固定约束。

图1 模型及边界条件

通过全尺寸管道碰撞实验，验证了建立模型方式的准确性。依托天津大学深水结构实验室，进行了全尺寸管道碰撞实验[14]，实验中落物选用质量为42.55 kg和61.70 kg的法兰，落物高度分别为6、8、10 m，其碰撞实验示意如图2所示，高速摄像机可以对法兰下落过程进行拍摄，并在电脑上输出法兰的速度与加速度等数据，从而为撞击能量的计算提供准确的基础数据。

图2 管道碰撞实验示意

数值仿真与实验数据对比如表1所示。从表中可以看出，使用有限元软件计算得到的结果与实验结果十分接近，凹坑深度和附加椭圆度最大相对误差分别为5.20%和5.48%，均小于6%，在允许范围内，验证了模型的准确性。

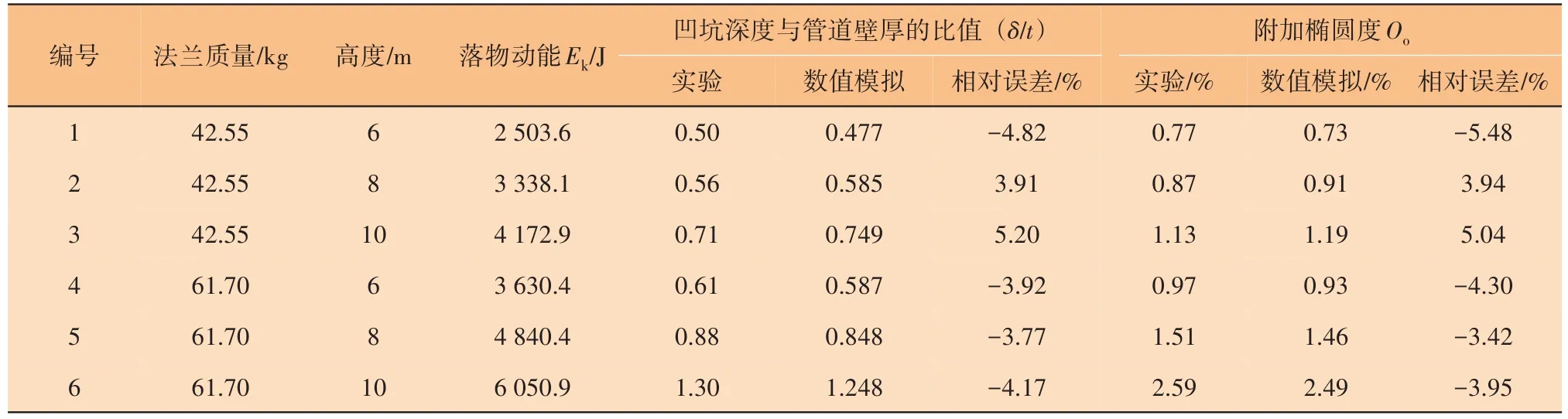
表1 数值仿真与实验数据对比

1.2 模型介绍

本节选取的研究对象为带混凝土配重层的单层管，其结构如图3所示。图中管道外面有一层钢筋混凝土包被，可以为管道提供一定的负浮力，并且在管道受到落物冲击载荷作用时发挥一定的保护作用。模型主要分为三个部分，分别为落物、带钢筋混凝土配重层的单层管和海床土体。落物选取球形落物，单层管道由钢筋混凝土配重层和管道组成，海床土体选取长方体土块。

图3 带混凝土配重层的单层管

本节的钢筋混凝土模型采用分离式模型，其能够充分考虑钢筋和混凝土之间的黏结和滑移作用，且适用于三维结构分析，与实际情况较为相符。混凝土和钢筋分别采用C3D8R单元和T3D2桁架单元，使用嵌入式约束Embedded将钢筋嵌入混凝土。

钢筋采用的应力-应变模型为强化的二折线模型，无刚度退化。本文中纵筋为HRB335钢筋，屈服强度为335 MPa；箍筋为HPB235钢筋，屈服强度为235 MPa，泊松比均为0.3。

混凝土本构关系采用塑性损伤模型CDP（Concrete Damaged Plasticity），假设拉伸开裂和压缩压碎为混凝土材料失效的主要机理，其可模拟混凝土是连续的，基于塑性损伤的情况。

为保证计算的准确性，需要选择正确的边界载荷条件，本节选取经本文1.1验证过的1/4模型，边界条件如图4所示。管道、土体、落物的对称面均采用对称面约束，其中落物只允许Y方向位移，管道非对称面一端施加固定约束，土体底端施加固定约束，并在端面限制法向方向的位移。

图4 模型边界条件

1.3 碰撞过程分析

为了研究受冲击载荷作用时混凝土配重层对海底管道的保护作用，选取尺寸相同的单层管和钢筋混凝土配重层单层管进行碰撞对比分析。本节管道的尺寸和材料属性如表2所示，参照DNVOS-F101规范[15]，混凝土层厚度为40 mm，落物为600 kg的球形落物，撞击速度为5 m/s，落物动能为7.5 kJ。海床土体选取2 m×2 m×3 m的土块，将管道平放于土体之上。

表2 管道尺寸和材料属性

混凝土配重层单层管受冲击载荷需要经过钢筋混凝土配重层传递至管道，此时管道可以视为无限长梁[16]。混凝土配重层单层管受冲击载荷作用的动态过程如图5、图6所示。

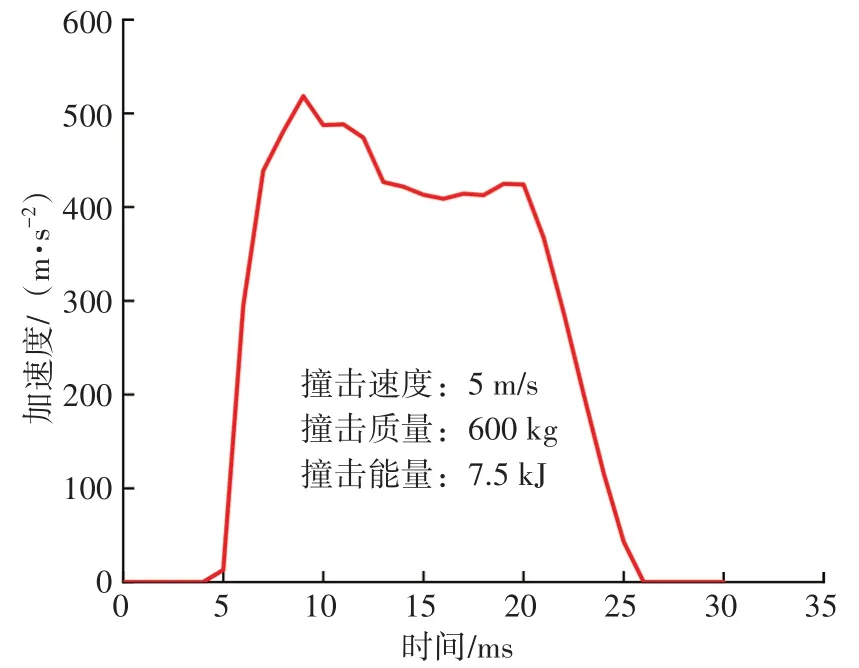
图5 落物加速度时程曲线

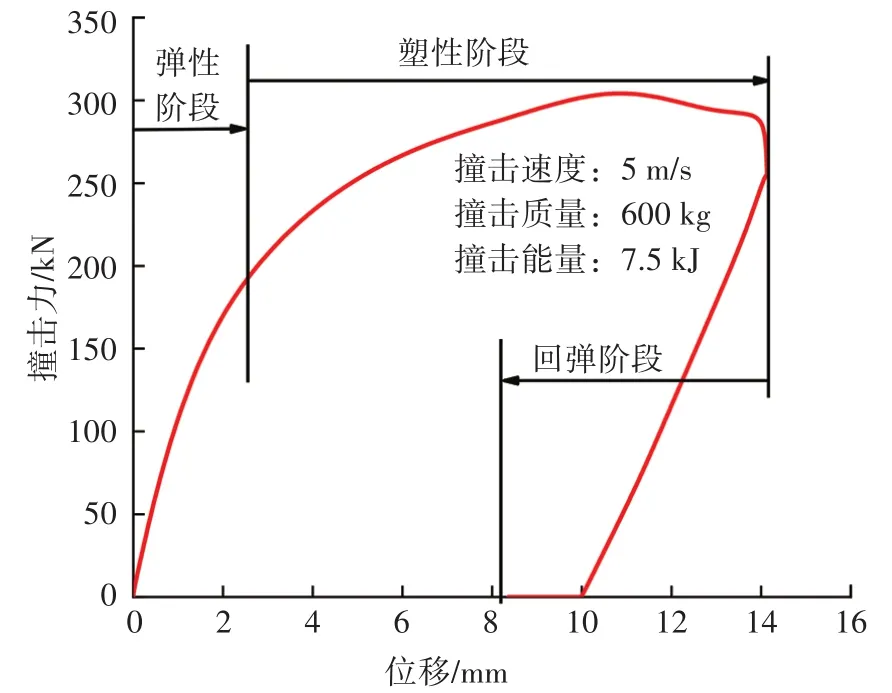
图6 撞击力-位移曲线

由图可见，撞击过程持续时间约为20 ms，最大的加速度为518.28 m/s2。碰撞过程中落物首先与钢筋混凝土配重层接触，在碰撞过程中，部分混凝土配重层发生破碎而失效。碰撞过程大致可分为3个阶段，分别为弹性阶段、塑性阶段和回弹阶段，撞击过程中最大撞击力为310.97 kN。

1.4 碰撞对比分析

混凝土配重层对管道有一定的保护作用，建立单层管模型，将二者的计算结果进行对比分析，研究混凝土配重层的保护作用。

混凝土配重层在落物冲击载荷作用下，会吸收部分撞击能量，减小对管道的冲击，两种管道受落物冲击作用吸收能量情况如图7、图8所示。与单层管相比，混凝土配重层单层管对冲击能量的吸收占比大大减小，其吸收的最大内能占动能的53.9%。与混凝土配重层单层管相比，单层管碰撞时间比较长，这是因为管道发生弹性变形时吸能能力大于钢筋混凝土配重层发生弹性变形时吸能能力，故其弹性阶段与回弹阶段时间均较长。

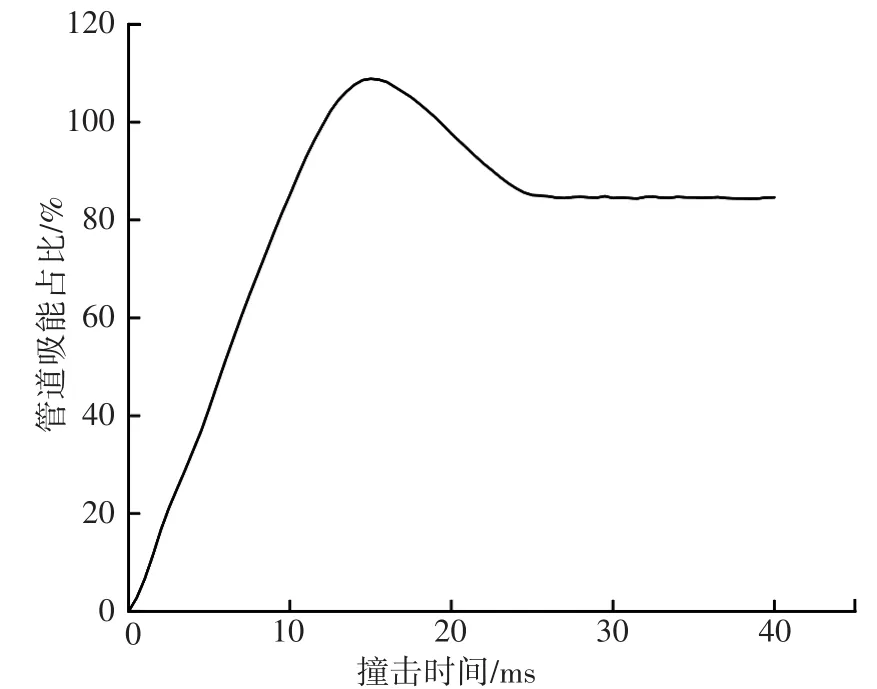
图7 单层管吸能曲线

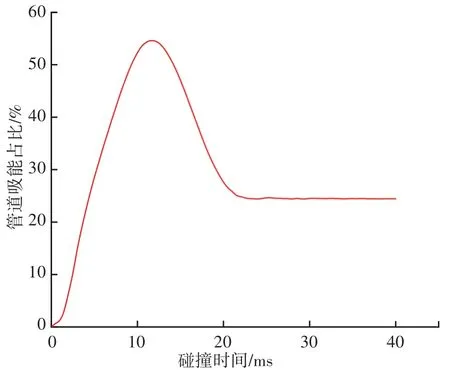
图8 带混凝土配重层单层管吸能曲线

两种管道撞击截面处凹坑深度随时间变化的关系曲线如图9、图10所示。单层管受碰撞产生的凹坑深度最大值为36.53 mm，带混凝土配重层单层管产生凹坑深度最大值为14.25 mm。可以看出，混凝土配重层的存在可以大大降低海底管道受落物冲击载荷作用过程中产生的凹坑深度最大值，提高了海底管道安全运行的能力。

图9 单层管凹坑深度

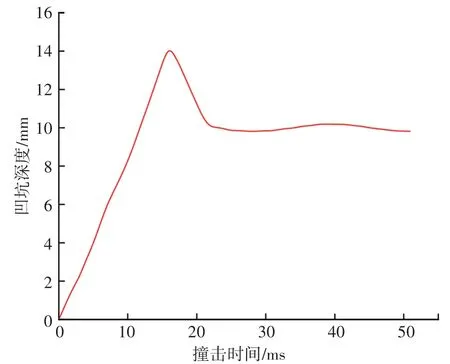
图10 带混凝土配重层单层管凹坑深度

结合图7～图10可以看出，凹坑深度随时间变化的趋势与吸收能量的趋势相似，可以分为以下三个阶段。

第一个阶段为凹坑深度逐渐加大的过程，此时落物的速度逐渐减小为0，落物动能逐渐转化为管道内能。

第二个阶段为凹坑深度逐渐减小的回弹阶段，此时管道发生弹性回复，此阶段管道的内能转化为落物的动能，落物开始向上运动至与管道脱离。

第三个阶段凹坑深度趋于稳定，此时落物与管道完全脱离，完成碰撞。

2 损伤因素分析

2.1 撞击能量

落物质量和落物速度是影响落物动能的重要因素，本节选取的落物质量为200、400、600、800、1 000 kg，选取的落物速度为3、4、6、7 m/s，研究速度对撞击损伤程度的影响。

管道凹坑深度-速度变化曲线如图11所示。可以看出：在相同质量下，随着速度的增加，管道的凹坑深度在不断增大，而且增大的趋势在逐渐加快。以速度为3 m/s的600 kg的落物为基准，当其速度变为4、5、6、7 m/s时，其凹坑深度分别增加了132%、339%、629%和967%，增长速率在逐渐加快，与质量相比，速度对于凹坑深度的影响更为明显，这是因为在动能的表达式中，速度对动能的影响是二次方的关系。

图11 管道凹坑深度-速度变化曲线

以落物速度为5 m/s为例，管道受落物撞击的截面变形情况如图12所示。从该图可以看出：随着落物质量的不断增加，管道的变形也逐渐变大，凹坑深度增长速率逐渐加快。

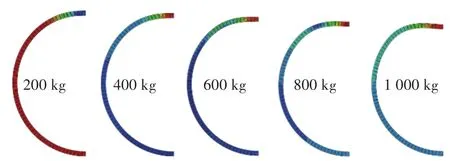
图12 管道受落物撞击后截面变形情况

以600 kg落物为研究对象，距管中截面30 cm范围内管道的变形如图13所示。从该图可以看出：除了最大凹坑深度不同之外，离撞击位置越远的管道部分，凹坑深度越小；随着撞击速度的增大，距管中截面30 cm范围内，凹坑深度均呈现增大的趋势，在撞击位置处凹坑之间的深度差别达到最大值。随着撞击速度的增加，变形深度的增加十分明显。

图13 距管中截面距离与变形深度关系曲线

2.2 落物形状

2.2.1 圆锥形落物

本节选取质量均为600 kg的圆锥形落物进行研究，其圆锥角分别为30°、45°、60°和75°，圆锥形落物撞击产生的凹坑深度和管道最大Mises应力与速度的关系如图14所示。

图14 不同圆锥角撞击产生的凹坑深度和最大Mises应力

从图14中可看出：凹坑深度和管道最大Mises应力随着速度增加而逐渐增大；在相同速度下，凹坑深度和管道最大Mises应力随圆锥角增大而逐渐增大。

2.2.2 立方体、圆柱和棱形落物

本节选取600 kg的立方体、圆柱形和棱形落物进行研究，落物的撞击速度分别选取3、4、5、6、7 m/s，立方体、圆柱形和棱形落物撞击产生的凹坑深度和管道最大Mises应力与撞击速度的关系如图15所示。

图15不同形状落物撞击产生的凹坑深度和最大Mises应力

从图15可以看出：凹坑深度和管道最大Mises应力随着速度增加而逐渐增大；在相同速度下，圆柱形落物凹坑深度和管道最大Mises应力最大。

2.3 管道埋深

本节选取的埋置深度分别为0.325、0.650、0.975、1.300、1.625 m，落物选取600 kg的球形落物，撞击速度分别选取3、4、5、6、7 m/s。随着管道埋置深度的变化，撞击管道与土体吸收能量的比例会发生变化，速度为5 m/s的600 kg球形落物管道与土体之间的吸能占比如图16所示。

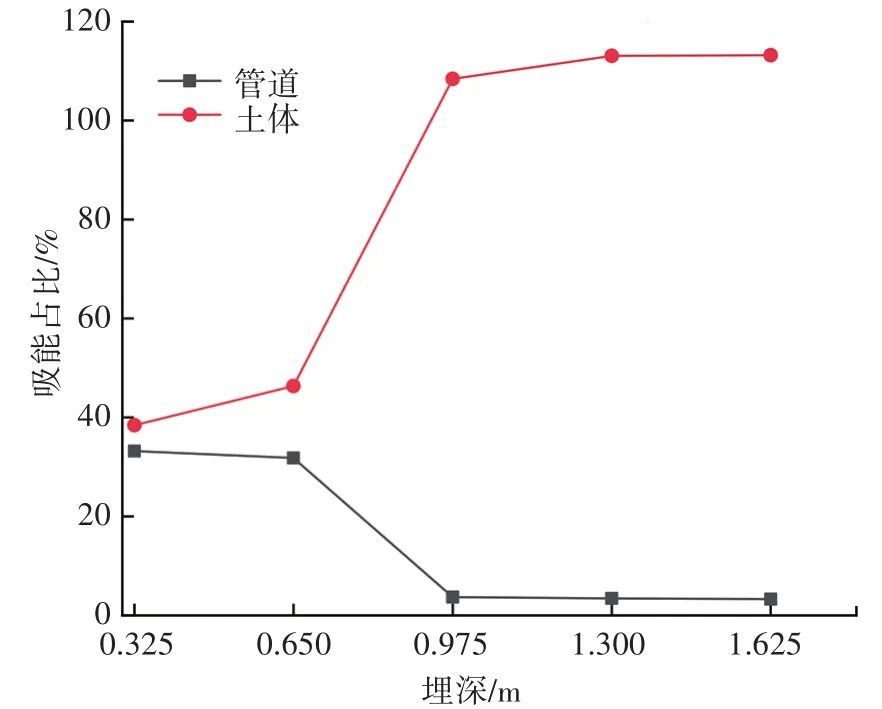
图16 不同埋置深度能量吸收关系

从图16中可以看出，随着埋置深度的增加，管道吸收的能量迅速降低。

管道的凹坑深度和最大Mises应力与埋置深度的关系如图17所示。从该图可以看出：管道的凹坑深度和最大Mises应力随着埋置深度的增加而迅速减小。

图17 不同埋深下管道凹坑深度和最大Mises应力

2.4 运行压力

海底管道所受的压力分为内压和外压，其中内压来源于管道运输的高温高压油气资源，外压来源于外部水压，管道受到的内外压之间可“抵消”。考虑海底管道在运行过程中受到的压力情况，本节选取-2 MPa（负值表示内压大于外压）、-1 MPa、0 MPa、1 MPa（正值表示外压大于内压）、2 MPa、3 MPa、4 MPa、5 MPa、6 MPa和7 MPa的情况，落物选取600 kg球形落物，落物速度分别选取3、4、5、6、7 m/s。

管道凹坑深度与运行压力的关系如图18所示。从该图可以看出：管道内压的存在（压力为负值时）可以减小管道凹坑深度，而外压（压力为正值时）会增大管道凹坑深度。

图18 不同运行压力下管道凹坑深度

2.5 管道径厚比

在相同的直径下，不同径厚比（D/t）的管道对应的吸收能量占动能的比例如图19所示。从图19（a）可以看出：带有配重层的管道吸收的能量随着管道径厚比的增大而逐渐增大；在同一径厚比条件下，随着撞击速度的增加，管道吸收能量的占比逐渐增加；径厚比对管道吸能占比增长率的变化有一定的影响，随着径厚比的减小，能量吸收占比曲线的斜率逐渐增大，说明管道吸能占比增长速率在逐渐变大。从图19（b）可以看出：在相同的撞击速度作用下，管道径厚比越大，管道产生的凹坑深度越大。

图19 不同径厚比下管道吸能占比和凹坑深度

2.6 混凝土厚度

本节分别选取20、30、50、60 mm厚度的混凝土配重层进行分析，不同混凝土配重层厚度下管道凹坑深度与速度的关系曲线如图20所示。

图20 不同混凝土厚度下凹坑深度与速度的关系曲线

从图20可以看出：以相同的速度撞击管道，随着混凝土配重层厚度的增加，管道的凹坑深度逐渐减小；随着混凝土配重层厚度的减小，凹坑深度的增加呈现出上升的趋势。这说明混凝土配重层厚度减小导致管道安全性下降是必须考虑的重点因素，在设计管道时应对混凝土配重层的厚度进行重点考虑。

3 结论

（1）开发的数值模型与实验吻合，误差小于6%；层间黏结和土体模型可提高模拟结果的准确性；在ABAQUS软件后处理过程中，可以显示撞击过程中管道的应力应变、系统的能量转化情况和海床土体变形，能直观准确描述整个撞击过程。

（2）通过与单层管受冲击载荷作用进行对比，分析了带混凝土配重层单层管在能量吸收、凹坑深度、最大Mises应力等方面的不同之处，并进行定量分析，明确不同因素使管道压溃压力下降的百分比和下降/上升趋势。

（3）对钢筋混凝土配重层单层管进行碰撞分析可知，配重层可以对管道起到很好的保护作用；撞击能量、落物形状、管道埋深、运行压力和土体参数等外部因素对管道受冲击载荷损伤有一定影响，其中撞击能量越大，管道损伤越严重；管道的自身参数对管道受冲击载荷损伤有重要影响，减小管道径厚比或增大混凝土厚度，均可降低管道的损伤程度。