基于飞行数据的涡扇发动机性能模型修正技术

2023-01-13秦海勤任立坤李边疆

燃气轮机技术 2022年4期

秦海勤，赵杰，任立坤，李边疆

(海军航空大学青岛校区，山东青岛 266041)

海军用航空发动机尤其是舰载机发动机长期工作在高温、高湿、高盐雾的恶劣环境下，相较陆基发动机而言性能衰退更加严重。发动机性能衰退可能会造成舰载机滑跑距离不够,引起飞机坠海等严重事故。因此为保证飞行安全，有必要开展海军用航空发动机的性能监测技术研究[1-3]。性能监测的前提是能够建立高精度的性能计算模型。为此国内外学者开展了大量研究。德国的Kurzke博士开发了Gasturb仿真软件[4]；NASA与美国国防部开展了“推进系统数值仿真”(numerical propulsion system simulation, NPSS)技术研究，开发了高精度、多学科的NPSS软件；欧盟也相应开展了VIVACE-ECP计划，研发了高保真度、多学科、多系统的PROOSIS建模平台。国内在发动机建模领域研究起步较晚，但也已取得了一定进展[5-7]。

目前航空发动机整机建模技术已相对成熟，但在实际使用过程中，受装配、制造公差等因素的影响，建立的发动机基准模型与发动机实际性能之间存在一定差异，因此通常须要修正部件特性对基准模型进行修正。台架试车装配有大量传感器，能够满足发动机模型修正系数计算的要求。因此，目前大多数模型基于台架数据开展部件特性修正[8-9]。但基于台架数据的修正模型很难真正应用于部队的性能退化评估和性能状态监测，这是因为一方面台架数据是发动机“裸机”状态下的数据，没有考虑装机后发动机与进气道等的飞机与发动机匹配问题，导致虽然台架数据修正的模型计算精度较高，但用于实际飞行数据时误差较大；另一方面，随使用时间的增加，发动机的性能会出现衰退，基于台架数据的修正无法考虑这种衰退情况。因此为使所建立模型能够真正应用于部队对发动机的性能退化评估和性能状态监测，应该用实际的飞行数据对模型进行修正。但受限于安装空间和质量等因素，装机状态下发动机安装的传感器数量有限，在进行模型修正时，可用飞行数据的数量远小于发动机修正系数数量，修正系数求解方程成为欠定方程。

针对上述情况，本文提出一种基于飞行数据的发动机模型修正方法，以某军用小涵道比涡扇发动机为研究对象，将发动机慢车以上转速分为4个区域，在每个区域内假设修正系数不变，采用多工作点分析(multiple operating points analysis, MOPA)方法[10]，利用多个稳态测量点的数据拓展发动机性能模型修正系数求解方程组，解决修正系数求解时的欠定问题，并使用一种自适应差分进化算法[11]求解上述方程组。在对发动机稳态模型修正的基础上，综合考虑转子惯性、容积惯性、热惯性对发动机瞬态的影响，进一步建立发动机的过渡态模型，并对加减速过程进行仿真。通过与实际飞行数据对比，稳态点计算误差在1.70%以内，过渡态计算误差在5.5%以内，能够满足工程精度要求，可为部队开展发动机性能退化评估和性能状态监测提供技术支撑。

1 发动机建模与修正

1.1 研究对象

本文的研究对象为某型军用小涵道比涡扇发动机，发动机的主要部件有二级轴流风扇、八级轴流高压压气机、环形燃烧室、一级高压涡轮、一级低压涡轮、外涵道、混合室、尾喷管等。该型发动机通过全权限电子调节器进行控制，传感器数量相对较多。

1.2 稳态模型的建立与修正

为减轻监控工作量，可利用现有的商业软件建立发动机基准模型[12]。PROOSIS软件是一款具有高保真度、可进行多学科联合仿真的发动机建模软件。该软件提供了友好的交互式图形化仿真界面，可根据建模对象的特点快速搭建性能仿真模型。因此本文利用PROOSIS软件建立了该型发动机变比热的基准稳态模型，如图1所示，模型包括了进气道、风扇、压气机、燃烧室、高压涡轮、低压涡轮、混合室、尾喷管和引气等模块。

图1 涡扇发动机部件级模型截面图

通常航空发动机非线性气动热力学模型可以表达如下：

(1)

z(t)=g(x(t),u(t))

(2)

式中：x为发动机状态向量；u是发动机输入向量；z是发动机测量参数向量。

发动机的整机性能由各部件性能决定，而部件性能主要取决于部件特性图是否能真实反映部件的工作过程，即特性图的质量。因此为得到准确的仿真计算结果，通常的做法是对特性图进行缩放，使模型与发动机实际工作状态相吻合。本文定义发动机部件流量和效率修正系数分别为：

(3)

(4)

式中：W为部件换算流量；η为部件效率；下标real和cal分别表示为真实发动机数据和模型计算数据。

由转动部件(风扇、低压压气机、高压涡轮、低压涡轮)的流量和效率修正系数构成向量F，发动机气动热力学模型可进一步表示为：

(5)

z(t)=g(x(t),u(t),F)

(6)

由于实际的飞行数据已包含飞机进气道等对发动机的影响，因此利用飞行数据逆向求解式(6)所得的部件修正系数向量F是综合考虑飞机进气道、发动机性能衰退等因素对部件特性影响的综合修正系数。

F=G-1(x(t),u(t),z(t))

(7)

式(7)的求解须要满足测量参数的数量p大于等于部件修正系数数量n。本文研究对象虽然为电调控制，但仅有5个气路传感器(燃油流量Wf、高压转子转速NH、低压转子转速NL、高压压气机后总压Pt3、高压涡轮后总温Tt5)，因此式(7)的方程组求解为欠定问题，理论上无法求解。

针对上述欠定问题，Stamatis等[10]提出离散工作点分析(discrete operating points gas path analysis, DOPGPA)方法解决发动机健康因子求解过程中测量参数不足的问题，该方法假设发动机在单个工作循环中部件性能衰退程度相同，采用多个工作点拓展逆向求解方程组，从而为求解上述欠定问题提供了一种有效思路。后来该方法逐步发展为多工作点分析(multiple operating points analysis, MOPA)[10，13]方法，进一步证明了从有限测量参数中获取所有部件特性性能衰退的可能性。MOPA方法的目的是计算发动机健康因子，使发动机模型能够真实反映其工作状态，本质是对模型的修正。因此本文以MOPA方法为基础，利用多个稳态点修正发动机模型，解决基于飞行数据的发动机性能模型修正中存在的传感器数量不足的问题。

MOPA方法基于发动机单个工作循环中部件性能衰退程度相同的基本假设，而Diakunchak等[14]指出发动机不同工作状态下部件的流量和效率的衰退程度会随发动机工作状态的改变而变化，这就要求MOPA方法所选取的多工作点工作状态差异尽可能小，以近似满足MOPA方法部件性能衰退程度相同的假设。但Henriksson等[15]提出在多工作点的选取中，为减小测量噪声对方程组求解的误差，获得更好的方程适定性，选择的多个工作点之间工作状态应具有一定差异。因此MOPA方法在多工作点的选择上存在一定的矛盾。

为解决上述矛盾，本文在多工作点选择的问题上进行了折中，将发动机高压转子慢车以上转速分为4个区域(慢车～80%、80%～88%、88%～94%、94%～100%)，假设在每一区域内发动机满足MOPA基本假设(各部件修正系数不变)，且划分的区域范围足够大能够满足MOPA计算修正系数收敛的要求。

在单个区域范围内采用MOPA方法，对式(7)进行拓展：

(8)

式中：q为MOPA选择的工作点数量，且满足p×q≥n。

因此可将发动机修正系数方程组求解问题转化为优化问题，采用差分进化算法对优化问题进行求解。定义该优化问题的目标函数OF为：

(9)

差分进化算法是一种基于群体智能理论的优化算法[16]，通过种群内个体的合作与竞争实现全局范围内的搜索优化。该算法具有简单通用、全局搜索能力强等优点，在航空发动机性能仿真领域获得了广泛应用[17-18]。但由于修正系数计算须要花费大量时间，无法通过统计的方法选择最佳的控制参数S(缩放因子)、CR(交换率)。因此本文采用了一种称之为JADE的自适应差分进化算法[11]。

该方法选择自适应的方法调整控制参数，将产生更好个体的控制参数保留到下一代的计算中。通过自适应调整控制参数，提高算法的可靠性。同时该算法在贪婪策略DE/current-to-best的基础上引入了一种新的变异策略DE/current-to-pbest，该策略不仅利用了最优解的信息，还利用了其他优解的信息，且可以将存档的劣解与当前种群的差异纳入突变操作，使种群具有多样性，能够缓解早熟收敛等问题。与标准进化算法相比该方法在保证鲁棒性的同时，减少了进化代数。

具体的修正系数计算流程如图2所示。

图2 修正系数计算流程图

表1 区域1(慢车～80%)多工作点选取及修正误差

表2 区域2(80%～88%)多工作点选取及修正误差

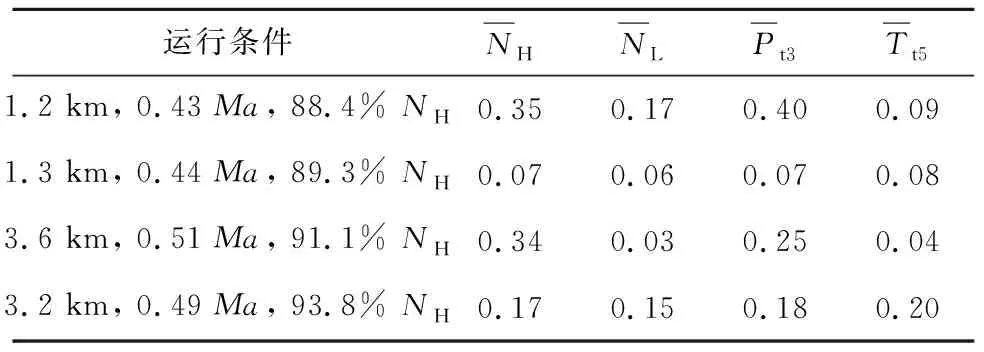
表3 区域3(88%～94%)多工作点选取及修正误差

表4 区域4(94%～100%)多工作点选取及修正误差

1.3 过渡态模型的建立

发动机的过渡态是指从一个稳定的工作状态到另一个稳定的工作状态的变化过程[5]。过渡态计算与稳态计算的差异主要体现在以下三方面：①过渡态工作过程中供油量发生变化，发动机功率平衡不再成立，转子转动惯量产生转子惯性；②过渡态工作过程中部件容腔内气体质量和能量发生变化，产生容积惯性；③过渡态工作过程中存在气体与固体的热交换，产生热惯性。因此为提高过渡态模型计算精度，使过渡态模型能真实反映实际发动机的工作过程，本文建模中综合考虑转子惯性、容积惯性和热惯性的影响。

1.3.1 转子惯性

在发动机过渡态工作过程中，由于供油量的变化导致剩余功率的产生，稳态计算中的转子扭矩平衡不再成立，考虑到过渡态过程中转子转速的加减速，需要在涡轮和压气机的扭矩平衡方程中加入转速的微分项进行修正：

(10)

(11)

式中：NH、NL分别为高、低压转子的转速；JH、JL分别为高、低压转子轴的转动惯量；MTH、MTL分别为高、低压涡轮输出的扭矩；MCH、MCL分别为高、低压压气机消耗的扭矩。

1.3.2 容积惯性

容积惯性与气体的可压缩性有关，在发动机工作状态发生剧烈变化时，容腔进出口气体流量、压力、温度发生一段时间的振荡，进出口气流参数不再相等。为充分考虑容积惯性对过渡态模型的影响，在该型发动机体积较大区域(风扇和压气机之间、燃烧室、高压涡轮和低压涡轮之间、外涵道)添加PROOSIS专用的容积惯性组件，该组件模拟一维气体动力学的质量、动量、能量，则简化的微分方程为：

(12)

(13)

(14)

式中：ρ为气体密度；V为容腔体积；Pg为气体的压力；Avol为容腔的横截面积；Wg为气体的流量；v为气体的流速；L为容腔的长度；H为气体的焓。

1.3.3 热惯性

在稳态计算中，通常假设气体与发动机部件之间处于热平衡，不存在热传递。然而，实际发动机运行过程中这种平衡是不存在的，因此为提高建模准确性，必须考虑发动机部件与气体之间的热传递问题。本文研究的对象为小涵道比涡扇发动机，为简化模型，在计算中仅考虑热端部件(燃烧室、高压涡轮、低压涡轮)的热传递。由于发动机各部件结构极为复杂，在计算过程中将发动机部件简化为温度分布均匀的板和恒定厚度的锥体。

燃气与理想部件间的传热平衡公式为：

(15)

式中：Cp为发动机理想部件的比热；m为发动机理想部件的质量；T(t)为发动机理想部件的温度随时间的函数；h为燃气和发动机部件之间的传热系数；At为发动机部件与燃气的传热面积。

(16)

ΔT(t)=ΔT0e-t/τ

(17)

式中：ΔT0为t=0时刻发动机部件和气体之间的温差，由式(17)可以看出部件的温度T一阶滞后于气体温度Tgas，滞后由时间常数τ决定。

2 结果与讨论

2.1 稳态模型的验证

为验证稳态模型计算的精度，随机选取其他飞行过程的稳定飞行数据进行对比，计算各飞行条件下发动机测量参数(NH、NL、Pt3、Tt5)的相对误差，如表5所示。

通过分析表5可以发现各个工作点的计算误差均在1.70%以内，其中Pt3、Tt5的计算误差相对较大。这与发动机压力、温度传感器误差较大有关，可见该模型能够满足稳态点计算工程精度要求。

表5 稳态点相对计算误差

2.2 过渡态模型仿真验证

提取发动机加速、减速段数据，对修正的发动机过渡态模型进行验证。在过渡态模型中输入进口压力P0、温度T0、飞行马赫数Ma，并将实时燃油流量作为过渡态的控制参数。

在进行过渡态计算时，计算了考虑综合瞬态效应(转子惯性、容积惯性和热惯性)和未考虑瞬态效应的模型，并将二者与真实发动机飞行参数进行了对比，见图3和图4。

图3 加速过程对比图

通过图3和图4的结果可以看出，发动机加减速过程中，模型的计算结果与飞行实际测量结果基本一致，综合考虑发动机瞬态效应的模型较仅考虑转子惯性的模型的计算结果与发动机实际数据更加贴合，考虑发动机综合瞬态效应的过渡态模型的计算误差在5.5%以内，仅考虑转子惯性的模型的计算误差在8.53%以内，因此，为使建立的模型能够满足工程精度要求，在过渡态建模过程中应综合考虑转子惯性、容积惯性和热惯性的影响。