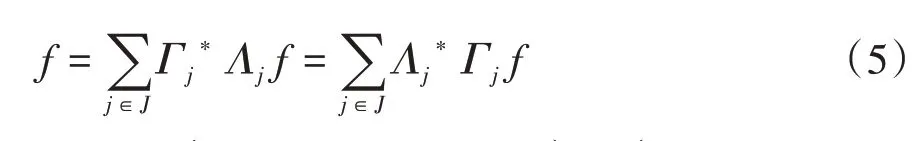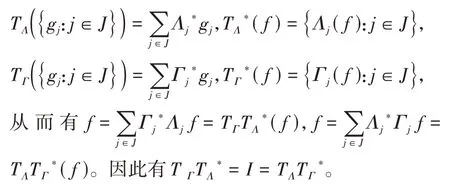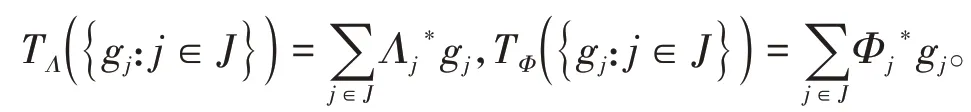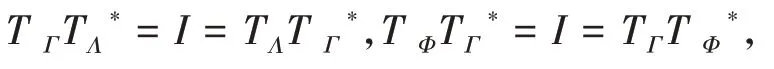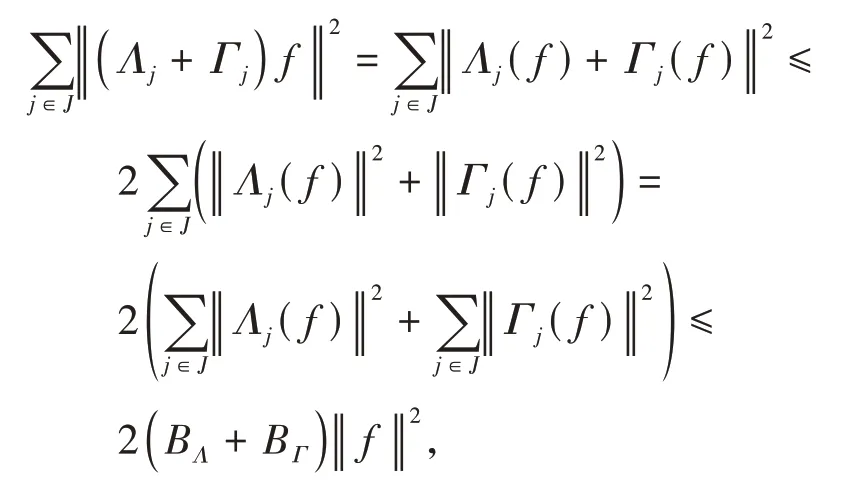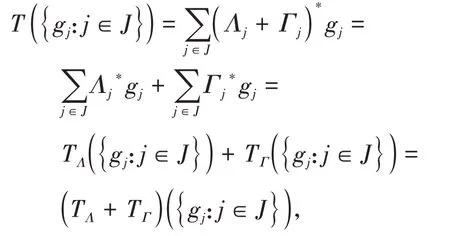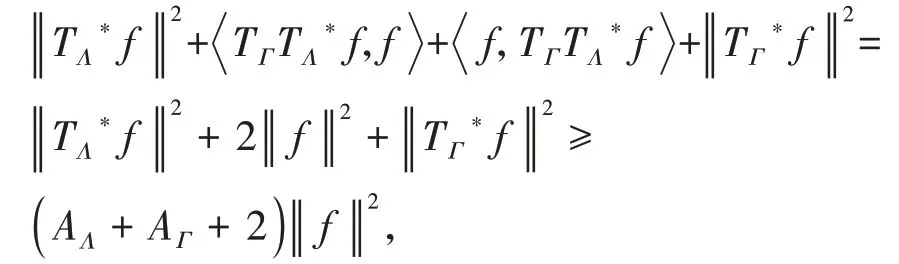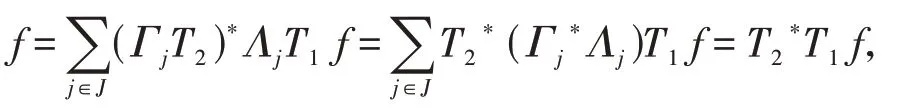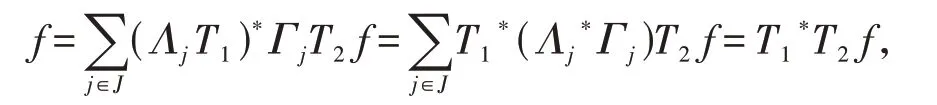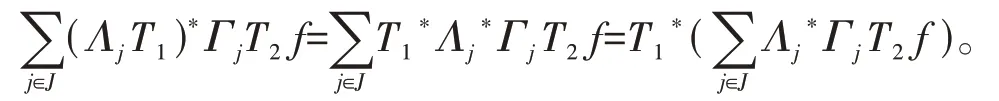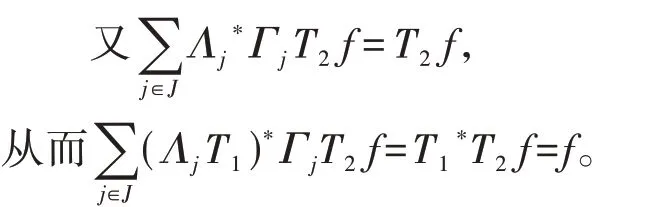关于g-框架与交错对偶g-框架稳定性的研究
2023-01-13张艳张建平
张艳,张建平
(延安大学数学与计算机科学学院,陕西 延安 716000)
框架理论是小波分析的主要研究内容之一。框架具有类似于基的性质,它比基有更好的灵活性。Hilbert空间H中的框架{ϕj}可以将H中的任意元素表示成的形式,但其系数cj一般不是唯一的。框架概念首先由DUFFIN等[1]在1952年为解决非调和Fourier级数的深层次问题而提出的,直到1986年,DAUBECHIES等[2]取得突破性研究。框架理论被应用到许多领域,如滤波器理论[3]、信号处理[4]、量子计算[5]等,从而开创了框架理论研究的新时代。之后,国内外许多学者对框架进行了深入研究,得到了大量有价值的研究成果[6-7]。2006年,SUN通过研究斜框架[8]、伪框架[9]、子空间框架[10]等概念,从中提炼出了g-框架的概念[11],并对g-Bessel序列、g-框架、g-Riesz基等相关概念及g-框架稳定性进行了研究[12]。算子是研究g-框架理论的一个重要工具,ZHU引入预框架算子的定义,使g-框架理论更加完善[13]。
文献[14]研究了Hilbert空间中g-框架在Sα(α∈R)作用下的稳定性及在可逆算子作用下的稳定性。本文第二部分在此基础上进行推广,研究g-框架在余等距算子、有界算子、满射算子作用下的稳定性,给出了g-Bessel序列成为g-框架的条件以及两个g-框架的直和仍为g-框架的条件。文献[15]通过有界算子与g-框架相结合,给出g-框架对在算子扰动下为g-框架的几个结果。受其启发,本文第三部分给出交错对偶g-框架的定义,研究两个g-Bessel序列成为交错对偶g-框架的充要条件,证明了互为交错对偶的两个g-框架的和是g-框架,并给出互为交错对偶的两个g-框架分别在可逆算子作用下仍互为交错对偶g-框架的充要条件。
1 预备知识
本文用U和V表示两个Hilbert空间,{Vj:j∈J}是V中的一列闭子空间,J是可数的指标集,用L(U,Vj)表示所有从U到Vj的有界线性算子的集合。若Vj=U,记L(U,Vj)=L(U),此时称IU为U上的恒等算子,
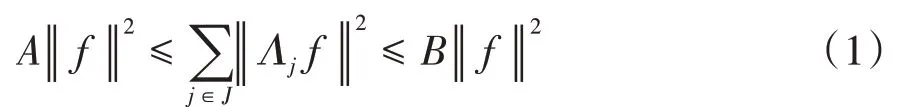
定义1[14]设{Λj∈L(U,Vj):j∈J}是Hilbert空间U中的一个算子列,如果存在两个正常数0 定义2[16]设{Λj∈L(U,Vj):j∈J}是U关于{Vj:j∈J}的g-框架当且仅当TΛ:l2({Vj:j∈J})→U,是可定义的有界线性算子,就称TΛ为{Λj∈L(U,Vj):j∈J}的前框架算子。它的共轭算子TΛ*:U→l2({Vj:j∈J}),TΛ*f={Λj(f):j∈J}称作是{Λj∈L(U,Vj):j∈J}的分析算子。对于g-框 架{Λj∈L(U,Vj):j∈J}称有界算子SΛ:Λj f为{Λj∈L(U,Vj):j∈J}的框架算子,SΛ是一个线性、有界、自伴、正的可逆算子[17]。 定义3[18]设H是Hilbert空间,Q是H上的线性有界算子,如果对∀f∈H,‖Q*f‖=f,那么算子Q称为余等距算子(其中Q*为算子Q的共轭算子)。 引 理1[16]设{Λj∈L(U,Vj):j∈J}是U关 于{Vj:j∈J}的g-框架,令T:U→U是U的可逆算子,则{ΛjT∈L(U,Vj):j∈J}是U关于{Vj:j∈J}的g-框架。 引理2[19]设T:U→K为有界满算子,存在有界算子T+:K→U,使得TT+:K→K,TT+f=f,则称T+为T的伪逆。 引理1说明g-框架{Λj∈L(U,Vj):j∈J}在可逆算子作用下仍为g-框架,下面定理1表明它在余等距算子的作用下仍然是g-框架。 定理1设{Λj∈L(U,Vj):j∈J}是U关于{Vj:j∈J}的g-框架,且它的下、上框架界分别为A、B,Q:U→U是余等距算子,若Γj=ΛjQ,则{Γj∈L(U,Vj):j∈J}是U关于{Vj:j∈J}的g-框架,且框架界分别为A、B。 证明由g-框架的定义知,对∀f∈U有 成立,由此可以得到 又因为 根据余等距算子的定义有‖Q*f‖=f,所以 接下来讨论g-框架{Λj∈L(U,Vj):j∈J}在有界算子的作用下仍为g-框架的充分必要条件。 定理2设{Λj∈L(U,Vj):j∈J}是U关于{Vj:j∈J}的g-框 架,S:U→U是有界算子,则{ΛjS∈L(U,Vj):j∈J}是g-框架的充分必要条件为,其中α为正常数。 证明必要性:设{Λj∈L(U,Vj):j∈J}是U关于{Vj:j∈J}的g-框架,其下、上框架界分别为A、B,则对于∀f∈U,有 若g-框架{ΛjS∈L(U,Vj):j∈J}的框架界为M、N,根据g-框架的定义知对∀f∈U,有 成立,同时可得 因此结合式(2)和式(3)得 故对∀f∈U,取结论成立。 充分性:假设存在α>0,对∀f∈U,满 足,则有 所以{ΛjS∈L(U,Vj):j∈J}是U关于{Vj:j∈J}的g-框架且其框架界为Aα和B‖S‖2。 推论1设{Λj∈L(U,Vj):j∈J}是U关于{Vj:j∈J}的g-框架且它的下、上框架界为A和B,若S∈L(U),则{ΛjS∈L(U,Vj):j∈J}是U关 于{Vj:j∈J}的g-框架当且仅当S是有界满射算子,此时{ΛjS∈L(U,Vj):j∈J}的框架界为和。 证明若S是有界满射算子,由引理2得知,存在伪逆算子S+使得SS+=IU,故对∀f∈U,有,取,由定理2知结论成立。 定理3设{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}是U关于{Vj:j∈J}的两个g-框架,TΛ、TΓ分别为其前框架算子,设S1、S2∈L(U),若TΛTΓ*=0且S1或S2是满射算子,则{ΛjS1+ΓjS2∈L()U,Vj:j∈J}是U关于{Vj:j∈J}的g-框架。 证明因为{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}是U关于{Vj:j∈J}的两个g-框架,故存在正常数0 成立,又因为TΛTΓ*=0,根据前框架算子的定义,对∀f∈U,有 不失一般性,假设S1是满射算子,由推论1证明过程可知存在常数α,使得对∀f∈U,有,由此可得 所 以{ΛjS1+ΓjS2∈L(U,Vj):j∈J}是U关 于{Vj:j∈J}的g-框架。 推论2设{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}是U关于{Vj:j∈J}的两个Parserval g-框架,且TΛTΓ *=0,则{Λj+Γj∈L(U,Vj):j∈J}是U关 于{Vj:j∈J}的框架界为2的Parserval g-框架。 定理4设{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}是U关于{Vj:j∈J}的g-Bessel序列,且满足f=Λj f,∀f∈U,则{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}都是U关于{Vj:j∈J}的g-框架。 证明设正数B、D分别为{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}的Bessel界,则对∀f∈U, 设U和X都是Hilbert空间,若,则我们称U⊕X为两个Hilbert空间的直和,此时U⊕X也是Hilbert空间。且定义内积为 设U和X都 是Hilbert空 间,Λj∈L(U,Vj),Γj∈L(X,Wj),∀f∈U,∀g∈X, 定理5设{Λj∈L(U,Vj):j∈J}是U关于{Vj:j∈J}的g-框架,其下、上框架界分别为A和B,{Γj∈L(X,Wj):j∈J}是X关 于{Wj:j∈J}的g-框架,其下、上框架界分别为C和D,则{Λj⊕Γj∈L(U⊕X,Vj⊕Wj):j∈J}是g-框架且其框架界为min{A,C}和max{B,D}。当SΛ、SΓ、SΛ⊕Γ分别是Λ、Γ、Λ⊕Γ的框架算子,则SΛ⊕Γ=SΛ⊕SΓ。 证明对∀f∈U,∀g∈X,由式(4)得 由于对∀f∈U,∀g∈X, 定义4设{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}是g-Bessel序列,当满足对∀f∈U,有 成立,则称{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}是交错对偶g-框架。 由交错对偶g-框架的定义,给出g-Bessel序列为交错对偶g-框架的充要条件。 定理6设{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}是g-Bessel序列,TΛ、TΓ分别为其前框架算子,则{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}为交错对偶g-框架当且仅当TΓTΛ*=I=TΛTΓ*。 证明必要性:设{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}为交错对偶g-框架,根据交错对 偶g-框架的定义,可知对∀f∈U,有f=成立。 根据g-框架的前框架算子和分析算子的定义,可以得到 充分性:设TΓTΛ*=I=TΛTΓ*,因为=f,所 以 根 据交错对偶g-框架的定义,{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}为交错对偶g-框架。 定理7设TΓ是{Γj∈L(U,Vj):j∈J}的前框架 算 子,{Λj∈L(U,Vj):j∈J}和{Φj∈L(U,Vj):j∈J}都是{Γj∈L(U,Vj):j∈J}的交错对偶g-框架,若TΓ*TΓ=I,则 {Λj∈L(U,Vj):j∈J}和{Φj∈L(U,Vj):j∈J}为交错对偶g-框架。 证明设TΛ、TΦ分别是{Λj∈L(U,Vj):j∈J}和{Φj∈L(U,Vj):j∈J}的前框架算子,则 根据定理6知 又因为TΓ*TΓ=I,所以有 即TΦTΛ*=I=TΛTΦ*。 从而,由定理6可得{Λj∈L(U,Vj):j∈J}和{Φj∈L(U,Vj):j∈J}为交错对偶g-框架。 定理8设{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}是交错对偶g-框架,则{Λj+Γj∈L(U,Vj):j∈J}是U关于{Vj:j∈J}的g-框架。 证明一方面,设AΛ、BΛ为{Λj∈L(U,Vj):j∈J}的g-框架界,AΓ、BΓ为{Γj∈L(U,Vj):j∈J}的g-框架界,TΛ、TΓ分别为其前框架算子,因为{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}是交错对偶g-框架,由定理6得TΓTΛ*=I,所以对∀f∈U, 即证得{Λj+Γj∈L(U,Vj):j∈J}是g-Bessel序列。 另一方面,设{Λj+Γj∈L(U,Vj):j∈J}的前框架算子为T,则 从而有T=TΛ+TΓ,又因为{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}是交错对偶g-框架,根据定理6知TΓTΛ*=I=TΛTΓ*,故对∀f∈U, 显然AΛ+AΓ+2>0,所以{Λj+Γj∈L(U,Vj):j∈J}是U关于{Vj:j∈J}的g-框架。 推论3设{ΛjT1∈L(U,VJ):j∈J}和{ΓjT2∈L(U,VJ):j∈J}为交错对偶g-框架,其中T1、T2∈L(U)都为可逆算子,则{ΛjT1+ΓjT2∈L(U,VJ):j∈J}是U关于{Vj:j∈J}的g-框架。 定理9设{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}是交错对偶g-框架,T1、T2∈L(U)都为可逆算子,则{ΛjT1∈L(U,VJ):j∈J}和{ΓjT2∈L(U,VJ):j∈J}为交错对偶g-框架当且仅当T1*T2=I=T2*T1。 证明根据引理1可知,{ΛjT1∈L(U,VJ):j∈J}和{ΓjT2∈L(U,VJ):j∈J}都为g-框架。 必要性:设{ΛjT1∈L(U,VJ):j∈J}和{ΓjT2∈L(U,VJ):j∈J}为交错对偶g-框架,因为{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}是交 错对偶g-框架,根据定理6可知对∀f∈U, 即得T2*T1=I; 充分性:设T1*T2=I=T2*T1,则 因为{Λj∈L(U,Vj):j∈J}和{Γj∈L(U,Vj):j∈J}是交错对偶g-框架,所以,从而 同理,对∀f∈U, 根据交错对偶g-框架的定义,可知所证结论成立。2 g-框架的稳定性
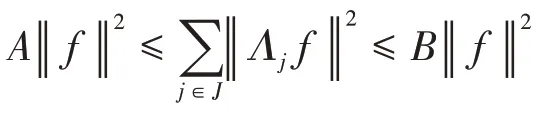

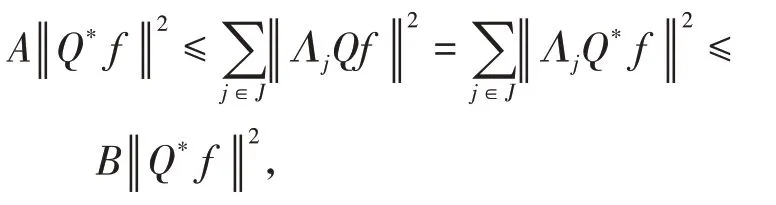
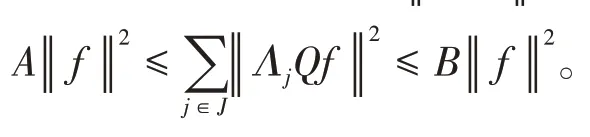

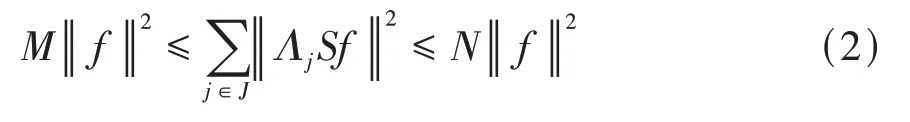

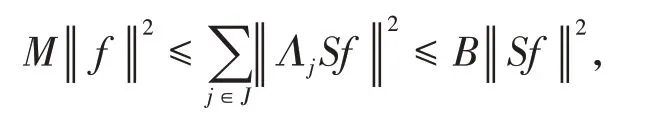
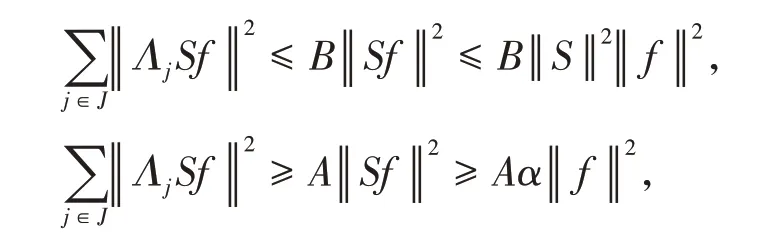
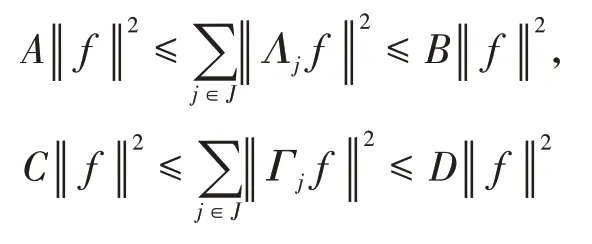

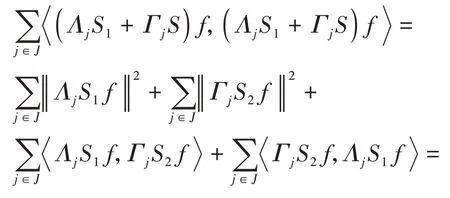


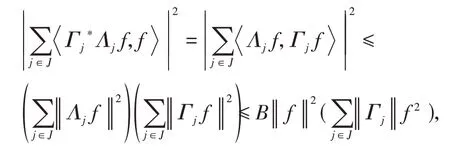
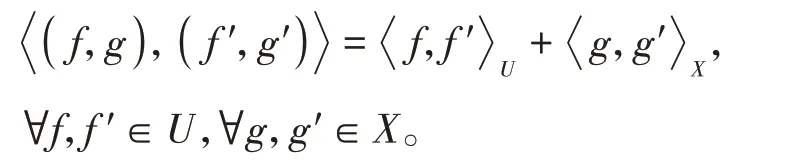
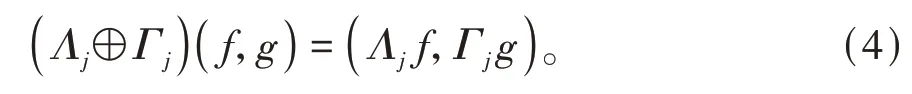
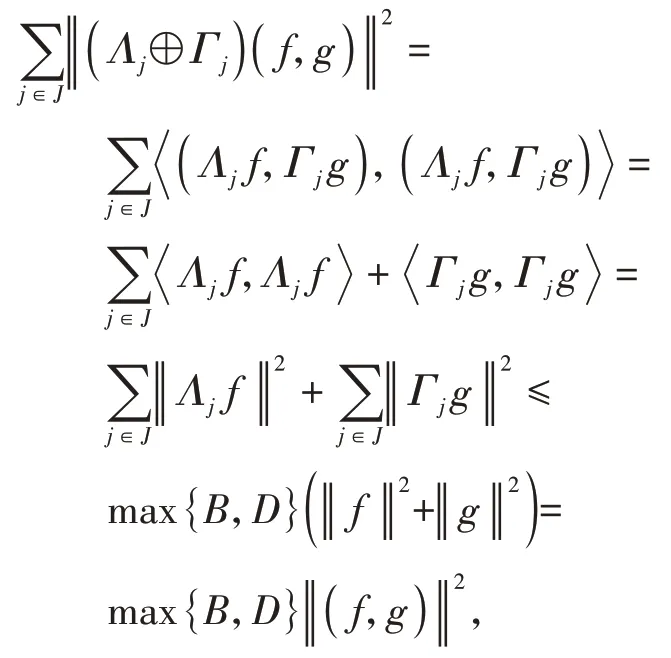
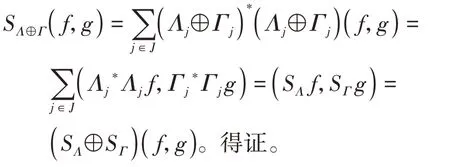
3 交错对偶g-框架的稳定性