人工冻结斜井冻结壁开挖后孔口应力分析
2023-01-13孙杰龙任建喜
孙杰龙,任建喜
(1.延安大学建筑工程学院,陕西 延安 716000;2.西安科技大学建筑与土木工程学院,陕西 西安 710054)
在地层含水量大、煤层埋深较浅、土质松软的地区常采用竖向直排人工冻结斜井对井筒进行开凿[1]。冻结壁作为一种临时的承载结构,其作用主要是在井筒开凿初期为施工提供安全保障,若冻结壁强度不够或变形过大,则极易发生涌水、溃砂事故,对人员生命安全造成威胁,同时也会带来巨大的经济损失[2-8]。
目前,由于斜井冻结法设计理论缺乏科学依据,难以满足工程需求,因此在进行竖向直排人工冻结斜井凿井时,往往要借鉴立井冻结法凿井经验[9-14]。现在对立井冻结壁的研究成果已经很多,但对于斜井冻结壁的研究成果还相对较少,尤其对开挖后斜井冻结壁孔口的应力分析更是少见。基于此,本文将对竖向直排人工冻结斜井冻结壁开挖后孔口应力进行分析,研究结果可为斜井冻结法凿井设计提供一定的理论基础。
1 冻结壁开挖孔口受力分析
竖向直排人工冻结斜井冻结壁开挖后,孔边的应力将远大于无孔时的应力,也远大于距孔稍远处的应力,这种现象称为孔边应力集中。而孔边应力集中与想象中因截面减少而应力有所增大相差很大,即有孔时截面面积即使只减小了百分之几甚至千分之几,应力集中也会达到几倍以上,且对于形状一样的孔来说,应力集中的倍数与孔的大小关系不大。实际上是由于孔的存在,孔附近的应力、应变状态会完全改变。
不同于立井冻结,斜井冻结所形成的冻结壁其形状可视作矩形,如图1所示。
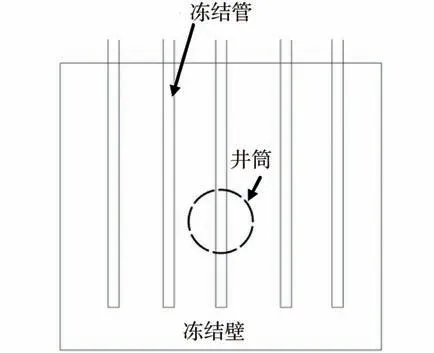
图1 斜井冻结壁
为了分析斜井冻结壁开挖后孔口的应力状态,取厚度为d的冻结壁为研究对象,当d远小于冻结壁长度和宽度时,所选取的冻结壁可视为薄板。假设开挖后冻结壁孔口为圆形,其半径为a,这样开挖后斜井冻结壁孔口应力分析,就可简化为矩形薄板在距离边界较远处有半径为a的小圆孔。以小圆孔圆心为坐标原点,以远大于a的某一长度b为半径,作一个大圆,在四边受均布压力,集度分别为q1和q2,其中q2=λq1,λ为侧压力系数。由于是小孔口问题,则要保证以b为半径的大圆全部落在弹性体内,在此需假设开挖那一瞬间冻结壁处于弹性状态,且未冻土也处于弹性状态,不考虑冻结壁与未冻土间的相互作用,如图2所示。
为了简化计算,可将荷载图2分为两部分:第一部分,是四边的均布拉力,如图3A所示,记为工况Ⅰ;第二部分为左右两边受均布拉力和上下两边受均布压力,如图3B所示,记为工况Ⅱ。其中:q=。
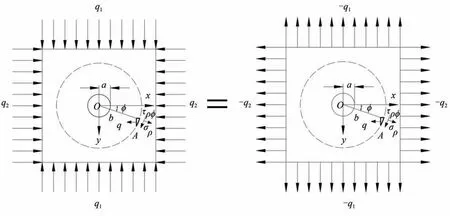
图2 冻结壁受力简图
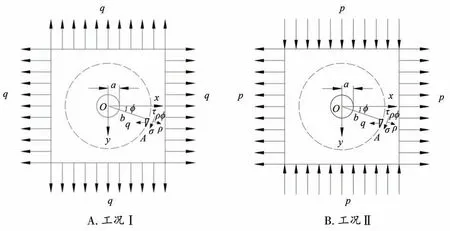
图3 荷载分解图
2 工况Ⅰ冻结壁孔口应力分析
如图3A所示,根据圣维南原理,大圆圆周某点A处的应力与开挖 前 相同,即:σx=q,σy=q,τxy=0,其中σx为x向正应力,σy为y向正应力,τxy为剪应力。由于直边的边界条件采用的是直角坐标系,而本文主要分析冻结壁开挖后圆孔周边应力,所以首先要将直角坐标变为极坐标,式(1)为直角坐标系向极坐标的变换式。
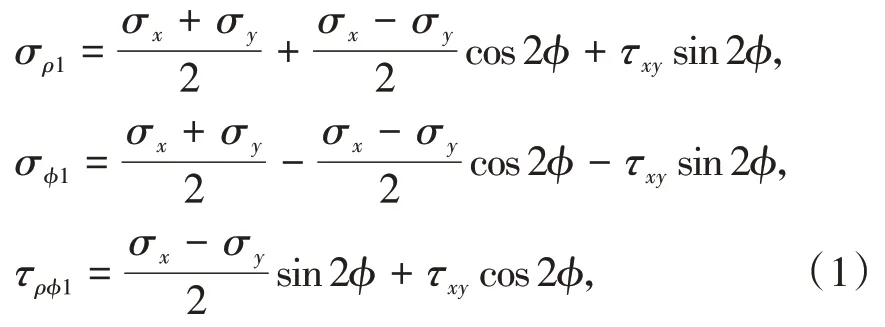
其中,σρ1为径向正应力,τϕ1为环向正应力,τρϕ1为剪切应力。将σx=q,σy=q,τxy=0代入到式(1)中,可得A点的极坐标应力分量σρ1=q,τρϕ1=0,则上述问题可转化为以a为内半径,以b为外半径的圆环,某点M在外边界上受均布拉力q问题,则其极坐标应力分量可表示为

其中,ρ为M点到坐标原点的距离。
由于b远大于a则式(2)可简化为
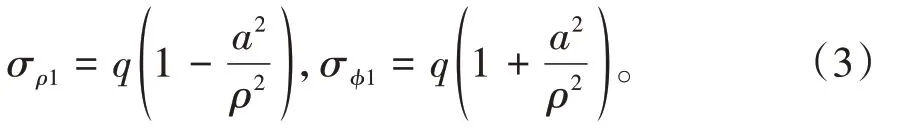
由式(3)可知,当ρ=a时,σρ1=0,σϕ1=2q,由此可知,受均布拉应力时,冻结壁开挖后沿孔边的应力为开挖前的2倍。
3 工况Ⅱ冻结壁孔口应力分析
如图3B所示,在矩形薄板的两边受有均布拉力p,而在上下两边受有均布压力p,则σx=p,σy=-p,τxy=0,将其代入到式(2)可得在极坐标系下,ρ=b和ρ=a处的边界条件分别为
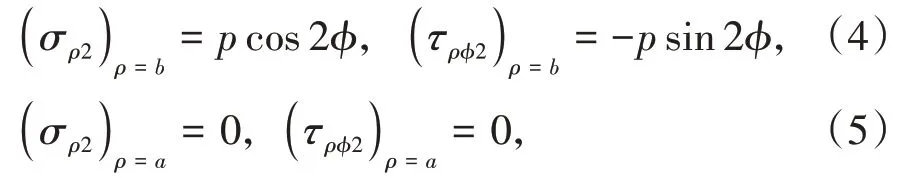
其中,σρ2为径向正应力,τρϕ2为剪应力。采用半逆解法对式(4)进行求解,假设σρ2、τρϕ2分别为ρ的函数乘以cos 2ϕ和sin 2ϕ,则有

因此,可作如下假设:

将式(7)代入极坐标中的相容方程可得
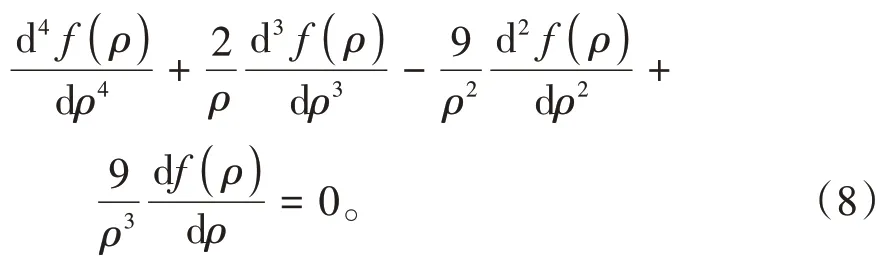
对式(8)进行求解,可得
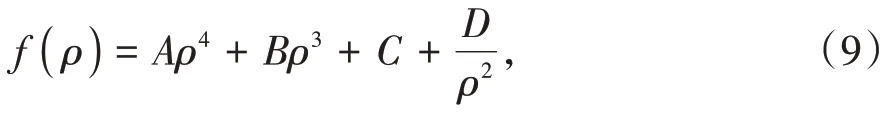
其中,A、B、C、D为任意常数,将式(9)代入式(7)可得极坐标下的应力函数为
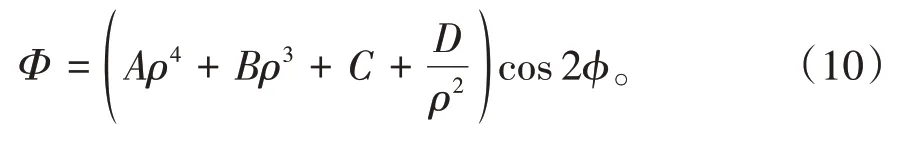
则应力分量的表达式为
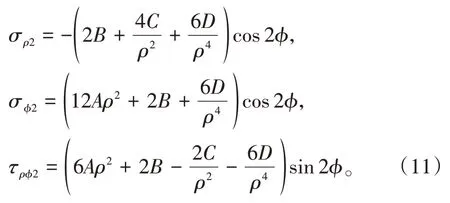
将式(11)分别代入式(4)和式(5)可得
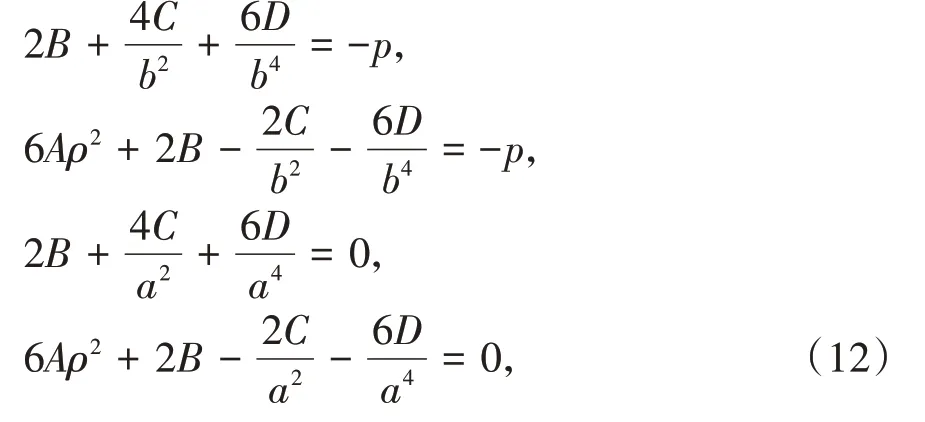
解式(12)求解A、B、C、D可得
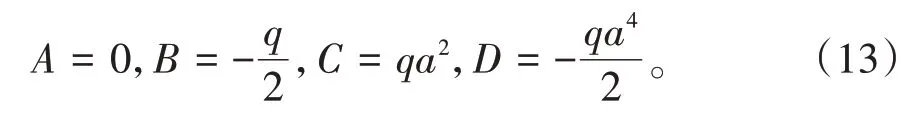
将式(13)代入式(11)可得应力分量的表达式为

由 式(14)可 知,当ρ=a时,σρ2=0,σϕ2=-4pcos 2ϕ,其最大值为4p,最大位置为ϕ=的孔边;最小值为-4p,最小位置为ϕ=0或π的孔边,两者均为无孔(开挖前)时的4倍。
将式(3)和式(14)叠加可得原荷载作用下冻结壁开挖后的应力分量为
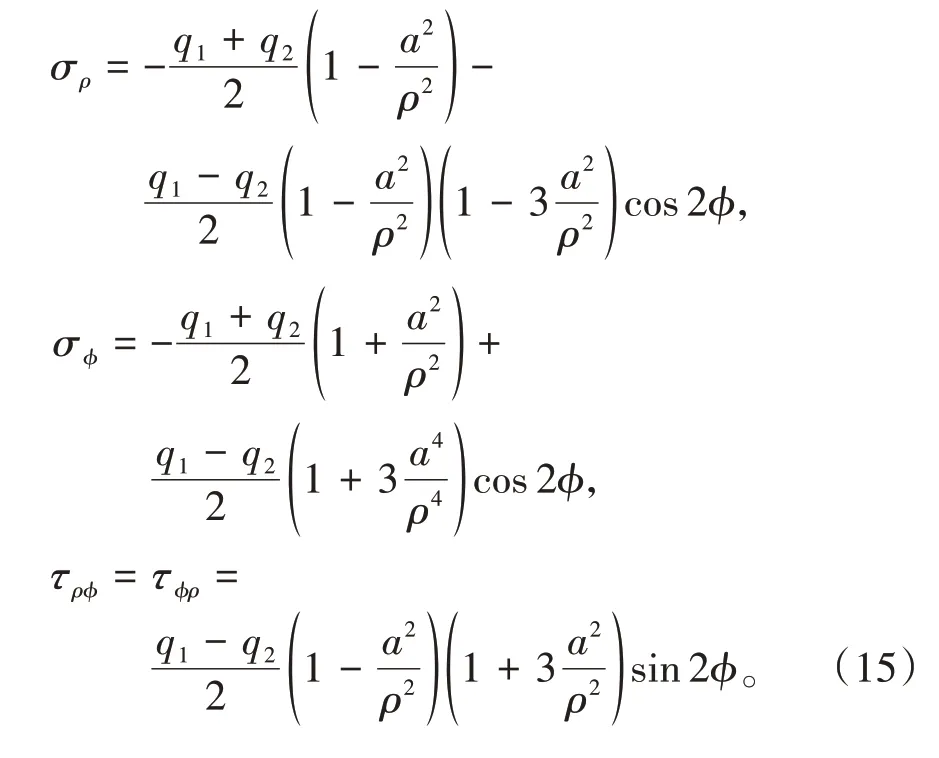
将q2=λq1代入式(15)可得
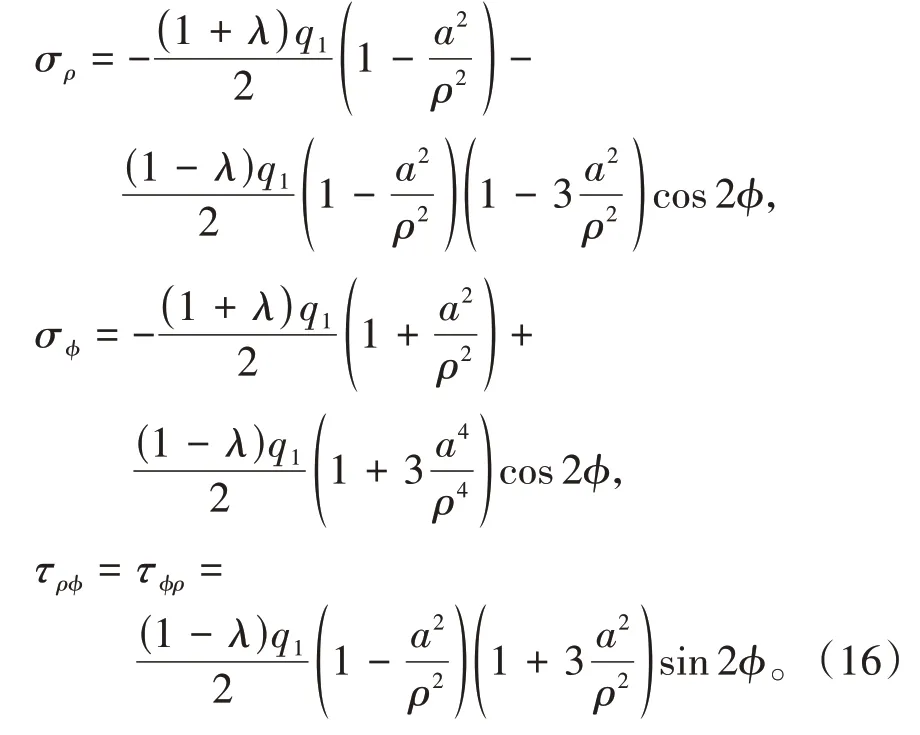
由式(16)可知,当ϕ=90°时,式(16)可简化为
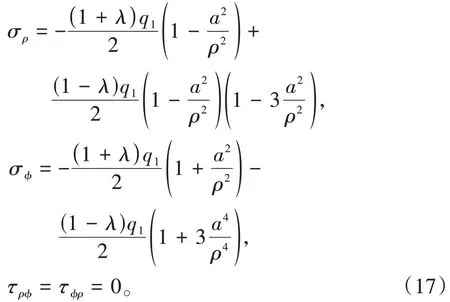
当ϕ=0或180°时,式(16)可简化为
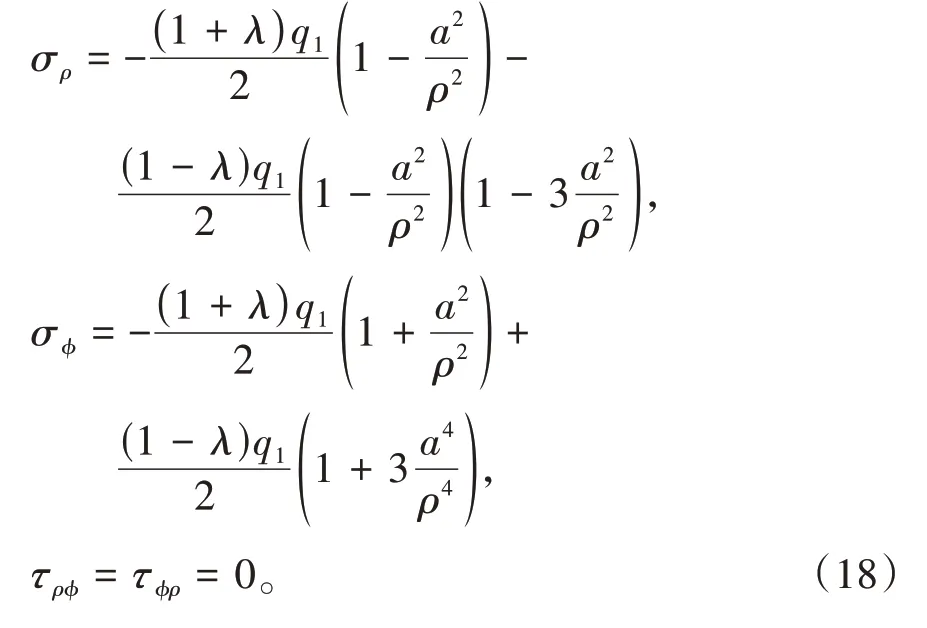
4 算例分析
袁大滩煤矿主斜井采用冻结法施工,斜井井筒长1 303.3 m,倾角14°,冻结段总斜长377 m,水平长度365.8 m,井筒开孔半径2.5 m。井筒冻结垂深20~111.208 m。斜井井筒采用多排管局部冻结方案凿井,每排5个冻结孔,排距2.35 m,考虑冻结影响范围所形成的冻结壁宽度为12 m。砂土物理力学参数试验结果如表1所示[15]:
取井筒埋深为100 m处为研究对象,侧压力系数取0.84,建立数值分析模型,如图4所示。数值计算时a取0.2 m,模型长×宽=12 m×12 m,在模型左右两条边界施加Y向约束,允许其在X向变形,在模型上下两条边界施加X向约束,允许其在Y向变形。
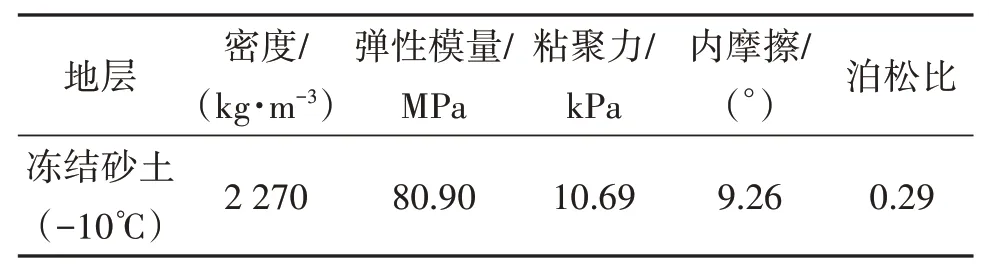
表1 砂土物理力学参数
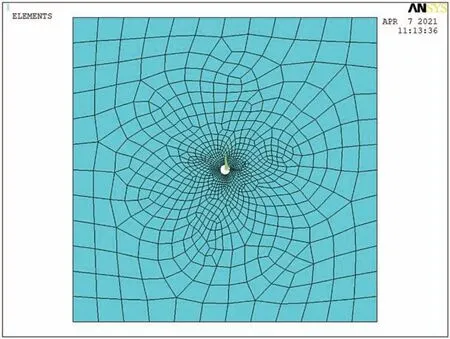
图4 计算模型
数值计算模型为轴对称模型,故取1/4模型进行分析,数值模拟计算结果和理论计算结果如图5所示。
图5A为竖向应力云图,沿Y轴的应力分布可近似视为ϕ=90°处的径向应力,沿X轴的应力分布可近似视为ϕ=0或180°处的环向应力。由图5A可知,随着ρ增大,ϕ=90°处的径向应力迅速减小,而ϕ=0或180∘处的环向应力增大,其最小值为初始压力的(1-3λ)倍;当ρ/a≈11时,径向应力和环向应力趋于稳定,其稳定值为侧压力1 906 800 Pa。
图5B为水平向应力云图,沿Y轴的应力分布可近似视为ϕ=90°处的环向应力,沿X轴的应力分布可近似视为ϕ=0或180°处的径向应力。由图5B可知,随着ρ增大,ϕ=90°处的环向应力迅速增大,其最小值为初始压力的(λ-3)倍;ϕ=0或180°处的径向应力随着ρ增大而减小,当ρ/a≈11时,环向应力和径向应力趋于稳定,其稳定值为初始压力2 270 000 Pa。
由数值模拟和理论计算结果对比可知,两者计算结果存在一定的误差,这是由于在数值模拟计算过程中网格划分、约束条件简化等因素引起的。但数值计算结果和理论计算结果基本一致,较好的反应了竖向直排人工冻结斜井冻结壁开挖时应力分布的基本规律。
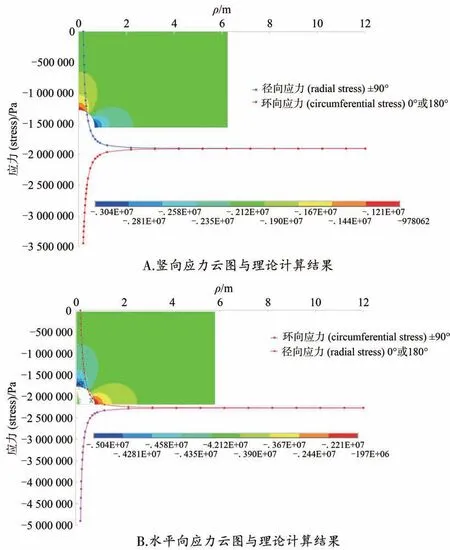
图5 理论计算与数值计算结果对比分析
5 结论
1)冻结壁开挖后其孔边环向应力分布与侧压力系数有关,在ϕ=90°处,冻结壁孔口处环向应力为未开挖前的(λ-3)倍,且应力沿径向逐渐增大到初始压力。
2)冻结壁开挖后在ϕ=0或180°处,冻结壁孔口处的环向应力为未开挖前的(1-3λ)倍,且应力沿径向逐渐增大到侧向压力。
3)冻结壁开挖后在ϕ=90°处孔边径向应力由0迅速减小,并在ρ/a≈11时减小到侧压力;在ϕ=0或180°处孔边径向应力由0迅速增大,并在ρ/a≈11时增大到初始压力。
