基于摩尔库伦准则的数值流形法岩体破坏模拟分析
2023-01-13高文伟
高文伟
(延安大学建筑工程学院,陕西 延安 716000)
随着工程建设难度不断增加,岩质边坡工程、地基工程、隧道工程中岩体破裂失稳都与岩石裂纹扩展密切相关[1-3]。岩石裂纹扩展过程本身是从连续体到不连续体转化的过程,岩石裂纹扩展过程研究对岩体裂纹模型与本构关系的建立、岩石体变形断裂机制的揭示以及岩体工程稳定性评价都具有重要意义[4]。
近几年,随着数值计算方法的不断发展和计算机能力的不断提高,数值分析方法在岩石裂纹扩展研究中得到越来越多的应用[5-6]。其中,数值流形法在处理岩石非连续性方面表现出了极大的优势,并逐渐得到了重视[7-8]。NING等[9]运用数值流形法对岩体裂纹扩展进行了研究,该方法通过建立数学覆盖和物理覆盖系统,实现了对连续问题和非连续问题的统一求解,使得岩体裂纹扩展不受网格划分的影响,在岩石裂纹问题上表现出了很好的优势和前景。MA等[10]结合断裂力学裂纹尖端的研究理论,根据裂纹尖端的应力强度因子,以最大周应力准则为判据,判断裂纹扩展问题,在岩石爆破、水力压裂等方面取得了一定的研究成果。张国新等[11-12]研究了二阶流形法,借鉴有限单元法的二阶位移函数的构造方法,用6节点三角形构成数学网格,用常数覆盖函数和二阶权函数构成二阶流形元法的位移函数,通过改进的程序得出了二阶流行法能够较高精度的分析解决一般结构的变形问题和接触问题。徐栋栋等[13]通过对裂纹尖端附近的网格加密即通过在裂纹尖端影响区域内的物理片上增加用于模拟应力奇异性的增强位移函数的方法,保证了裂纹扩展能够在细分的网格中进行,减小了裂纹扩展对网格的依赖,扩展了数值流形法。本文采用摩尔库伦破坏准则,对数值流形方法进行分析,然后建立数值分析模型,对岩体在裂纹扩展模式进行分析研究,为岩体破裂研究提供新的思路。
1 数值流形方法
1.1 覆盖位移原理及函数表达
数值流形方法是把有限覆盖系统连接在一起,用以覆盖全部材料体可用局部覆盖所定义的函数来计算的方法。数学网格和物理网格相互重叠形成物理覆盖。数学网格只定义数值解的精,它由用户选择;物理网格通常由材料的裂缝、边界和分区界面等材料的物理及几何性质所决定。两套覆盖系统在处理非连续性问题时只对物理覆盖进行更新,数学网格并不更新。
采用有限单元覆盖的数值流形方法,每个物理覆盖都具有独立的位移函数,因此在裂纹两侧由独立的位移函数描述。图1A表示含裂纹尖端的材料,流形单元被裂纹切割分为2种情况:完全切割(单元a),部分切割(单元b和单元c)。单元a是由3个数学覆盖表示Mi(i=1,2,3),3个数学覆盖形成6个独立的物理覆盖和(i=1,2,3),单元a被裂纹切割成2个独立的流形单元a1(裂纹以上部分)和单元a(2裂纹以下部分),a1由物理覆盖(i=1,2,3)描述,a2由物理覆盖(i=1,2,3)描述,裂纹的相对位移为式(1)计算得到。
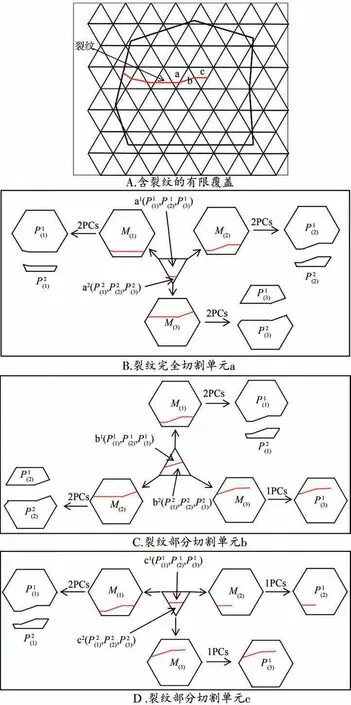
图1 含裂纹的NMM
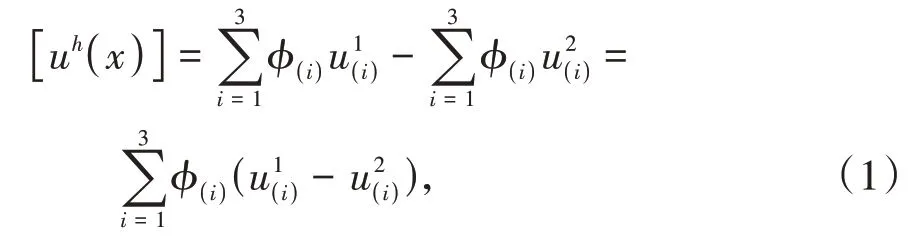
其中,ϕ(i)为各物理覆盖的势函数,为不同的多项式,因此裂纹两侧就会发生相对位移。单元c是由3个数学覆盖表示Mi(i=1,2,3),受到裂纹的影响,3个数学覆盖形成4个独立的物理覆盖与,单元c被裂纹切割成2个流形单元,单元c1(裂纹以上部分)和单元c2(裂纹以下部分),c1由物理覆盖(i=1,2,3)描述,c2由物理覆盖、描述,裂纹的相对位移为
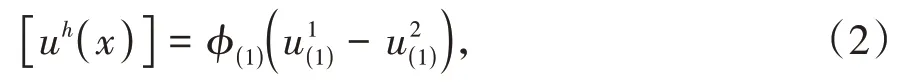
其中,ϕ(1)为各物理覆盖M1的势函数,为不同的多项式,因此裂纹两侧有部分相对位移,这也就是裂纹尖端的奇异性。
1.2 块体破裂算法
在数值流形开裂算法中,首先求解各流形单元的应力状态,由于流形单元面积太小,不能准确表示开裂区域即裂纹尖端周围的应力状态,因此以物理覆盖为基本单位进行开裂判断,求出各个物理覆盖应力状态,根据开裂准则判断是否发生开裂,若物理覆盖应力状态达到开裂条件,则覆盖中的单元发生开裂,根据覆盖中最大主应力和最大剪应力以及块体周边现有的裂纹尖端情况,确定其开裂性质以及开裂发生的方向和位置,规定开裂面在一个时步内贯穿一个流形单元,并考虑单元破裂过程中的能量损耗。
以摩尔库伦准则为判据判断裂纹扩展,记压应力为正。在每个物理覆盖上,最大主应力、最小主应力分别为σ1和σ3,根据摩尔应力圆理论,在与最小主应力σ3方向呈β角的面上的法相应力和剪应力分别为σ和τ,其中
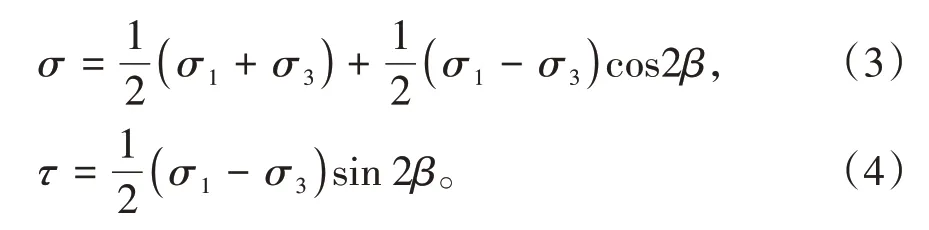
岩石强度曲线服从库伦准则:

其中,c,φ分别为岩石粘聚力和内摩擦角。
将式(3)、(4)代入式(5)可得
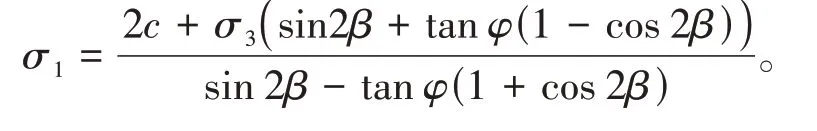
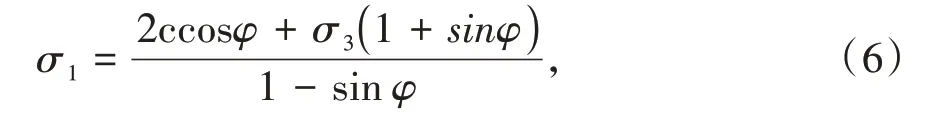
最小主应力满足-σ3=T0时,T0为岩石的抗拉强度,岩石发生剪切破坏。
2 岩体破裂模拟
将该方法应用于岩体模型破裂模拟以验证其适用性,建立试样如图2A所示,试样尺寸为5 cm×10 cm(宽×高),试样中心处设置1条与水平方向夹角为45°、长13 mm、宽0.5 mm的预设裂纹,对应建立的数值流形网格模型如图2B所示。为了验证模型的正确性,岩体模型结果与ZHANG[14]的试验结果进行对比,试样的参数见表1。试验采用位移控制伺服加载函数,当出现峰值应力后,轴向应变达到10%时,试验终止。
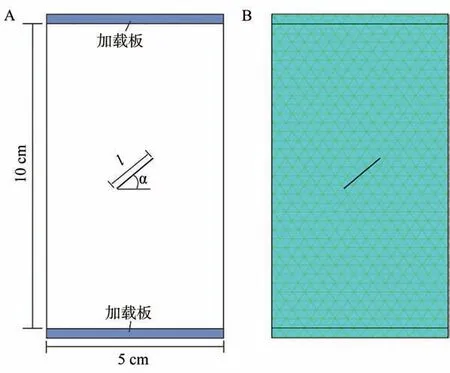
图2 岩体单轴压缩模型:(A)二维试样中包含的单个预设裂缝(α=45°,l=13 mm);(B)与物理试验相同高度和宽度的数值流形模型

表1 模拟试样的力学参数[10]
2.1 压缩条件下岩体破裂裂隙扩展
图3是含有预设裂纹的试样模拟结果,模型黑色表示裂纹扩展形态,图3A-E中分别显示的计算时步为10步、100步、200步、300步和400步,可以看出预设裂纹尖端首先产生微裂纹(图3B),表明裂纹尖端有应力集中,随着试样应变的增大,裂纹逐步向试样上下扩展(图3C-E),与ZHANG[14]的试验结果(图3F)比较可以看出,本次模拟的裂纹扩展模式和形态与岩体实际扩展一致,次生裂纹均在裂纹尖端进行启裂,并以曲线路径延伸扩展至试样顶部和底部,模拟结果说明本文所引入的摩尔库伦破坏准则对于模拟岩石破裂具有较好的效果。

图3 岩石开裂过程模拟结果:(A)-(E)数值模拟结果;(F)实验结果[10]
2.2 应力与裂纹尖端应变特性分析
为了更好的对比预设裂纹对岩体强度的影响,在裂隙岩体模拟过程中,记录加载板的应力和应变参数,并与完整岩体的应力应变结果进行对比,绘制试样的应力-轴向应变的关系曲线,如图4所示。可以看出,对于完整的岩体试样,存在明显的弹性阶段,该阶段的曲线平直,屈服阶段极短,破坏阶段曲线骤降,表明完整试件的弹性及脆性较为明显,峰值应力为139.4 MPa。而预制裂隙对岩石试样的强度与变形特性产生了明显的影响。加载起始阶段应力与完整岩体接近,但在弹性阶段,由于预制裂纹的存在,应力显著降低,且应力曲线有着明显的波动,峰值应力60.6 MPa,较完整岩体下降了56.5%。
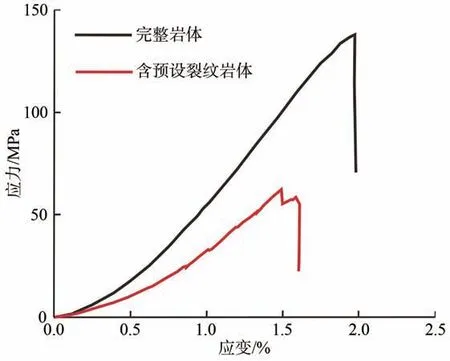
图4 岩体应力应变曲线
在加载过程中记录了所有试件裂纹尖端所在物理覆盖的平均应变,结果如图5所示。根据裂纹可以看出,在计算小于195时步前(A区),裂纹尖端平均应变较大,而从195步到260步之间(B区),裂纹尖端平均应变迅速降低,而后又区域稳定(C区)。根据对裂纹的类型进行了划分,具体裂纹类型可分为张拉裂纹和剪切裂纹。而单轴压缩岩体在垂直于最大主应力方向主要为拉伸状态,这也表明该类型预制裂纹起始时剪切裂纹最后演变为张拉型裂纹。
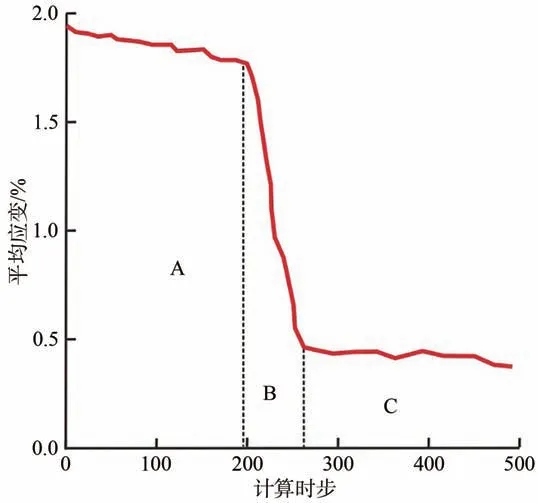
图5 裂纹尖端平均应变
3 结论
1)理论分析了数值流形法中覆盖位移原理及函数表达,将块体单元破坏过程中的数学网格、物理网格以及物理覆盖的变化特征进行了系统描述,为引入破坏本构模型奠定了基础。
2)将摩尔库伦准则引入数值流形法中,规定覆盖中最大主应力、最大剪应力以及块体周边现有的裂纹尖端情况,确定其开裂性质以及开裂发生的方向和位置,开裂面在一个时步内贯穿一个流形单元,并考虑单元破裂过程中的能量损耗。
3)通过单轴压缩试验验证了该破坏本构的使用性,模拟结果表明该模型能够较为准确地反映岩体的破坏特征。预制裂隙对岩体试样的强度与变形特性产生了明显的影响。起始阶段应力与完整岩体接近,但在弹性阶段,应力显著降低,且应力曲线有着明显的波动,峰值应力较完整岩体下降显著。
