Research on Unbounded Parallel-Batch Scheduling with Jobs Having Set-Up Times

(School of Mathematics and Statistics,Zhengzhou University,Zhengzhou 450001,China)

Abstract: We study the scheduling on an unbounded parallel-batch machine with jobs having set-up times to minimize a regular objective function which is either of the sumform or of the max-form.As we know,in the existing literature,the research about parallel-batch scheduling does not consider the set-up times of jobs.However,the set-up times of jobs are widely presented in practical applications.Each job considered in this paper has a set-up time.The set-up time of each batch is equal to the maximum set-up time of all jobs contained in the batch,and the processing time of each batch is equal to the longest processing time of the jobs contained in the batch.Depending on the different definitions of the completion time of a job,we consider two types of jobs: batch jobs and drop-line jobs.For batch jobs,the completion time of a job is given by the completion time of the batch containing this job.For drop-line jobs,the completion time of a job is given by the starting time of the batch containing this job plus the processing time of this job.In this paper,we give pseudo-polynomial time algorithms for the above scheduling problems in which the jobs have agreeable processing times and set-up times.In addition,when the objective functions are the total weighted completion time,the maximum lateness,and the maximum cost,we present a polynomial time algorithm,respectively.

Keywords: Scheduling;Parallel-batch;Set-up time;Agreeable;Algorithm

§1.Introduction

The parallel-batch scheduling model was first introduced in Lee et al.[4] and was motivated by burn-in operations in semiconductor manufacturing.In this model,a parallel-batch machine is a production line that can handle up tobjobs simultaneously as a batch,wherebis the capacity of the batches,and the processing time of a batch is equal to the longest processing time of the jobs contained in the batch.Following the three-parameter scheduling notation introduced by Graham et al.[3],the scheduling problem on a parallel-batch machine of capacitybwas denoted by p-batch(b)|β|γ,where p-batch(b) represents a parallel-batch machine of capacityb,βrepresents the job characteristics or the feasibility conditions,andγrepresents a regular objective function to be minimized.

Parallel-batch scheduling is a hot topic in the research of scheduling.There are two variants of the parallel-batch scheduling: the unbounded model whereb+∞,and the bounded model whereb＜n.As described in Brucker et al.[1],the unbounded model arises for instance in situations where compositions need to be hardened in kilns,and the kiln is sufficiently large that it does not restrict batch sizes.In this paper,we only study the unbounded parallel-batch scheduling.

Depending on the different definitions of the completion time of a job,we consider two types of jobs in this paper: batch jobs and drop-line jobs.For batch jobs,the completion time of a job is given by the completion time of the batch containing this job.Then the corresponding unbounded parallel-batch scheduling problem is denoted by p-batch(+∞)|batch,β|γ.For dropline jobs,the completion time of a job is given by the starting time of the batch containing this job plus the processing time of this job.Then the corresponding unbounded parallel-batch scheduling problem is denoted by p-batch(+∞)|drop-line,β|γ.

Parallel-batch scheduling was widely studied in the literature.But,as we know,in the existing literature,the research about parallel-batch scheduling does not consider the set-up times of jobs.However,the set-up times of jobs are widely presented in practical applications.In this paper,we study the scheduling on an unbounded parallel-batch machine with jobs having set-up times.In the problem,we havenjobsJ1,J2,...,Jn.Each jobJjhas a set-up timesj.This implies that each batch has a set-up time before the batch are processed.The set-up time of each batch is equal to the maximum set-up time of all jobs contained in the batch.Figure 1 displays the structure of a feasible scheduleπin whichs(Bi) denote the set-up time of batchBifori1,2,...,n.In the following,we only review some related achievements.

Figure 1 A feasible schedule π.

For problem p-batch(+∞)|batch|γ,Brucker et al.[1]showed that the problem withγLmaxis solvable inO(n2) time and the problem withγ∑wjCjis solvable inO(nlogn) time.They further proved that the problem with∑wjUj,∑wjTj}is binary NP-hard and the problem with arbitraryγis solvable inO(n2∑pj) time.For the feasibility problem p-batch(+∞)|batch|fmax≤Q,wherefmaxis a max-form regular objective function to be minimized andQis a non-negative integer,they presented anO(n2+nlog∑pj)-time algorithm.As a result,problem p-batch(+∞)|batch|fmaxcan be solved in polynomial time by binary search for the feasibility problem.However,this is not a strongly polynomial-time algorithm.Geng and Yuan [2] further showed that the problem withγfmaxis solvable in strongly polynomial time.

For problem p-batch(+∞)|drop-line|γ,the schedule in which all jobs are processed as a single batch starting at time 0 is optimal.Thus,problem p-batch(+∞)|drop-line|γis trivial.However,when the jobs have set-up times,problem p-batch(+∞)|drop-line,sj|γbecomes difficult.

In this paper,we study the scheduling on an unbounded parallel-batch machine with jobs having set-up times to minimize a regular objective function which is either of the sum-form or of the max-form.Since problem p-batch(+∞)|batch|∑fjis binary NP-hard,we will focus our attention on the special version in which the jobs have agreeable processing times and set-up times,i.e.,pi ＜pjimpliessi ≤sj.Letβ*{batch,drop-line}.Then we have the following scheduling problems

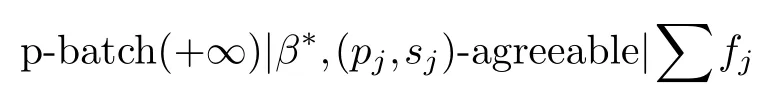
and

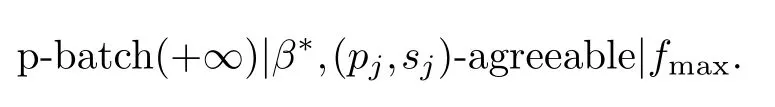
For the above scheduling problems,by borrowing some techniques presented in Brucker et al.[1],we will present some dynamic programming algorithms.

The paper is organized as follows.In section 2,we introduce some notations used in this paper and a fundamental lemma.In section 3,for problem p-batch(+∞)|β*,(pj,sj)-agreeable|∑fj,whereβ*{batch,drop-line},we present a pseudo-polynomialO(n2∑(sk+pk))-time algorithm,respectively.When ∑fj∑wjCj,we present anO(nlogn)-time algorithm,respectively.In section 4,for problem p-batch(+∞)|β*,(pj,sj)-agreeable|fmax,whereβ*{batch,drop-line},we present a pseudo-polynomialO(n2∑(sk+pk))-time algorithm,respectively.WhenfmaxLmax,we present anO(n2)-time algorithm,respectively.Furthermore,we obtained that the problem of minimizingfmaxcan be solved in polynomial time.

§2.Preliminaries

We study the problem of schedulingnindependent jobsJ1,J2,...,Jnon an unbounded parallel-batch machine with jobs having set-up times to minimize a regular objective function.Suppose that all jobs and the machine are available from time zero.Each jobJjhas a processing timepj,a set-up timesj,a due datedj,a weightwj,and a cost functionfj(·),where each functionfj(·) is regular,i.e.,fj(·) is a nondecreasing function.Without loss of generality,we assume that all the job parameterspj,sj,dj,wjare nonnegative and integral.A batch is defined to be a subset of thenjobsJ1,J2,...,Jn.Given a batchB,the processing time ofBis defined to bep(B)max{pj:Jj B}and the set-up time ofBis defined to bes(B)max{sj:Jj B}.In this paper,a feasible scheduleπcan be denoted by a batch sequence (B1,B2,...,Br) which forms a partition of thenjobsJ1,J2,...,Jn.Moreover,the starting timeS(Bk)S(Bk,π) and the completion timeC(Bk)C(Bk,π) of batchBkinπare defined to be

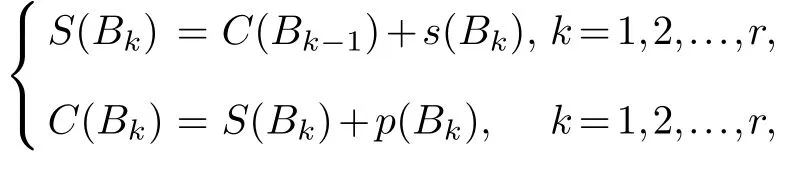
whereB0is a dummy batch withC(B0)0.For each jobJj(j1,2,...,n),we may suppose that jobJjis contained in batchBinπ.Then the starting time of jobJjinπis given bySj(π)S(B,π) and the completion timeCj(π) of jobJjinπis given by

In this paper,we assume that the jobs have agreeable processing times and set-up times,i.e.,pi ＜pjimpliessi ≤sj.This implies that we can re-index thenjobs inO(nlogn) time so that

Then we callσ(B1,B2,...,Br) a SPT-batch schedule,if for any two indicatorsiandj,i＜jimpliesCi(σ)≤Cj(σ).We can obtain the following result which is similar to Lemma 1 in Brucker et al.[1].

Lemma 2.1.For problem p-batch(+∞)|β*,(pj,sj)-agreeable|γ,where β*{batch,drop-line}and γ is a regular objective function to be minimized,there exists an optimal schedule which is also a SPT-batch schedule.

§3.Minimizing ∑fj

In this section,we study problem

whereβ*{batch,drop-line}.According to Lemma 2.1,for the two scheduling problems,we present a forward dynamic programming algorithm,respectively.

LetFj(t) be the minimum objective value for SPT-batch schedules containing the firstjjobsJ1,J2,...,Jjsubject to the condition that the last batch completes at timet.GivenFj(t) and any SPT-batch schedule corresponding to this value,the last batchBis given by{Ji+1,...,Jj}for someiwith 0≤i＜j.From the fact that the processing time of batchBisp(B)maxi+1≤k≤j{pk}pjand the set-up time of batchBiss(B)maxi+1≤k≤j{sk}sj,we can obtain the following dynamic programming algorithm.

Algorithm I.

Theorem 3.1.Problem p-batch(+∞)|β*,(pj,sj)-agreeable|∑fj,where β*{batch,drop-line},can be solved by Algorithm I in O(n2P)time.

For the problem of minimizing the total weighted completion time,i.e.,

whereβ*{batch,drop-line},we present a backward dynamic programming algorithm inO(nlogn) time,respectively.

Algorithm II.

§4.Minimizing fmax

In this section,we study problem

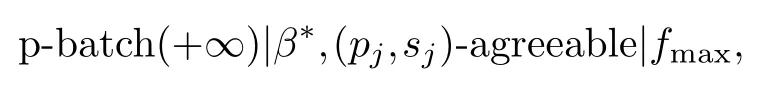
whereβ*{batch,drop-line}.

According to Lemma 2.1,for the two scheduling problems,we present a forward dynamic programming algorithm,respectively.

Similar to section 3,we still useFj(t) to denote the minimum objective value for SPT-batch schedules containing the firstjjobsJ1,J2,...,Jjsubject to the condition that the last batch completes at timet.GivenFj(t) and any SPT-batch schedule corresponding to this value,the last batchBis given by{Ji+1,...,Jj}for someiwith 0≤i＜j.From the fact that the processing time of batchBisp(B)pjand the set-up time of batchBiss(B)sj,we can obtain the following dynamic programming algorithm.

Algorithm III.

Theorem 4.1.Problem p-batch(+∞)|β*,(pj,sj)-agreeable|fmax,where β*{batch,drop-line},can be solved by Algorithm III in O(n2P)time.

For the problem of minimizing the maximum lateness,p-batch(+∞)|β*,(pj,sj)-agreeable|Lmax,whereβ*{batch,drop-line},we present a backward dynamic programming algorithm inO(n2)time,respectively.

LetFjbe the minimum objective value for SPT-batch schedules containing the lastn-j+1 jobsJj,Jj+1,...,Jn.GivenFjand any SPT-batch schedule corresponding to this value,the first batchB′is given by{Jj,...,Jk-1}for somekwithj ＜k ≤n+1.Then we have that the processing time of batchB′isp(B′)pk-1and the set-up time of batchB′iss(B′)sk-1.When batchB′is inserted at the start of a schedule for jobsJk,...,Jn,the maximum lateness of jobsJk,...,Jnincreases by (sk-1+pk-1).Then we present the following dynamic programming algorithm.

Algorithm IV.

The optimal value is equal toF1and the corresponding optimal schedule can be found by backtracking.In the preprocessing step,we can calculate and store the values maxj≤i≤k{sk+pk-di}or maxj≤i≤k{sk+pi-di}forj1,2,...,nandk1,2,...,ninO(n2) time.Note that,each iteration requiresO(n) time.Thus,Algorithm IV runs inO(n2) time.Thus,we can obtain the following theorem.

Theorem 4.2.Problem p-batch(+∞)|β*,(pj,sj)-agreeable|Lmax,where β*{batch,drop-line},can be solved by Algorithm IV in O(n2)time.

For the feasibility problem p-batch(+∞)|β*,(pj,sj)-agreeable|fmax≤Q,we present a polynomial time algorithm as follows.For each jobJj,j1,2,...,n,its deadline can be determined inO(log∑(sj+pj)) time by binary search.By treating the deadlines of jobs as due dates,we use Algorithm IV to minimizeLmax.IfLmax≤0,there exists a schedule such thatfmax≤Q;otherwise,no such schedule exists.Thus,the feasibility problem p-batch(+∞)|β*,(pj,sj)-agreeable|fmax≤Qcan be solved inO(n2+nlog∑(sj+pj))time.This implies that problem p-batch(+∞)|β*,(pj,sj)-agreeable|fmaxcan be solved in polynomial time by binary search for the feasibility problem.