A Sufficient Condition for Networks to be n-Neighbor d-Diagnosable under the Comparison Model

(School of Mathematics and Computer Science,Shanxi Normal University,Taiyuan 030031,China)

Abstract: Diagnosability of multiprocessor systems is an important research topic.The system and an interconnection network have an underlying topology,which is usually presented by a graph.In 2012,Peng et al.proposed a metric for fault diagnosis of the graph,namely,the n-neighbor diagnosability that restrains every fault-free node to contain at least n fault-free neighbors.It is difficult to get the n-neighbor diagnosability of the graph from the definition of the n-neighbor diagnosability.Afterwards,some sufficient and necessary conditions are given.It is also difficult to find the n-neighbor diagnosability of the graph from those results.In this paper,we show some new sufficient conditions for the graph to be n-neighbor d-diagnosable under the MM* model.It improves the corresponding result of [Theoretical Computer Science 773 (2019) 107-114].

Keywords: Interconnection network;Connectivity;Diagnosability

§1.Introduction and preliminaries

A multiprocessor system and an interconnection network (network for short) have an underlying topology,which is usually represented by a graphG(V,E),whereVrepresents processors andErepresents communication links between processors.Since some processors may fail in the system,processor fault identification plays an important role.The identification process of faulty processors is called the diagnosis of the system.Several diagnosis models were proposed to identify the faulty processors.One of the most commonly used is the comparison diagnosis model(MM model),proposed by Maeng and Malek[8].In the MM model,a node sends the same task to two of its neighbors,and then compares their responses.The MM* is a special case of the MM model,where each node must test all pairs of its neighbors in the system.In 2012,Peng et al.[9] proposed a metric for fault diagnosis of the system,namely,then-neighbor diagnosability (also called then-good-neighbor conditional diagnosability),which requires that every fault-free node has at leastnfault-free neighbors.Numerous studies have investigated then-neighbor diagnosability under the MM model or the MM* model (see [2–4,6–15,17–24]).

In this paper,G(V,E) denotes an undirected simple graph.Given a nonempty vertex subsetV ′ofV,the subgraph induced byV ′inG,denoted byG[V ′],is a graph,whose vertex set isV ′and the edge set is the set of all the edges ofGwith both endpoints inV ′.The degreedG(v) of a vertexvis the number of edges incident withv.The minimum degree of a vertex inGis denoted byδ(G).For any vertexv,we define the neighborNG(v) ofvinGto be the set of vertices adjacent tovinG.LetS ⊆V.We useNG(S) to denote the set∪vSNG(v)S.LetGbe connected.LetF1andF2be two distinct subsets ofV,and the symmetric difference betweenF1andF2is

ForX ⊆V,G-Xdenotes the subgraph ofGobtained by removing all the vertices ofXtogether with the edges incident with them fromG.For graph-theoretical terminology and notation not defined here,we follow [1].

LetG(V,E) be connected.For convenience,a subsetF ⊆Vis called afaulty setofG.A faulty setF ⊆Vis called ann-neighbor faulty setif|N(v)∩(VF)|≥nfor every vertexvinVF.Ann-neighbor cutofGis ann-neighbor faulty setFsuch thatG-Fis disconnected.Gis said to ben-neighbor connectedifGhas ann-neighbor cut.LetGben-neighbor connected.The minimum cardinality of ann-neighbor cut is said to be then-neighbor connectivityofG,denoted byκ(n)(G).

The MM model was first proposed by Malek and Maeng [8].In the MM model,a processor sends the same task to a pair of distinct neighbors and then compares their responses to diagnose a systemG(V(G),E(G)).The comparison scheme ofGis a multigraph,denoted byM(V(G),L),whereLis the labeled-edge set.Alabeled edge (u,v)w Lrepresents a comparison in which two verticesuandvare compared by a vertexw,which impliesuw,(G).The collection of all comparison results inM(V(G),L) is called thesyndromeof the diagnosis,denoted byσ.If the comparison (u,v)wdisagrees,thenσ(u,v)w1.Otherwise,σ(u,v)w0.Hence,a syndrome assigns a valueito each edge (u,v)w L,wherei0 or 1.Sengupta and Dahbura proposed the MM* model [2].It is a special case of the MM model.In the MM*model,each node must test all the pairs of its adjacent nodes,i.e.,if(G),then (u,v)w L.The set of all faulty processors in the system is called the faulty set of the system.This can be any subset ofV(G).For a given syndromeσ,a set of verticesF ⊆V(G) is said to beconsistent with σwhenσ(u,v)w1 if and only if at least one ofuandvis in F,for any (u,v)w Lwith.Letσ(F) denote the set of all syndromes whichFis consistent with.LetF1andF2be two distinct sets inV(G).Ifσ(F1)∩σ(F2)Ø,we say (F1,F2) is adistinguishable pair;otherwise,(F1,F2) is anindistinguishable pair.

A systemG(V,E) isn-neighbor d-diagnosableunder the MM*model if and only if(F1,F2) is distinguishable for each distinct pair ofn-neighbor setsF1andF2ofVwith|F1|≤dand|F2|≤d.Then-neighbor diagnosability dn(G) ofGis the maximum value ofdsuch thatGisn-neighbord-diagnosable under the MM*model.In particular,d1(G) is said to be thenature diagnosabilityofGunder the MM*model.

In Fig.1,letF1{2},F2{4}.Note thatσ(2,3)11 is consistent withF1andσ(2,3)10 is consistent withF2.Therefore,(F1,F2) is distinguishable.

Fig.1 An example of a distinguishable pair (F1,F2).

It is difficult to get then-neighbor diagnosability of a system from this definition.Afterwards,the following sufficient and necessary conditions are given [23].

A systemG(V,E) isn-neighbord-diagnosable under the MM*model if and only if each distinct pair ofn-neighbor setsF1andF2ofVwith|F1|≤dand|F2|≤dsatisfies one of the following conditions.(1) There are two vertices(F1∪F2) and there is a vertex1△F2such thatand.(2) There are two vertices1F2and there is a vertex(F1∪F2) such thatand.(3) There are two vertices2F1and there is a vertex(F1∪F2) such thatand.

It is also difficult to find then-neighbor diagnosability of a system from the above theorem.In this paper,I give a new sufficient condition.

LetGbe ann-neighbor connected graph with a perfect matching,with1,and letHbe a connected subgraph ofGwithδ(H)nsuch that|V(H)|is minimum andN(V(H)) is a minimumn-neighbor cut ofG.If|V(G)|＞2|F1∪F2|for each distinct pair ofn-neighbor faulty setsF1andF2ofGwith|F1|≤κ(n)(G)+|V(H)|-1 and|F2|≤κ(n)(G)+|V(H)|-1,then then-neighbor diagnosabilitydn(G) isκ(n)(G)+|V(H)|-1 under the MM*model.

A 1-neighbor connected graphGissuper1-neighbor connectedifG-Fhas a component of order 2 for every minimum 1-neighbor cutFofG.A super 1-neighbor connected graphGis|F|two super1-neighborifG-Fhas two components for every minimum 1-neighbor cutFofG.

In [21],Wang and Wang gave the following theorem.

Theorem A([21]).Let G be an n-good-neighbor connected graph,and let H be a connected subgraph of G with δ(H)n such that it contains V(G)as least as possible,and N(V(H))is a minimum n-good-neighbor cut of G,and let H′ be a connected subgraph of G with δ(G)n such that it contains V(G)as least as possible.If V(H*)faulty subsets F1and F2of G with |F1|≤κ(n)(G)+|V(H′)|-2and |F2|≤κ(n)(G)+|V(H′)|-2,then κ(n)(G)+|V(H′)|-2≤tn(G)≤κ(n)(G)+|V(H)|-1under the MM* model.

In this paper,we show the following results.It improves the corresponding result of [21].

LetGbeκ(1)(G) two super 1-neighbor connected and letBbe a subgraph ofGsuch that|V(B)|2 andN(V(B)) is a minimum 1-neighbor cut ofG.Let (F1,F2) be each distinct pair of 1-neighbor faulty sets ofGwith|F1|≤κ(1)(G)+1 and|F2|≤κ(1)(G)+1,and letW ⊆V(G)(F1∪F2) be the set of isolated vertices inG[V(G)(F1∪F2)].If|W|+|F1∪F2|+2＜|V(G)|,then the nature diagnosability ofGisκ(1)(G)+1 under the MM*model.

§2.Sufficient conditions for networks to be n-neighbor d-diagnosable

Firstly,we give an existing result Theorem 5.1 of [23]).

Theorem 2.1.([23]) A system G(V,E)is n-neighbor d-diagnosable under the MM* model if and only if each distinct pair of n-neighbor sets F1and F2of V with |F1|≤d and |F2|≤d satisfies one of the following conditions.(1) There are two vertices u,w V (F1∪F2)and there is a vertex v F1△F21F2and there is a vertex w V (F1∪F2)2F1and there is a vertex w V (F1∪F2)

Fig.2 Illustration of a distinguishable pair (F1,F2) under the MM* model.

Theorem 2.2.Let G be κ(1)(G)two super1-neighbor connected and let B be a subgraph of G such that |V(B)|2and N(V(B))is a minimum1-neighbor cut of G.Let(F1,F2)be each distinct pair of1-neighbor faulty sets of G with |F1|≤κ(1)(G)+1and |F2|≤κ(1)(G)+1,and let W ⊆V(G)(F1∪F2)be the set of isolated vertices in G[V(G)(F1∪F2)].If|W|+|F1∪F2|+2＜|V(G)|,then the nature diagnosability of G is κ(1)(G)+1under the MM* model.

Proof.Since|W|+|F1∪F2|+2＜|V(G)|for each distinct pair of 1-neighbor faulty sets ofGwith|F1|≤κ(1)(G)+1 and|F2|≤κ(1)(G)+1,we have that

LetF1andF2be a distinct pair of 1-neighbor faulty sets ofGwith|F1|≤κ(1)(G)+1 and|F2|≤κ(1)(G)+1.LetW ⊆V(G)(F1∪F2)be the set of isolated vertices inG[V(G)(F1∪F2)],and letHbe the subgraph induced by the vertex setV(G)(F1∪F2∪W).

Next,we prove thatd1(G)≥κ(1)(G)+1.By the definition of 1-neighbor diagnosability,it is sufficient to show thatGis 1-neighbor (κ(1)(G)+1)-diagnosable.

Suppose,on the contrary,that there are two distinct 1-neighbor faulty setsF1andF2ofGwith|F1|≤κ(1)(G)+1 and|F2|≤κ(1)(G)+1,but the pair (F1,F2) does not satisfy any one condition in Theorem 2.1.Without loss of generality,suppose thatF2F1/Ø.

SinceV(G)V(H)∪W ∪(F1∪F2) and,by the hypothesis,|W|+|F1∪F2|+2＜|V(G)|,we have that|V(H)|＞2.Therefore,V(H)/Ø.

LetF1∩F2Ø.ThenF1△F2F1∪F2.Note thatV(H)/ØandF2F1/Ø.Since there is no edge betweenV(H) and (F1△F2)∪W,Gis not connected,a contradiction.Therefore,F1∩F2.

Since there is no edge betweenV(H) andF1△F2,F1is a vertex cut ofG.SinceF1is a 1-neighbor faulty set ofG,we have that every componentHiofHhas|V(Hi)|≥2 and every componentBiofG[W ∪(F2F1)] has|V(Bi)|≥2.Therefore,F1is also a 1-neighbor cut ofG.IfF1F2/Ø,similarly,we can deduce thatF2is also a 1-neighbor cut ofG.Therefore,F1∩F2is a 1-neighbor cut ofGwhenF1F2/Ø.IfF1F2Ø,thenF1⊂F2andWØ.SinceF1F1∩F2is a 1-neighbor faulty set ofG,we have that every componentHiofG[(F2F1)]has|V(Hi)|≥2.Therefore,F1∩F2is a 1-neighbor cut ofGand|F1∩F2|≥κ(1)(G).

Suppose thatWØ.SinceF1is a 1-neighbor faulty set ofG,we have that every componentGiofG[(F2F1)] has|V(Gi)|≥2.Therefore,

which contradicts|F2|≤κ(1)(G)+1.

Suppose thatW/Ø.We consider the following cases.

Case 1.|F2F1|≥2.In this case,|F2||F2F1|+|F1∩F2|≥2+κ(1)(G),which contradicts|F2|≤κ(1)(G)+1.

Case 2.|F2F1|≤1.SinceF2F1/Ø,|F2F1|≥1 and hence|F2F1|1.

Note thatF2(F2F1)∪(F2∩F1).Since|F1∩F2|≥κ(1)(G),|F2F1|1,|F2|≤κ(1)(G)+1,we have|F1∩F2|κ(1)(G).

SinceGisκ(1)(G) two super 1-neighbor connected,there is a componentPofG-(F1∩F2)such that|V(P)|2.Therefore,

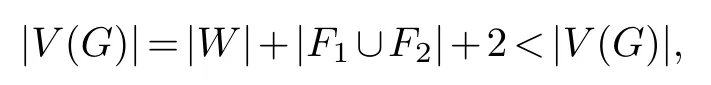
a contradiction.

The following theorem gives an upper bound of then-neighbor diagnosability of a graph.

Theorem 2.3.([21]) Let G(V(G),E(G))be an n-neighbor connected graph,and let H be a connected subgraph of G with δ(H)n such that it contains V(G)as least as possible,and N(V(H))is a minimum n-neighbor cut of G.Then the n-neighbor diagnosability of G is at most κ(n)(G)+|V(H)|-1,i.e.,dn(G)≤κ(n)(G)+|V(H)|-1under the MM* model.

LetG(V(G),E(G)) be ann-neighbor connected graph.LetW ⊆V(G)(F1∪F2) be the set of isolated vertices inG[V(G)(F1∪F2)],and letH*be the subgraph induced by the vertex setV(G)(F1∪F2∪W) for each distinct pair ofn-neighbor faulty setsF1andF2ofGwith|F1|≤κ(n)(G)+|V(H′)|-1 and|F2|≤κ(n)(G)+|V(H′)|-1.

Theorem 2.4.Let G be an n-neighbor connected graph with n/1,and let H be a connected subgraph of G with δ(H)n such that it contains V(G)as least as possible and N(V(H))is a minimum n-neighbor cut of G.Let H′ be a connected subgraph of G with δ(H′)n such that it contains V(G)as least as possible,and let H* be defined as above.If V(H*)/Ø for each distinct pair of n-neighbor faulty sets F1and F2of G with |F1|≤κ(n)(G)+|V(H′)|-1and|F2|≤κ(n)(G)+|V(H′)|-1.Then κ(n)(G)+|V(H′)|-1≤dn(G)≤κ(n)(G)+|V(H)|-1under the MM* model.

Proof.By Theorem 2.3,dn(G)≤κ(n)(G)+|V(H)|-1.

By the definition ofn-neighbor diagnosability,it is sufficient to show thatGisn-neighbor(κ(n)(G)+|V(H′)|-1)-diagnosable.

Suppose,on the contrary,that there are two distinctn-neighbor faulty setsF1andF2ofGwith|F1|≤κ(n)(G)+|V(H′)|-1 and|F2|≤κ(n)(G)+|V(H′)|-1,but the pair (F1,F2) does not satisfy any one condition in Theorem 2.1.Without loss of generality,suppose thatF2F1/Ø.LetW ⊆V(G)(F1∪F2) be the set of isolated vertices inG[V(G)(F1∪F2)],and letH*be the subgraph induced by the vertex setV(G)(F1∪F2∪W).Recall thatV(H*)/Øby the hypothesis.We consider the following cases.

Case 1.n0.By the definition ofH′,|V(H′)|1.Therefore,

and|F2|≤κ(G).Note thatV(H*)/ØandF2F1/Ø.Since the pair (F1,F2) does not satisfy any one condition in Theorem 2.1,by the condition (1) of Theorem 2.1,there is no edge betweenV(G)(F1∪F2) andF1△F2.Thus,F1∩F2is a 0-neighbor cut ofGand|F1∩F2|≥κ(G).

Therefore,

which contradicts|F2|≤κ(G).Therefore,Gis 0-neighborκ(G)-diagnosable andd(G)d0(G)≥κ(G).Combining this with Theorem 2.3,we haved0(G)κ(G).

Case 2.n≥2.

Claim 1.G-F1-F2has no isolated vertex.

Suppose,on the contrary,thatG-F1-F2has at least one isolated vertexx.SinceF1is ann-neighbor faulty set andn≥2,there are at least two vertices2F1such thatu,vare adjacent tox.According to the hypothesis,the pair (F1,F2) does not satisfy any one condition in Theorem 2.1.By the condition(3)of Theorem 2.1,there is at most one vertex2F1such thatuis adjacent tox.So(x)|≤1,a contradiction to the fact thatF1is ann-neighbor faulty set withn≥2.Thus,G-F1-F2has no isolated vertex.This concludes the proof of Claim 1.

Let(G)(F1∪F2).By Claim 1,δ(G-F1-F2)≥1.Since the pair (F1,F2) does not satisfy any one condition in Theorem 2.1,by the condition (1) of Theorem 2.1,for any pair of adjacent vertices(G)(F1∪F2),there is no vertex1△F2such that(G)and(G).It follows thatuhas no neighbor inF1△F2.Asuis an arbitrary vertex inV(G)(F1∪F2),there is no edge betweenV(G)(F1∪F2) andF1△F2.SinceF2F1/ØandF1is ann-neighbor faulty set,δ(G[F2F1])≥nandδ(G-F2-F1)≥n.Since bothF1andF2aren-neighbor faulty sets,and there is no edge betweenV(G)(F1∪F2) andF1△F2,F1∩F2is ann-neighbor cut ofGand|F1∩F2|≥κ(n)(G).Therefore,

which contradicts|F2|≤κ(n)(G)+|V(H′)|-1.Therefore,Gisn-neighbor (κ(n)(G)+|V(H′)|-1)-diagnosable anddn(G)≥κ(n)(G)+|V(H′)|-1.Combining this with Theorem 2.3,

By Theorem 2.4,we have the following corollary.

Corollary 2.1.Let G be an n-neighbor connected graph with n1,and let H be a connected subgraph of G with δ(H)n such that |V(H)| is minimum and N(V(H))is a minimum nneighbor cut of G.Let H* be defined as above.If V(H*)1and F2of G with |F1|≤κ(n)(G)+|V(H)|-1and |F2|≤κ(n)(G)+|V(H)|-1,then dn(G)κ(n)(G)+|V(H)|-1under the MM* model.

A component of a graphGisoddaccording as it has an odd number of vertices.We denote byo(G) the number ofodd componentsofG.

Lemma 2.1.([1]) A graph G(V,E)has a perfect matching if and only if o(G-S)≤|S| for all S ⊆V.

Theorem 2.5.Let G be an n-neighbor connected graph with a perfect matching,with n1,and let H be a connected subgraph of G with δ(H)n such that |V(H)| is minimum and N(V(H))is a minimum n-neighbor cut of G.If |V(G)|＞2|F1∪F2| for each distinct pair of n-neighbor faulty sets F1and F2of G with |F1|≤κ(n)(G)+|V(H)|-1and |F2|≤κ(n)(G)+|V(H)|-1,then the n-neighbor diagnosability dn(G)is κ(n)(G)+|V(H)|-1under the MM* model.

Proof.By Theorem 2.3,dn(G)≤κ(n)(G)+|V(H)|-1.

SinceGhas a perfect matching,by Theorem 2.1,

Note that|V(G)||F1∪F2|+|W|+|V(H*)|,whereH*is defined as above.Since|V(G)|＞2|F1∪F2|,V(H*)/Øholds.By Corollary 2.1,dn(G)κ(n)(G)+|V(H)|-1.

§3.Application

Firstly,we give the bubble-sort star graph.

In the permutation

For convenience,we denote the permutation

byp1,p2,...,pm.Every permutation can be written by a product of cycles [5].For example,

Specially,

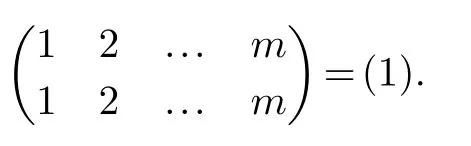
The productστof two permutations is the composition functionτfollowed byσ,that is,(12)(13)(132).For terminology and notation not defined here we follow [5].

Let[m]{1,2,···,m},and letSmbe the symmetric group on[m]containing all permutationspp1p2···pmof [m].It is well known that{(1i):2≤i≤m}is a generating set forSm.So{(1,i):2≤i≤m}∪{(i,i+1):2≤i≤m-1}is also a generating set forSm.Them-dimensional bubble-sort star graphBSmis the graph with vertex setV(BSm)Smin which two verticesu,vare adjacent if and only ifuv(1,i),2≤i≤m,oruv(i,i+1),2≤i≤m-1.It is easy to see from the definition thatBSmis a (2m-3)-regular graph onm! vertices.

A graphGis said to bek-regular if for any vertexv,dG(v)k.

Lemma 3.1.([1]) Let k ≥0be an integer.Then every k-regular bipartite graph has k edge-disjoint perfect matchings.

Theorem 3.1.([18]) For m≥5,the bubble-sort star graph BSm is(4m-8)two super 1-neighbor connected.

We give a simple proof of the following theorem.

Theorem 3.2.([16]) Let m≥5.Then the nature diagnosability of the bubble-sort star graph BSm is4m-7under the MM* model.

Proof.By Theorem 3.1,BSmis (4m-8) two super 1-neighbor connected.LetB{(1),(1 2)}.SinceBSmis bipartite,N({(1)})∩N({(1 2)})Øand|N(B)|4m-8κ(1)(BSm).Therefore,

and henceN(B) is a minimum 1-neighbor cut ofBSm.

LetF1andF2be two distinct 1-neighbor faulty sets ofBSmwith|F1|≤κ(1)(BSm)+1 and|F2|≤κ(1)(BSm)+1.LetW ⊆V(BSm)(F1∪F2) be the set of isolated vertices inBSm[V(BSm)(F1∪F2)].SinceBSmis a regular bipartite graph,by Lemma 3.1,it has a perfect matching.By Lemma 2.1,

Note thatV(BSm)V(H)∪W ∪(F1∪F2).Therefore,

Sincem≥5,16m-28＜m! and 16m-26＜m!.Therefore,

By Theorem 2.2,the nature diagnosability of the bubble-sort star graphBSmis 4m-7 under the MM*model.

Lemma 3.2.([19]) Let BSm be the bubble-sort star graph and A{(1),(1 2),(1 2 3),(1 3)}.If m≥5,F1N(A)and F2A∪N(A),then |F1|8m-22,|F2|8m-18,δ(BSm-F1)≥2,and δ(BSm-F2)≥2.

Theorem 3.3.([19]) For m≥5,the 2-neighbor connectivity of the bubble-sort star graph BSm is8m-22.

By Theorem 3.3 and Lemma 3.2,the graphBSm[A] has minimum degree 2 andN(A) is a minimum 2-neighbor cut ofBSm.SinceBSmis a (2m-3)-regular graph,by Lemma 3.1,BSmhas a perfect matching.SinceBSmis bipartite,|V(BSm[A])|is minimum withδ(BSm[A])2.Sincem!＞2[(8m-22)+4-1+(8m-22)+4-1] whenm≥5,we have|V(BSm)|＞2|F1∪F2|for each distinct pair of 2-neighbor faulty setsF1andF2ofBSmwith|F1|≤(8m-22)+4-1 and|F2|≤(8m-22)+4-1.By Theorem 2.5,we have the following corollary.

Corollary 3.1.([19]) For m≥5,the 2-neighbor diagnosability of the bubble-sort star graph BSm is8m-19under the MM* model.

Them-dimensional hypercubeQmis proposed by Saad and Schultz [12],which is a famous topology structure of an interconnection network for multiprocessor systems.Qmis anm-regular graph whose vertex set is{u1u2···um:ui {0,1}for 1≤i≤m}.Two verticesuu1u2···umandvv1v2···vmare adjacent if and only if there exists exactly a positionj,such thatujvjfor every 1≤j ≤m,i.e.,

Theorem 3.4.([9,12]) Let m≥3and0≤n≤m-2.Suppose that F is a minimum cardinality cut of Qm such that |(x)(Qm)F.Then |F|(m-n)2n.

Theorem 3.5.([7]) Let H be a subgraph of Qm such that δ(H)n.Then |V(H)|≥2n,for0＜n≤m.

Lemma 3.3.([17]) Let A be defined as above,0≤n≤m-3,and let F1(A),F2A∪NQm(A).Then δ(Qm[A])n,|F1|(m-n)2n,δ(Qm-F1)≥n and δ(Qm-F2)≥m-2.

By Lemma 3.1,Qmhas a perfect matching.By Lemma 3.3 and Theorem 3.4,Qm[A] is a connected subgraph ofQmwith minimum degreenandN(A) is a minimumn-neighbor cut ofQm.Since|A|2n,by Lemma 3.3 and Theorem 3.5,|A|is minimum such thatδ(Qm[A]))n.It is easy to verify 2m ＞4((m-n+1)2n-1) whenm≥7 and 0≤n≤m-5.Therefore,|V(Qm)|＞2|F1∪F2|for each distinct pair ofn-neighbor faulty setsF1andF2ofQmwith|F1|≤(m-n+1)2n-1 and|F2|≤(m-n+1)2n-1.By Theorem 2.5,we have the following corollary.

Corollary 3.2.([17]) Let m≥7,0≤n≤m-5and n/1.Then the n-neighbor diagnosability of the m-dimensional hypercube under the MM* model is(m-n+1)2n-1.

The set ofm-dimensional hypercube-like graphs,denoted byHLm,can be recursively defined as follows:

Lemma 3.4.([25]) Let m≥5,0≤n≤m-3.For any Xm HLm,let F ⊆V(Xm).If |F|≤fm(n)-k with0≤k ≤1,then Xm-F has a component with at least2m-|F|-(n+1-k)vertices.

Theorem 3.6.Let Qm be the m-dimensional hypercube.If m≥6,then the nature diagnosability of the m-dimensional hypercube under the MM* model is2m-1.

Proof.By Theorem 3.4,κ(1)(Qm)2m-2.Note thatfm(1)2m-2.LetFbe a minimum 1-neighbor cut ofQm.Then|F|2m-2fm(1).By Lemma 3.4,Qm-Fhas a component with at least (2m-2m) vertices.Note that

Therefore,Qm-Fhas two components and henceQmis (2m-2) two super 1-neighbor connected.

Let0,1},and letA{0m-1X1}.Then|N(A)|2(m-1)2m-2.Therefore,N(A) is a minimum 1-neighbor cut ofQm.

LetF1andF2be a distinct pair of 1-neighbor faulty sets ofQmwith|F1|≤2m-1 and|F2|≤2m-1.By Lemma 3.1,Qmhas a perfect matching.LetW ⊆V(Qm)(F1∪F2)be the set of isolated vertices inQm[V(Qm)(F1∪F2)].By Lemma 2.1,|W|≤o(G-(F1∪F2))≤|F1∪F2|.Therefore,

whenm≥6.By Theorem 2.2,the nature diagnosability ofQmunder the MM*model is 2m-1.

§4.Conclusions

Then-neighbor diagnosability of multiprocessor systems is an important metric.In this paper,we show some sufficient conditions for the network to ben-neighbord-diagnosable under the comparison model.This makes it easier to find then-neighbor diagnosability of the network.