Ergodicity of Bandwidth and Cutwidth on Families of Graphs and Trees

(1.School of Internet Finance and Information Engineering,Guangdong University of Finance,Guangzhou 510000,China;2.School of Mathematical Science,South China Normal University,Guangzhou 510000,China)

Abstract: Bandwidth,cutwidth,cyclic bandwidth,bandwidth sum and cyclic bandwidth sum are well-known indices about optimal labeling of graphs applied in VLSI design,network communications,and other areas involving the graph layout.To design the graphs with the given indices,we need to study the ergodicity.Let F be a set of graphs under consideration and φ an integer-valued function defined on F,namely, φ is an index,such as bandwidth and cutwidth.If there exists a graph GF such that φ(G)x for any integer x in the interval [a,b],where a and b are the minimum and maximum of φ on F,respectively,then φ is said to have ergodicity on F.Let Gn be the set of simple connected graphs with order n and Tn the set of trees with order n.In this paper,we investigate the ergodicity of bandwidth,cutwidth,cyclic bandwidth,the bandwidth sum and cyclic bandwidth sum on Tn and Gn.

Keywords: Ergodicity;Bandwidth;Cutwidth;Cyclic bandwidth;Bandwidth sum

§1.Introduction and preliminaries

LetG(V,E)be a graph of ordern.A bijection fromVonto{1,2,...,n}is called a labeling ofG.

Definition 1.1.Let f be a labeling of G and B(G,f)The bandwidth of G,denoted by B(G),is defined as

A labeling f of G satisfying that B(G,f)B(G)is called an optimal bandwidth labeling of G.Clearly,B(Pn)1,where Pn is a path with order n.

Definition 1.2.Let f be a labeling of G and Bc(G,f)-f(v)|c,where xcmin{x,n-x} for integer x such that0＜x＜n.The cyclic bandwidth of G,denoted by Bc(G),is defined as

A labeling f of G satisfying that Bc(G,f)Bc(G)is called an optimal cyclic bandwidth labeling of G.

Definition 1.3.Let f be a labeling of G and BS(G,f)∑uvE|f(u)-f(v)|.The bandwidth sum of G,denoted by BS(G),is defined as

A labeling f of G satisfying that BS(G,f)BS(G)is called an optimal bandwidth sum labeling of G.Clearly,BS(Pn)n-1.

Definition 1.4.Let f be a labeling of G and BSc(G,f)-f(v)|c.The cyclic bandwidth sum of G,denoted by BSc(G),is defined as

A labeling f of G satisfying that BSc(G,f)BSc(G)is called an optimal cyclic bandwidth sum labeling of G.

For a subsetXofV,let△X.

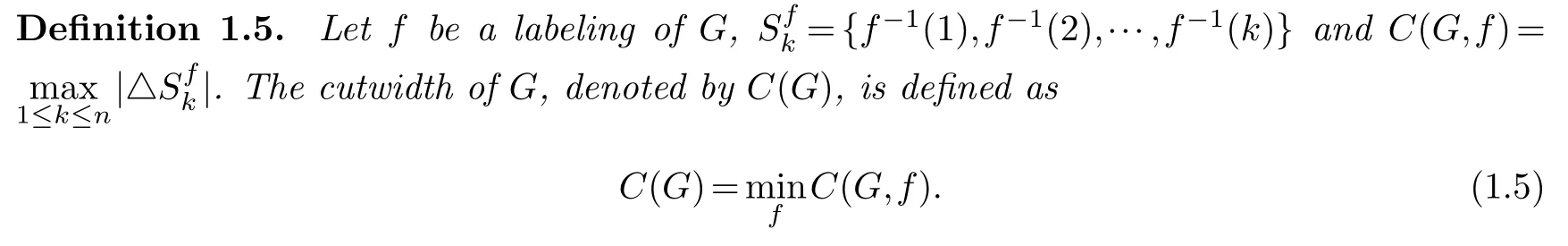
A labeling f of G satisfying that C(G,f)C(G)is called an optimal cutwidth labeling of G.Clearly,C(Pn)1.

Letmbe an integer such that 1≤m≤n.Then,by Definition 1.5,

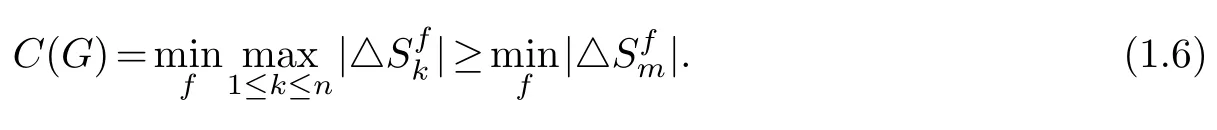
Optimal labeling (embedding) problems for graphs,such as bandwidth,bandwidth sum,cyclic bandwidth,cyclic bandwidth sum and cutwidth,arise from the circuit layout of VLSI designs,data structures,biology,etc [2].But it is well known that these optimal labeling problems are NP-complete[1,7,9].Y.X.Lin,J.J.Yuan and others did a lot of work on calculating the indices on some special classes of graphs (see [1,3–6,10–12]).Reversely,the problems that design the graphs with given indices (such as bandwidth etc) receive attention,which are applied in VLSI design and network communications (see [8,13]).In this paper,we investigate the problem that whether there is a simple graph (tree) whose bandwidth (bandwidth sum,cyclic bandwidth,cyclic bandwidth sum and cutwidth) is equal to an integerk,which is called ergodicity.LetFbe a set of graphs under consideration andφan integer-valued function defined onF,namely,φis an index,such as bandwidth and cutwidth.If there exists a graphsuch thatφ(G)xfor any integer[a,b],whereaandbare the minimum and maximum ofφonF,respectively,then we say thatφhas ergodicity onF.J.X.Hao [10] proved that for any tree,1≤C(T)≤and for any integer[1,],there exists a treeT0such thatC(T0)k.It means that the cutwidth has ergodicity onTn.It is clear that for any,1≤B(G)≤n-1 and 1≤Bc(G)≤In [1] and [11],we can know that for any integer[1,n-1],there exists a simple connected graphsuch thatkand for any integerthere exists a simple connected graphsuch thatk,whereis thekth power of a path(cycle)of ordern.So it follows that the bandwidth and cyclic bandwidth both have ergodicity onGn.In this paper,we prove that the bandwidth has ergodicity onTn,the cutwidth has the ergodicity onGn,but the bandwidth sum and cyclic bandwidth sum do not have ergodicity onTnandGn.

Before presenting the main results of this paper,we shall first introduce some fundamental properties of optimal labeling problems.It is easy to get that if an edge or a vertex is removed from a graphG,then the bandwidth,bandwidth sum,cyclic bandwidth,cyclic bandwidth sum and cutwidth will not be increased.Thus we have the following lemma.

Lemma 1.1.Let G′ be a subgraph of G.Then B(G′)≤B(G),Bc(G′)≤Bc(G),BS(G′)≤BS(G),BSc(G′)≤BSc(G)and C(G′)≤C(G).

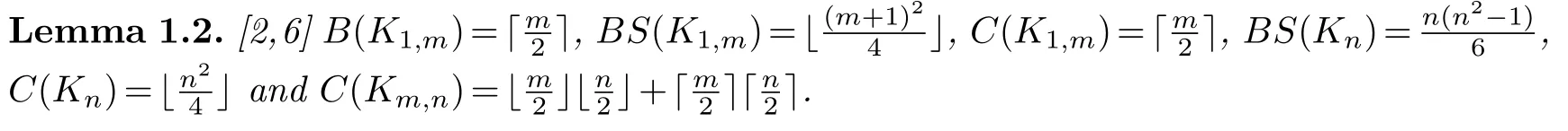
The paper is organized as follows.In section 1,we introduce the definitions,notations,the research background and some basic lemmas.In section 2,we main study the ergodicity on treesTn.In section 3,we consider the ergodicity of bandwidth sum and cyclic bandwidth sum onGn.

§2.Ergodicity on Tn

Lemma 2.1.[1,12] For any tree T,B(T)Bc(T),BS(T)BSc(T).Then,we only need to investigate the ergodicity of bandwidth and bandwidth sum on Tn.

Theorem 2.1.Bandwidth has ergodicity on Tn.

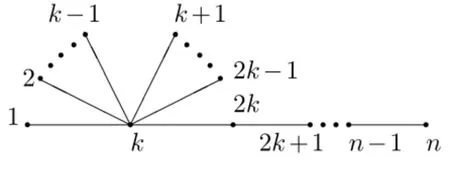
Fig.1 A labeling f0 for T0.

Now,we investigate the ergodicity of bandwidth sum onTn.

Letf0be an optimal cyclic bandwidth sum labeling ofT0.We construct a labelingfforTas follows.

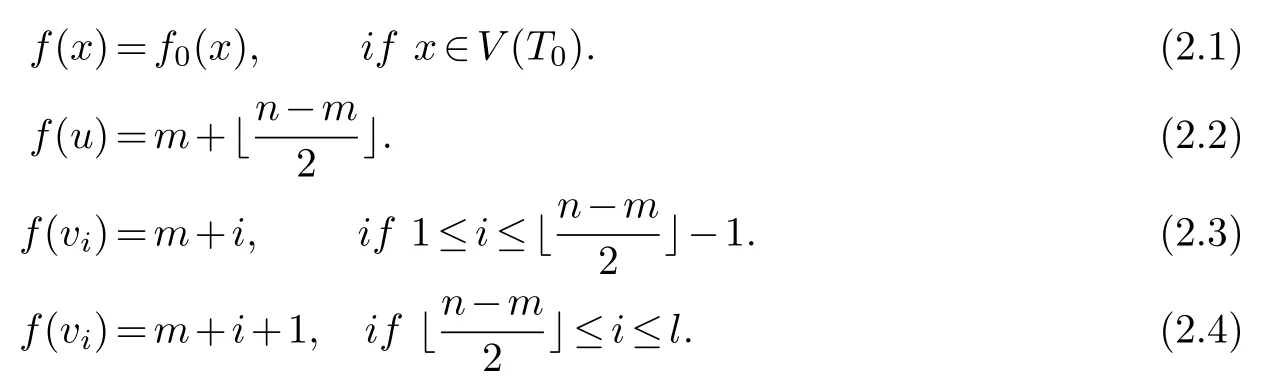
Then we have that

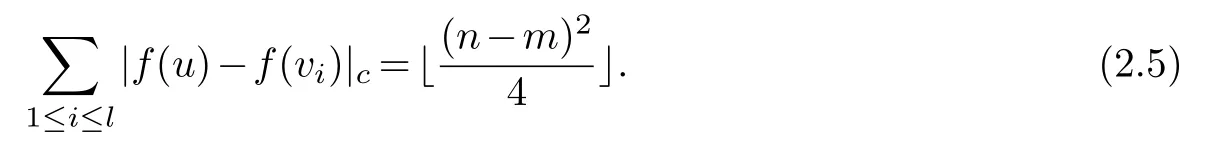
Thus,

So the theorem holds.

§3.Ergodicity on Gn

First,we investigate the ergodicity of bandwidth sum and cyclic bandwidth sum onGn.

Lemma 3.1.(Kn),BSc(Kn-e)BSc(Kn)-

Lemma 3.2.(Kn),BS(Kn-e)BS(Kn)-n+1.

6.Father: The father has an excellent excuse for not protecting his daughter in this tale--he s dead. Other fairy tale heroines suffer from ineffective fathers, such as in Hansel and Gretel and Rumpelstiltskin. Return to place in story.

Proof.On the one hand,letGKn-e(e(Kn)) andfbe an optimal bandwidth sum labeling ofG.Then

Then

On the other hand,letV(G){v1,v2,···,vn}andev1vn.Construct a labelingfforGas follows:

Then,

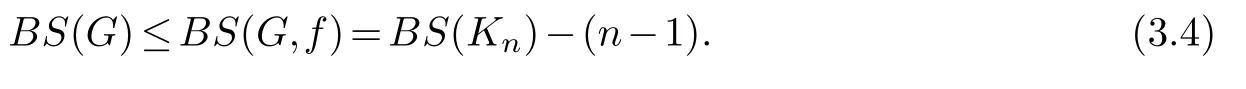
Hence,BS(G)BS(Kn)-(n-1).

Theorem 3.1.For any integer n≥4,bandwidth sum and cyclic bandwidth sum do not have ergodicity on Gn.

Proof.For any,n-1≤BS(G)≤BS(Kn) by the definition of bandwidth sum and by Lemma 1.1.We prove that there does not existsuch thatBS(G)BS(Kn)-1.Suppose thatG/Kn.ThenGis a subgraph ofKn-e.By Lemma 1.1,BS(G)≤BS(Kn-e).By Lemma 3.2,BS(Kn-e)BS(Kn)-n+1.Then,

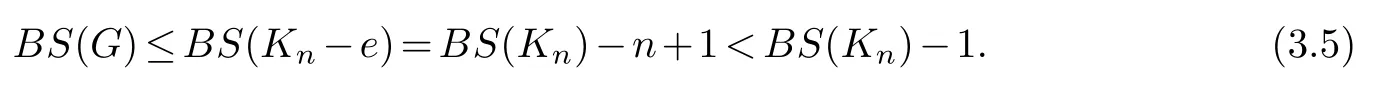
Thus,for any,BS(G)/BS(Kn)-1.

Clearly,for any,n-1≤BSc(G)≤BSc(Kn).We prove that there does not existsuch thatBSc(G)BSc(Kn)-1.Suppose thatG/Kn.ThenGis a subgraph ofKn-e.By Lemma 1.1,BSc(G)≤BSc(Kn-e).By Lemma 3.1,BSc(Kn-e)BSc(Kn).Then,

Thus,for any,BSc(G)/BSc(Kn)-1(n≥4).

Finally,we investigate the ergodicity of cutwidth onGn.

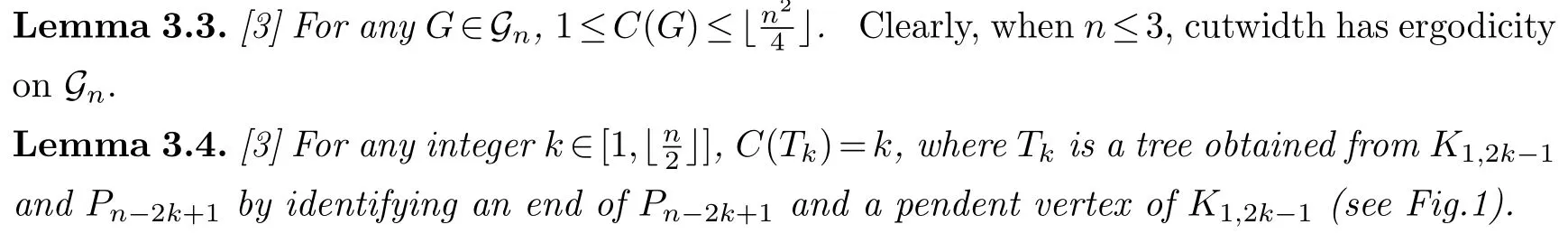
LetSandTbe disjoint subsets ofV(G).We denote the edge subset(G)by [S,T].

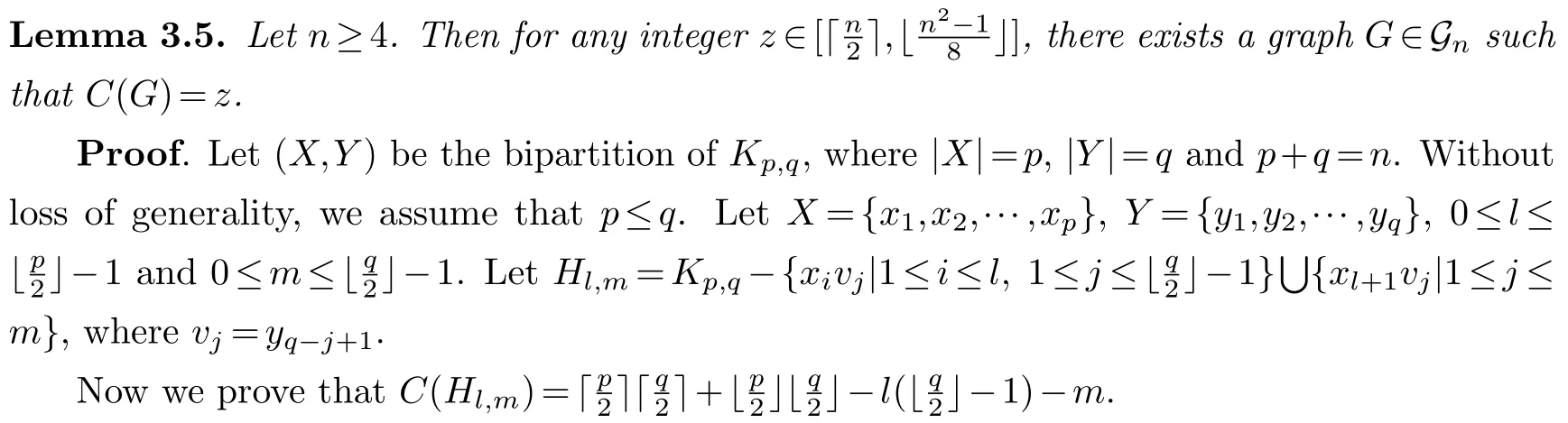
First,we construct a labelingfforHl,mas follows:

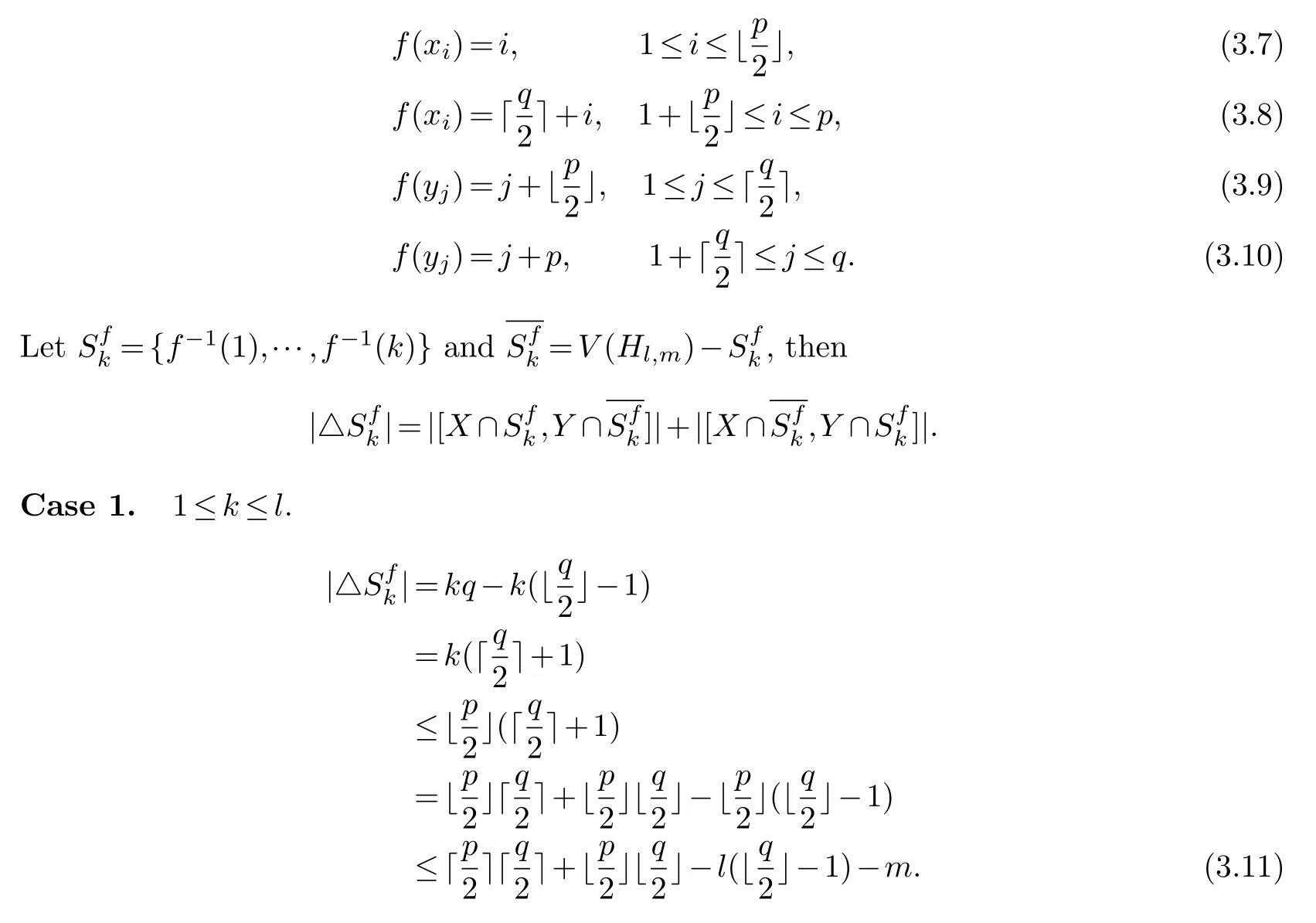
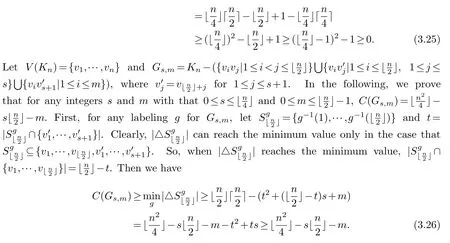
Secondly,we construct a labelingfforGs,mas follows:

Whenn-m+1≤k ≤n,we have that

Thus,

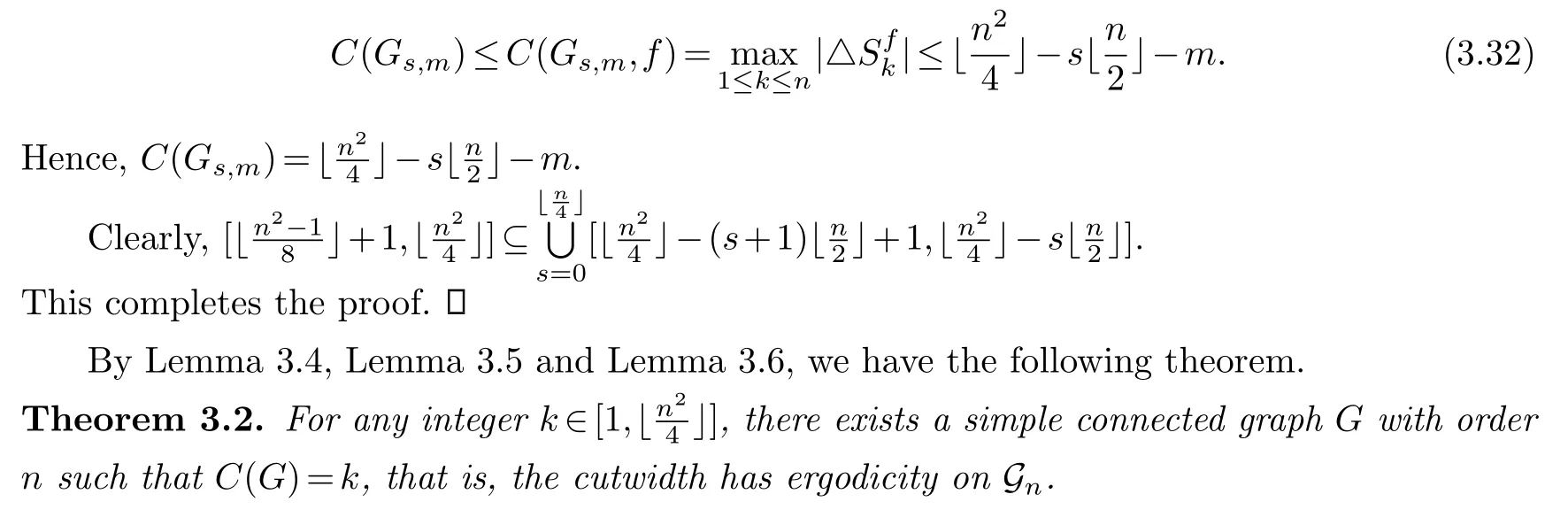
Acknowledgements

Yan Liu is Mr.Yixun Lin’s doctoral student of 2000.This article is to celebrate Mr.Yixun Lin’s 85th birthday.