Forming a Critical Tree with Cutwidth k

(1.School of Mathematics and Statistics,Huanghuai University,Zhumadian 463000,China;2.Zhengzhou Electronic Information Engineering College,Zhenzhou 450007,China)

Abstract: The cutwidth of a graph G is the minimum number of overlap edges when G is embedded into a path Pn.The cutwidth problem for a graph G is to determine the cutwidth of G.A graph G with cutwidth k is k-cutwidth critical if every proper subgraph of G has cutwidth less than k and G is homeomorphically minimal.In this paper,we completely investigated methods of forming a k-cutwidth (k ＞1) critical tree T.

Keywords: Combinatorics;Graph labeling;Cutwidth;Critical tree

§1.Introduction

Graphs in this paper are finite,simple and connected,with undefined notation following [1].A known NP-complete problem for general graphs except trees [6,10],the cutwidth problem for graphs as well as the optimal labeling (or embedding) problems,have significant applications inV LSIdesigns,network communications and others.In particular,the cutwidth is related to a basic parameter,called thecongestion,in designing microchip circuits [2,5,9].Here,a graphGcan be thought of as a model of the wiring diagram of an electronic circuit,with the vertices representing components and the edges representing wires connecting them.When a circuit is laid out on a certain architecture (say a path),the maximum number of overlap wires is the congestion,which is one of major parameters determining the electronic performance.This motivates the cutwidth problem in graph theory practically.Theoretically,the cutwidth is closely connected with other graph-theoretic parameters such as bandwidth,pathwidth and treewidth [3,5,7],among others.

Given a graphG(V(G),E(G)) onnvertices,a labeling ofGis a bijectionf:V(G)→Sn,viewed as an embedding ofGinto the pathPnwith vertices inSn,where consecutive integers are the adjacent vertices andSn{1,2,···,n}.The cutwidth ofGwith respect tofis

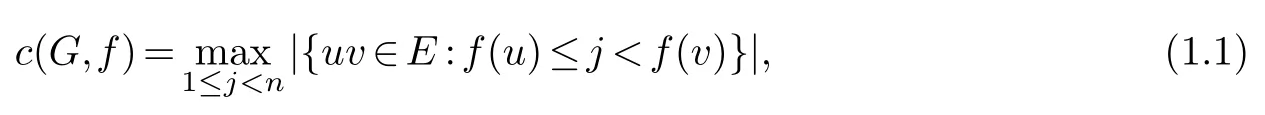
which represents the congestion of the embedding.The cutwidth ofGis defined as

where the minimum is taken over all labelingsf.For a labelingfand any(G),f(v)is called the label ofv.A labelingfattaining the minimum in (2) is an optimal labeling ofG,andf(v) is called an optimal label ofv.For eachiwith 1≤i≤n,letvif-1(i) andSj{v1,v2,···,vj}.Define∇f(Sj){vivh E:i≤j ＜h}and call∇f(Sj) the (edge) cut at[j,j+1].By (1.2),we have

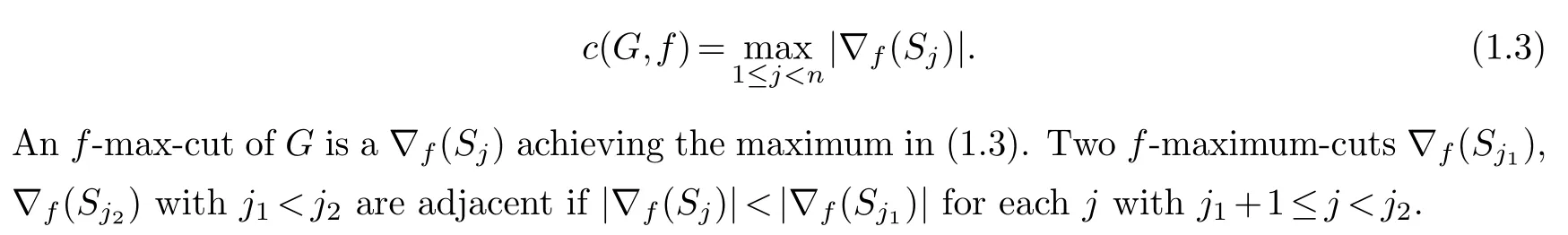
For graphGand integeri≥0,letDi(G)(G):dG(v)i}.Any vertex inD1(G) is called a pendant vertex inG,and any edge incident with a vertex inD1(G)is a pendant edge ofG,andEp(T){vivj:vivjis a pendant edge inG},Vp(T){v:vvi(orvj),vivj Ep(T)}.For(G),letNG(v)(G):(G)}.IfGhas a vertex2(G)withNG(v){v1,v2}andv1v2(G),thenG-v+v1v2,obtained fromG-vby adding a new edgev1v2,is call a series reduction ofG.A graphGis homeomorphically minimal ifGdoes not have any series reductions.A graphGis minimally homeomorphic to a graphHifGis homeomorphic toHandGis homeomorphically minimal.A graphGis calledk-cutwidth critical ifGis homeomorphically minimal withc(G)ksuch that every proper subgraphG′ofGsatisfiesc(G′)＜k.For a treeTwith vertex(T),if min{c(Fi+vvi):vi NT(v)}≥ρ,thenvis called theρ-max-vertex,whereFiis a component ofT-vandρ(ρ＜k) is a positive integer.

Fork ≥1,thek-cutwidth critical graph problem,also called the forbidden subgraph problem of (k-1)-cutwidth graphs,is one of the important contents on the extreme graph theory.The set of the critical graphs with cutwidth at most 3 characterized in Lemma 1.1,and the set of 4-cutwidth critical trees,which consists of 18 elements,have been investigated in [12] and [13].In addition,fork ≥4,Some special methods of constructingk-cutwidth critical trees and nontree graphs were contained in[11–14],respectively.In this paper,new methods of formingk-cutwidth critical trees are verified completely.

By [8],we have

Lemma 1.1.The unique 1-cutwidth critical graph is K2.The only 2-cutwidth critical graphs are K3and K1,3.All 3-cutwidth critical graphs are H1,H2,H3,H4and H5depicted in Fig.1.

Fig.1 The 3-cutwidth critical graphs.

The lemma below follows immediately from definition.

Lemma 1.2.Let G and G′ be graphs.Each of the following holds.

(i)If G′ is a subgraph of G,then c(G′)≤c(G).

(ii)If G′ is homeomorphic to G,then c(G′)c(G).

(iii)For a cut edge e of G,if V1,V2are the vertex sets of two components of G-e,then there is an optimal labeling f* under which the vertices in each of {V1,V2} are labeled consecutively.

The rest of this paper is as follows.In Section 2,some preliminary results are presented.Section 3 summarizes three known methods of constructing ak-cutwidth critical tree.Section 4 is devoted to main results.Remarks are given in Section 5.

§2.Preliminaries

We first introduce two graph operations by Definitions 2.1-2.2.By [13],c(K1,2k-1)k,so we have a convention that ifTis a tree thendT(v)＜2k-1 for any(T) in this paper.

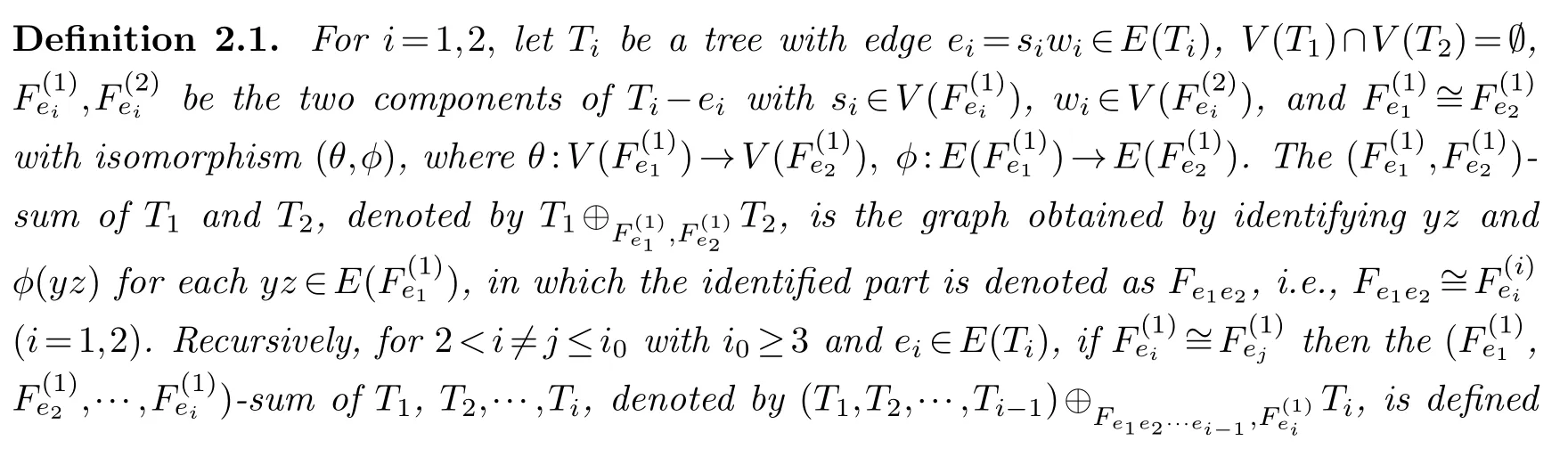
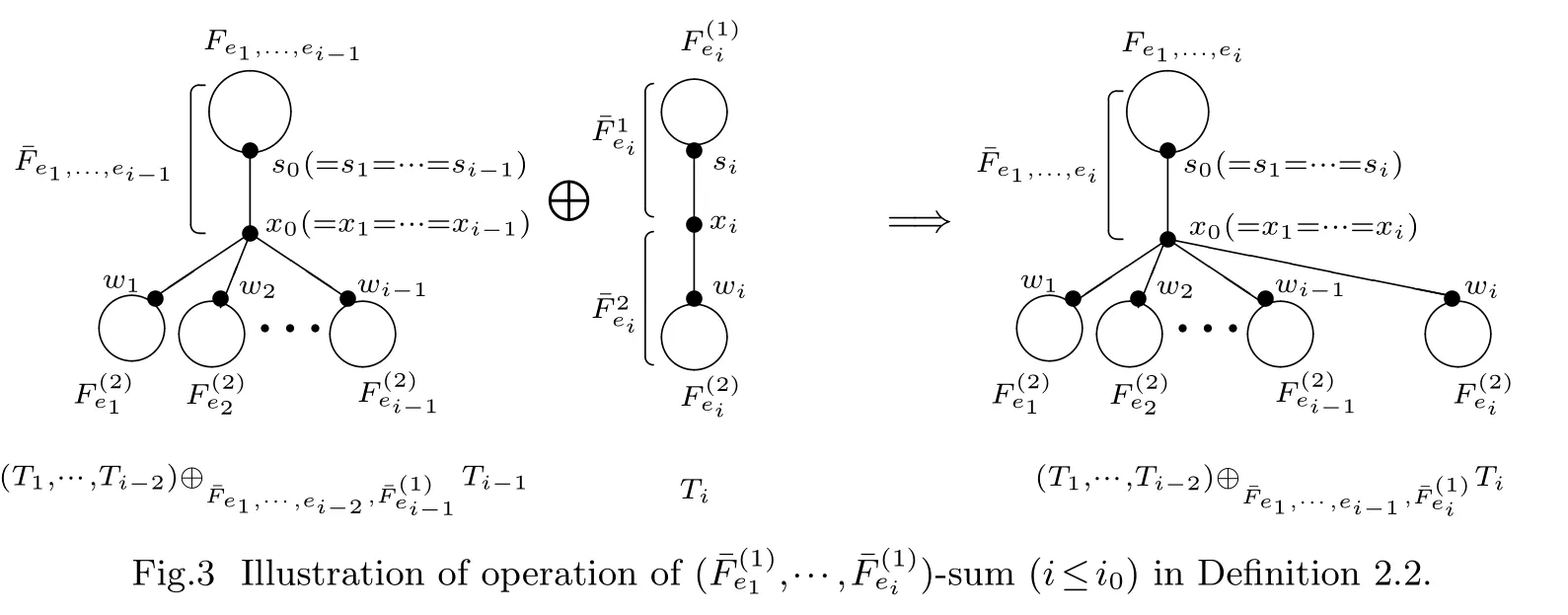
Definition 2.3.Let T(V(T),E(T))be a tree.

(i)For any {v,v1,v2,···,vr}⊆V(T),define T(v;v1,v2,···,vr)as the maximum subtree component of T that contains v but does not contain any of {v1,v2,···,vr} (see an example in Fig.4).

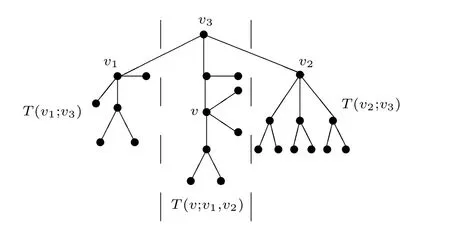
Fig.4 An example of Definition 2.3(i).

(ii)If |V(T)|≥2,then define M(T){T-v:1(T)} to be the family of all maximal proper subtrees of T.

The following Lemma is from [4] and [13].

Lemma 2.1.For a tree T,each of the following holds.

(i)c(T)≤k if and only if every vertex v of degree at least 2 has neighbors v1,v2such that c(T(v;v1,v2))≤k-1.

(ii)c(T)≥k if and only if there exists a nonpendant vertex v such that c(T(v;v1,v2))≥k-1holds for any two neighbors v1,v2of v.

(iii)For1≤i≤3,let Ti be(k-1)-cutwidth with zi D1(Ti).Then TT(z0;T1,T2,T3)is k-cutwidth,where z1z2z3z0.

Lemma 2.3.Let tree T be k-cutwidth critical with |D1(T)|l.Then T has at least l optimal labelings f* under which f*-max-cut ∇(Sj)is unique.

Proof.We first verify the following Claim.

Claim.Any1(T) corresponds to at least an optimal labelingf*under whichf*-max-cut∇(Sj) is unique.

Definition 2.4.Let v0(T)with NT(v0){vr:1≤r ≤r0,r0≥3},Fr be a component of T-v0corresponding to vr NT(v0)and

Similarly,Tis alsok-cutwidth critical ifv0is a strongk-critical vertex inT,omitted here.This completes the proof.

In the sequel,the labelingfdefined in (2.1) is called the labeling by the order (f1,f2,f3)(or (V(F1),V(),V(F3))).

Theorem 2.2.Let T be a k-cutwidth critical tree.Then there is a vertex v0(T)D1(T)such that v0is either k-critical or strong k-critical.

§3.Three known methods

Fork ＞1,a few method of forming specialk-cutwidth critical trees has been found in[12,13],which are contained in Lemmas 3.1-3.3 below,respectively.

Fig.5 Definition of .

§4.Main results

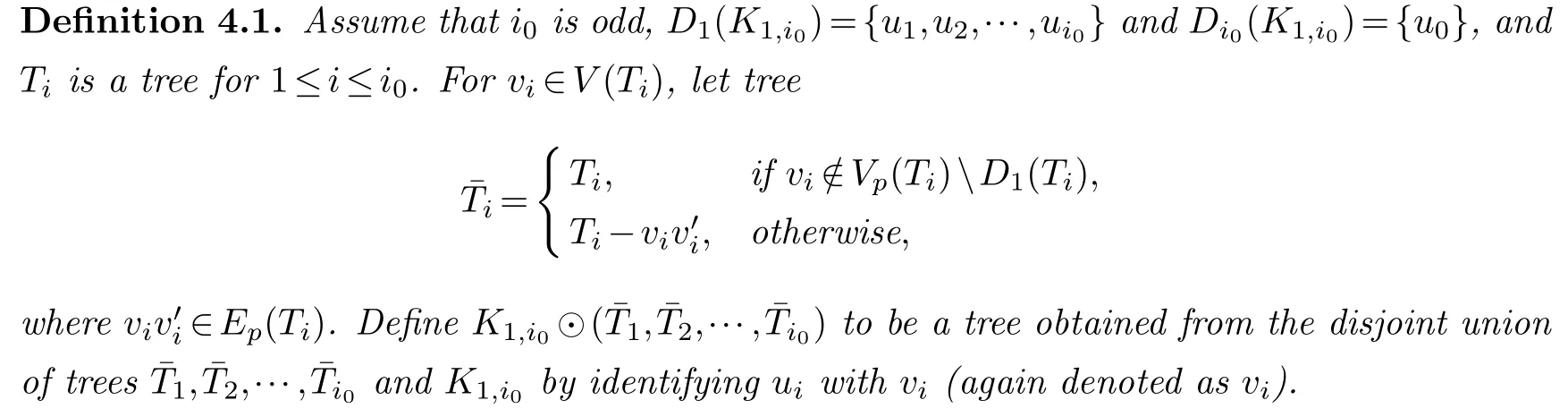
Lemma 4.1.If Ti is(k-1)-cutwidth critical for1≤i≤3,then c(K1,3⊙(T1,T2,T3))k.

Proof.With notation in Definition 4.1,letTK1,3⊙(T1,T2,T3).IfdT(vi)2 (i1,2,3),then the series reduction can be implemented without effecting onc(T)k.For 1≤i≤3,u0viis a pendant edge of subgraphTi+u0viinTclearly.SinceT2is (k-1)-cutwidth critical,c(T2+u0v2)c(T2)k-1 by Lemma 2.2.There are two cases to consider: (1)vi D1(Ti);(2)vi/D1(Ti).

Subcase 1.vi D1(Ti)for 1≤i≤3.In this case,dT(vi)2,K1,3⊙(T1,T2,T3)T(u0;T1,T2,T3)after the series reduction is implemented.By Lemma 2.1(iii),c(T)k.

Subcase 2.vi D1(Ti)fori1,3 butv21(T2).From the structure ofT,T-{u0v1,u0v3}has three componentsT1-u0v1,T2+u0v2,T3-u0v3,andc(T1-u0v1)≤k-2,c(T3-u0v3)≤k-2 by the criticality ofT1andT3.Suppose that the optimal labelings ofT1-u0v1,T2+u0v2,T3-u0v3aref1,f2,f3respectively,then definef:V(T)→S|V(T)|to be labeling by the order (f1,f2,f3).By (1.3),eachf-max-cut ofTmust be anfi-max-cut ofTiplus the newly added edgeu0v1oru0v3,and soc(T,f)≤(k-1)+1kwhich impliesc(T)≤k.On the other hand,c(T)≥kby Lemma 2.1(ii),this is because the vertexu0satisfiesc(T(u0;vi,vj))k-1 for any verticesvi,vj NT(u0) inT.Thusc(T)k.

Subcase 3.v11(T1) butvi/D1(Ti) fori2,3.From the structure ofT,T-{u0v1,u0v3}has three componentsT1-u0v1,T2+u0v2andT3withc(T1-u0v1)≤k-2,c(T2+u0v2)k-1,c(T3)k-1.So,similar to that of Subcase 2,c(T)k.

Subcase 4.vi/D1(Ti) for 1≤i≤3.SinceT-{u0v1,u0v3}has three componentsT1,T2+u0v2andT3,similar to that of Subcase 3,c(T)k.The proof is completed.

By Definition 4.1,in case (1)

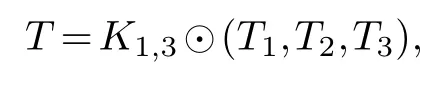
in case (2)

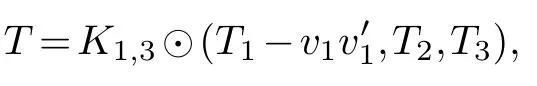
in case (3)

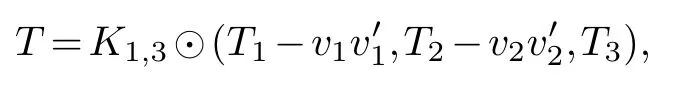
and in case (4)

For case(1),letdT(v)/2 for(T),since a series reduction can be first carried out,otherwise.From the structure ofT,T1,T2andT3are three components ofT-u0.Without loss of generality,letvv′Ep(T2).Then,by assumption,c(T1)k-1,c(T2-vv′)k-2 andc(T3)k-1 with optimal labelingsf1,f2,f2respectively.Thus,define a labelingf:V(T)→{1,2,···,|V(T-v′)|}ofT-vv′by the order(f1,f2,f3).Asu0v1,u0v3are both cut edges inT-vv′,c(T-vv′,f)≤k-1,which impliesc(T-vv′)≤k-1.Sou0is ak-critical vertex ofT.ThusTisk-cutwidth critical by Theorem 2.1.Likewise,in cases (2)-(4),u0is a strongk-critical vertex ofTresulting in thatTisk-cutwidth critical also.

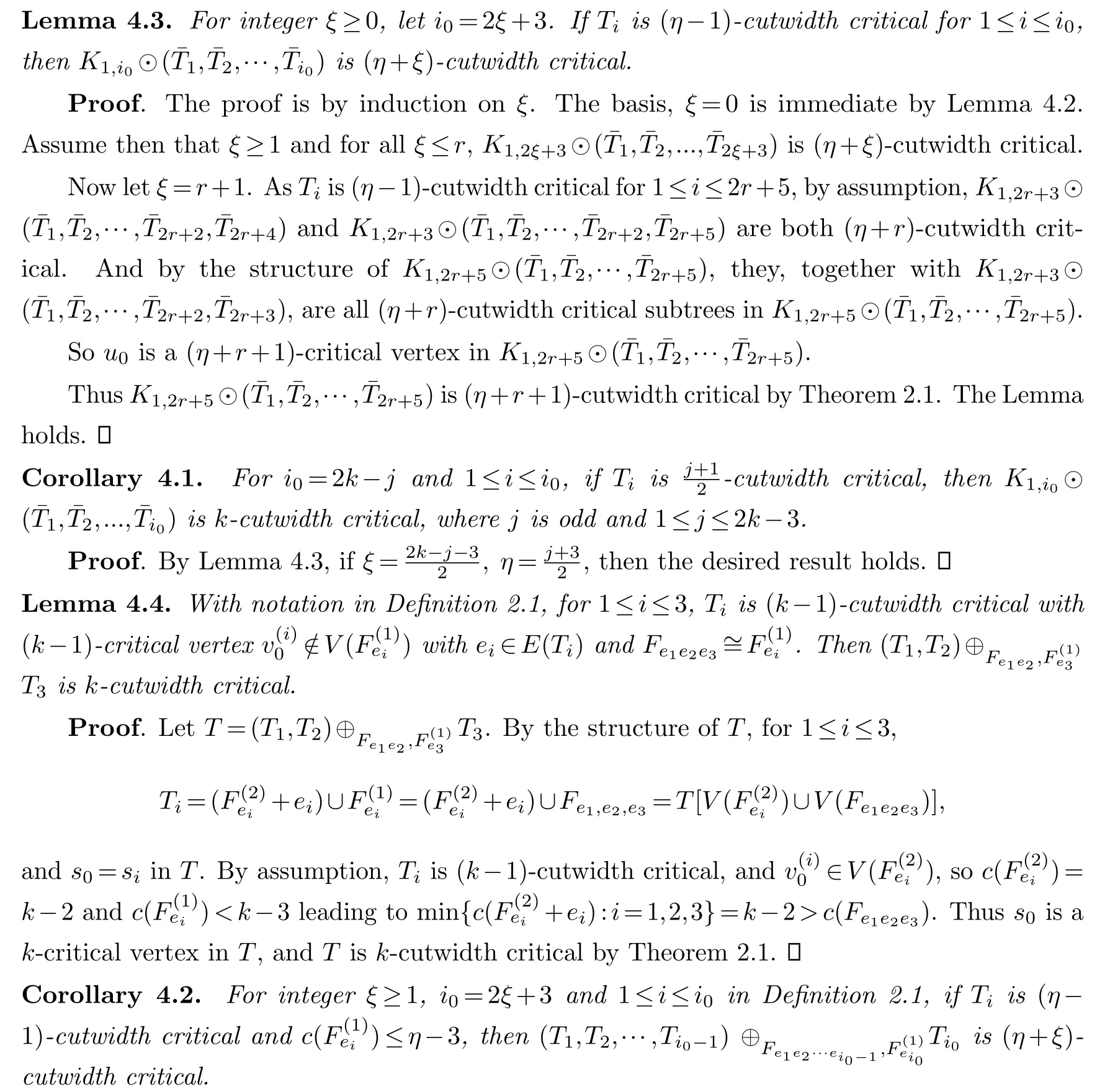
Proof.Similar to that of Lemma 4.3,the proof can be done by induction onξ,omitted here.

Likewise,with an argument similar to Lemma 4.4,we have

Definition 4.2.With notations in Definitions 2.1-2.2,for1≤i,j ≤3,define

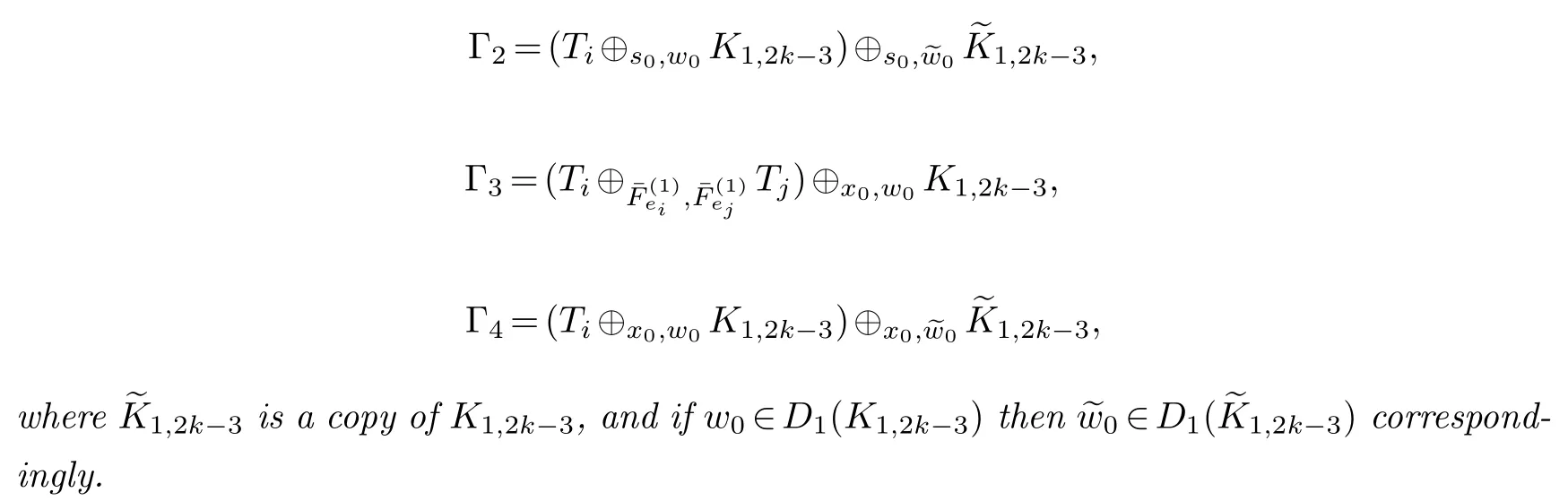
Lemma 4.6.For1≤i,j ≤3,if Ti,Tj are(k-1)-cutwidth critical,then each of {Γi:1≤i≤4}is k-cutwidth critical.

Proof.Similar to that of Lemma 4.4,omitted here.

In Definition 2.1,for 1≤i≤i0withi0＞3,letc(Ti)η,≤η-2,

Definition 4.3.With notations in Definitions 2.1-2.2,for i0＞3,define

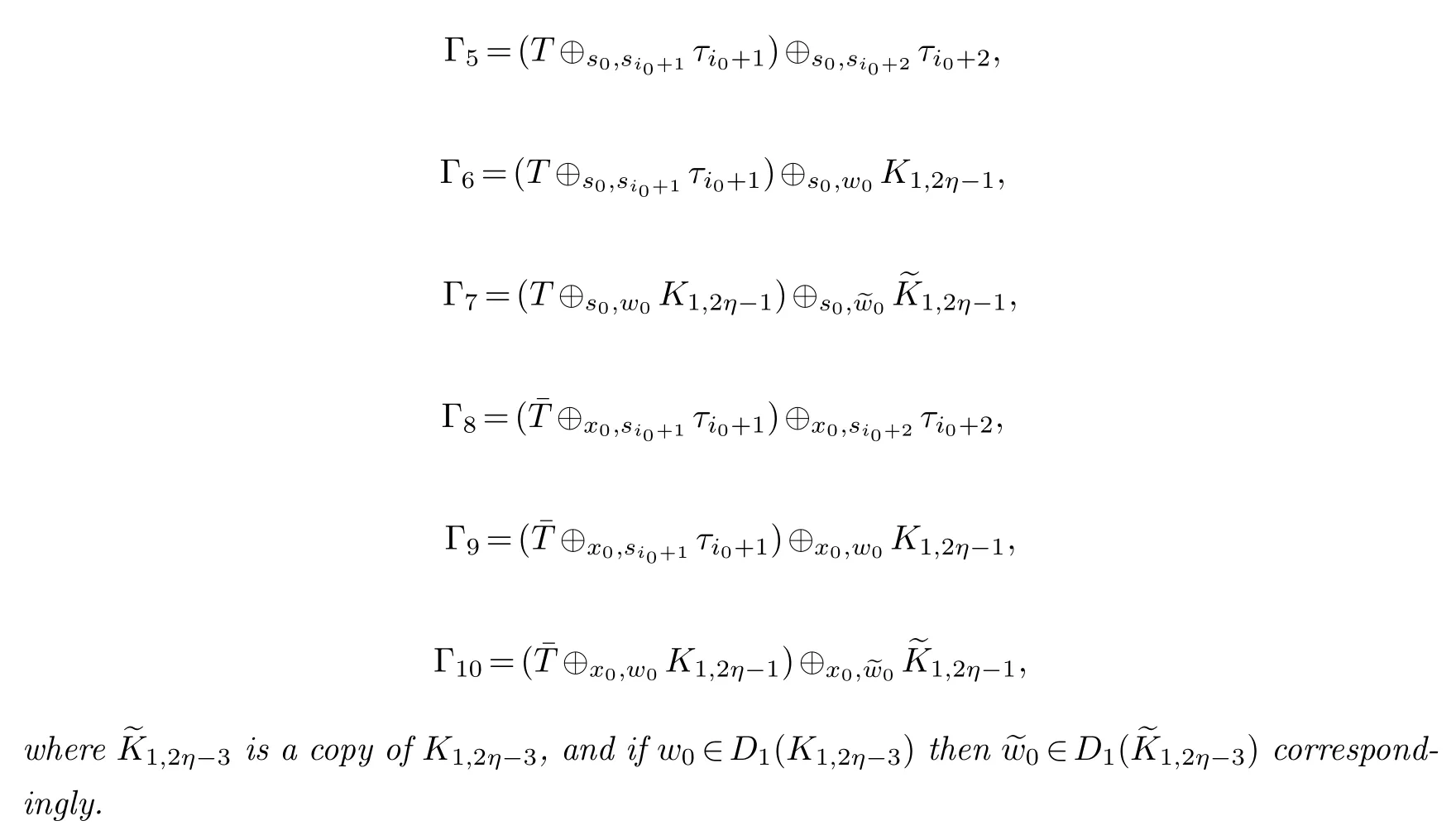
In Lemmas above,we showed that

and Γ1-Γ10arek-cutwidth critical,which are formed by Definitions 2.1,2.2,4.1-4.3 respectively.For convenience,in the following,we shall simply say that the constructional methods given by Definitions 2.1,2.2,4.1-4.3 are Method 1,Method 2,···,Method 5,respectively.

Theorem 4.1.A tree T is k-cutwidth critical if and on if T can be formed by one of Methods 1-5.

Proof.Sufficiency.The result is obvious by Lemmas 4.2-4.7.

Necessity.By assumption,Tisk-cutwidth critical,soThas either ak-critical vertex or a strongk-critical vertexv0by Theorem 2.2.Thus two cases are needed to consider as follows.

§5.Concluding remark

The paper investigates the methods of forming ak-cutwidth critical treeT.As an additional result,an efficient method of finding an optimal labelingf*ofTis also obtained.Some special methods of forming a specific nontree critical graphGhave been gotten.For example,a graphG,which is obtained by identifying1(H1)1(H3) and1(H4),is 4-cutwidth critical.But the general methods of constructing nontree critical graphs have not been known.This is a task to study in the future works.

Acknowledgement

Mr.Zhang Zhenkun is Mr.Lin Yixun’s doctor (2003).This article is to celebrate Mr.Lin’s 85th birthday.