Induced Matching-Extendability of Halin Graphs

HUI Zhi-hao YANG YuWANG An

(1.School of Mathematics and Statistics,Pingdingshan University,Pingdingshan 467000,China;2.International Joint Laboratory for Multidimensional Topology and Carcinogenic Characteristics Analysis of Atmospheric Particulate Matter PM2.5,Pingdingshan 467000,China;3.School of Software,Pingdingshan University,Pingdingshan 467000,China)

Abstract: Let G be a connected graph having a perfect matching.The graph G is said to be induced matching (IM) extendable if every induced matching M of G is contained in a perfect matching of G.In this paper,we show that Halin graph GT ∪C is IMextendable if and only if its characteristic tree T is isomorphic to K1,3, K1,5, K1,7 or S2,2.

Keywords: Halin graph;Perfect matching;Induced matching;Induced matching extendable

§1.Introduction

All the graphs considered in this article are finite simple and connected.LetGbe a graph with vertex set and edge set denoted byV(G) andE(G) respectively.For a vertex,NG(v)denote the set of neighbors ofvinGand letdG(v)|NG(v)|denote the degree of a vertex(G).The distance between two vertices(G) is the length of the shortest path joining them.We denote byd(G) the diameter of a graphGand is defined as the maximum distance over all pairs of vertices ofG.The girth of a graphG,denoted byg(G),is the length of the shortest cycle ofG.LetKm,nandSp,q(in Figure 1) denote the complete bipartite graph and the double-star graph,respectively.A Halin graph is a planar graphGT ∪C,whereTis a tree on at least four vertices with no two vertices having degree two,andCis a cycle connecting the leaves ofTin the cyclic order determined by the embedding ofT[4].Tis called the characteristic tree ofGand the cycleCis called the characteristic cycle ofG(see Figure 2).For the terminologies and notations not defined in this paper,we refer the readers to [1].

The matching theory is one of the core contents of graph theory.The matching extendability is a significant topic in matching theory.Plummer [10] first proposed the notion ofn-extendability: A graphG(|V(G)|≥2n+2) is said to ben-extendable if every matchingMwithnedges can be extended to a perfect matching ofG.The latest results onn-extendability can be found in [6] and [5].An induced matchingMin the graphGis a matching such that no two edges ofMare joined by an edge ofG[2].In other words,an induced matching is a matching that forms an induced subgraph (G[V(M)]M).In 1998,Yuan proposed the concept of induced matching (IM) extendable graph [16]: A graphGis said to be induced matching extendable if every induced matchingMofGis included in a perfect matching ofG.In 2007,Wang et al.[13] suggested a variant of then-extendability:Gis bipartite-matching (BM)extendable if every bipartite matchingMofGis included in a perfect matching ofG.Many celebrated results on matching extendability can be found in [7–9,11,17,18].

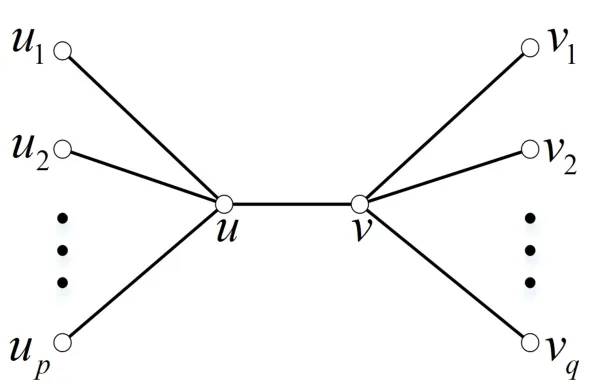
Fig.1 Double-star graph.

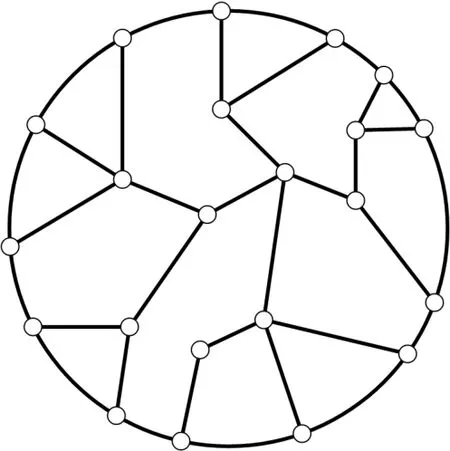
Fig.2 Halin graph.

§2.Preliminaries

There are many known results about induced matching extendable graphs.The following is a part of the list.

Lemma 2.1.[12] (Tutte’s Theorem) A graph G has perfect matchings if and only if for every S ⊆V(G),o(G-S)≤|S|.Here,o(G)is the number of odd components of graph G.

Lemma 2.2.[3] A bipartite graph G[X,Y]has a perfect matching if and only if |X||Y| and|N(S)|≥|S| for all S ⊆X.

Lemma 2.3.[16] If G is a connected IM-extendable graph with |V(G)|≥4,then |V(G)| is even and G is2-connected.

If 1≤m≤n,then everyn-extendable graph ism-extendable.We have the following results.

Lemma 2.4.[16] If G is an n-extendable graph and G has no induced matching M with|M|＞n,then G is an induced matching extendable graph.

Lemma 2.5.[16] For a connected induced matching extendable graph G,if |V(G)|≥4,then g(G)≤4.

Lemma 2.6.[16] A graph G is induced matching extendable if and only if for every induced matching M of G and every S ⊆V(G)/V(M),o(G-V(M)-S)≤|S|.

Lemma 2.7.[14] Let e and f be two nonadjacent edges of a graph G.If G-e and G-f are both induced matching extendable,then G is also induced matching extendable.

Lemma 2.8.[15] The induced matching problem is NP-complete for Claw-free graphs.

Lemma 2.9.[15] The induced matching extendable problem is co-NP-complete for graphs with diameter 2 and bipartite graphs with diameter 3.

The problem of the extendability of induced matching has been a theoretical study in which many graph theorists have indulged.In 2000,Yang and Yuan [15] proposed that the induced matching problem is NP-complete and the induced matching extendable problem is co-NP-complete.

Motivated by these scholars’ theories,in this paper we characterize the induced matching extendability of the Halin graph.The main result is as follows: Halin graphGT ∪Cis induced matching extendable if and only if its characteristic treeTis isomorphic toK1,3,K1,5,K1,7orS2,2.

§3.The main results

Theorem 3.1.Halin graph GK1,2n-1∪C is IM-extendable if and only if n2,3,4.

Proof.Letn≥2 andV(G){u,v1,v2,···,v2n-1}denotes the vertex set of Halin graphGK1,2n-1∪C.Suppose the degree sequence of its characteristic treeTis{2n-1,1,1,···,1}.According to the topology of the graphGcorresponding to the characteristic treeT,we have the following assertions: for every induced matchingMofG,if|M|≥2,then(M).Disproof:if(M) and|M|≥2,then there must beG[V(M)]/MinG.This contradicts the fact that the matchingMis the induced matching ofG.In the following,we consider the order of the Halin graph.

Case 1.n2

LetMbe any induced matching of the Halin graphGK1,3∪C.By assertion and|C|3,we get|M|1.ThenG-V(M) is isomorphic toK2which has a perfect matching.ThereforeGis IM-extendable.

Case 2.n3

From the assertion,if|M|≥2,then(M).Hence,only induced matchingMcan be selected from characteristic cycleC.Since|C|5,we get|M|1.ThenG-V(M)is isomorphic toK4-eorP4.Both the graphsK4-eandP4have a perfect matching.ThereforeGK1,5∪Cis IM-extendable.

Case 3.n4

LetMbe any induced matching ofGK1,7∪C.According to the assertion and|C|7,we get|M|1,2.

·Let|M|1,thenG-V(M) is isomorphic toF5orP6.Both the graphsF5andP6have a perfect matching.Therefore,GK1,7∪Cis IM-extendable.

·Let|M|2,then(M).In other wordsE(M)⊂E(C).Without loss of generality we can take the induced matchingM{v1v2,v4v5},namelyG[{v1,v2,v4,v5}]M.ThenG-V(M)is isomorphic toK1,3+ethat has a perfect matching.Therefore,GK1,7∪Cis IM-extendable.

Case 4.n≥5

Letn≥5 and consider an induced matchingM{v1v2,v4v5,v7v8}selected fromGK1,2n-1∪C,namelyG[{v1,v2,v4,v5,v7,v8}]M.It can be seen thatG-V(M)has two pendant edges{uv3}and{uv6}.Hence there is no perfect matching.

Therefore,Gis not IM-extendable.

Theorem 3.2.Let p≥2,q ≥2,p+q2k and GSp,q ∪C be a Halin graph.Then G is IM-extendable if and only if p2,q2.

Proof.LetSp,q(see Figure 1) be a double-star graph withnp+q+2 vertices.Supposeuandvare two centers and|N(u)/v|p,|N(v)/u|q.

Letp2,q2,then the induced matchingMofGS2,2∪Chas|M|1.Otherwise,there must beG[V(M)]/Min the induced matchingM,a contradiction.ThenG-V(M)is isomorphic toK1,3+eorC4.Both the graphsK1,3+eandC4have a perfect matching.Therefore,Gis IM-extendable.

Letp＞2 orq ＞2 (p+q2k).Consider an induced matchingM{u1u2,vv2}selected fromGSp,q ∪C,namelyG[{u1,u2,v,v2}]M.Sinced(v1)3 and the three edges associated with{v1}are associated with the vertices of the induced matchingM,that isV(M){u1,u2,v,v2}.Therefore,there must have an independent component{v1}ofV(G)-V(M) so that it cannot form a perfect matching ofG.Therefore,Gis not IM-extendable.

Theorem 3.3.Let |G|≥8and GT ∪C be the Halin graph.If d(G)≥4,the number of vertices of degree one in the characteristic tree T corresponding to G is at least 5.

Proof.Letsbe the number of vertices of degree one in the characteristic treeTcorresponding toG.From the degree sum formula and the definition of Halin graph,we get

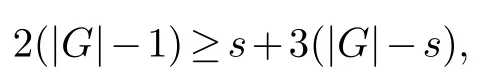
then

Theorem 3.4.Halin graph GT ∪C is IM-extendable if and only if its characteristic T is isomorphic to K1,3,K1,5,K1,7or S2,2.

Proof.In the following four cases,the diameter of the Halin graph is discussed.

Case 1.Letd(G)1,then its characteristic treeTis isomorphic to the null graph.

Case 2.Letd(G)2,then its characteristic treeTis isomorphic toK1,2n-1.By Theorem 3.1,Halin graphGK1,2n-1∪Cis IM-extendable if and only ifn2,3,4.

Case 3.Letd(G)3,then its characteristic treeTis isomorphic toSp,q(p≥2,q ≥2).By Theorem 3.2,Halin graphGSp,q ∪Cis IM-extendable if and only ifpq2.

Case 4.Letd(G)≥4 andP{u0u1u2···ud}be the longest path inG.By definition of the Halin graph no two vertices of the characteristic treeThave degree two,it follows thatu1orud-1must be adjacent to at least two leavesT.From Theorem 3.3,the order of cycleCformed by joining all the pendant vertices ofTis at least 5.LetC{v1v2···vsv1}withs≥5 and{u0}{v1}.Supposeu1orud-1be adjacent to at least two leaves ofT,that isu1andv1,v2,···,vt(s＞t≥2) are adjacent.Thenu1,vt+1andvt+2are not adjacent.Hence{u1,vt+1}and{vt,vt+2}are independent set.Now,the matchingM{u1vt-1,vt+1vt+2}is an induced matching.Sincevtis the leaf vertex of characteristic treeT,henced(vt)3.Also,the vertexvtis adjacent tou1,vt-1,vt+1,it follows thatV(G)-V(M) has at least one pendant vertexvt.Therefore there is no perfect matching.

§4.Concluding remarks

In this paper,the induced matching-extendability of Halin graphs is explored.In the process of exploration,according to the structure of characteristic tree,Halin graph is divided into three categories.We draw the following conclusions: Halin graphGT ∪Cis IM-extendable if and only if its characteristic treeTis isomorphic toK1,3,K1,5,K1,7andS2,2.

The induced matching extendable graph must be a 1-extendable graph,so the induced matching extendability of a graph can be regarded as a deformation of then-extendable problem.Huang and Shi in [5] give short inductive proofs of two known results onk-extendible graphs based on a property proved.Everyk-extendible graph is (k+1)-connected;letG(X,Y) be a connected bipartite graph with a perfect matching and|G|≥2k+2.ThenGisk-extendible if and only if|N(A)|≥|A|+kfor every subsetA⊆Xwith 1≤|A|≤|X|-k.In the follow-up research,we will focus on thek-extendability of Halin graph.

Acknowledgment

The authors would like to thank referees for providing valuable suggestions,which greatly improved the paper.