一种G2连续组合曲线的表示

严兰兰， 宋希辰， 魏子华， 谢 磊

一种2连续组合曲线的表示

严兰兰， 宋希辰， 魏子华， 谢 磊

(东华理工大学理学院，江西 南昌 330013)

针对Bézier曲线以及现有众多含形状参数的扩展Bézier曲线的2拼接条件均对控制顶点有严格要求的问题，拟提出一种2连续组合曲线，其能综合Bézier与B样条方法的优点，其基函数具有显式表达式，既具有B样条方法的自动光滑性，又能轻松拥有Bézier曲线的端点几何特征。为此，构造了一组含6个参数的基函数，按照3次Bézier曲线的定义方式由之构造了基于4个控制顶点的曲线段，根据曲线段的拼接条件，按照3次B样条曲线的定义方式构造了基于4点分段的组合曲线。基函数具有全正性，其同时包含3次Bernstein基函数和所有由内部节点重复度均为1的节点向量所确定的3次B样条基函数作为特例。曲线段具有保凸性、端点位置以及形状可调性，其同时包含3次Bézier曲线和3次B样条曲线段作为特例。组合曲线的定义方式自动保证了其整体2连续，将部分参数取特定值，即可使其端点插值、端边相切，此时其中依然存在用于调整内部形状的独立参数。按一定规则选取组合曲线中的参数，即可重构2连续的3次B样条曲线。

曲线设计；B样条方法；Bézier方法；几何连续；形状参数

Bézier方法与B样条方法是几何设计中描述自由型曲线曲面的基本方法，二者各具优点，但也存在一个共同的不足，即在一定条件下不具备形状可调性。具体地，Bézier方法采用Bernstein多项式作为基函数，控制顶点的数量决定其所需基函数的次数，而次数一旦指定，基函数便完全确定。B样条方法采用B样条作为基函数，指定其次数，再给定节点向量(其所含节点数量与基函数次数有关)，B样条基函数便随之确定。因此，对于Bézier方法而言，一旦控制顶点给定，Bézier曲线曲面的形状便被唯一确定；对于B样条方法而言，若控制顶点和节点向量均给定，则B样条曲线曲面的形状也被唯一确定。正因为如此，文献[1-14]均以增加形状调整自由度为主要目标展开了对Bézier或B样条方法的扩展研究，大量含形状参数的扩展Bézier或扩展B样条曲线曲面应运而生。上述文献的共同之处在于构造了含自由参数的基函数，且具有类似于Bernstein基函数[1-7]或B样条基函数[8-14]的诸多性质，由其定义的曲线曲面分别具有类似于Bézier或B样条曲线曲面的众多性质，同时还拥有Bézier与B样条方法不具备的形状可调性，即可以通过改变基函数中的自由参数来调整曲线曲面的形状。虽然文献[15-18]的主要研究目标有别于上述文献，但其中给出的曲线曲面模型同样具有独立于控制顶点和节点向量的形状调整自由度。

注意到在曲线设计中，对于开曲线而言，通常希望其具有Bézier曲线的端点几何特征。即：曲线首末端点为控制多边形的首末顶点，曲线在端点处与控制多边形相切。若直接采用Bézier方法进行曲线设计，该特征自动满足，但单一的Bézier曲线段难以描述复杂形状，组合Bézier曲线具有描述复杂形状的潜能，但为了保证组合曲线在连接处的光滑性，相邻曲线段的控制顶点之间需满足严格的约束关系。相比而言，B样条曲线在连接处的光滑性由B样条基函数在相应节点处的连续性自动保证。鉴于此，采用B样条方法描述复杂形状更加方便。为了使B样条曲线具有Bézier曲线的端点几何特征，需将两端的节点重复度取为+1 (为曲线次数)，而内部节点，只要在数学上成立即可。但无论内部节点是否均匀，此时的B样条基函数都属于非均匀型，因此在定义域内各节点区间上，即使采用局部参数表示，其基函数也不会具有像均匀B样条基函数那样统一的显式表达式。因此，要获取基函数表达式，只能由具体的节点向量通过递推公式进行递推计算。概括而言，Bézier曲线具有良好的端点几何特征，Bernstein基函数具有统一的显式表达式，2个优点都是B样条曲线不具备的，但B样条曲线胜在自动光滑。

虽然现有文献给出了各种扩展的Bézier曲线或扩展的B样条曲线，但目前没有哪种扩展方法能集Bézier与B样条方法的优点于一身。大部分扩展Bézier曲线的拼接条件与Bézier曲线类似，因此在描述复杂形状时并不方便，虽然文献[19]给出了易拼接的扩展Bézier曲线，但其在端点处的曲率为零。虽然文献[10-14,17-18]给出的扩展B样条基函数具有显式表达式，但其无法自动具备Bézier曲线的端点几何特征。

基于上述分析，同时考虑到2连续可以满足工程中大部分设计需求，因此本研究希望给出一种新的曲线表示方法，使其既具有显式表达的基函数，又能自动实现2连续，同时还可以轻松拥有Bézier曲线的端点几何特征。

1 基函数及其性质

1.1 基函数的表示

3次Bernstein基函数给出一组新的基函数。

其中，

1.2 基函数的性质

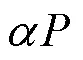
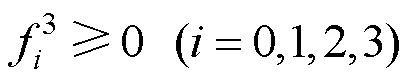
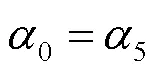
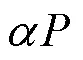
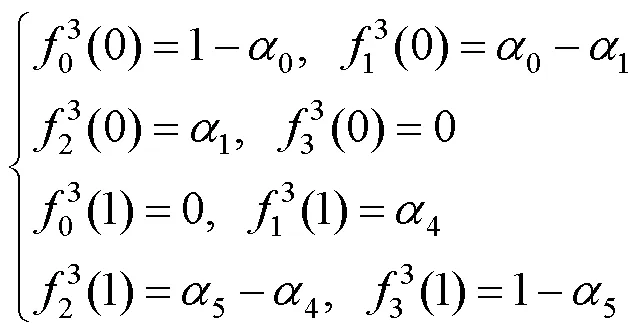
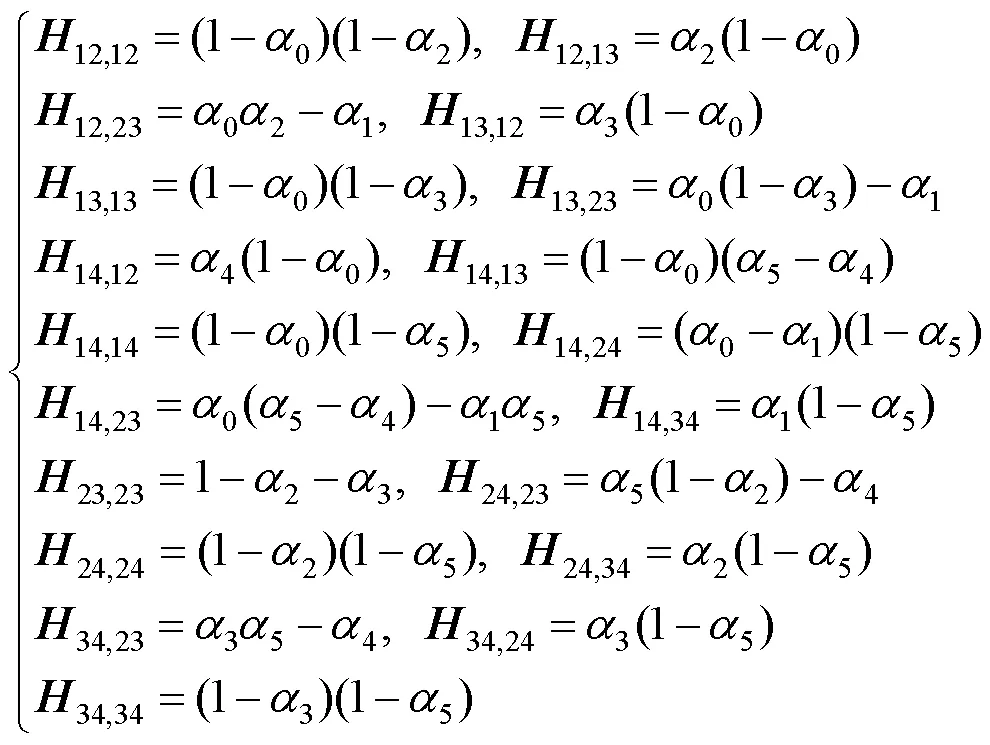
其余全为0，其中，,kl为的与行，与列形成的子式；的16个3阶子式为

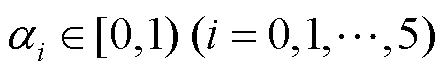
2 曲线及其性质

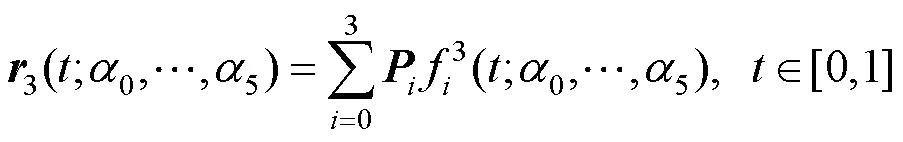
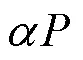
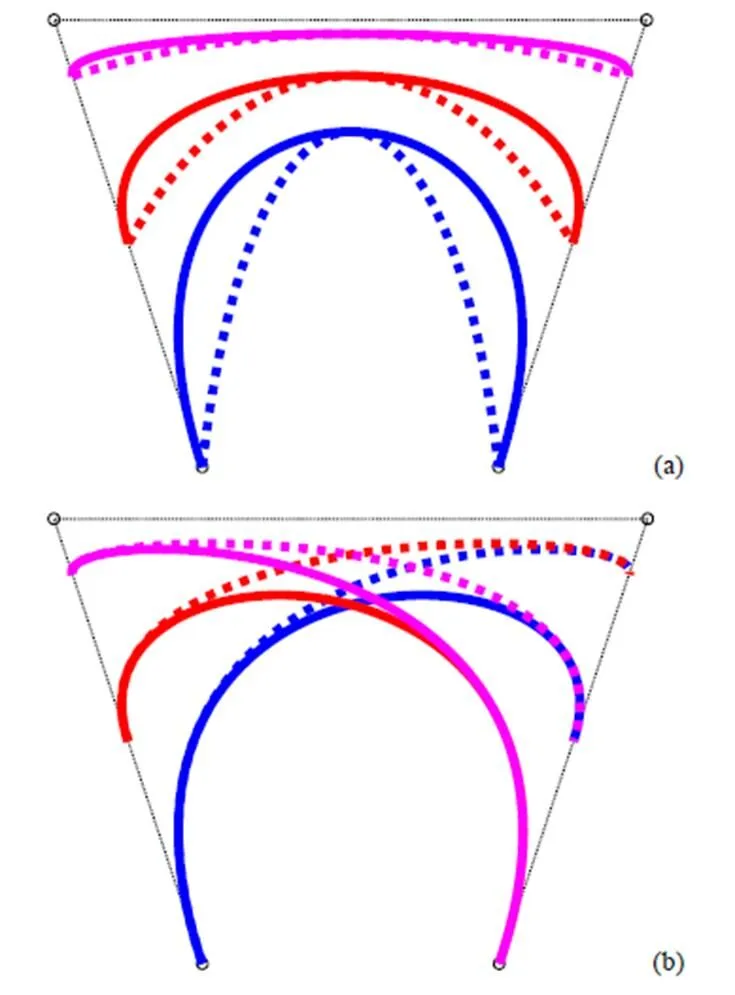
图1 端点在端边上的3次aP曲线((a)对称；(b)非对称)

图2 端点不在端边上的3次aP曲线((a)对称；(b)非对称)

3 曲线拼接条件

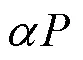
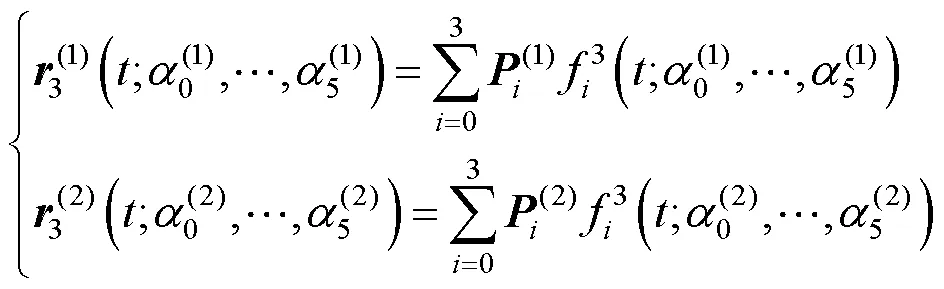
由式(4)和式(5)可得

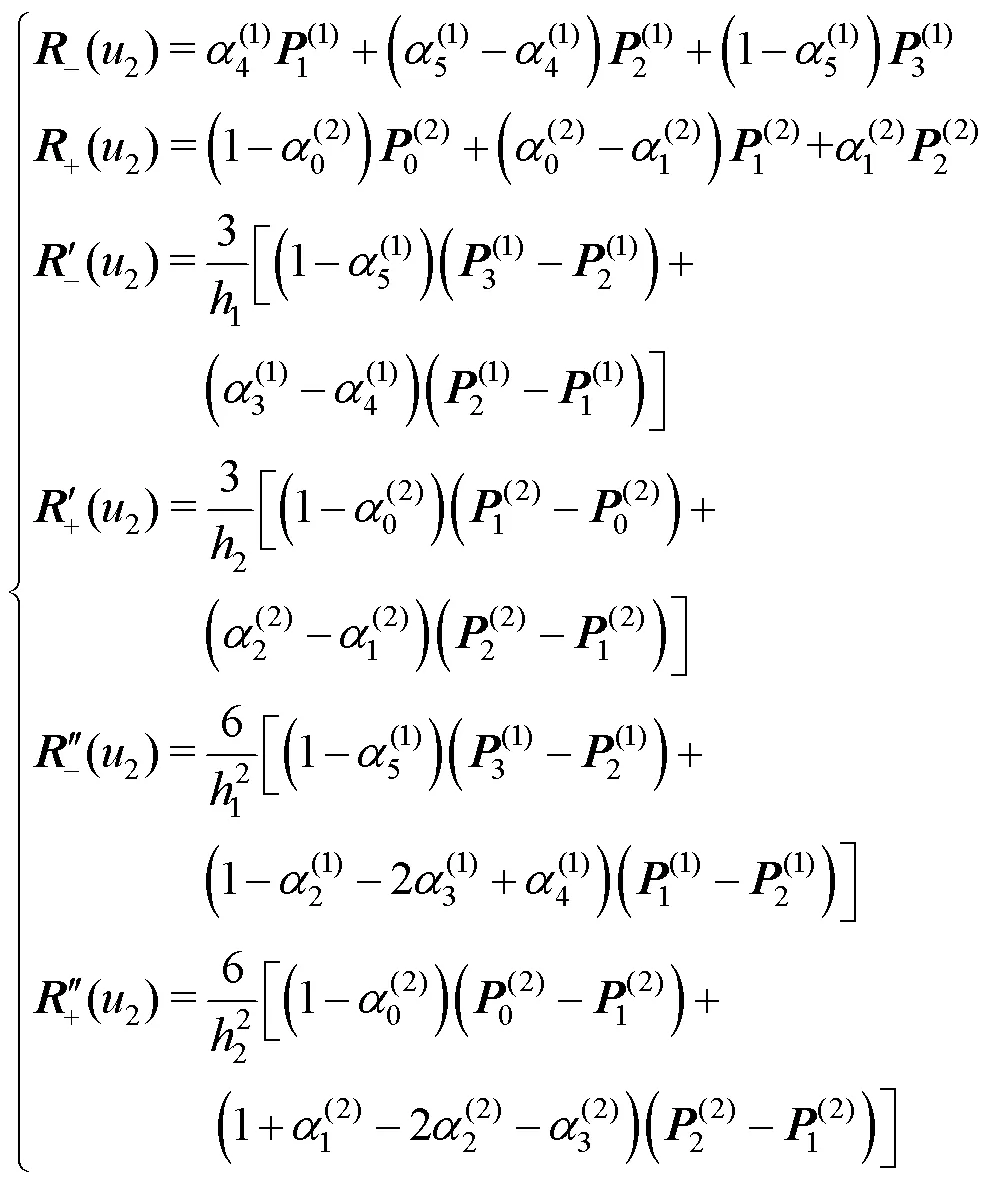
若

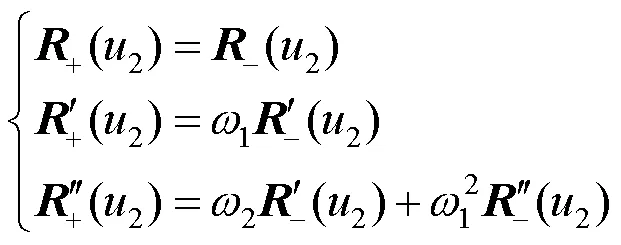
其中，

说明曲线()在节点2处2连续。

4 组合曲线的定义

根据拼接条件(7)，接下来定义一种在分段连接点处能自动满足2连续性的组合曲线。

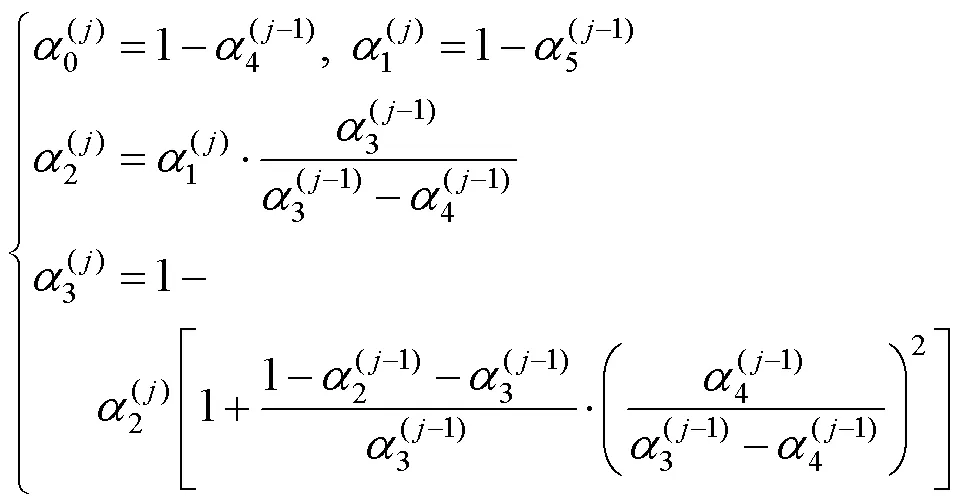
注7：在实际的组合曲线设计中，如果并不要求所有的连接处都2连续，例如某些指定的曲线段之间只需满足1或0连续，则只需让指定曲线段的参数之间仅满足式(9)中前2行或第1行的关系即可。

5 组合曲线参数的选取

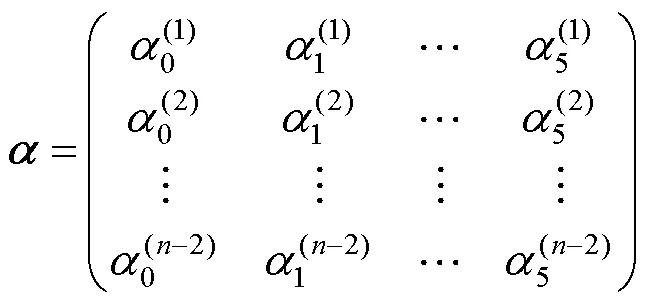
这些条件可以转化为更易于使用的等价形式

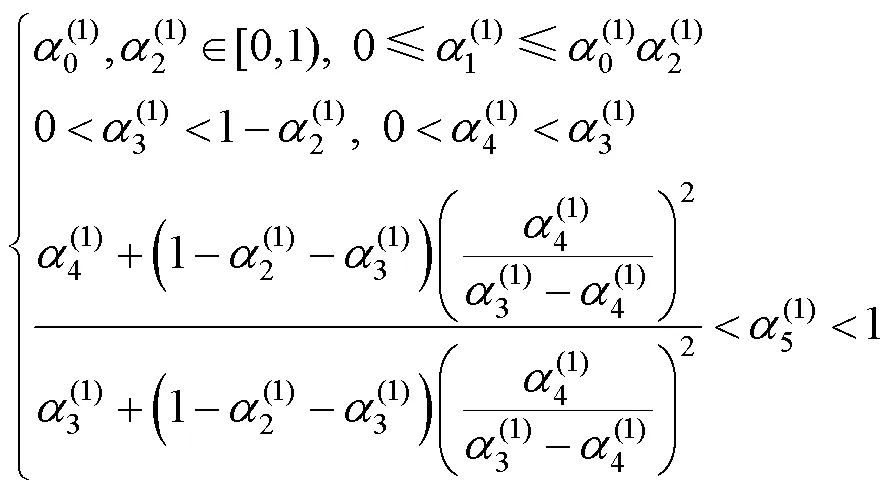
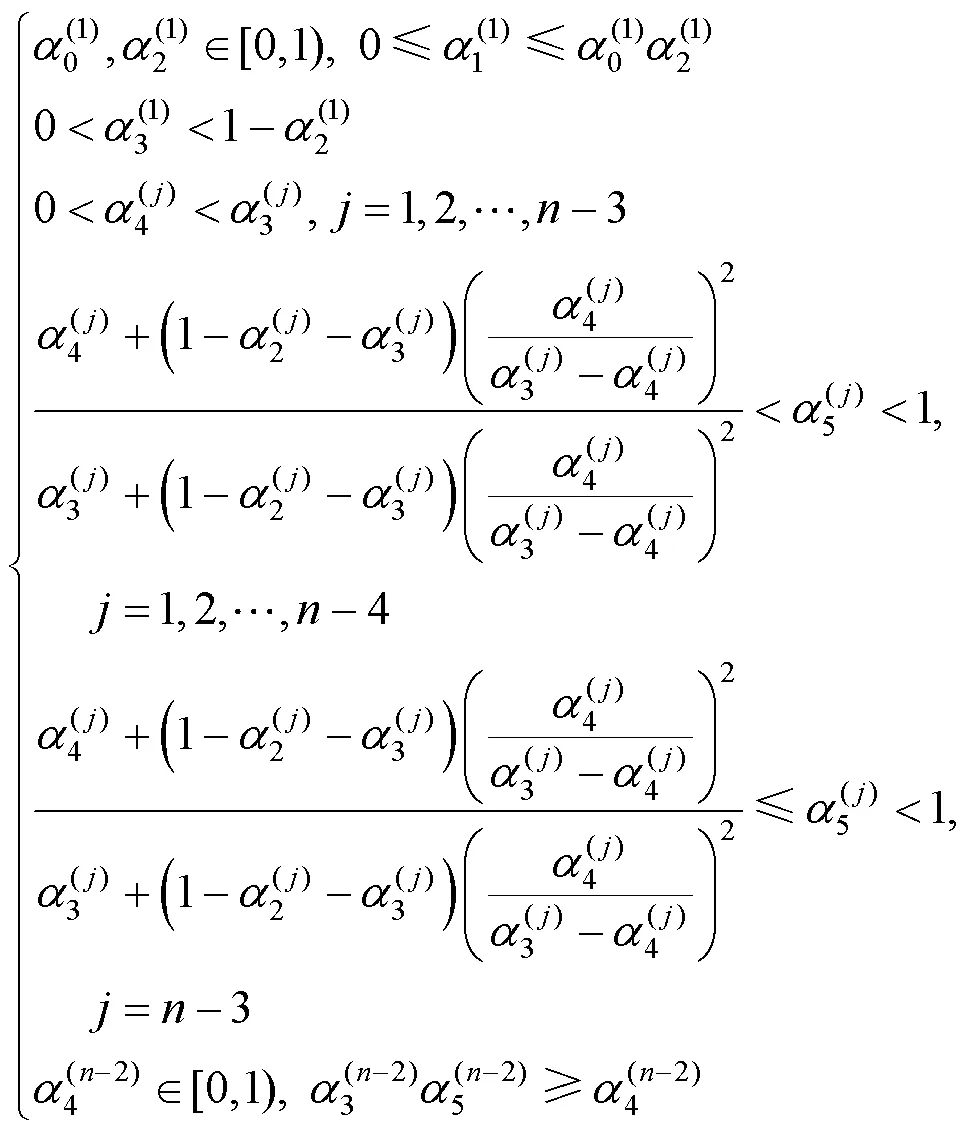
(1) 根据约束条件(11)选取第1段的参数。

(2) 由第1段的参数，根据式(9)通过计算确定第2段的前4个参数，根据约束条件式(11)选取第2段的后2个参数。

6 B样条曲线的重构

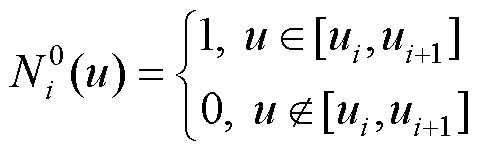
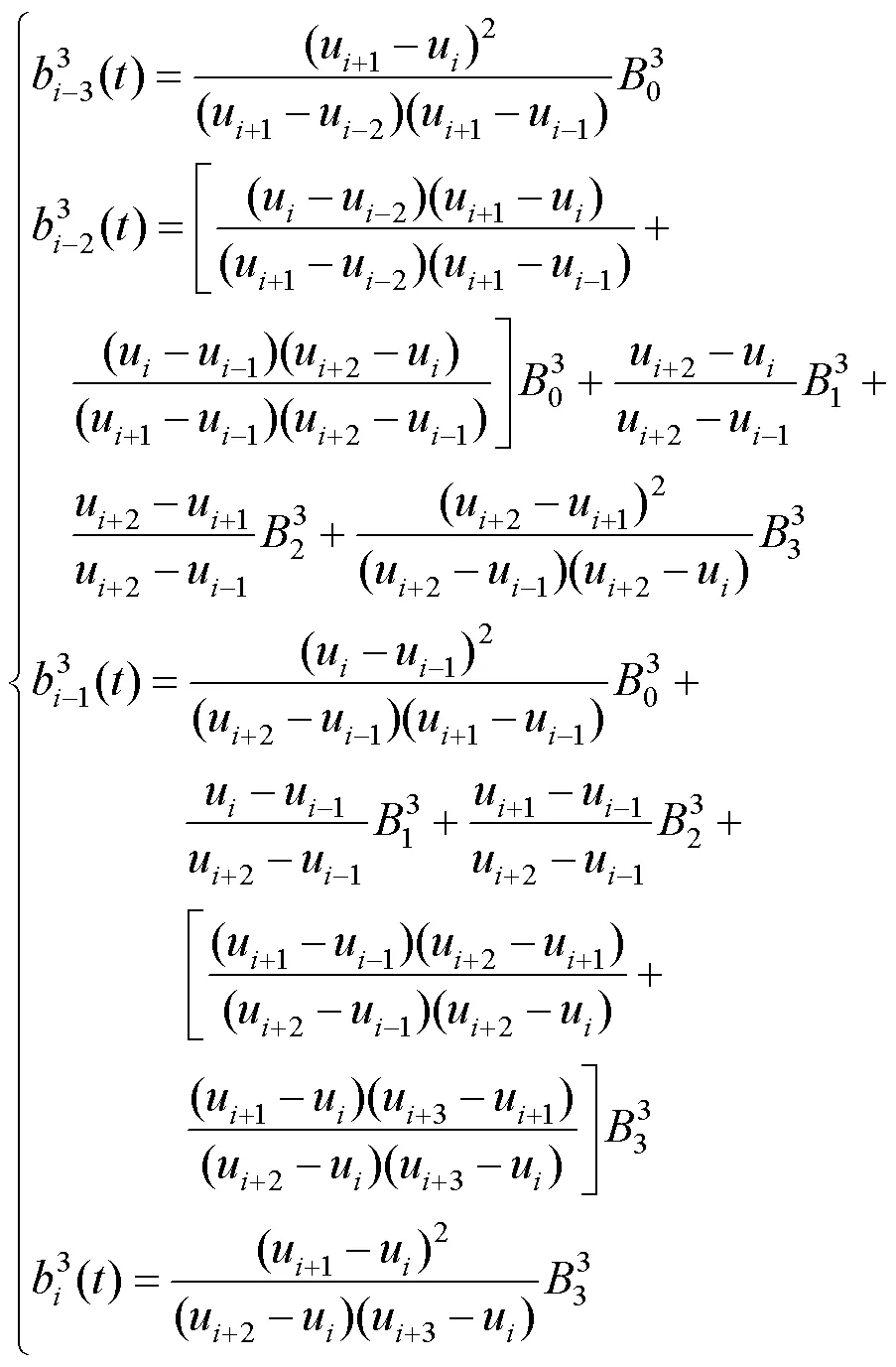
将3次B样条曲线的方程从整体表示改写成分段表示后，每一段上的基函数即由式(12)给出。

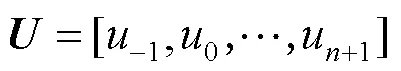
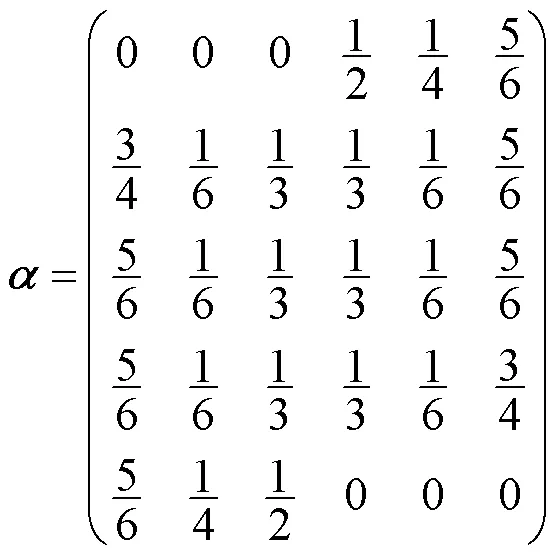
与上述情形对应的曲线即为由相应控制顶点定义的3次准均匀B样条曲线。

7 组合曲线图例

图3 C2连续组合3次aP曲线((a)均匀；(b)准均匀； (c)非均匀)

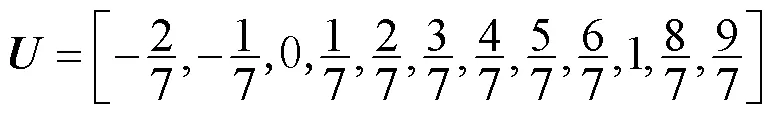
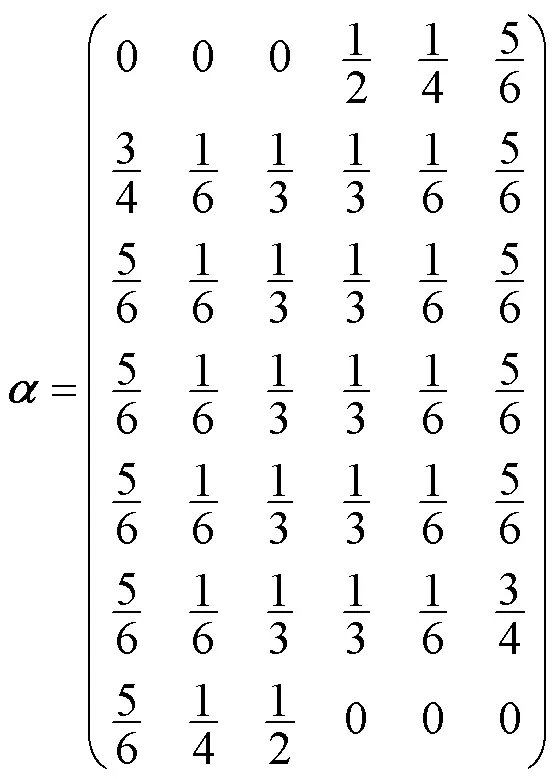
按照第5节所述流程，获取如下3组参数

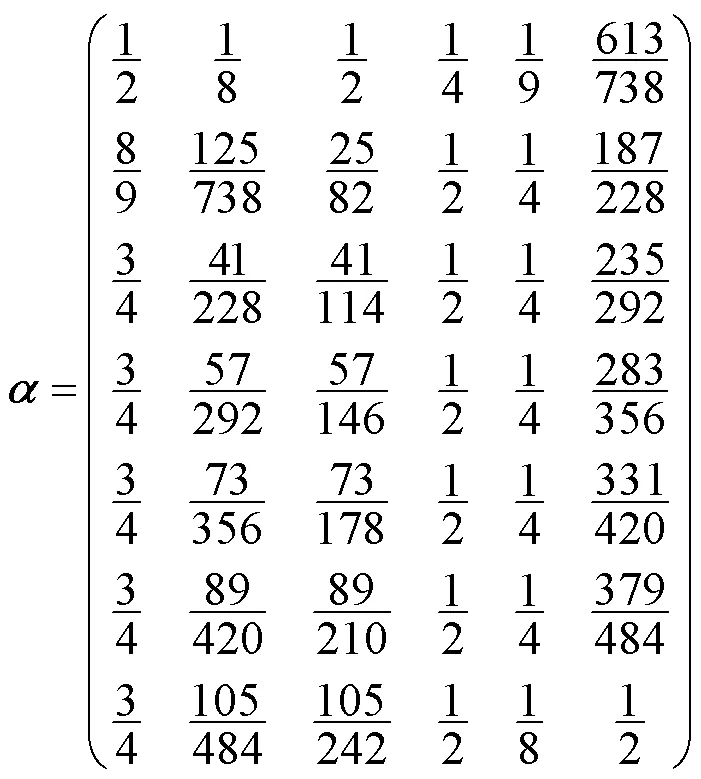
图5(a)中第3段与第4段之间0连续，其余段之间2连续。图5(b)中第2段与第3段之间0连续，其余段之间2连续。

图5 数字设计((a)数字2；(b)数字3)

8 总 结

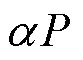
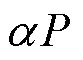
下一步的研究计划是构造基于(≥5)点分段的G(2≤≤-2)连续组合曲线，并对相应的组合曲面展开分析。

[1] 吴晓勤, 韩旭里. 三次Bézier曲线的扩展[J]. 工程图学学报, 2005, 26(6): 98-102.

WU X Q, HAN X L. Extension of cubic Bézier curve[J]. Journal of Engineering Graphics, 2005, 26(6): 98-102 (in Chinese).

[2] YAN L L, LIANG J F. An extension of the Bézier model[J]. Applied Mathematics and Computation, 2011, 218(6): 2863-2879.

[3] QIN X Q, HU G, ZHANG N J, et al. A novel extension to the polynomial basis functions describing Bézier curves and surfaces of degreewith multiple shape parameters[J]. Applied Mathematics and Computation, 2013, 223: 1-16.

[4] LI J C. A novel Bézier curve with a shape parameter of the same degree[J]. Results in Mathematics, 2018, 73(4): 159.

[5] ZHU Y P, LIU Z. A class of trigonometric Bernstein-type basis functions with four shape parameters[J]. Mathematical Problems in Engineering, 2019, 2019: 1-16.

[6] HU G, BO C C, WEI G, et al. Shape-adjustable generalized Bézier surfaces: construction and it is geometric continuity conditions[J]. Applied Mathematics and Computation, 2020, 378: 125215.

[7] CEYLAN A Y. Construction of a new class of Bézier-like curves[J]. Mathematical Methods in the Applied Sciences, 2020, 44(9): 7659-7665.

[8] 王文涛, 汪国昭. 带形状参数的均匀B样条[J]. 计算机辅助设计与图形学学报, 2004, 16(6): 783-788.

WANG W T, WANG G Z. Uniform B-spline with shape parameter[J]. Journal of Computer Aided Design & Computer Graphics, 2004, 16(6): 783-788 (in Chinese).

[9] HAN X L. Piecewise quartic polynomial curves with a local shape parameter[J]. Journal of Computational and Applied Mathematics, 2006, 195(1-2): 34-45.

[10] CAO J, WANG G Z. Non-uniform B-spline curves with multiple shape parameters[J]. Journal of Zhejiang University SCIENCE C, 2011, 12(10): 800.

[11] WANG X, GAO C C, JIANG C. Cubic uniform B-spline curve and surface with multiple shape parameters[J]. Applied Mechanics and Materials, 2014, 543: 1860-1863.

[12] 刘华勇, 李璐, 谢新平, 等. 带局部形状参数的代数三角样条曲线曲面的构造[J]. 小型微型计算机系统, 2017, 38(3): 620-624.

LIU H Y, LI L, XIE X P, et al. Construction of algebraic and trigonometric spline curves and surfaces with local shape parametric[J]. Journal of Chinese Computer Systems, 2017, 38(3): 620-624 (in Chinese).

[13] ZHU Y P, HAN X L. A class of spline curves with four local shape parameters[J]. Acta Mathematicae Applicatae Sinica, English Series, 2017, 33(4): 979-988.

[14] 王成伟. 形状可调的三次三角样条插值曲线及其在服装造型中的应用[J]. 北京服装学院学报: 自然科学版, 2020, 40(4): 30-34.

WANG C W. Cubic trigonometric spline interpolation curve with adjustable shape and its application in garment modeling[J]. Journal of Beijing Institute of Fashion Technology: Natural Science Edition, 2020, 40(4): 30-34 (in Chinese).

[15] HAN X L, YANG J. Piecewise polynomial curves with normalized derivatives[J]. Journal of Computational and Applied Mathematics, 2021, 388: 113290.

[16] AMMAD M, MISRO M Y, RAMLI A. A novel generalized trigonometric Bézier curve: properties, continuity conditions and applications to the curve modeling[J]. Mathematics and Computers in Simulation, 2022, 194: 744-763.

[17] HU G, WU J L. Generalized quartic H-Bézier curves: construction and application to developable surfaces[J]. Advances in Engineering Software, 2019, 138: 102723.

[18] 张莉, 刘静静, 檀结庆. 多形状参数的指数均匀B样条曲线曲面[J]. 图学学报, 2013, 34(3): 29-35.

ZHANG L, LIU J J, TAN J Q. Exponential uniform B-spline curves and surfaces with multiple shape parameters[J]. Journal of Graphics, 2013, 34(3): 29-35 (in Chinese).

[19] 严兰兰, 韩旭里. 形状及光滑度可调的自动连续组合曲线曲面[J]. 计算机辅助设计与图形学学报, 2014, 26(10): 1654-1662.

YAN L L, HAN X L. Automatic continuous composite curve and surface with adjustable shape and smoothness[J]. Journal of Computer-Aided Design & Computer Graphics, 2014, 26(10): 1654-1662 (in Chinese).

Representation of a kind of2continuous composite curve

YAN Lan-lan, SONG Xi-chen, WEI Zi-hua, XIE Lei

(College of Science, East China University of Technology, Nanchang Jiangxi 330013, China)

To meet the strict requirements for the control points made by the2continuity conditions of the Bézier curve and many existing extended Bézier curves with shape parameter, a2continuous composite curve representation method was proposed. The method could synthesize the advantages of the Bézier method and B-spline method, and its basis function had explicit expression. It was of the automatic smoothness as that of the B-spline method, easily possessing the end-point geometric characteristic of the Bézier curve. To this end, a set of basis function with six parameters was constructed. On this basis, a curve segment based on four control points was constructed according to the definition mode of the cubic Bézier curve. According to the -continuity conditions between the curve segments, a kind of composite curve on four-point piecewise scheme was constructed according to the definition mode of the cubic B-spline curve. The basis function was of total positivity, and contained the cubic Bernstein basis functions and the cubic B-spline basis functions that were determined by the node vector with the repetition degree of all internal nodes being one. The curve segment had the feature of convexity-preserving, endpoint position, and adjustable shape, and contained the cubic Bézier curve and the cubic B-spline curve segment as special cases. The definition of the composite curve could automatically ensure its2continuity at each junction. The composite curve could have end-point interpolation and end-edge tangency by setting some of its parameters as specific values. At this point, the composite curve still contained independent parameters used to adjust its internal shape.As long as the parameters of the composite curve were selected according to certain rules, the2continuous cubic B-spline curve could be reconstructed.

curve design; B-spline method; Bézier method; geometric continuity; shape parameter

TP 391.72

10.11996/JG.j.2095-302X.2022061057

A

2095-302X(2022)06-1057-13

2022-07-25；

：2022-10-13

国家自然科学基金项目(11261003，11761008)；江西省自然科学基金项目(20161BAB211028)；江西省教育厅科技项目(GJJ160558)

严兰兰(1982-)，女，教授，博士。主要研究方向为计算机辅助几何设计。E-mail：yxh821011@aliyun.com

25 July，2022；

13 October，2022

National Natural Science Foundation of China (11261003, 11761008); Jiangxi Natural Science Fund (20161BAB211028); Jiangxi Provincial Department of Education Science and Technology Project (GJJ160558)

YAN Lan-lan (1982-), professor, Ph.D. Her main research interest covers computer aided geometric design. E-mail：yxh821011@aliyun.com