计算机辅助拓扑设计——持续同调在几何设计和处理中的应用
2023-01-13董哲同蔺宏伟
董哲同,蔺宏伟
计算机辅助拓扑设计——持续同调在几何设计和处理中的应用
董哲同1,2,蔺宏伟1,2
(1. 浙江大学数学科学学院,浙江 杭州 310027;2. 浙江大学CAD&CG国家重点实验室,浙江 杭州 310058)
持续同调是一种计算不同尺度拓扑特征的有效方法。其从一簇向后包含的单纯复形序列中提取出拓扑特征的出现和消失时刻,并使用拓扑特征的“生命周期”来量化地衡量该特征的几何尺度和重要程度。拓扑特征的提取与应用在几何设计中扮演着重要角色,催生出了一些基于持续同调的几何设计研究。从持续同调特征的提取与基于持续同调的建模和优化两方面进行综述,在持续同调特征的提取方面,介绍了从点云和三角网格数据中提取拓扑特征的不同方法,总结了拓扑特征在部分几何设计问题中的应用路径。在建模和优化方面,综述了基于拓扑变换的单纯复形重建方法、拓扑可感知的曲面重建方法与基于持续同调的拓扑去噪和优化方法。
持续同调;拓扑特征提取;形状重建;去噪与优化;几何设计;拓扑设计
1 绪 论
持续同调以计算几何和代数拓扑为主要数学工具,从一簇向后包含的单纯复形序列中计算各维同调等价类出现和消失的时刻,并将出现-消失点对作为复形序列拓扑特征。持续同调的提出和发展可以追溯到20世纪90年代。“持续性”(persistence)的概念独立地出现在了几乎处于同一时期的3组研究项目中,即学者Frosini,Ferri及其合作者的工作,学者Robins的博士论文和学者EDELSBRUNNER的项目[1]。2000年,美国Duke大学的学者EDELSBRUNNER等[2]系统地提出了持续同调的定义和算法,此后持续同调理论和计算方面的研究不断涌现,如文献[3-4]分别给出了持续同调和多维度持续同调的理论和计算方法。2009年,CARLSSON[5]的奠基性工作使得拓扑数据分析(topological data analysis)作为新兴的研究领域得以诞生。值得一提的是,持续同调与Morse理论有着紧密的联系,如持续性可以用于简化Morse-Smale复形的拓扑结构[6],Morse理论也可加速持续同调的计算[7]。持续同调可用于从采样点云推断采样流形可能的拓扑结构,从定义在单纯复形上的一类标量函数导出的单纯复形序列中提取各维度的拓扑特征。该方法能定量地反映拓扑特征的几何尺度,区分重要拓扑特征和噪声特征,对输入数据中的微小噪声和扰动不敏感。基于以上优点,持续同调在解决分子结构分析[8]、脑与神经科学[9]、医学图像处理[10]等领域的一些科学问题上获得了成功的应用。
计算机辅助几何设计是一门由微分几何、数值计算等数学分支与计算机交叉而产生的学科,主要以三维物体表示、建模、处理、分析和模拟为研究重点。从20世纪70年代以来,自由曲线曲面的表示、设计、显示、分析和处理等是计算机辅助几何设计的主要研究对象和内容[11],并取得的丰富研究成果,为三维建模软件的开发应用建立了理论基础。然而,由于缺乏有效的计算工具,在几何设计和处理中出现的一些拓扑问题,无法得到有效的系统解决方法。随着以持续同调(persistent homology)[2-3,5]为代表的计算拓扑技术的发展,三维形状的拓扑特征可以被量化地估计和表达,从而方便地应用于形状分析、分类与检索、拓扑可控的优化与建模等几何设计问题中。持续同调的成功应用为众多的代数拓扑理论走向应用提供了潜在的可能性,为解决几何设计和处理中的拓扑问题提供可能的解决方案,从而为计算机辅助拓扑设计这一新兴研究领域提供了潜在的理论支持。
近十年以来,持续同调被系统应用于几何设计和几何处理,主要解决三维形状的拓扑特征提取、分析以及形状建模中遇到的拓扑相关问题,逐渐形成了计算机辅助拓扑设计这一研究领域。在三维形状拓扑特征提取方面,持续同调采用持续图(persistence diagram)[2]或持续条码(persistence barcode)[5]编码同调特征,研究者们将这些特征转化为关于持续图度量稳定且易于使用的向量化形式,以便进一步应用于形状分析、分类和检索等问题中。在三维形状建模方面,如何使用提取的拓扑特征恢复三维形状是近年来研究的一个热点问题之一。持续同调可以用于区分重要的拓扑特征和噪声特征,在保拓扑尖锐特征的优化中也发挥了重要作用。另外,通过持续同调构造的持续逆映射(persistence inverse mapping)[12]使得拓扑可控的建模技术得到了发展。
2 预备知识:持续同调
持续同调致力于从一簇向后包含的单纯复形序列中提取不同尺度和不同维度的拓扑特征,如连通分支(0维特征)、独立环结构(1维特征)和独立空腔结构(2维特征)等,并且反映这些特征随尺度参数变化的出现和消失情况,以此衡量这些拓扑特征的几何尺度和重要程度。单纯复形是用于计算持续同调的基本组合结构,一个单纯复形通常是指由点(0-单形)、线(1-单形)、三角面(2-单形)和四面体(3-单形)等不同维度的单形按照以下规则组合而成的复合结构:①单纯复形中任意单形的面(face)属于该单纯复形;②任意2个单形的交要么为空,要么为公共面。
为了从采样点云中推断采样形状的拓扑结构,需要依托点云建立一系列向后包含的单纯复形,也称过滤(filtration)。建立过滤的方法有很多,如文献[13-15]所示方法,其中Vietoris-Rips复形[13]较为常用。该方法的基本思想是在每一点上放置一个闭球,所有球的半径参数逐渐增加。在某一参数下,若存在个点,满足其闭球两两相交,则这个点构成一个(-1)-单形。另外,将定义在形状上的标量函数做线性逼近生成定义在对应单纯复形上的分片线性函数也能生成过滤,用于提取按该标量函数数值大小排列时单纯复形的拓扑结构变化信息。通常可以将单纯复形按照分片线性标量函数数值从小到大或从大到小排列分别生成下水平过滤或上水平过滤。值得一提的是,Zig-zag持续方法[16]的出现使得过滤不再局限于向后包含的单纯复形序列。
代数拓扑是持续同调采用的主要数学工具,其将单纯复形中的单形视为代数运算的算术元素。在单纯同调的简单情形下,第维的所有单形按照模2加法构成-链群C,其中的元素由一些-单形的算术组合构成,称为-链。为了反映从C到C-1元素的边界关系,定义边界算子¶:C→C-1,该算子将一个-链映射为其中每个单形所有(-1)-面的代数和形式,称为-链的边界。对于任意1,相邻2个维度的边界算子的复合为零算子,即¶°¶-1=0。为了代数地表示独立孔洞结构,定义边界算子¶的零空间Z={ÎC:¶=0}为闭链群,边界算子¶+1的像空间B={ÎC:$ÎC+1s.t.¶+1=c}为边缘链群。直观地,一个独立环结构是一类非边界闭链,即不是任何高维链边界的闭链。由于相邻边界算子复合为零,所以可以用商群Z/B定义同调群H,同调群中的元素表示独立环结构的等价类,是一类重要的拓扑特征。同调群的阶(rank)称为Betti数,反映拓扑特征的个数,如0维Betti数指示单纯复形中连通分支的个数,1维Betti数指示独立环结构的个数。文献[17-18]提供了更多同调和计算同调的细节。
在过滤中,独立孔洞结构会随着参数变化而出现、存在和消失,持续同调能从过滤中计算同调特征的出现和消失对应的参数时刻,采用出生-死亡(birth-death)点对表示对应的同调特征。定义死亡值与出生值的差为持续值,该指标衡量拓扑特征的生命周期,以便推测该特征是否为采样形状的重要特征,并且衡量该特征的几何尺度。如图1所示,随着“时间参数”的增加,复形序列中陆续有拓扑特征出现和消失。图1(a)蓝色和橙黄色线段分别表示连通分支(0维拓扑特征)和独立环结构(1维拓扑特征)的生命周期,这些嵌入到平面中的线段构成了一个拓扑特征表示,称为持续条码。进一步,将出生-死亡点对嵌入到平面得到持续图,如图1(b)所示。持续图和持续条码为持续同调提供了紧凑的拓扑特征表示。另外,Wasserstein距离和bottleneck距离[14]可以用于度量2个持续图或持续条码之间的相似性。进一步,在满足不同条件时,持续同调具有一些稳定性结论[13,19-21],即当点云或形状上的标量函数发生扰动时,在这些距离的意义下,持续图或持续条码的扰动可以被该扰动的常数倍控制。这些稳定性结论说明了持续同调对数据中的噪声不敏感,在实践中具有重要的意义。
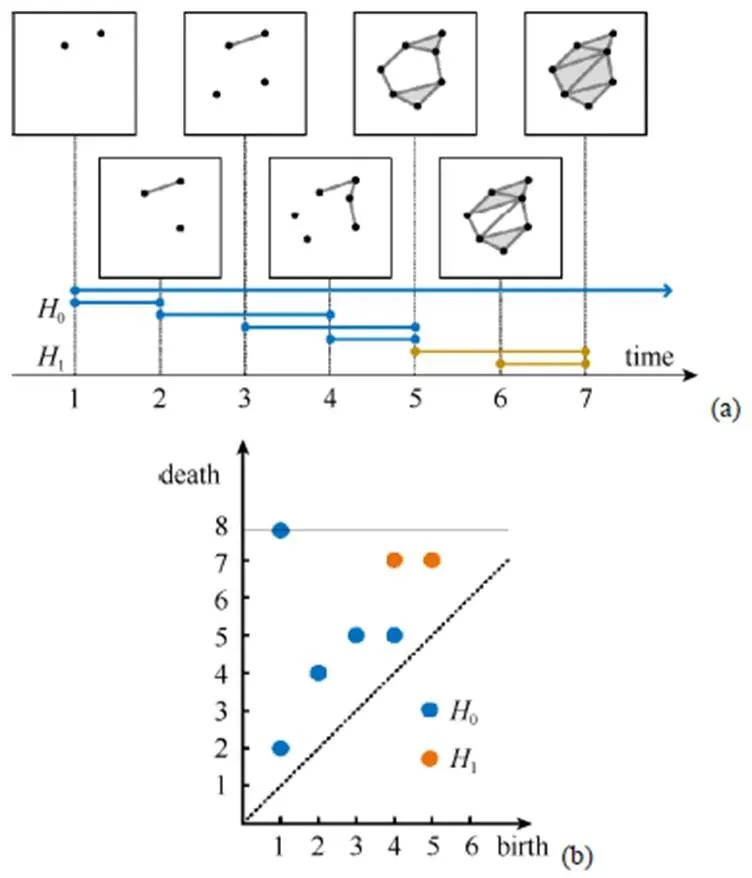
图1 使用持续同调从一簇向后包含的单纯复形序列中计算持续图的示意图((a)过滤与持续条码;(b)持续图)
过滤过程可以视作单形依参数大小依次添加到单纯复形中,单形的添加往往会对应某一拓扑特征的出现或消失。拓扑特征的出生值和死亡值分别对应2个不同的单形。文献[12]据此提出了拓扑逆映射来追踪持续点对对应的单形对,在形成过滤的标量函数满足一定条件时,可以构造良好定义的拓扑逆映射,该映射也可将持续点对映射为对应的临界点对。该映射是基于持续同调的拓扑可控方法的重要工具,据此可以计算有关持续图的目标函数关于标量场中各参数的梯度。如图2所示(虚线箭头给出了持续图上的点到拓扑空间上点对的映射关系),是定义在拓扑空间上的标量函数,按生成的下水平过滤计算持续图。持续逆映射将持续图上的点((),())映射到临界值点对(,),其含义是将对应的连通分支的出现追溯到点对应的单形在下水平过滤中的出现,将该连通分支的消失追溯到点对应的单形在下水平过滤中的出现[22]。
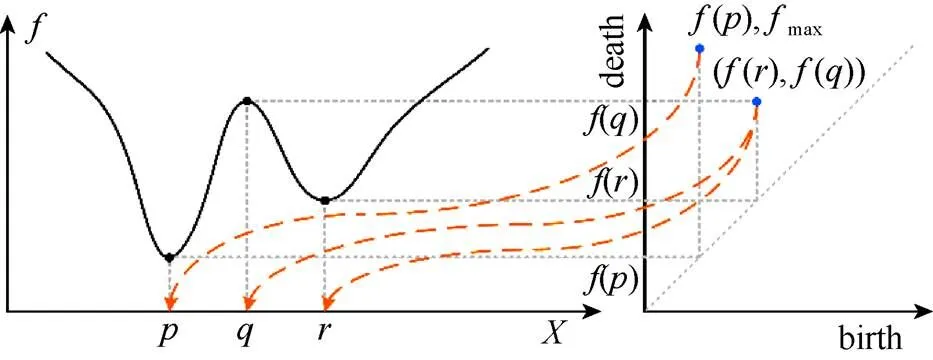
图2 持续逆映射的示意图[22]
3 持续同调拓扑特征及其应用
从几何形状中尽可能完整地提取形状某一方面或某几方面的特征是形状分析、分类和检索等几何处理问题中的重要步骤。传统的拓扑不变量,如Betti数、亏格和欧拉示性数等,虽然能提供拓扑特征的数量信息且便于计算,但是却不能具体地反映拓扑结构的几何尺度,对几何数据中的噪声非常敏感,即使局部扰动也会导致这些传统拓扑不变量的较大变化。持续同调能通过点云估计采样形状的拓扑结构,计算三维形状按某一标量函数生成过滤的拓扑特征。计算所得的持续图能将拓扑特征与形状的几何进行关联,提供几何尺度的量化指标,且对输入数据的噪声不敏感。本节综述使用持续同调从点云和空间网格中提取拓扑特征的相关方法,并总结拓扑特征表示在几何设计和处理中的应用。
3.1 点云的持续同调特征提取方法
空间点云是在三维空间中的一个点集,通常通过扫描或采样三维物体获得,是几何设计中一种常用的形状表示。一些几何设计任务需要提取点云中的拓扑特征进行分析,为了重建拓扑结构满足预期的三维形状,也需要从点云中提取拓扑先验信息。持续同调通过建立复形过滤的方式计算持续图,其中的点对分别表示复形序列中对应拓扑特征的出现和消失的参数时刻,而构造复形过滤有诸多方法。与Vietoris-Rips 复形类似,Čech复形[13]要求在单形的所有顶点对应的闭球有非空公共交集。Alpha复形[23]则通过Delaunay三角化生成关于点云的一组子复形。而当点云数据规模较大时,为了减少过滤中单纯复形的单形数量且反映单纯复形的主要拓扑结构,Witness复形[14]通过保留关键点和采样的方式构造近似复形过滤。另外,在构造Vietoris-Rips复形的过程中,可以通过点云下采样或设置最大半径参数的方式来近似地计算持续图[24]。
在大规模空间点云数据上计算持续同调是一个具有挑战性的任务,其主要困难在于随着点云中点个数的增加,计算较高维的持续同调特征需要考虑的单形个数将以指数增加。如按照Vietoris-Rips复形构造过滤,对一个含有5 000个点的空间点云,计算1维持续图须构造约107个1-单形和2×1010个2-单形[25]。持续同调算法的时间复杂度与单形个数成比例,即经典的持续同调算法在实例中具有拟线性的复杂度,而对于最坏情况,则具有关于单形个数的三次方的时间复杂度[2-3]。因此,需要通过设计数据结构、优化存储空间和并行计算等提高实际计算持续同调的效率[26],如Ripser[24]工具包提供了高效计算Vietoris-Rips复形序列的算法,文献[27-28]给出了高效构造单纯复形的数据结构,并简化了高维的单纯复形。
在点云处理中,往往只需要通过点云估算采样形状的大致拓扑特征,持续值较小的拓扑特征往往被视为噪声。因此,采用搭建神经网络来估计持续图成为了提升持续同调计算效率的一个新途径。SOM等[29]在提取图像特征时率先提出了一种基于卷积神经网络的架构估算持续图的向量化表示。在三维点云处理领域,文献[25]基于EdgeConv 卷积层[30]提出了一种快速估计点云Vietoris-Rips 复形过滤的持续图向量化表示持续图像(persistence images)[31]的网络架构。该神经网络使用大量点云数据及对应的持续图向量化表示作为训练数据,能端到端高效地估计持续同调特征。实验表明,估计所得的持续图像与真实持续图像偏差较小。但是该网络架构依赖于在点云上建立图结构,在理论上未说明关于点云数据的噪声和扰动具有稳定性。DE SURREL等[32]基于Deep sets[33]提出了一种快速估计点云的Vietoris-Rips复形过滤的持续图的网络架构。该方法借助Deep sets的理论结果可以简洁地推导出估计持续图的稳定性结论,且估计过程高效,计算结果也较为精确。由于在评估实验中,此类方法多使用点云标准数据集或合成数据集,因此尚不清楚此类方法在真实、复杂数据集上的表现。
3.2 三角网格的持续同调特征提取方法
空间三角网格表示的三维形状可以视为嵌入到空间的单纯复形。除了使用单纯同调计算Betti数或同调生成元或使用点云采样并计算持续同调获得拓扑特征以外,还有一些方法可用于提取三角网格的拓扑特征,如基于网格测地距离的持续同调方法,基于特征函数过滤的持续同调方法和拓扑变换方法。
与嵌入到空间的点云使用欧氏距离构造Vietoris-Rips复形类似,在三角网格上可以通过测地距离生成复形序列。CARRIÈRE等[34]提出了基于测地距离的持续同调方法来提取网格模型的拓扑特征。选择网格模型上的一点为圆心,以可变参数为半径作测地圆盘,可以得到在给定半径参数下完全包含在测地圆盘中的子复形。随着半径参数逐渐增加,得到一列向后包含的子复形序列,使用持续同调可以计算该复形过滤中持续图。对于三角网格上的任意一点,均可采取以上方法计算持续图,作为该三维形状的局部描述子。该方法提取的拓扑特征关于噪声不敏感,但需要定义相似性度量来比较2个三维模型对应的持续图簇之间的差异。
基于特征函数过滤的持续同调方法是提取网格模型特征的一类方法,即利用定义在这个网格上的标量函数按函数值大小生成复形过滤,计算持续同调。由于所选择的标量函数通常反映三维形状的局部特征,因此称这类标量函数为“特征函数”[35]。这类函数的选择往往依赖于实际应用,标量函数中参数的调整也多是经验性的。一般地,可以选择热核函数 (heat kernel signature)[36]或波核函数(wave kernel signature)[37]作为特征函数。如DONG等[38]使用热核函数设计多尺度拓扑描述子来分类多孔结构。文献[35, 39]也利用热核函数作为特征函数,以便将不同时间参数下的持续图组合为多尺度的描述子。
拓扑变换是一类将三维形状从形状空间转换到特征空间的方法。受启发于积分几何(integral geometry)[40]在曲面和随机场建模以及点云处理上的应用,TURNER等[41]提出持续同调变换(persistent homology transform,PHT)和欧拉示性变换(euler characteristic transform,ECT)提取网格的拓扑特征。PHT与ECT分别将网格模型(单纯复形)转换为一簇与不同投影方向相关的持续图与持续欧拉示性数,即使用不同的投影向量定义高度函数,再使用该函数构造复形过滤从而得到持续拓扑特征。持续欧拉示性数可以由持续图导出,因此PHT包含了ECT的全部信息。基于PHT的拓扑特征提取方法可以应用于网格对比与分类。根据PHT可以定义不同网格形状间的距离,即计算各方向上持续图的距离,并将距离值沿投影方向进行数值积分,以便度量网格的相似性。在ECT的基础上,CRAWFORD等[42]提出了光滑欧拉特征变换提取拓扑特征,并应用于癌症诊断以及针对形状的统计推断。KIRVESLAHTI和MUKHERJEE[43]将网格上的ECT推广到标量场上。对于一般的度量空间,OUDOT和SOLOMON[44]提出内蕴持续同调变换(intrinsic persistent homology transform,IPHT)提取特征。具体地,通过在度量空间中不同的点上定义距离场,IPHT利用距离场的下水平过滤生成持续图。与PHT的不同之处在于,IPHT与三维形状的嵌入空间无关,只与形状本身有关。
3.3 拓扑特征在几何处理中的应用
持续同调从三维点云和三角网格中提取拓扑特征,并以持续图的方式展示这些不同几何尺度的特征。然而,计算2个持续图之间的Wasserstein距离或bottleneck距离是比较耗时的,特别是当持续图中有大量的点对时,这是因为距离的计算依赖于点对集合之间的最优匹配的求解[45]。另外,诸多统计分析工具,如求平均值等,以及支持向量机等用于分类或聚类的机器学习常用工具不能以持续图作为输入,因此需要将持续图进行向量化,以便将这些拓扑特征应用于几何处理的相关问题中。
持续图的向量化可以分为将持续图转换为显式向量表示和隐式向量表示2类方法。持续图向量化的要点是转换得到的向量关于持续图的距离度量是稳定的,即持续图上的小扰动也对应着向量表示上的小扰动。显式向量化方法即将一个持续图映射到有限维向量空间的一个向量。这一类方法通常在持续图上构造特征曲面,使用与其等价的函数表示或将持续图嵌入到代数空间等,再进行离散化从而得到有限维向量表示。常用的特征曲面构造方法包括持续曲面[31]和持续B样条曲面[46];常用的持续图等价形式有持续Betti数函数[47]和持续景观 (persistence landscapes)[48]。离散化特征构造也有多种方式,如CANG等[49]通过直接划分持续图为均匀网格,并统计每个网格中持续点对的个数作为对应向量元素的值。文献[31]通过划分持续曲面的定义域并对每个曲面片积分得到向量中每一位的数值。另外,如Tropical坐标表示法[50]、持续词汇袋[51]和持续路径签名表示[52]等方法也是持续图向量化的有效方法。
持续图的隐式向量化通过非线性映射将持续图嵌入到合适的内积空间中,再在新的嵌入空间中训练线性模型来处理数据,该方法的核心是构造合适的核函数,因此又称此类方法为核方法。核方法不产生显式的向量化表示,也不显性地构造非线性映射。REININGHAUS等[53]提出持续尺度空间核函数,该核函数来源于一个热扩散问题,是一个多尺度的核函数。该向量化方法具有1阶Wasserstein稳定性,但不具备高阶Wasserstein稳定性。文献[21]提出持续加权高斯核,将持续图映射为希尔伯特空间中的元素。该向量化方法具有关于原始点云数据Hausdorff距离的稳定性。类似的核方法还有切Wasserstein核方法[54]和持续Fisher核方法[55]。最后,PUN等[56]对持续图向量化做了详细的综述。
图3总结了使用持续同调解决几何处理中的形状分析、分类和检索等问题的思路与流程。通过Vietoris-Rips复形等方法构造复形过滤,可以从点云中计算各维度的持续图;通过定义“特征函数”生成水平集过滤或者采用向各方向投影的PHT方法,可以计算持续图。将计算所得的持续图向量化的方法,使之与统计方法或机器学习方法兼容。最后,持续图的相关向量化表示被应用于形状比较[57-58]、形状匹配[12, 59]、形状检索[38, 60]、形状识别[61]、形状分类和分析[31, 62]中。
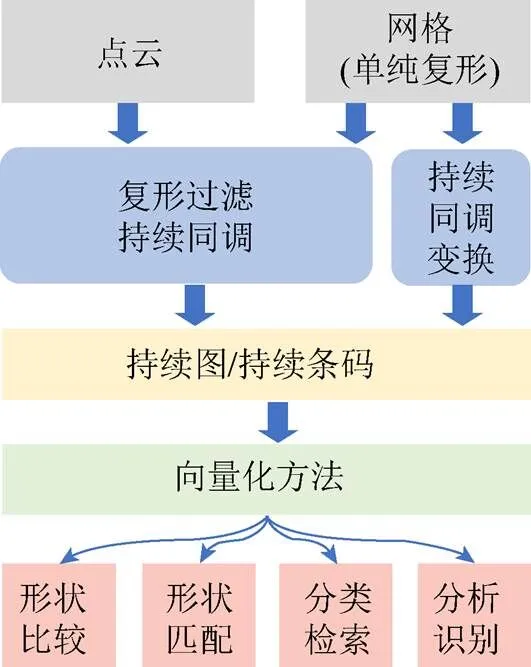
图3 从三维模型中提取持续同调特征并用于解决几何处理中一些问题的示意图
4 基于持续同调的建模和优化
三维形状的拓扑是一类重要的性质,也是几何设计关注的重要目标之一。相比于基于经典的离散拓扑不变量的拓扑可感知建模方法,持续同调为形状建模和优化提供了新思路。
4.1 基于拓扑特征的单纯复形重建
计算持续图是一个提取特征的过程,持续图是一组几何多尺度的拓扑特征,被应用于形状分类等几何设计问题中,而使用这些拓扑特征恢复和重建三维形状是一个逆向工程。PHT将一个单纯复形按照不同方向投影,产生一簇持续图。文献[41]从理论上证明了PHT在二维和三维空间上的单射性,即一簇持续图至多只与一个单纯复形对应。CURRY等[63]与GHRIST等[64]进一步推广了该结论,分别独立证明了在任意维度的欧氏空间中的可构造子集上,ECT具有单射性,并由此导出PHT的单射性。这意味着可以尝试从PHT产生的一簇持续图中恢复单纯复形。
文献[41]给出了PHT单射性的证明是构造性的,即从0维单形开始,逐步重建整个单纯复形。这事实上给出了重建单纯复形的算法,但该方法考虑的是从无穷多方向的持续图簇中重建单纯复形,因此这驱动了通过有限方向的持续图簇重建单纯复形的研究。文献[63]证明了有限个方向的持续图可以唯一确定形状,并给出了方向个数的上界。BELTON和TERESE[65]提出了从3个方向得到的拓展持续图出发,以多项式时间复杂度重建平面上的一维单纯复形(嵌入平面的图)的算法。算法通过搜索3组投影线的交点确定顶点,由顶点的“度”确定边。该算法的不足在于3个投影方向需由单纯复形本身确定,这使得该算法不具备通用性。进一步地,BELTON等[66]将算法从平面推广到任意维度欧氏空间,利用更多不同方向的持续图重建嵌入到任意维欧氏空间的一维单纯复形。FASY等[67]提出了增广持续同调变换(augmented PHT)的离散化方法,通过在单形上推广“入度”并研究单形预测技术,从而将这些方法扩展到从有限多个方向持续图重建任意维度的单纯复形。然而,上述方法缺乏在大型数据集上重建的实验结果。
4.2 拓扑可感知的三维建模
几何设计的一个重要研究课题是建模具有正确或理想的拓扑的三维形状。在部分研究中,往往采用后处理[68]或人机交互[69]的方式移除或修改生成形状上的拓扑错误,这些方式依赖于用户对形状进行局部修正。而部分研究[70-73]则通过使用亏格和Betti数等经典拓扑不变量设计约束条件,通过定义能量函数的方式优化组合单元,从而重建出拓扑正确的几何形状,如曲面。这类方法能保证生成具有拓扑不变量的形状,然而经典拓扑不变量不能描述拓扑特征的几何尺度,优化过程多采用动态规划,在一些复杂的算例中,算法的时间和空间复杂度会呈指数级。
基于持续同调的拓扑可感知方法利用文献[12]提出的持续逆映射建立一套基于梯度下降的连续优化框架。相比于基于经典拓扑不变量的离散优化框架,这类方法易于理解和实现,且可以使用能描述拓扑特征几何尺度的持续图作为重建和优化的先验信息。BRÜEL-GABRIELSSON等[74]提出了一种基于持续逆映射的拓扑可感知的从点云重建曲线和曲面的方法,根据持续图上点对的相对位置设计拓扑损失函数,并采用梯度下降的连续优化框架进行优化。具体而言,首先以点云中的点为中心的多元高斯函数构造似然函数,并将空间离散为自适应的单纯复形;使用该似然函数为每一个单形分配一个兼容的单形值;然后构造上水平过滤,计算持续图。最小化拓扑损失函数,计算损失函数关于似然函数中参数的梯度,使用梯度下降的方式更新参数;最后从优化后的似然函数对应的底复形中提取提升的同调表示元作为重建的曲线或曲面。由于该方法使用从似然函数中提取的同调表示元作为重建形状,所以曲线、曲面的光滑性不高。
为了提高重建曲面的光滑性并同时保障目标曲面具有预期的拓扑,文献[22]提出了一种基于持续逆映射的拓扑可控的隐式曲面重建方法。该方法首先计算点云的符号距离函数,离散包围盒为立方复形,并使用B样条函数拟合离散符号距离值;将重建目标对应的持续图作为拓扑预期用于设计拓扑目标函数;同样采用梯度下降的连续优化框架,最小化目标函数并优化B样条函数中的控制系数;最后根据优化后的持续图上主要特征点对的位置决定提取的等值面。该方法的优点在于可以通过优化控制水平集中较为显著的拓扑结构的几何尺度。如图4所示,通过最小化持续图上持续值第二大的点(绿色点)对应的持续值,该优化框架消除了较小尺度的环柄圈,且生成的隐式曲面具有较好的光滑性。该方法也有一些缺陷,如与其他基于梯度下降的连续优化框架类似,该优化方法可能会收敛到局部最优解,且每次优化迭代都需要计算持续图;不能很好地区分和优化较小的拓扑特征。
4.3 拓扑去噪与优化
图像与信号处理中的一个重要问题是研究如何在保留重要特征的同时去除数据中的噪声。同样地,拓扑去噪旨在保留拓扑尖锐点和尖锐边等特征,并且去除数据中的拓扑噪声。如CARR和SNOEYINK[75]通过提取输入数据的轮廓树并做简化以去除一些不必要的细微的拓扑特征,但该方法不能保证去除一些小的噪声环结构。另外一类常用的方法是基于Morse-Smale复形[76]的拓扑去噪和简化方法。如BREMER等[77]利用Morse-Smale复形消除(cancellation)技术简化复形结构,并在每次迭代过程中光滑单纯复形中单形内部的标量函数,从而保证调整后的单纯复形遵循一定的拓扑结构,并且生成光滑的二维标量场。然而该方法不能区分拓扑尖锐特征并进行保留。
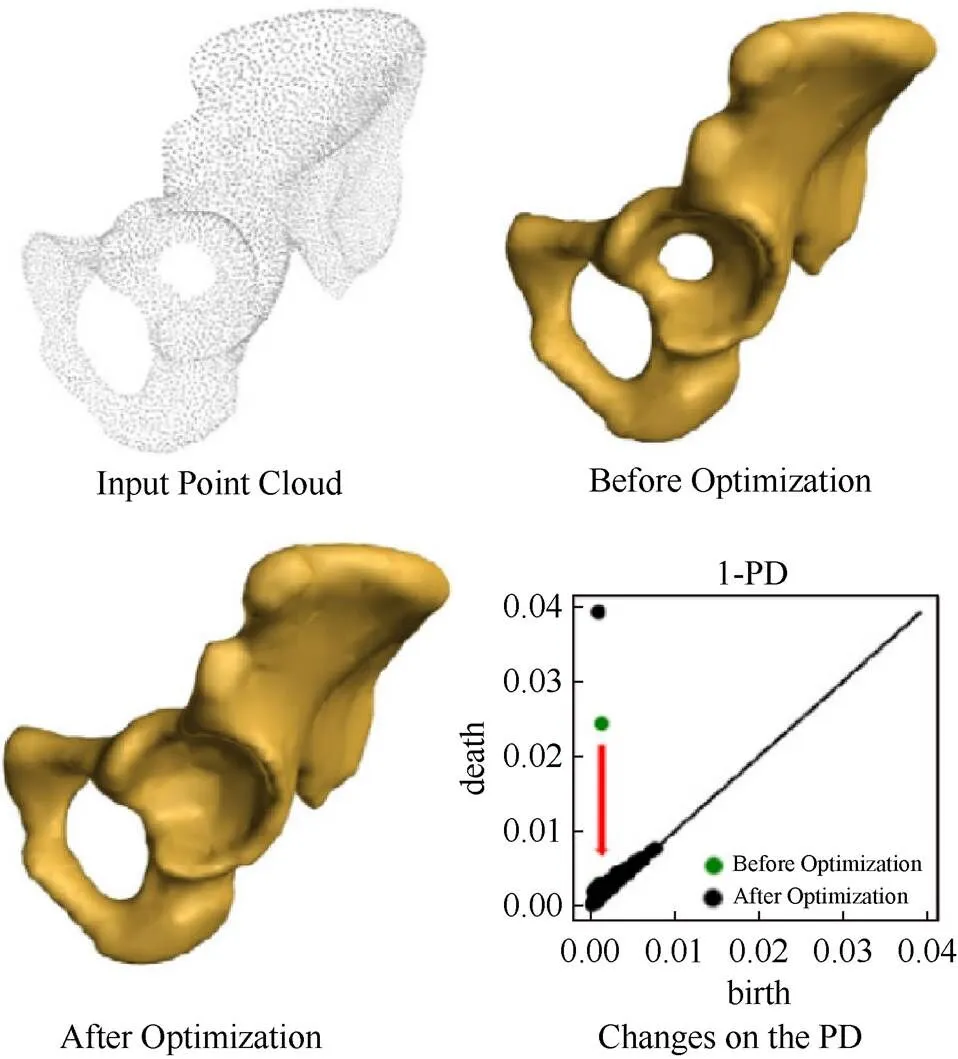
图4 文献[22]方法
为了保留重要拓扑特征并去除噪声,GÜNTHER等[78]利用持续同调为拓扑特征进行分级,将文献[79-80]提出的二维标量函数重建方法扩展到解决三维标量函数的去噪问题上。该方法首先计算标量场中的极值,从上/下水平过滤中计算持续图并按照持续值大小给极值点分级,确定拓扑尖锐点。再将拓扑去噪问题建模为离散优化问题,选定需要保留的拓扑尖锐点且避免新的尖锐点出现。采用线性化约束和凸化可行域的技术将优化问题转化为二次规划,并进一步转化为锥规划问题求解。在求解过程中,采用区域分解技术使得计算更加高效,内存使用更少,可快速地处理大规模标量场的去噪。但该方法是一种启发式算法,不能保证优化问题的解是全局最优解甚至局部最优解。
持续同调除了被用作优化过程中量化分级拓扑尖锐特征的工具外,还可以被用于设计保证拓扑结构正确的优化中。BRÜEL-GABRIELSSON等[81]将在文献[72]中提出的基于持续同调的拓扑可感知优化框架进行进一步推广,与机器学习技术相结合,应用于优化点云和体素的拓扑结构。对于三维体素数据,该方法并未给出过于复杂的算例,需要探索该框架在复杂拓扑数据场景下的应用。GAO等[82]提出了一种基于持续同调优化框架的保证连通性的多孔结构生成方法。该工作解决了通过多孔结构样本合成大尺寸多孔结构过程中不连通的问题。由于采用二值化体素建模多孔结构,无法直接使用梯度下降方法设计连续优化问题,因此该工作将基于距离场(distance to measure,DTM)的持续同调方法[83]推广到体素空间。DTM在空间位置上的取值与该位置与实体材料之间的距离呈正比,可以反映实体材料与空间位置的位置关系。该方法利用从DTM下水平过滤中计算得到的0维持续图设计优化目标,使得DTM中具有较小距离值的水平集具有一个连通分支,最终提取连通的立方复形作为优化后的多孔结构。图5展示了该方法使用持续同调优化框架优化多孔结构体素数据的实验结果。然而,与其他基于持续同调的拓扑可感知优化框架类似,该方法在每次迭代中均需要计算持续图,这增加了计算时间。

图5 文献[82]方法
5 总结与展望
一方面,自2000年文献[2]提出持续同调的基本概念以来,持续同调的理论体系得到了完善,并结合统计学和数据科学等其他学科,发展出了拓扑数据分析这一门新兴的交叉学科。另一方面,由于持续同调的发展建立在计算几何和计算拓扑的基础之上,所以在几何设计和处理领域也涌现出了大量持续同调的应用研究。本文首先简要地介绍了持续同调的发展历程和核心概念。在拓扑特征的提取和应用方面,综述了使用持续同调提取采样形状的点云和三角网格模型拓扑特征的方法,并总结了持续同调特征在形状分类、分析、匹配和检索等几何处理问题中的应用。另外,还从基于拓扑变换的单纯复形重建、拓扑可感知的三维曲面重建和拓扑去噪和优化3个方面综述了持续同调在形状建模和优化中的已有研究。
虽然持续同调在理论和应用方面取得了长足的发展和进步,但仍然有一些问题值得研究。文献[84-85]中列举了有关持续同调理论的公开问题。在应用方面,持续同调的高效和快速计算问题也值得研究。由于多维度持续同调[4]不存在紧凑的拓扑特征表示[86],如何提取和组织多层次拓扑特征是一个值得研究的问题。另外,基于持续同调的连续优化框架的理论也不断在完善[81, 87],更多的优化思路被不断地提出[88],为持续同调在几何设计中的应用奠定了坚实的基础。因此,基于持续同调的几何设计技术具有广阔的发展前景,并正在促进“计算机辅助拓扑设计”这一新兴研究领域的发展。
[1] EDELSBRUNNER H, HARER J. Persistent homology-a survey[J]. Contemporary Mathematics, 2008, 453: 257-282.
[2] EDELSBRUNNER H, LETSCHER D, ZOMORODIAN A. Topological persistence and simplification[C]//The 41st Annual Symposium on Foundations of Computer Science. New York: IEEE Press, 2002: 454-463.
[3] ZOMORODIAN A, CARLSSON G. Computing persistent homology[J]. Discrete & Computational Geometry, 2005, 33(2): 249-274.
[4] CARLSSON G, ZOMORODIAN A. The theory of multidimensional persistence[J]. Discrete & Computational Geometry, 2009, 42(1): 71-93.
[5] CARLSSON G. Topology and data[J]. Bulletin of the American Mathematical Society, 2009, 46(2): 255-308.
[6] ZOMORODIAN A J. Topology for computing[M]. Cambridge: Cambridge University Press, 2005.
[7] MISCHAIKOW K, NANDA V. Morse theory for filtrations and efficient computation of persistent homology[J]. Discrete & Computational Geometry, 2013, 50(2): 330-353.
[8] XIA K L, WEI G W. Multidimensional persistence in biomolecular data[J]. Journal of Computational Chemistry, 2015, 36(20): 1502-1520.
[9] LEE H, KANG H, CHUNG M K, et al. Persistent brain network homology from the perspective of dendrogram[J]. IEEE Transactions on Medical Imaging, 2012, 31(12): 2267-2277.
[10] QAISER T, TSANG Y W, TANIYAMA D, et al. Fast and accurate tumor segmentation of histology images using persistent homology and deep convolutional features[J]. Medical Image Analysis, 2019, 55: 1-14.
[11] 梁友栋, 刘鼎元, 金通洸. 计算几何的现状与趋势[C]//1982年计算几何讨论会. 杭州: 浙江大学学报, 1982: 17-25.
LIANG Y D, LIU D Y, JIN T G. Current status and trends in computational geometry[C]//Computational Geometry Symposium, 1982. Hangzhou: Journal of Zhejiang University, 1982: 17-25 (in Chinese).
[12] POULENARD A, SKRABA P, OVSJANIKOV M. Topological function optimization for continuous shape matching[J]. Computer Graphics Forum, 2018, 37(5): 13-25.
[13] EDELSBRUNNER H, HARER J. Computational Topology[M]. Providence, Rhode Island: American Mathematical Society, 2009.
[14] GUIBAS L J, OUDOT S Y. Reconstruction using witness complexes[J]. Discrete & Computational Geometry, 2008, 40(3): 325-356.
[15] ZOMORODIAN A. The tidy set: a minimal simplicial set for computing homology of clique complexes[C]//The 26th Annual Symposium on Computational Geometry. New York: ACM Press, 2010: 257-266.
[16] CARLSSON G, DE SILVA V. Zigzag persistence[J]. Foundations of Computational Mathematics, 2010, 10(4): 367-405.
[17] HATCHER A. Algebraic topology[M]. New York: Cambridge University Press, 2002.
[18] KACZYNSKI T, MISCHAIKOW K, MROZEK M. Computational Homology[M]. New York: Springer New York, 2004.
[19] COHEN-STEINER D, EDELSBRUNNER H, HARER J. Stability of persistence diagrams[J]. Discrete & Computational Geometry, 2007, 37(1): 103-120.
[20] CHAZAL F, DE SILVA V, OUDOT S. Persistence stability for geometric complexes[J]. Geometriae Dedicata, 2014, 173(1): 193-214.
[21] GENKI K, KENJI F, YASUAKI H. Kernel method for persistence diagrams via kernel embedding and weight factor[J]. Journal of Machine Learning Research, 2018, 18: 1-41.
[22] DONG Z T, CHEN J H, LIN H W. Topology-controllable implicit surface reconstruction based on persistent homology[J]. Computer-Aided Design, 2022, 150: 103308.
[23] EDELSBRUNNER H, MÜCKE E P. Three-dimensional alpha shapes[J]. ACM Transactions on Graphics, 1994, 13(1): 43-72.
[24] TRALIE C, SAUL N, BAR-ON R. Ripser.py: a lean persistent homology library for python[J]. Journal of Open Source Software, 2018, 3(29): 925.
[25] ZHOU C, DONG Z T, LIN H W. Learning persistent homology of 3D point clouds[J]. Computers & Graphics, 2022, 102: 269-279.
[26] OTTER N, PORTER M A, TILLMANN U, et al. A roadmap for the computation of persistent homology[J]. EPJ Data Science, 2017, 6(1): 17.
[27] ATTALI D, LIEUTIER A, SALINAS D. Efficient data structure for representing and simplifying simplicial complexes in high dimensions[C]//The 27th Annual Symposium on Computational Geometry. New York: ACM Press, 2011: 501-509.
[28] BOISSONNAT J D, MARIA C. The simplex tree: an efficient data structure for general simplicial complexes[J]. Algorithmica, 2014, 70(3): 406-427.
[29] SOM A, CHOI H, RAMAMURTHY K N, et al. PI-net: a deep learning approach to extract topological persistence images[C]//2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops. New York: IEEE Press, 2020: 3639-3648.
[30] WANG Y, SUN Y B, LIU Z W, et al. Dynamic graph CNN for learning on point clouds[J]. ACM Transactions on Graphics, 2019, 38(5): 1-12.
[31] HENRY A, TEGAN E, MICHAEL K, et al. Persistence images: a stable vector representation of persistent homology[J]. Journal of Machine Learning Research, 2017, 18: 1-35.
[32] DE SURREL T, HENSEL F, CARRIÈRE M, et al. RipsNet: a general architecture for fast and robust estimation of the persistent homology of point clouds[EB/OL]. [2022-01-25]. https://arxiv.org/abs/2202.01725.
[33] ZAHEER M, KOTTUR S, RAVANBAKHSH S, et al. Deep sets[EB/OL]. [2022-05-10]. https://arxiv.org/abs/1703.06114.
[34] CARRIÈRE M, OUDOT S Y, OVSJANIKOV M. Stable topological signatures for points on 3D shapes[J]. Computer Graphics Forum, 2015, 34(5): 1-12.
[35] LI C Y, OVSJANIKOV M, CHAZAL F. Persistence-based structural recognition[C]//2014 IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2014: 2003-2010.
[36] GĘBAL K, BÆRENTZEN J A, AANÆS H, et al. Shape analysis using the auto diffusion function[C]//Proceedings of the Symposium on Geometry Processing. New York: ACM Press, 2009: 1405-1413.
[37] AUBRY M, SCHLICKEWEI U, CREMERS D. The wave kernel signature: a quantum mechanical approach to shape analysis[C]//2011 IEEE International Conference on Computer Vision Workshops. New York: IEEE Press, 2012: 1626-1633.
[38] DONG Z T, PU J Y, LIN H W. Multiscale persistent topological descriptor for porous structure retrieval[J]. Computer Aided Geometric Design, 2021, 88: 102004.
[39] DEY T K, LI K, LUO C, et al. Persistent heat signature for pose-oblivious matching of incomplete models[J]. Computer Graphics Forum, 2010, 29(5): 1545-1554.
[40] KLAIN D A, ROTA G C. Introduction to geometric probability[M]. Cambridge: Cambridge University Press, 1997.
[41] TURNER K, MUKHERJEE S, BOYER D M. Persistent homology transform for modeling shapes and surfaces[J]. Information and Inference: A Journal of the IMA, 2014, 3(4): 310-344.
[42] CRAWFORD L, MONOD A, CHEN A X, et al. Predicting clinical outcomes in glioblastoma: an application of topological and functional data analysis[J]. Journal of the American Statistical Association, 2020, 115(531): 1139-1150.
[43] KIRVESLAHTI H, MUKHERJEE S. Representing fields without correspondences: the lifted Euler characteristic transform[EB/OL]. [2022-06-27]. https://arxiv.org/abs/2111.04788.
[44] OUDOT S, SOLOMON E. Barcode embeddings for metric graphs[J]. Algebraic & Geometric Topology, 2021, 21(3): 1209-1266.
[45] KERBER M, MOROZOV D, NIGMETOV A. Geometry helps to compare persistence diagrams[J]. ACM Journal of Experimental Algorithmics, 2017, 22: 1-20.
[46] DONG Z T, LIN H W, ZHOU C. Persistence B-spline grids: stable vector representation of persistence diagrams based on data fitting[EB/OL]. [2022-06-17]. https://arxiv.org/abs/1909.08417.
[47] FROSINI P, LANDI C. Persistent Betti numbers for a noise tolerant shape-based approach to image retrieval[J]. Pattern Recognition Letters, 2013, 34(8): 863-872.
[48] BUBENIK P. Statistical topological data analysis using persistence landscapes[J]. Journal of Machine Learning Research, 2015, 16: 77-102.
[49] CANG Z X, MU L, WU K D, et al. A topological approach for proteinclassification[J]. Computational and Mathematical Biophysics, 2015, 3(1): 140-162.
[50] KALIŠNIK S. Tropical coordinates on the space of persistence barcodes[J]. Foundations of Computational Mathematics, 2019, 19(1): 101-129.
[51] ZIELIŃSKI B, LIPIŃSKI M, JUDA M, et al. Persistence bag-of-words for topological data analysis[C]//The 28th International Joint Conference on Artificial Intelligence. New York: ACM Press, 2019: 4489-4495.
[52] CHEVYREV I, NANDA V, OBERHAUSER H. Persistence paths and signature features in topological data analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(1): 192-202.
[53] REININGHAUS J, HUBER S, BAUER U, et al. A stable multi-scale kernel for topological machine learning[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2015: 4741-4748.
[54] CARRIÈRE M, CUTURI M, OUDOT S. Sliced Wasserstein kernel for persistence diagrams[C]//The 34th International Conference on Machine Learning - Volume 70. New York: ACM Press, 2017: 664-673.
[55] LE T, YAMADA M. Persistence fisher kernel: a Riemannian manifold kernel for persistence diagrams[C]//The 32nd International Conference on Neural Information Processing Systems. New York: ACM Press, 2018: 10028-10039.
[56] PUN C S, LEE S X, XIA K L. Persistent-homology-based machine learning: a survey and a comparative study[J].Artificial Intelligence Review, 2022, 55(7): 5169-5213.
[57] FROSINI P, JABŁOŃSKI G. Combining persistent homology and invariance groups for shape comparison[J]. Discrete & Computational Geometry, 2016, 55(2): 373-409.
[58] DI FABIO B, LANDI C. Persistent homology and partial similarity of shapes[J]. Pattern Recognition Letters, 2012, 33(11): 1445-1450.
[59] DEY T K, LI K, LUO C, et al. Persistent heat signature for pose-oblivious matching of incomplete models[J]. Computer Graphics Forum, 2010, 29(5): 1545-1554.
[60] ZEPPELZAUER M, ZIELIŃSKI B, JUDA M, et al. A study on topological descriptors for the analysis of 3D surface texture[J]. Computer Vision and Image Understanding, 2018, 167: 74-88.
[61] BONIS T, OVSJANIKOV M, OUDOT S, et al. Persistence-based pooling for shape pose recognition[M]//Computational Topology in Image Context. Cham: Springer International Publishing, 2016: 19-29.
[62] ZHOU Z, HUANG Y Z, WANG L, et al. Exploring generalized shape analysis by topological representations[J]. Pattern Recognition Letters, 2017, 87: 177-185.
[63] CURRY J, MUKHERJEE S, TURNER K. How many directions determine a shape and other sufficiency results for two topological transforms[EB/OL]. [2022-05-19]. https://arxiv.org/abs/1805.09782.
[64] GHRIST R, LEVANGER R, MAI H. Persistent homology and Euler integral transforms[J]. Journal of Applied and Computational Topology, 2018, 2(1): 55-60.
[65] BELTON R L, TERESE B. Learning Simplicial Complexes from Persistence Diagrams[EB/OL]. [2022-05-08]. https://par. nsf.gov/biblio/10073868.
[66] BELTON R L, FASY B T, MERTZ R, et al. Reconstructing embedded graphs from persistence diagrams[J]. Computational Geometry, 2020, 90: 101658.
[67] FASY B T, MICKA S, MILLMAN D L, et al. The first algorithm for reconstructing simplicial complexes of arbitrary dimension from persistence diagrams[EB/OL]. [2022-05-29].https://arxiv.org/abs/1912.12759v2.
[68] ATTENE M, CAMPEN M, KOBBELT L. Polygon mesh repairing: an application perspective[J]. ACM Computing Surveys, 2013, 45(2): 15.
[69] YIN K X, HUANG H, ZHANG H, et al. Morfit: interactive surface reconstruction from incomplete point clouds with curve-driven topology and geometry control[J]. ACM Transactions on Graphics, 2014, 33(6): 202.
[70] SHARF A, LEWINER T, SHAMIR A, et al. Competing fronts for coarse–to–fine surface reconstruction[J]. Computer Graphics Forum, 2006, 25(3): 389-398.
[71] ZHOU S Z, JIANG C Y, LEFEBVRE S. Topology-constrained synthesis of vector patterns[J]. ACM Transactions on Graphics, 2014, 33(6): 215.
[72] HUANG Z Y, ZOU M, CARR N, et al. Topology-controlled reconstruction of multi-labelled domains from cross-sections[J]. ACM Transactions on Graphics, 2017, 36(4): 1-12.
[73] LAZAR R, DYM N, KUSHINSKY Y, et al. Robust optimization for topological surface reconstruction[J]. ACM Transactions on Graphics, 2018, 37(4): 46.
[74] BRÜEL-GABRIELSSON R, GANAPATHI-SUBRAMANIAN V, SKRABA P, et al. Topology-aware surface reconstruction for point clouds[J]. Computer Graphics Forum, 2020, 39(5): 197-207.
[75] CARR H, SNOEYINK J. Path seeds and flexible isosurfaces - using topology for exploratory visualization[EB/OL]. [2022-06-20]. https://dl.acm.org/doi/abs/10.5555/769922. 769927.
[76] DE FLORIANI L, FUGACCI U, IURICICH F, et al. Morse complexes for shape segmentation and homological analysis: discrete models and algorithms[J]. Computer Graphics Forum, 2015, 34(2): 761-785.
[77] BREMER P T, HAMANN B, EDELSBRUNNER H, et al. A topological hierarchy for functions on triangulated surfaces[J]. IEEE Transactions on Visualization and Computer Graphics, 2004, 10(4): 385-396.
[78] GÜNTHER D, JACOBSON A, REININGHAUS J, et al. Fast and memory-efficienty topological denoising of 2D and 3D scalar fields[J]. IEEE Transactions on Visualization and Computer Graphics, 2014, 20(12): 2585-2594.
[79] JACOBSON A, WEINKAUF T, SORKINE O. Smooth shape-aware functions with controlled extrema[J]. Computer Graphics Forum, 2012, 31(5): 1577-1586.
[80] WEINKAUF T, GINGOLD Y, SORKINE O. Topology-based smoothing of 2D scalar fields with C1-continuity[J]. Computer Graphics Forum, 2010, 29(3): 1221-1230.
[81] BRÜEL-GABRIELSSON R B, NELSON B J, DWARAKNATH A, et al. A topology layer for machine learning[EB/OL]. [2022-06-19]. http://proceedings.mlr.press/v108/gabrielsson20a. html.
[82] GAO D P, CHEN J H, DONG Z T, et al. Connectivity-guaranteed porous synthesis in free form model by persistent homology[J]. Computers & Graphics, 2022, 106: 33-44.
[83] ANAI H, CHAZAL F, GLISSE M, et al. DTM-based filtrations[M]//Topological Data Analysis. Cham: Springer International Publishing, 2020: 33-66.
[84] FERRI M. Persistent topology for natural data analysis—a survey[M]//Towards Integrative Machine Learning and Knowledge Extraction. Cham: Springer International Publishing, 2017: 117-133.
[85] GASARCH W, FASY B T, WANG B. Open problems in computational topology[J]. ACM SIGACT News, 2017, 48(3): 32-36.
[86] CERRI A, FROSINI P. Necessary conditions for discontinuities of multidimensional persistent Betti numbers[J]. Mathematical Methods in the Applied Sciences, 2015, 38(4): 617-629.
[87] LEYGONIE J, OUDOT S, TILLMANN U. A framework for differential calculus on persistence barcodes[J]. Foundations of Computational Mathematics, 2022, 22(4): 1069-1131.
[88] SOLOMON E, WAGNER A, BENDICH P. A fast and robust method for global topological functional optimization[EB/OL]. [2022-05-17]. https://arxiv.org/abs/2009.08496.
Computer aided topological design——survey on geometric design and processing based on persistent homology
DONG Zhe-tong1,2, LIN Hong-wei1,2
(1. School of Mathematical Sciences, Zhejiang University, Hangzhou Zhejiang 310027, China; 2. State Key Laboratory of CAD&CG, Zhejiang University, Hangzhou Zhejiang 310058, China)
Persistent homology is an effective method to compute topological features with different scales. It captures the birth and death time from a nested sequence of simplicial complexes, and employs the life span of a topological feature to measure its geometric scale and significance. The extraction and application of topological features play an important role in geometric design, spawning some studies on geometric design based on persistent homology. In this paper, we introduced the application studies in two aspects, i.e., the feature extraction of persistent homology and the persistent homology-based modeling and optimization. In the feature extraction of persistent homology, we introduced various methods for topological feature extraction from point clouds and triangular meshes, respectively. Meanwhile, the pipeline for applying topological features to some geometric design problems was summarized. In the persistent homology-based modeling and optimization, we reviewed the simplicial complex reconstruction methods based on topology transform, topology-aware surface reconstruction methods, and topological denoising and optimization based on persistent homology.
persistent homology; topological feature extraction; shape reconstruction; denoising and optimization; geometric design; topological design
TP 391
10.11996/JG.j.2095-302X.2022060957
A
2095-302X(2022)06-0957-10
2022-07-31;
:2022-10-16
国家自然科学基金项目(61872316,61932018)
董哲同(1995-),男,博士研究生。主要研究方向几何与拓扑设计。E-mail:ztdong@zju.edu.cn
蔺宏伟(1973-),男,教授,博士。主要研究方向为计算机辅助几何设计、计算机辅助拓扑设计、量子图形学等。E-mail:hwlin@zju.edu.cn
31 July,2022;
16 October,2022
National Natural Science Foundation of China (61872316, 61932018)
DONG Zhe-tong (1995-), PhD candidate. His main research interests cover geometric and topological design. E-mail:ztdong@zju.edu.cn
LIN Hong-wei (1973-), professor, Ph.D. His main research interests cover geometric and topological design, quantum graphics, etc. E-mail:hwlin@zju.edu.cn
