裂齿式永磁游标电动机性能分析与比较

杜 怿, 徐 晨

(江苏大学 电气信息工程学院, 江苏 镇江 212013)

随着电动机技术的发展，永磁同步电动机[1]、无刷直流电动机[2-4]等受到越来越广泛的关注和应用.采用具有低速、大转矩输出特性的永磁电动机构建直驱式系统，是提高运行效率、简化动力系统结构和降低故障率与维护成本的有效措施，在风力发电、电动汽车驱动[5-9]等领域受到了国内外学者的广泛关注.然而，为满足系统运行需求，直驱系统中的永磁电动机通常采用多槽、多极设计，导致该类永磁电动机的体积庞大、质量大和运输、安装困难等问题[10-11].

相比于传统永磁同步电动机(permanent magnet synchronous motor, PMSM)，永磁游标电动机[12](permanent magnet vernier motor, PMVM)基于调磁铁块将永磁磁场调制成一系列空间谐波磁场，并利用其中极对数少、转速高的有效谐波磁场和电枢绕组耦合，使得转子转速和电枢反应磁场转速之间形成转速差，实现所谓“自减速”运行，进而获得该类电动机低速、大转矩密度的输出性能[13]，符合直驱式系统的设计需求.因此，近年来，国内外学者对PMVM的运行原理、拓扑结构创新、优化设计和驱动控制等多个方面展开了较为深入的研究.通过与调磁式磁齿轮进行类比，W.N.FU等[14]、QU R.H.等[15]详细讨论了PMVM的运行原理，并揭示了二者之间的相互演化规律，得出了调磁式磁齿轮与PMVM运行原理的一致性结论.

从永磁体位置角度，可将PMVM分为定子永磁型和转子永磁型2大类.通过在定子轭部设置永磁体，香港理工大学S. L. HO等[16]提出了一种定子永磁型游标电动机，并对该类电动机的运行原理和电磁性能进行了讨论.通过比较，指出定子永磁型游标电动机在转矩密度和齿槽转矩等多个方面的不足.因此，国内外学者大多针对转子永磁型游标电动机进行研究.为了实现对永磁磁场的调制，PMVM通常需要设置调磁铁块，按照调磁铁块的位置，又可将转子永磁型游标电动机分为裂齿式和多齿式2大类[17].针对风力发电潜在应用，LI J.G.等[18]提出了一种外转子PMVM，采用裂齿式内定子结构，内侧表贴永磁体的外转子直接与风机连接，进而构成直驱式结构，有效缩短了机械能传递链，降低了机械损耗、提高了传输效率.而S.L.HO等[16]则基于磁路法推导出转矩方程，并基于转矩方程的定量分析提出了多齿式PMVM最大转矩设计方法，为该类电动机的优化与设计提供了理论基础.日本学者R. ISHIKAWA等[19]对多齿和裂齿式PMVM性能进行了对比研究，结果表明裂齿式结构有助于降低电流密度、利于散热，可有效降低电动机损耗、提高效率.LI J.G.等[20]利用解析法和有限元法就永磁磁场谐波、空载感应电势和电磁转矩等电磁性能，对裂齿式外转子PMVM与低速磁齿轮电动机进行了比较，结果表明裂齿式PMVM具有更高的空载感应电势和转矩，但该文献主要基于PMVM的永磁磁场展开，并未涉及电枢反应磁场和损耗等方面的内容.事实上，由于PMVM基于磁场调制原理运行，导致该类电动机气隙中含有大量不同极对数、不同旋转速度的谐波磁场，进而导致其铁耗和永磁体涡流损耗的复杂性.

为进一步揭示PMVM(特别是裂齿式PMVM)的性能优势，文中基于有限元仿真软件JMAG对1台外转子6槽32极裂齿式PMVM进行分析，并将其与具有相同直径、轴长、定子齿数的2台外转子PMSM进行比较.

1 电动机结构及工作原理

图1所示为文中所研究的裂齿式PMVM(电动机1)，6槽32极PMSM(电动机2)，6槽4极PMSM(电动机3).

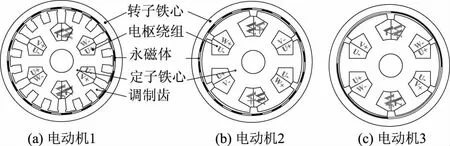
图1 电动机结构图

由图1可见，3台电动机结构类似，主要包括外转子和内定子2部分.外转子由永磁体和转子铁心组成，永磁体表贴于转子铁心内侧，采用径向充磁，且相邻永磁体的充磁方向相反.3台电动机的内定子均包含6个定子齿，用来绕制电枢绕组.裂齿式PMVM在PMSM的基础上，将6个定子齿齿靴加厚，并在齿靴处开一定深度的小槽，形成圆周分布的等宽小齿充当调制齿，形成了裂齿式结构.

令Pr1、Ps1、Pr2、Ps2、Pr3、Ps3分别为电动机1、2、3的永磁体极对数、电枢绕组极对数，裂齿式PMVM基于磁场调制原理运行，其参数应满足：

Ns=Pr1±Ps1，

(1)

式中：Ns为调磁齿个数.电动机1的极槽配比为Ns=18，Pr1=16对，Ps1=2对.

PMSM电枢绕组极对数等于永磁体极对数，以实现永磁磁场和电枢磁场相互耦合和有效的机电能量转换，故电动机2和3的电枢绕组与永磁体极对数相等，且Pr2=Ps2=16对，Pr3=Ps3=2对.

3台电动机的电枢绕组连接方式如图2所示，都采用双层绕组.

图2 绕组连接方式

为了统一对比分析，3台电动机的转子外径、内径、轴向长度分别为103、91、80 mm，定子外径、内径分别为88、20 mm，永磁体厚度为2.5 mm，气隙长度为0.5 mm，线径1.74 mm，额定电流10 A，槽满率0.5 mm，均保持一致.相比于电动机2和3，电动机1采用裂齿式结构，齿靴和调磁齿在径向占据相对较大空间，故电动机1的槽面积最小，电枢绕组匝数最少，3台电动机的半槽面积依次为367.9、432.0、432.0 mm2，匝数则依次为110、128、128匝.所用主要材料如下：永磁体材料采用N33UH(1.200 T)；定、转子铁心采用50JN470.

2 电磁性能分析

本节采用二维有限元仿真对3台电动机的基本电磁特性进行计算和分析.考虑到3台电动机均采用表贴永磁体结构，d、q轴电感相等，为了获取最大的电流利用率，文中采用了id=0的驱动策略.

2.1 气隙磁密分析

图3给出了电动机1的气隙磁密及谐波频谱.如图3a和3b所示，忽略高次谐波分量，主要含有2对极、16对极和20对极谐波分量，其中，16对极谐波幅值最大，由转子上永磁体直接产生，幅值为1.030 T.而2对极和20对极谐波由转子上永磁体的永磁磁场经调制齿调制后产生，其幅值分别为0.192、0.126 T.从图3d可见，2对极谐波的幅值最大，为0.210 T，其次是4对极和16对极谐波，幅值分别为0.110、0.070 T.图4为电动机1永磁磁场和电枢磁场中上述主要谐波相位随转子位置的变化情况.图中P为极对数.

图3 电动机1永磁和电枢磁场气隙磁密及谐波频谱

图4 电动机1永磁和电枢磁场主要谐波相位变化

由图4可见，永磁磁场气隙磁密中的2对极、16对极和20对极谐波与电枢磁场气隙磁密中相同极对数的谐波相位始终相差90°，根据电机学理论，这些谐波均能分别相互作用并产生有效转矩，因此均被称为工作谐波.

同理，可计算电动机2和3的永磁磁场和电枢磁场气隙磁密，并进行相应的频谱分析，结果如图5-8所示.将3台电动机的气隙磁密谐波分析结果进行汇总，如表1所示.

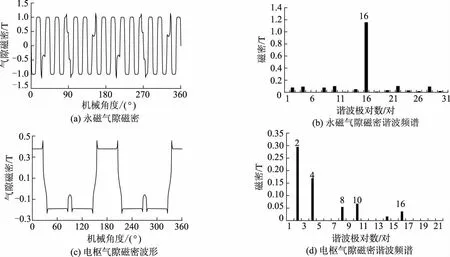
图5 电动机2永磁和电枢磁场气隙磁密及谐波频谱

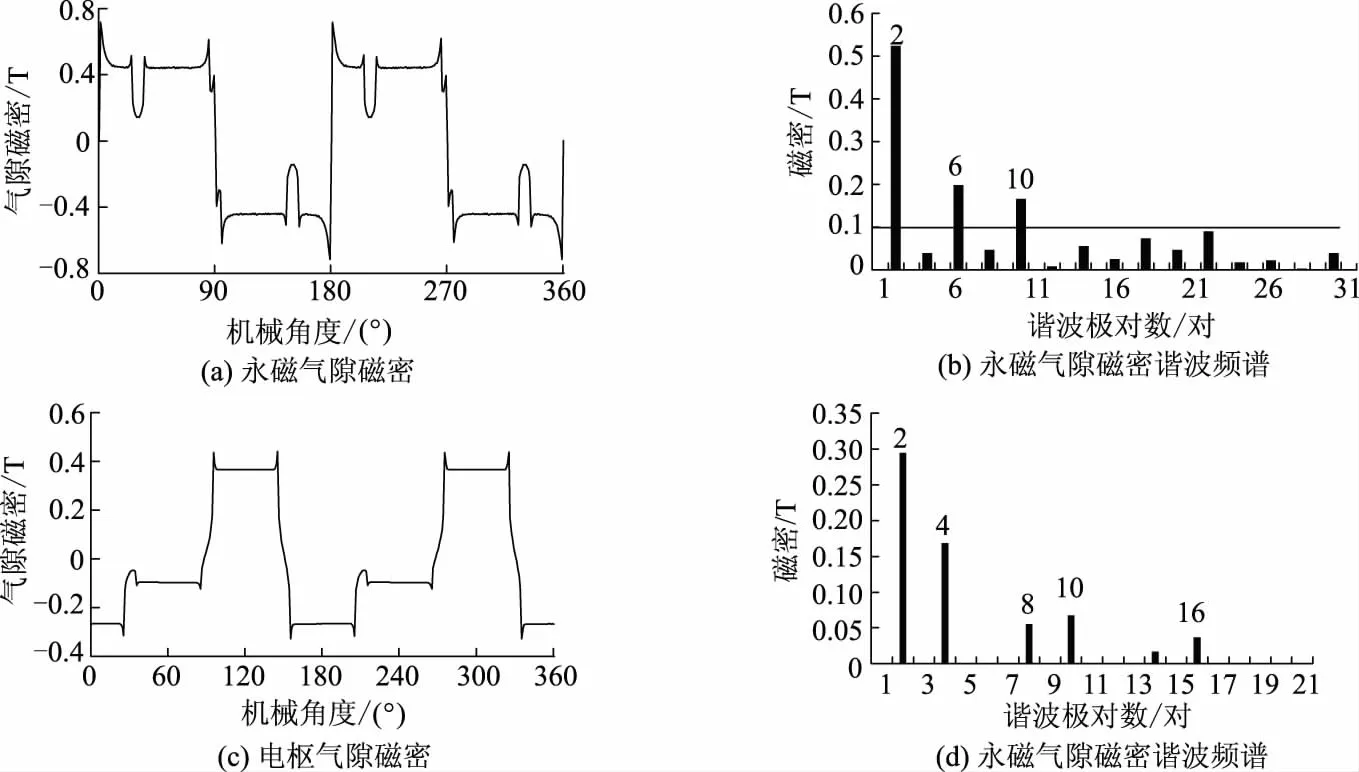
图6 电动机3永磁和电枢磁场气隙磁密及谐波频谱

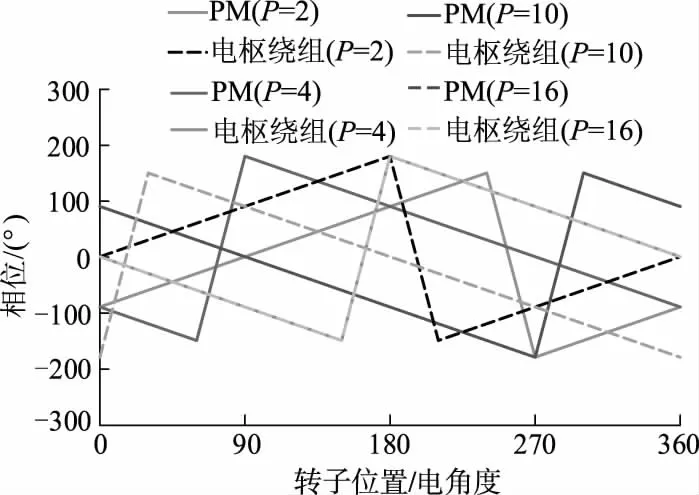
图7 电动机2永磁和电枢磁场主要谐波相位变化

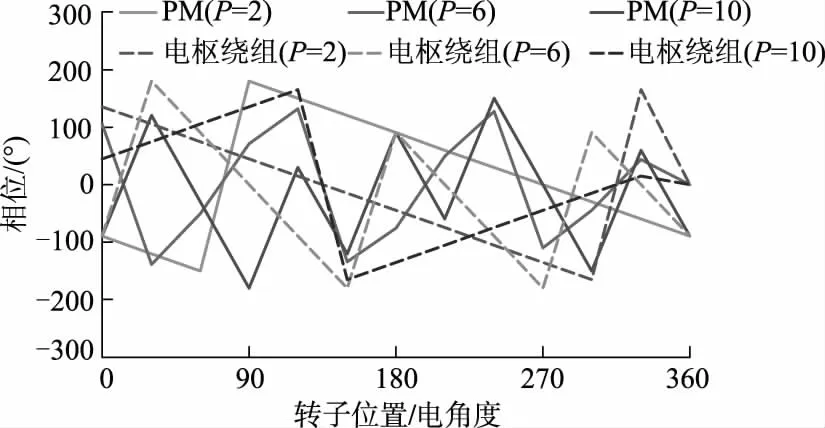
图8 电动机3永磁和电枢磁场主要谐波相位变化

表1 气隙磁密谐波分析结果

由表1可见，3台电动机的电枢磁场气隙磁密谐波成分差别不大，因此主要针对永磁磁场进行分析.电动机1和2中，永磁磁场气隙磁密主要谐波含量均为有效分量，为这2类电动机产生较高的转矩密度提供了基础.相比而言，电动机3永磁磁场气隙磁密中，除2对极谐波为有效分量外，其余均为无效分量，而且，这些无效分量的幅值与2对极分量为同一数量级，导致该类电动机的转矩密度较小.此外，电动机1和2中均包含幅值超过1 T的16对极谐波，该谐波导致定子铁心内部磁场发生高频变化，进而导致较高的定子铁心损耗；而电动机3中，幅值最大的分量为2对极，相比上述16对极分量而言，由其导致的定子铁心内部磁场的变化频率仅为1/8，因此理论上电动机3的铁耗应最小.

2.2 转矩分析

根据电动机学基本原理可知，由气隙磁密谐波分量产生的单个线圈永磁磁链可表示为

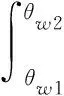
(2)

式中：Pj为第j次谐波的极对数；Bjmax和θj(t)为第Pj对极谐波的幅值和相位；rsi为电动机内定子外径；N为单个线圈的匝数；la为轴长；θw1和θw2为单个线圈两边的机械角度；θ为转子位置角.

根据式(2)可对3台电动机的单相永磁磁链进行计算.表2为各主要工作谐波产生的磁链幅值.

表2 主要工作谐波产生的磁链幅值 mWb

由表2可见，电动机1中绕组匝链的永磁磁链主要由2对极和16对极谐波分量产生，而电动机2和3中的绕组空载磁链则分别由16对极和2对极谐波磁场产生，相比而言，由于电动机3转子上仅包含2对永磁体，永磁体极距远大于电动机1和2，因此，其磁链幅值最大.为证明理论计算的正确性，表2中还列出了基于有限元计算得到的单相绕组磁链峰值，相应的磁链波形如图9所示，可见计算值和仿真值基本一致.

图9 磁链波形

图10为3台电动机转速为600 r·min-1时单相绕组的空载感应电势波形.

图10 空载感应电势波形

由图10可见，计算值和仿真值波形具有较高的吻合度.其中，电动机1的空载感应电势波形正弦度最高，且幅值最大，而电动机3的空载感应电势幅值最小，这是由于电动机3的永磁体极对数远小于电动机1和2，导致其磁链变化频率较低导致.忽略电流换向产生的扰动转矩，永磁电动机的电磁转矩Te由永磁转矩TPM、磁阻转矩Tr及定位力矩Tcog组成.由于文中采用id=0控制，磁阻转矩为0，故电动机的电磁转矩可表示为

(3)

式中：ψPM为绕组中永磁磁链的峰值；iq为绕组中q轴电流分量；Pr为转子极对数.

图11给出了定位力矩波形.

图11 定位力矩波形

由图11可见，电动机1定位力矩很小，可忽略不计.电动机2和3的定位力矩分别为3.27、2.11 N·m.由式(3)可直接计算出3台电动机的转矩平均值分别为67.87、38.30、16.90 N·m.图12为3台电动机的转矩仿真波形.

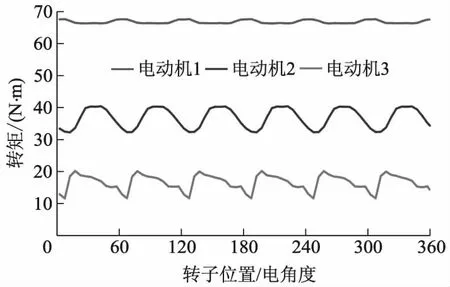
图12 转矩波形

由图12可见，3台电动机的额定转矩平均值分别为66.79、36.70、15.83 N·m，均与计算值十分接近，相应的转矩脉动分别为2.1%、22.2%、51.8%.图13为不同电流密度下的峰值电磁转矩图.由图13可见，当电枢电流小于额定值(3 A·mm-2)时，3台电动机的转矩均与电流幅值呈线性关系.而当电流大于3 A·mm-2时，受铁心饱和的影响，电动机2的转矩增幅率先趋缓，紧接着，电动机1的转矩也趋于平缓，而电动机3的转矩则始终保持与电流的线性关系，表明电动机3具有最佳的短时过载能力.文中在计算时选择的电流密度为3 A·mm-2，图14为3台电动机的磁密云图.

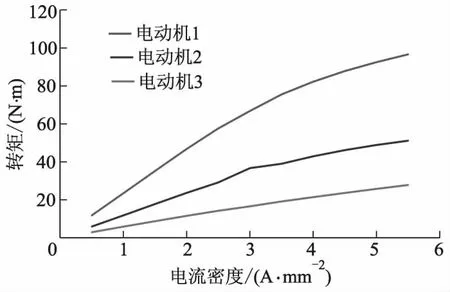
图13 不同电流密度下峰值转矩波形

图14 电流密度为3 A·mm-2时磁密云图

由图14可见，3台电动机的磁通密度幅值大部分均不超过1.60 T, 电动机1齿靴部分略微饱和，但幅值不超过1.90 T，电动机3转子轭部有部分饱和，幅值不超过2.24 T.

2.3 损耗分析

忽略机械损耗，电动机的损耗主要包括定转子铁心损耗、电枢绕组铜耗和永磁体涡流损耗.其中，铁耗和永磁体涡流损耗主要由永磁和电枢磁场中与铁心和永磁体具有相对运动的谐波磁场分量产生.

表3汇总了3台电动机在相同转速时的铁耗.

表3 3台电动机铁耗汇总 W

由表3可见，首先，由于永磁体均安装于转子铁心内侧并随转子铁心一同旋转，因此，3台电动机的定子铁耗均大于转子铁耗；其次，电动机1和2的铁耗比电动机3大得多，这是由于电动机1和2内含有极对数较大的16对极谐波分量，定子铁心内部磁场发生高频变化导致的.可见损耗仿真结果与上文基于气隙磁密谐波成分对损耗的分析结果一致.

图15为3台电动机永磁体涡流损耗的仿真波形.由于电动机3中永磁磁场谐波分量极对数较小，因此其永磁体涡流损耗较小；而电动机1基于磁场调制原理运行，导致永磁体内部磁通密度变化较大，在永磁体内部形成了较大的涡流损耗.

图15 3台电动机永磁体涡流损耗

效率是电动机的关键参数之一，忽略机械摩擦损耗和附加损耗值时，电动机效率可表示为

η=Pout/(Pout+PCu+PFe+PPM)，

(4)

式中：Pout、PFe、PPM、PCu分别为电动机输出功率、铁耗、永磁体损耗和绕组的铜耗.

表4汇总了3台电动机的铁耗、铜耗、永磁体损耗、输出功率以及效率，可以看到相应的效率分别为89.2%、83.7%、87.5%.

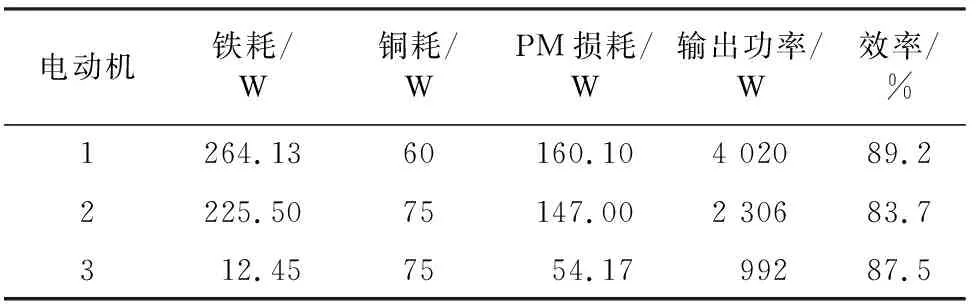
表4 损耗与效率

3 结 论

1) 电动机1和2中，永磁磁场气隙磁密主要谐波含量均为有效分量，为这2类电动机产生较高的转矩密度提供了基础.电动机3永磁磁场气隙磁密中，除2对极谐波为有效分量外，其余均为无效分量，该类电动机的转矩密度较小.

2) 相比电动机2和3，电动机1的平均转矩分别增加约45.0%、76.2%，转矩脉动减小约90.5%、95.0%，进一步揭示了裂齿式PMVM齿槽转矩低、转矩密度高和转矩脉动小的优势.

3) 相比于电动机2和3，电动机1基于磁场调制原理运行，导致永磁体内部磁通密度变化较大，在永磁体内部形成了较大的涡流损耗.由于裂齿式PMVM基于磁场调制原理运行，较大极对数的谐波分量使得定子铁心和永磁体内部磁场高频变化，导致其铁耗和永磁体损耗较大，可能会对电动机平稳运行造成不良影响.