河源降水重现期方法对比及暴雨致灾危险性分析

钟东良，曾钦文，谭 哲，贺发胜，魏兰华

(1.河源市气象局，广东 河源 517000；2.连山壮族瑶族自治县气象局，广东 连山 513200； 3.紫金县气象局，广东 紫金 517400)

1 概述

河源地形以山地、丘陵为主，属南亚热带海洋性季风性气候[1]，山地占53%，丘陵36%，谷地和平原占11%，罗浮山脉呈现东北-西南走向并贯穿全境，九连山脉延申至广州白云山一带，另有莲花山支脉延至紫金县东南部。强降水云团移至河源上空时，容易受地形抬升影响，水汽形成辐合，造成降水效率较高，从而诱发极端暴雨事件，造成发山体滑坡、泥石流等灾害。人民生命和财产安全，受到严重威胁。

近年来，我国极端降水事件明显增加，且具有显著区域性特征[2-3]。其中，蒋鹏等[4]研究发现，河源所在的粤东北地区为降水异常区，存在多个不同时间尺度的周期振荡；林蓉璇[5]等曾运用Arcgis对广东省暴雨洪涝灾害进行风险区划；古霖[6]等利用Pearson-Ⅲ分布对年最大日降水量的重现期分析；李国景[7]采用指数分布分析最大日降水量估算重现期与数值上大体相近；钟美英等[8]利用指数分布法对最大日降水量及年降水量的重现期进行分析；李珊珊[9]等显示Gumbel分布函数可以较好地估算广东省热带气旋降水重现期；唐传师等[10]采用Gumbel-I型极值分布对江西暴雨不同重现期的降水极值进行分析；钟东良[11]曾基于不同重现期降水对粤东北暴雨灾害风险的影响做过研究探讨；另有不同地方的学者通过指数分布法、Gumbel-I型分布法进行拟合计算重现期，在暴雨致灾危险区划方面取得不少成果。但是，基于暴雨重现期为致灾因子对河源暴雨致灾危险区划方面的研究较少，同时暴雨致灾危险区划的研究对于目前当地防灾减灾部署有科学意义。

综上所述，前人在研究降水重现期分析方面采用多种极值分布，其结果呈现不同程度的拟合优势。为揭露河源市的降水变化规律和特征，本文采用卡方检验法挑选最优的重现期极值分布法研究河源市暴雨致灾危险性，研究结果有利于提升地方各级政府及相关部门暴雨灾害防御能力，科学开展风险管控和隐患排查工作，同时对做好河源市防灾减灾服务工作并贯彻落实“人民至上、生命至上”理念有积极意义。

2 研究资料和方法

本文采用Matlab软件，以河源5个国家基本气象站1966—2019年日最大降水量为样本，分别通过指数分布法、Gumbel-I型分布法进行拟合计算得出多年一遇日最大降水量估算值，并进行卡方检验法对比选出最优拟合分布法。再以2010—2020年河源市近百个自动气象站日最大降水量为样本，用最优拟合分布法计算出5年、10年、20年、30年、50年、100年一遇日最大降水量估算值，并通过Arcgis绘制出不同重现期下河源暴雨致灾危险区划进行分析讨论。

3 基于年最大日降水量的重现期曲线拟合

3.1 两种重现期分布法的编程

降水重现期为暴雨发生频率的倒数，通常指大于某暴雨强度的降雨出现一次的平均间隔时间，以某年一遇表示。本文使用Matlab对各分布法进行编程计算。

1) Gumbel-I型分布法分布形式为：

X=β-α*lgT(X)

(1)

式中：

α——尺度参数；

β——分布密度参数。

编程关键部分如下所示：

a=s1/s2;

ux=avg_x-a*avg_y;

x0=1:1000;

T=1-1./x0;%极值分布

Gumbel_x=ux-a*log(-log(T));

figure

plot(x0,Gumbel_x)

title('日最大降水量多年一遇极值曲线')

2) 指数分布法分布形式为：

x=rlnA+β

(2)

式中：

r——离散程度参数；

β——分布曲线下限；

A——特定再现期极值。

编程关键部分如下所示：

T_avg=sum(T)/num;

d1=abs(x-avg);

d2=abs(log(T)-log(T_avg));

A=[sum(d1.*d2),sum(d2.^2)];

a=A(1)/A(2);

b=avg-a*log(T_avg);

x0=1:1000;

latT=a*log(x0)+b;

plot(x0,latT)

title('日最大降水量多年一遇极值曲线')

3.2 重现期曲线拟合对比检验

令T=1～1 000 a，间隔为1 a，推算不同重现期下可能出现的曲线走势(见图1，和平站分布曲线省略)。由图1可知：在相同重现期下，4个国家站最大日降水量的Gumbel-I型、指数曲线走向一致，Gumbel-I型曲线陡峭，指数分布法曲线相对平缓，其中龙川站年最大日降水量两种分布函数在相交后呈发散状态最为显著，Gumbel-I型分布相较于指数分布，其发散趋势较大。在相同重现期下降水量值优度拟合表现为耿贝尔Ⅰ型分布>指数分布。由预测降水量可知：1～1 000 a年最大日降水量预测上线分别为河源站450 mm，龙川站400 mm，紫金站350 mm，连平站300 mm。

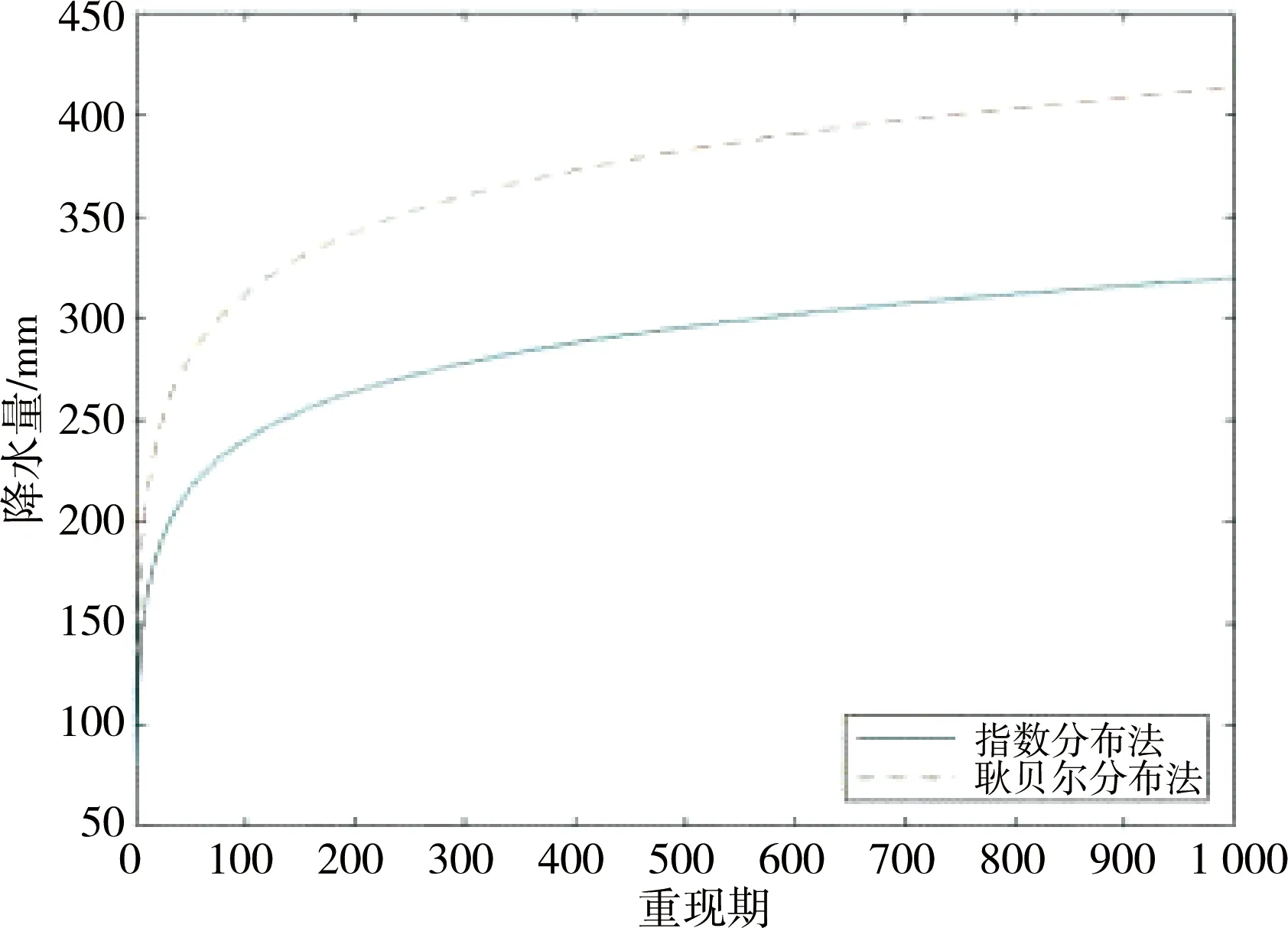
a 河源站

本文通过用卡方检验对样本和重现期降水量进行拟合检验对比，其中卡方检验是一种非参数检验法[12-13]，广泛应用于分类变量的独立性检验中，也可用于分类变量的比较检验，统计样本的实际观测值与理论推断值之间的偏离程度。其结果越小，则偏离程度越小，从而确定最优分布函数。本文通过用卡方检验进行拟合检验对比所得结果见表1所示。

由表1可知，4个国家站检验结果均大于0.05信度，均通能过卡方检验，其中Gumbel-I型分布法卡方检验所得结果相较于指数分布法所得结果较小，更接近于实际值，可见用Gumbel-I型分布法所得结果与样本拟合度相对较高，可使用Gumbel-I型分布法所得结果对河源不同重现期降水量暴雨致灾危险区划进行下一步分析。

表1 两种降水重现期计算方法的卡方检验结果

4 河源不同重现期降水量暴雨致灾危险区划分析

4.1 Gumbel-Ⅰ型分布法估算结果

本文使用Gumbel-Ⅰ型分布法进行拟合计算，其中估算重现期下的极值计算公式为：

(3)

式中：

a、β——尺度和位置的参数，其计算方式为：

a=1.282 5/σx,β=σx-0.577 2/a

(4)

式中：

rx、σx——观测所得N个实际值的平均值和均方差；

ry、σy——Gumbel-Ⅰ型分布中不同实际值的均值和均方差；

T——特定重现时间。

以2010—2020年河源市近百个自动气象站日最大降水量为样本，利用Gumbel-I型分布法计算出5年、10年、20年、30年、50年、100年一遇日最大降水量估算值，并以多年一遇日最大降水量估算值为致灾因子，通过Arcgis绘制出不同重现期下河源暴雨致灾危险区划，对结果对比分析。其中5个国家基本气象站不同重现期下日最大降水量计算结果如图2所示。

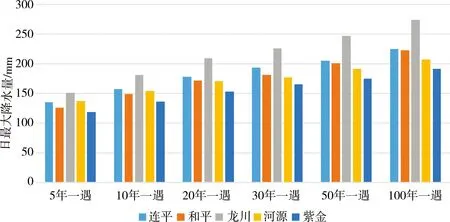
图2 河源5个国家基本气象站不同重现期日最大降水量示意

由图2可见，在不同重现期下，由Gumbel-I型分布法计算所得不同重现期日最大降水量可见，龙川站日最大降水量的估算值明显最多，紫金站则为最少。随着重现期增大，各站点估算值呈上升趋势，和平站的估算值随重现期增大，其上升幅度大于连平站上升幅度，且于20年一遇开始到100年一遇其估算值均大于河源站的日最大降水量估算值。

4.2 河源不同重现期下暴雨灾害危险性分析

用Gumbel-I型分布法计算出5年、10年、20年、30年、50年、100年一遇日最大降水量，以所得多年一遇日最大降水量作为致灾因子，利用GIS技术中反距离插值方法，得出河源不同重现期下暴雨灾害危险性区划和不同重现期暴雨灾害危险性不同风险区占比(见表2和图3)，以直观的方法探讨不同重现期下河源暴雨灾害危险性的变化趋势并加以研判分析。

由图3可见，东源县西侧、源城区的高风险分布随着重现期逐渐加大呈显著缩小趋势较明显；紫金县东南角、龙川县东部、和平县和连平县中北部高风险分布不同重现期下一直维持；东源县中部、和平县和连平县南部的一般风险区分布范围随着重现期增大，呈缩小趋势较明显；东源县东南侧与龙川县南侧、紫金县东北侧交界地区则在不同重现期下一直维持较低风险等级。

由表2可知，随重现期的加大，低和极低风险区占比总体呈加大趋势，一般风险区占比呈缩小趋势，高和极高风险区占比呈缩小趋势。从高到极高风险区分布特征可见，风险等级受地形因素影响较大，如连平、和平北部受九连山高山地形影响，锋面易受阻挡，往往成为雨窝点；同样紫金东南侧则受莲花山地形影响，受地形抬升作用，水汽易于此处产生辐合，造成降水效率较高。

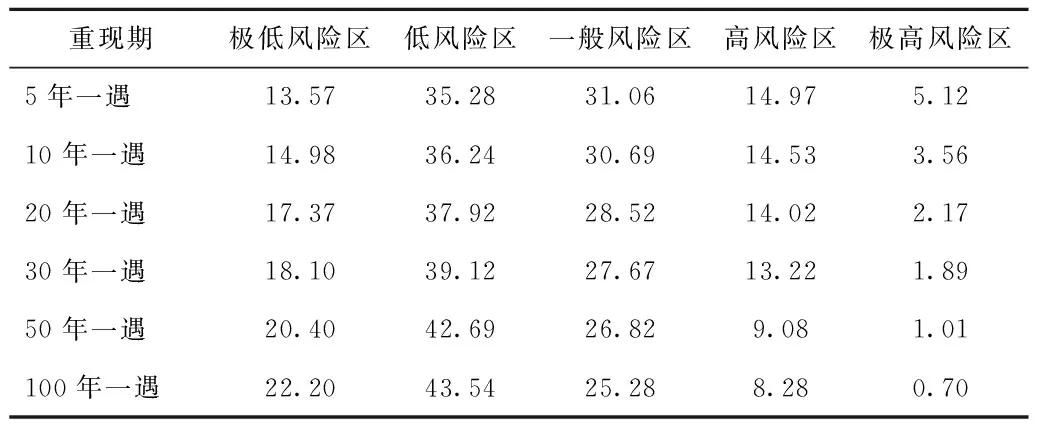
表2 不同重现期下暴雨灾害危险性各风险区占比 %

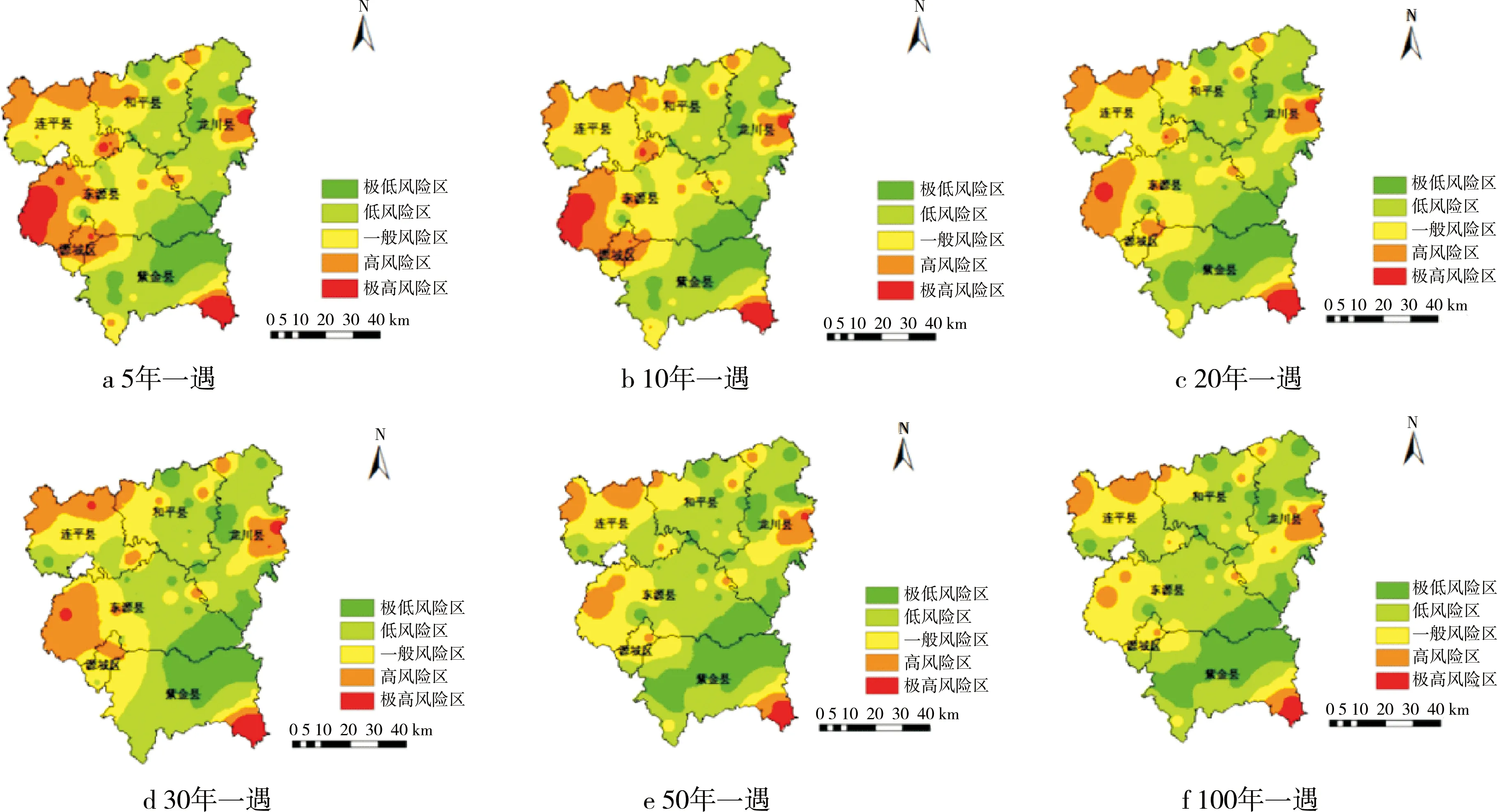
图3 河源5年、10年、20年、30年、50年、100年一遇日最大降水量示意

5 结语

1) 通过用卡方检验对样本和重现期降水量进行拟合检验对比，确定Gumbel-I型分布法相较于指数分布法而言拟合度更高，为研究当地暴雨灾害危险性更优极值分布方法。

2) 由Gumbel-I型分布法计算所得不同重现期日最大降水量可见，随着重现期增大，各站点估算值基本呈上升趋势。各风险区在不同重现期下存在明显变化趋势，具体表现为：高和极高风险区域在5年一遇中占比最高，随着重现期增大总体呈缩小趋势；低和极低风险区在100年一遇中占比最高，随着重现期增大占比呈增大趋势；一般风险区则随着重现期增大呈缩小趋势。