考虑上部结构与地基相互作用的行波效应研究

谢文斌

(广东省水利电力勘测设计研究院有限公司，广州 510635)

1 概述

地震作为地球内部活动所导致的地面震动，往往会对建筑产生不同程度的破坏。随着研究的深入以及技术的进步，抗震分析已经成为如今建筑结构设计过程中必不可少的一环。在一般的结构抗震分析中，地震力视为一致激励作用于结构计算模型底部，使得模型底部产生一致震动，在此基础上再进行结构在地震作用下的受力及变形分析。然而在实际工程中，由于地震波在土体中的传播有一定的速度，当遇到建筑水平投影长度较长和地质条件较差的情况，建筑结构实际的震动情况与一致激励的假设情况相差较大，此时，进行行波效应分析变得尤为关键。

行波效应是地震在传播过程中，由于时间与空间的变化，对建筑结构所产生的影响效应。行波效应分析的一般做法是在所要进行分析的上部结构底部(不考虑土体及地基)施加一定方向传播的多点激励荷载进行模拟分析[1-5]。但此方法由于忽略了地基刚度和传力的影响，其与实际情况还是存在着一定的差异。就此问题，张继承等人也做过相关研究，证明在静力荷载工况下，考虑上部结构与地基相互作用与只考虑上部结构相比，其上部结构构件的内力分布与内力峰值都有着一定的差别[6]。因此，范重等人采用一定刚度的弹簧约束模拟地基刚度，并研究对比了考虑地基刚度与不考虑地基刚度的多点激励分析结果，得出了考虑地基刚度后，进行多点激励分析时，框架柱内力可显著降低的结论[7]。郭乐天等人更是研究出采用钢框架及阻尼器来替代模拟土体的多点激励分析方法[8]。

本文结合湛江市赤坎水质净化厂(扩容提质)配套用房工程，在上部结构模型的基础上进一步地建立包含相关土体及其地基结构的有限元模型，并进行考虑上部结构与地基相互作用的行波效应研究，为今后的工程设计提供参考。

2 工程概况

湛江市赤坎水质净化厂(扩容提质)配套用房工程位于湛江市赤坎区振华路华田雅居北侧，总长约为74 m，总宽约为38 m，总高约为22 m，建筑总面积约为 5 995 m2，为地上6层框架结构。基础形式采用桩基础，桩长约31 m，为摩擦桩。

根据工程项目《详细勘察阶段工程地质勘察报告》(以下简称《详勘报告》)，场地主要由②淤泥、淤泥质土、③粉质黏土、黏土、④粉细砂、⑤中粗砂、⑥淤泥质土以及⑦粉质黏土、黏土组成，相关主要物理力学参数建议值见表1所示(表中没有的数据按经验取值)。计算分析采用钻孔如图1所示。

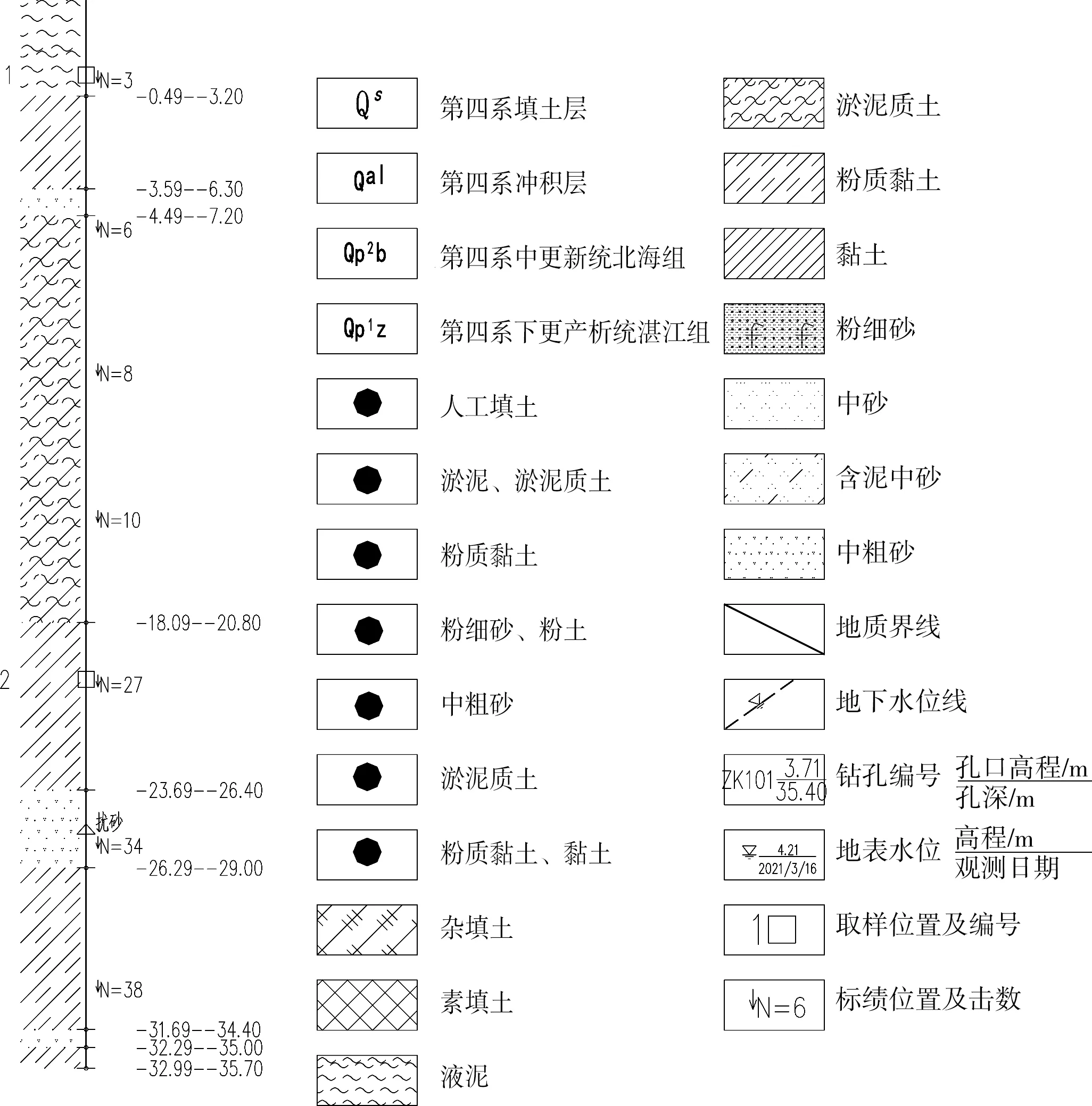
图1 计算分析用钻孔示意

另外，根据《详勘报告》中的场地评价，建筑场地属于抗震不利地段，相关等效剪切波速、场地土的类型以及场地类别划分见表2所示。

表2 等效剪切波速、场地土的类型和场地类别划分

3 行波效应分析

3.1 地震波选取

本工程抗震设防烈度为7度，设计地震分组为第一组，设计基本地震加速度为0.1g，建筑场地类别为Ⅱ类，特征周期Tg=0.45 s。根据《建筑抗震设计规范》[9](GB 50011—2010)(2016年版)(以下简称《抗规》)第5.1.2条选择7组时程分析法用地震波，其中5条天然波，2条人工波，分别为BIGBEAR-01_NO_907、CHI-CHI,TAIWAN-05_NO_2958、COALINGA-01_NO_364、TH003TG045_CHALFANT VALLEY-02 7-21-1986 BISHOP - LADWP(以下简称TH003TG045)、TH028TG045_CHUETSU-OKI 7-16-2007 NIIGATA NISHI KABA(以下简称TH028TG045)、RH2TG045以及RH4TG045。相关地震波主方向时程曲线如图2所示，相关时程分析基底剪力结果与CQC基底剪力结果比值见表3所示，相关时程曲线在结构主要振型的周期点上平均地震影响系数相差值如图3所示。

所示结果满足《抗规》：① “每条时程曲线的基底剪力为振型分解反应谱法(CQC法)的65%～135%且多条时程曲线的平均基底剪力为CQC法的80%～120%”的要求;② “多组时程波的平均地震影响系数曲线与振型分解反应谱法所用的地震影响系数曲线相比，在对应于结构主要振型的周期点上相差不大于20%”的要求。

3.2 模型建立及验证

此次分析中，考虑到正常设计情况，只考虑上部结构的行波效应分析采用Midas GEN 2020版进行计算，考虑上部结构与地基相互作用的行波效应分析采用Midas GTS NX 2021版进行计算。

分析模型建立过程：① 采用Midas GEN 2020建立上部结构模型；② 将Midas GEN 2020模型以MXT文件形式导出并导入Midas GTS NX 2021中；③ 采用Midas GTS NX 2021继续建立土体及地基模型。

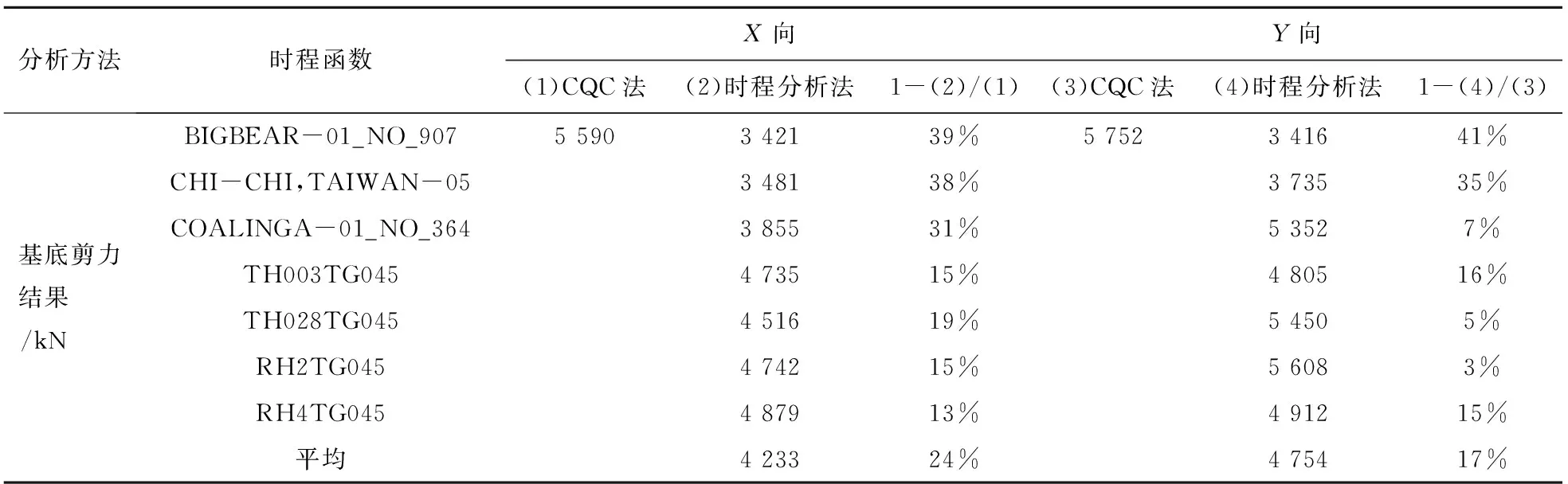
表3 反应谱与时程分析基底剪力对比(X方向)

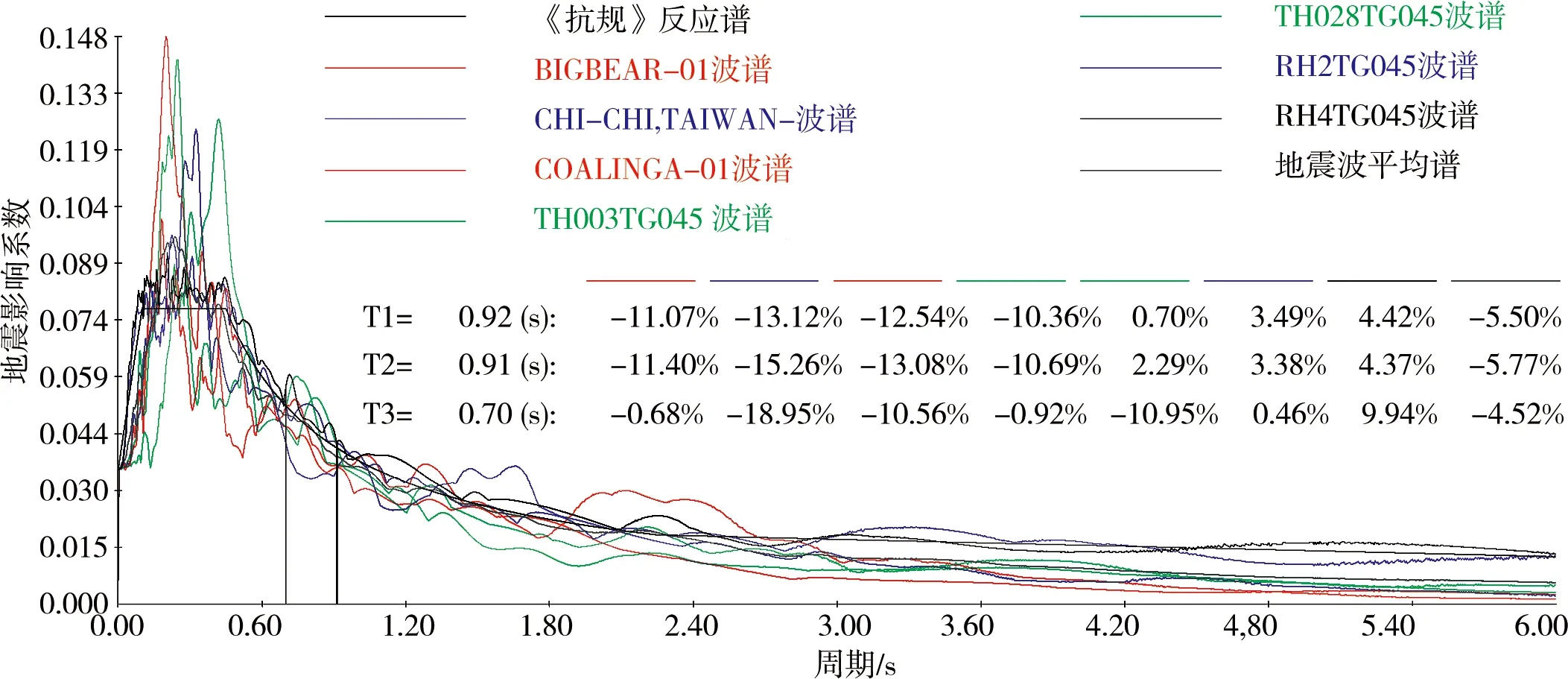
图3 各时程加速度谱与规范谱对比示意

在Midas GEN 2020建立的上部结构模型中(以下简称Midas GEN模型)，梁柱构件采用梁单元模拟，楼板采用板单元模拟，剪力墙采用墙单元模拟，模型总单元数为3 592。3层及3层以下采用C40混凝土本构模型，3层以上采用C30混凝土本构模型进行模拟，底部采用固接边界。模型长边为X向，短边为Y向，整体模型如图4所示。

在Midas GTS NX 2021建立的考虑上部结构与地基相互作用模型中(以下简称Midas GTS NX模型)，梁柱构件采用1D梁单元模拟，楼板采用2D板单元模拟，剪力墙采用2D板单元模拟，承台采用3D实体单元模拟，拉梁采用1D梁单元模拟，桩采用1D梁单元模拟，桩与土体的相互作用采用1D桩单元模拟，土体采用3D实体单元模拟，共145 059个单元。3层及层以下(不包括基础)采用C40混凝土本构模型，3层以上采用C30混凝土本构模型，基础部分的承台、拉梁以及桩采用C30混凝土本构模型，土体采用摩尔库伦本构模型进行模拟，其中土体材料的阻尼比为0.05[10-11]。

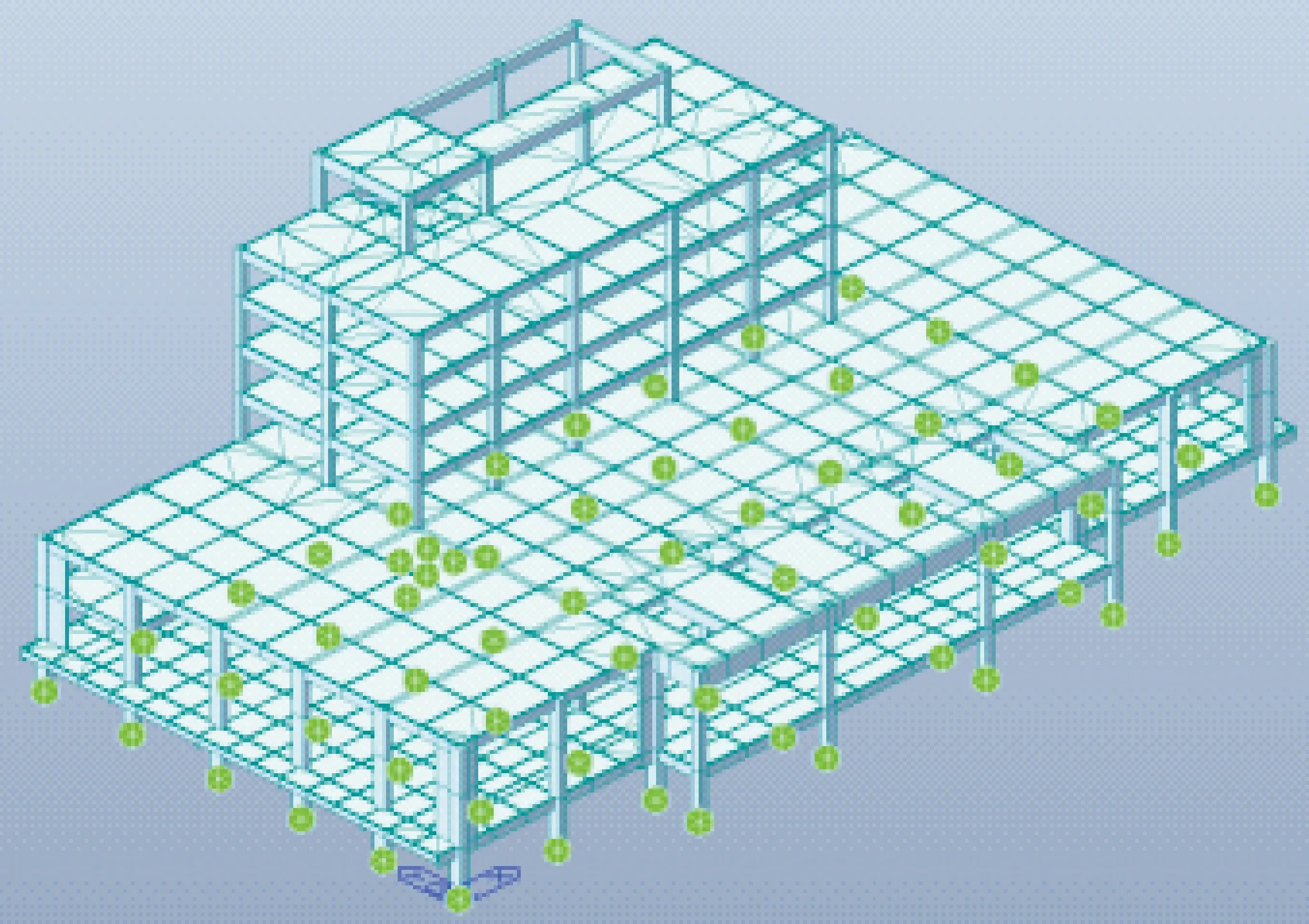
图4 Midas GEN上部结构模型示意

考虑到在动力分析中，如果土体四周采用侧向约束边界，边界会将地震波完全反射回模型中，而在实际情况中，建筑周围土体为无限大，周围土体并不会将地震波完全反射回模型中，因此，为了模拟所关注结构周围无限大的土体，在土体四周施加自由场边界，边界类型为吸收边界(粘性边界)，以考虑自由场阻尼[12]。其中，所述吸收边界为Lysmer和Kuhlemeyer在1969年提出的吸收边界条件[13]：

tn=-ρCpvn

(1)

ts=-ρCsvs

(2)

式中：

tn、ts——法向和切向的牵引力；

ρ——质量密度；

Cp、Cs——P波及S波的速度；

vn、vs——边界法向和切向的速度。

上述吸收边界条件的设置只需在边界类型一项中选中“吸收边界”，软件便可自动进行考虑。整体模型如图5所示。

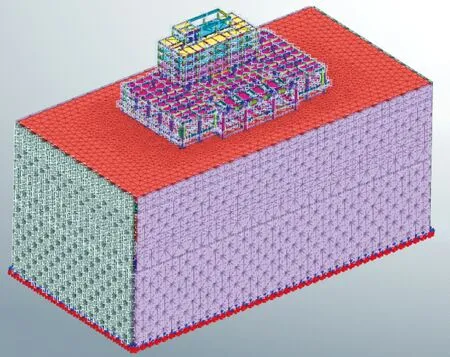
a Midas GTS NX整体模型

在上文所述的建模过程中涉及到了模型从Midas GEN导入到Midas GTS NX模型的过程，为了验证Midas GTS NX导入模型的有效性，需进行上部结构的振型校核。其中，进行模态分析时，恒载转化为质量系数取1.0，活载转化为质量系数取0.5，前3阶主振型校核结果如图6所示，两模型前3阶主振型自振周期差异分别为5.4%、5.0%以及3.1%，满足工程误差要求。

a Midas GEN模型第一阶振型(T1=0.924 s)

3.3 多点激励分析

为了说明问题，在本次多点激励分析中仅以行波效应较为显著的X向进行分析。根据《详勘》报告的剪切波速测试结果，视波速参照剪切波速结果取200 m/s[14]。所有分析中均采用0.02 s时间步长，持续时间30 s。

在Midas GEN模型中，沿模型X方向分14组进行多点激励，激励到达时间根据柱间距除以视波速确定(如图7所示)。在Midas GTS NX模型中，沿模型X方向分42组进行多点激励，激励到达时间根据模型底部土体单元X方向长度除以视波速确定(如图8所示)。

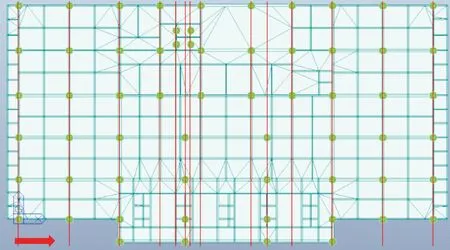
图7 Midas GEN模型多点激励施加示意

图8 Midas GTS NX模型多点激励施加示意

3.4 行波效应分析结果

3.4.1位移分析结果

行波效应位移结果参照点选取塔楼顶点1点，相应位置如图9所示,为了简便说明问题，选取COALINGA-01_NO_364波计算结果进行分析说明。

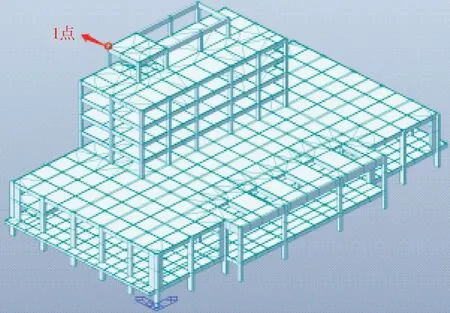
图9 位移结果参考点示意

根据计算结果，CQC法计算的1点X向位移为22 mm，Midas GEN上部结构模型1点X向相对位移计算结果如图10所示，一致激励最大位移为25 mm，多点激励最大位移为20 mm。Midas GTS考虑上部结构与地基相互作用模型1点X向相对位移计算结果如图11所示，一致激励最大位移为28 mm，多点激励最大位移为9 mm。

从图10～图11计算结果可看出以下两个现象：

1) Midas GEN模型相比于Midas GTS NX模型其振动频率更大，且更接近于所施加地震波的震动频率；

2) Midas GTS NX模型中一致激励与多点激励位移结果较Midas GEN模型中一致激励与多点激励位移结果差异大。Midas GTS NX模型中一致激励与多点激励位移结果相差20%，Midas GEN模型中一致激励与多点激励位移结果相差68%，两者相差48%。

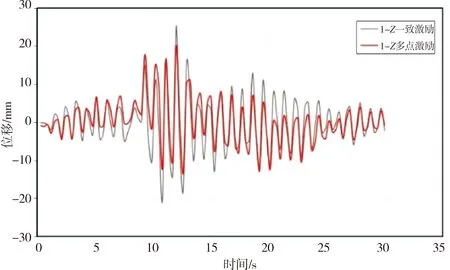
图10 Midas GEN模型1点X向相对位移计算结果示意

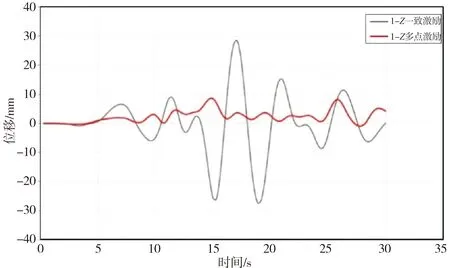
图11 Midas GTS NX模型1点X向相对位移计算结果示意

为了研究差异存在的原因，取上述4个位移分析结果最大时刻X向相对变形进行观察，Midas GEN模型一致激励和多点激励1点X向相对位移最大时刻整体变形如图12所示，Midas GTS NX模型一致激励和多点激励1点X向相对位移最大时刻整体变形如图13所示。

a 一致激励

a 一致激励

从图12a与图12b的对比可以看出，在Midas GEN模型中，多点激励与一致激励相比，多点激励分析时地震波会在上部结构中产生相干效应，导致多点激励与一致激励产生位移上的差异。从图12a与图13a对比可以看出，在考虑了上部结构与地基相互作用后，位移结果会考虑基础结构、土体与上部结构振型的叠加，地震波在土体与结构中产生相干效应，使得其位移与仅考虑上部结构的结果有所差异，从而解释了第1)点现象。从图13a与图13b的对比可以看出，图13a中结构的位移在同一高度上方向基本一致，而图13b中结构的位移呈基本对称形态，说明地震波在行波过程中，于土体和结构中产生较大的相干效应，使图13b中的位移与图13a中位移相比，差异较大，从而解释了第2)点现象。

3.4.2内力分析结果

为了便于说明问题，采用上部结构柱子剪力及其超载系数，作为内力分析结果，其中所述超载系数计算方法为多点激励柱子剪力除以一致激励柱子剪力，柱子剪力提取结果仍以COALINGA-01_NO_364波计算结果作为分析参考。Midas GEN模型以及Midas GTS NX模型柱子剪力计算结果分别如图14及图15所示。

a 一致激励(Max：211 kN)

a 一致激励(Max：51 kN)

从图14及图15的分析结果来看，考虑上部结构与地基相互作用后，柱子剪力峰值明显减小，一致激励结果减少76%，多点激励结果减少89%，但剪力的分布与只考虑上部结构相比有所差别。所选取7条地震波柱子剪力超载系数平均值计算结果如图16所示，图16所示图例中0.7代表该色块构件超载系数处于0～0.7之间，1.0代表该色块构件超载系数处于0.7～1.0之间，以此类推。

a Midas GEN模型(Max：1.93)

b Midas GTS NX模型(Max：2.99)

图16 超载系数计算结果示意

从图16的超载系数分析结果可以看出，在此项目中，考虑上部结构与地基相互作用后超载系数的峰值及分布情况与只考虑上部结构相比有所差别，考虑相互作用后，超载系数峰值有所上升，上升幅度为55%，且行波效应对大部分构件产生了不利影响，但考虑到考虑上部结构与地基相互作用后构件内力下降明显，故采用只考虑上部结构的做法仍能满足设计要求。

4 结论及建议

通过建立Midas GEN上部结构模型以及Midas GTS NX考虑上部结构与地基相互作用模型并分别进行行波效应分析，主要得出以下两点结论：

1) 考虑上部结构与地基相互作用后，多点激励与一致激励之间的位移差异相比于只考虑上部结构而言有所扩大。在所述分析工程中，其扩大幅度约为48%；

2) 考虑上部结构与地基相互作用后，虽然构件内力峰值有所下降，但其内力分布、超载系数峰值以及超载系数分布相比于只考虑上部结构而言有较大差别。在所述分析工程中，考虑结构与地基相互作用后，柱子剪力峰值下降最大89%，超载系数上升幅度为55%。只考虑上部结构时，大部分构件超载系数处于0.7以下，考虑结构于地基相互作用后，大部分构件超载系数处于2.5～3.0之间。

根据以上两点结论，在进行行波效应分析时，特别是对处于抗震不利场地的建筑，建议根据只考虑上部结构分析和考虑上部结构与地基相互作用分析结果进行包络设计，从而保证薄弱构件不遗漏，确保工程安全性。