Ti-48Al-2Cr-2Nb合金高电位电化学腐蚀系统的稳定性特征

2023-01-12林荣联罗志坚廖翠姣

包装学报 2022年6期

林荣联罗志坚廖翠姣

湖南工业大学机械工程学院湖南株洲 412007

TiAl合金作为一种轻质金属间化合物结构材料，具有机械强度、弹性模量高，高温抗氧化性、抗蠕变性、阻燃性好的特点，是未来高推重比航空发动机低压涡轮叶盘的首选材料[1]。传统机械加工TiAl合金的方法刀具磨损大、加工表面完整性差、加工成本高，是制约TiAl合金广泛应用的主要因素。电解加工具有加工效率高、无刀具磨损等优点，已成为TiAl合金加工的首选方法。但电解加工系统是一个多物理场强耦合的非线性复杂系统，呈现明显的混沌特征，且TiAl合金具有不同溶解特性的γ-TiAl和α2-Ti3Al相，以及复杂的微观组织结构，使TiAl合金的稳定高品质电解加工成为难题。因此，研究TiAl合金电化学腐蚀系统的稳定性具有重要意义。

混沌是电化学反应的常见特征，常用的量化表征参数有关联维数、Lyapunov指数和K熵。夏大海等[2]采用相空间重构和关联维数，研究了Q235低碳钢和304不锈钢在不同溶液中电化学噪声的混沌行为，结果表明相空间重构吸引子的关联维数与腐蚀特征相关，局部腐蚀使关联维数增加，并且点蚀的形核、生长增加了电化学噪声信号的复杂性和不确定性。Men H. 等[3]采用关联维数区分304不锈钢在质量分数为3.5%NaCl溶液中钝化、亚稳态点蚀、点蚀发展和稳定点蚀等不同腐蚀特征。M. G. Mahjani 等[4]发现304不锈钢在FeCl3溶液中电化学噪声信号的关联维数与腐蚀表面的分形维数具有良好的相关性，随着FeCl3浓度的增加，关联维数和分形维数均增加。Chen A. N. 等[5]采用最大Lyapunov指数的大小，量化表征Q235低碳钢分别在Na2SO4和NaCl溶液中干湿循环下形成的点蚀数量，发现Q235低碳钢在湿循环和Na2SO4溶液中生成点蚀多、腐蚀不稳定、Lyapunov指数大。

关联维数侧重表征系统变量个数，不能准确反映混沌系统的不确定性；而Lyapunov指数对系统噪声敏感，噪声对其计算结果影响较大；K熵具有计算稳定、误差小、抗噪声干扰能力强等特点，广泛应用于工程领域[6-8]，但并未见到K熵在电化学腐蚀中的相关研究。本文以Ti-48Al-2Cr-2Nb合金为研究对象，采用K熵定量表征合金不同电位电化学腐蚀系统的稳定性，结合电化学阻抗谱和腐蚀表面形貌分析，探究电化学系统稳定性的演化规律及主要影响因素。

1 电化学实验

1.1 主要实验材料与仪器

1.1.1 实验材料

Ti-48Al-2Cr-2Nb合金，宝鸡钛业股份有限公司；无水乙醇，分析纯，天津市富宇精细化工有限公司；硝酸钠，分析纯，西陇化工股份有限公司。

1.1.2 实验仪器

电化学工作站，SAS SP-150/20A型，法国BioLogic公司；扫描电子显微镜（scanning electron microscope，SEM），ZEISS SIGMA 300型，德国卡尔蔡司公司；金相研磨抛光机，MP-1A型，上海精密量仪有限公司；超声波清洗机，G-100S型，深圳市歌能清洗设备有限公司；电热鼓风干燥箱，1010B型，绍兴市苏珀仪器有限公司。

1.2 实验方法

用线切割的方法，将Ti-48Al-2Cr-2Nb合金铸锭切成大小为5.2 mm×5.2 mm×10 mm的样品。实验前将样品封装在环氧树脂中，一端联接铜线作为工件电极，另一端用不同粒度的碳化硅水性砂纸依次进行粗磨、半精磨、精磨，磨出工作面（裸露面积约0.25 cm2，后续电流均采用各自样品的实际裸露面积修正得到相应的电流密度），接着用去离子水和乙醇超声清洗5 min，并在50 ℃的干燥箱内干燥约2 h，获得洁净表面。

采用电化学工作站和三电极（试样为工件电极、铂电极为对电极，饱和甘汞电极为参比电极）组成的电化学系统对样品进行电化学实验测试。本实验使用的电解液是质量分数为20%的NaNO3溶液，由分析纯加去离子水在恒温25 ℃下配制而成。测试流程[9]如下：

1）Ti-48Al-2Cr-2Nb合金在电解液中浸泡2 h，确保开路电位稳定。

2）在10-2～105Hz频率范围内，以10 mV正弦波为扰动信号测量电化学阻抗谱（electrochemical impedance spectroscopy，EIS）。

3）用计时电流法记录合金腐蚀的电流时间序列，记录时间为30 s，采样间隔为0.006 s。电流经修正后得电流密度，从电流密度曲线末端选取4096个数据点分析电流密度的非线性动力学行为。

4）腐蚀后的样品经充分水洗后，换新电解液重新测量EIS。相同电位的电流密度时间序列的采集工作均采用新样品、新溶液在室温25 ℃下至少重复测试3次。腐蚀后样品经超声波清洗5 min后，在烘箱内烘2 h，用扫描电子显微镜观察其表面形貌。

2 电流密度信号降噪与Kolmogorov熵计算方法

2.1 信号降噪

2.1.1 小波阈值降噪法

小波阈值降噪算法简单，对于非线性信号的降噪具有较好的效果[10]，小波阈值降噪的基本过程是：含噪信号经小波分解得到小波系数d，对小波系数阈值量化处理后进行小波逆变换得到重构信号。选择合适的小波基函数对降噪效果至关重要。依据研究者们对电流信号的降噪经验[11-14]，基于固定阈值规则选取合适的信号阈值，通过软阈值函数对原信号的小波系数d进行量化处理，确定分解层数为5，分别通过db2、db10、sym5、sym7 4种小波基函数对电流密度信号进行降噪处理。

2.1.2 变分模态分解降噪法

变分模态分解（variational mode decomposition，VMD）通过采用非递归的变分模式分解原始信号，将其自适应分解为k个具有特定稀疏性质的本征模态函数（intrinsic mode function，IMF），其详细计算过程可参考相关文献[15]。k值的选取决定了变分模态分解的精度，由原始信号各IMF分量的尺度指数α0确定[16]。当α0大于或等于0.7时（其中0.5为白噪声信号的尺度指数，0.2为置信区间）[17]，此信号视为有效IMF分量；否则，视为无效信号，将其舍弃。最后将各有效IMF分量叠加，得到降噪后的信号。该降噪方法具有较小的端点效应和良好的噪声鲁棒性，能够提升强非线性和高复杂性时间序列的平稳性。

2.1.3 降噪效果评估法

由于电化学溶解过程的电流真实信号难以确定，本研究采用降噪前后信号余差的标准偏差（standard deviation of the residual，Residual-SD）[10]和峰值误差（peak error，PE）[18]评估降噪效果。在确保信号不失真的前提下，Residual-SD越大降噪效果越好，而PE则越小越好。由于降噪后部分失真信号也可能会具有较大的Residual-SD，因而本文同时兼顾Residual-SD和PE的大小，二者计算公式为：

式（1）～（2）中：si、fi分别为降噪后信号和原始含噪信号；N为信号长度。

2.2 Kolmogorov熵

K熵量化了非线性系统随时间演化的状态信息损失率，是度量混沌系统稳定性的重要特征参数之一[19]。当K=0，为线性系统；当0＜K＜+∞，为混沌系统，K越大，系统的稳定性越低；当K=+∞，为随机系统[20]。

对于m维动力学系统，设P(i1,i2,…,im)是X(ζ=τ)，X(ζ=2τ)，…，X(ζ=mτ)分别在特定盒子i1,i2,…,im中的联合分布概率，利用式（1）求得Kolmogorov 熵。

式中：r为给定临界长度；τ为延迟时间。

q阶Renyi熵定义为：

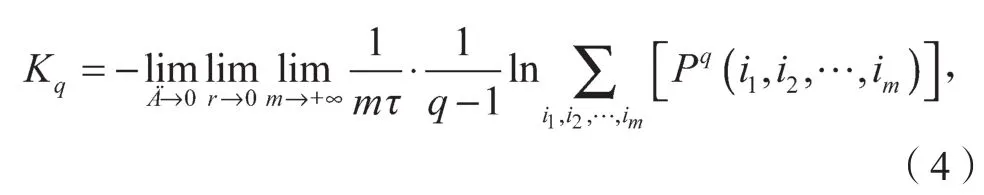
式中：当q=1时，K1为Kolmogorov熵；

当q=2时，K2为二阶Renyi熵。

一般采用K2熵来逼近K熵，可以将K1熵与K2熵在数值上看作相等，K2依次按式（5）～（10）计算获得[21]。

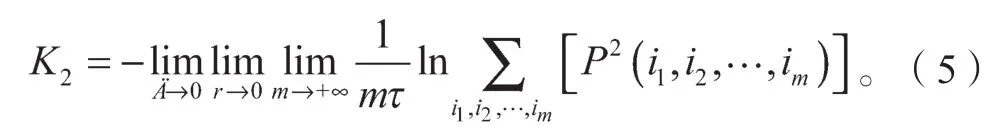
Cm(r)是在m维空间中距离小于r的相位点在所有相位点中所占的比例，表达式为

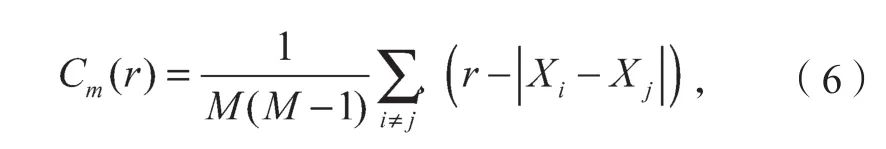
式中：M为总相位点数；

θ(x)为 Heaviside函数

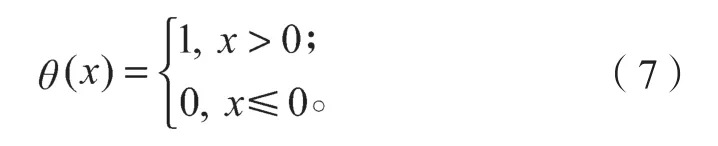
相关积分Cm(r)与X(ζ)的联合分布概率关系为

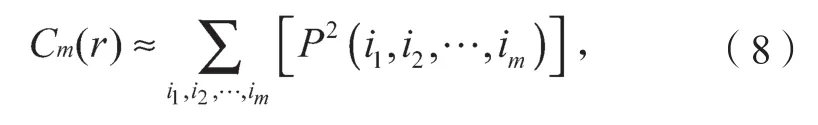
因此

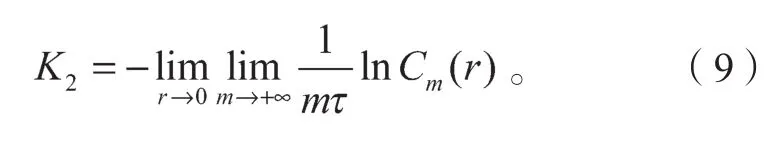
对离散时间序列，时间延迟τ为一常数，则

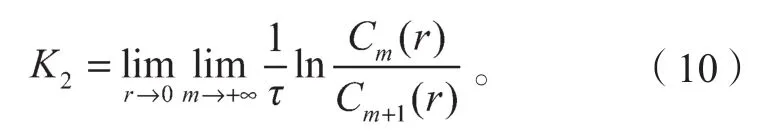
由于式（10）中m→+∞，r→0，在应用中为了简化K熵的计算，取不同计算长度r，分别计算出lnr和lnCm(r)，得到lnr-lnCm(r)双对数曲线。将对数曲线较好的线性区进行最小二乘法拟合，拟合直线在y轴上的截距记为b，此时K熵的计算公式为

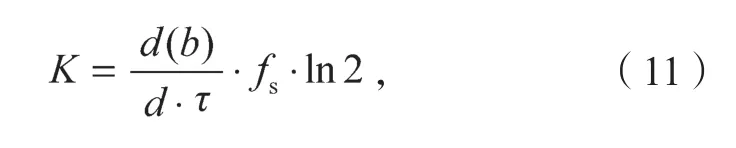
式中：d(b)为截距b的差分；

d为嵌入维数间隔；

fs为采样频率。

3 结果与分析

3.1 电流密度信号降噪效果评估

表1为同一电流密度信号经不同方法降噪后的Residul-SD与PE。由表1可知，4种小波基函数的降噪效果以db2小波基函数最好；而变分模态分解法降噪后的Residul-SD和PE均较大，难以准确判断信号降噪是否彻底、是否失真。因此，本研究根据降噪后电流密度信号的相空间重构吸引子轨迹线的光顺程度，评价降噪效果[22]。

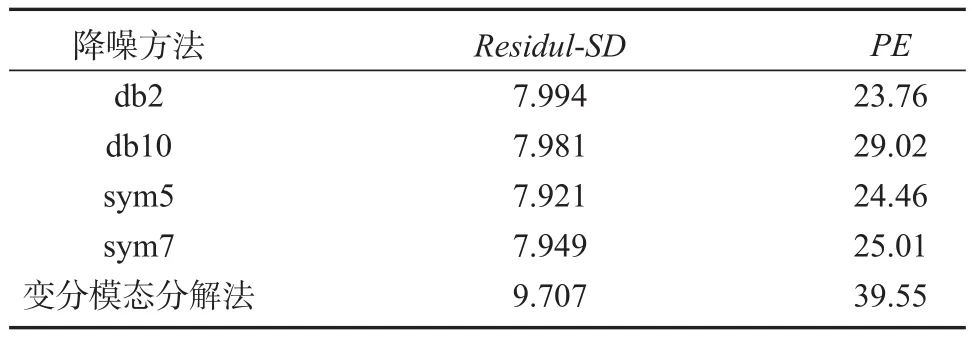
表1 电位为7 V的电流密度降噪后的Residul-SD与PETable 1 Residul-SDand PEafter current density denoising with voltage of 7 V

图1为经不同降噪方法降噪后信号的相空间重构吸引子轨迹线图。由图1可知，原始信号的吸引子轨迹线杂乱且存在许多奇异点，经小波基函数降噪后，重构的吸引子轨迹线的杂乱程度有所改善，但还不够光顺，存在较多奇异点。经变分模态分解降噪后信号重构的吸引子轨迹线，光顺程度改善明显，奇异点少，且保持了原有信号的演变规律，这说明该方法的降噪效果最好。因此，本研究采用变分模态分解法对电流密度进行降噪处理。另外，重构的吸引子轨迹线在相空间平面内呈45°对角线对称分布，可以初步判断Ti-48Al-2Cr-2Nb合金的腐蚀形态以均匀腐蚀为主[23]。

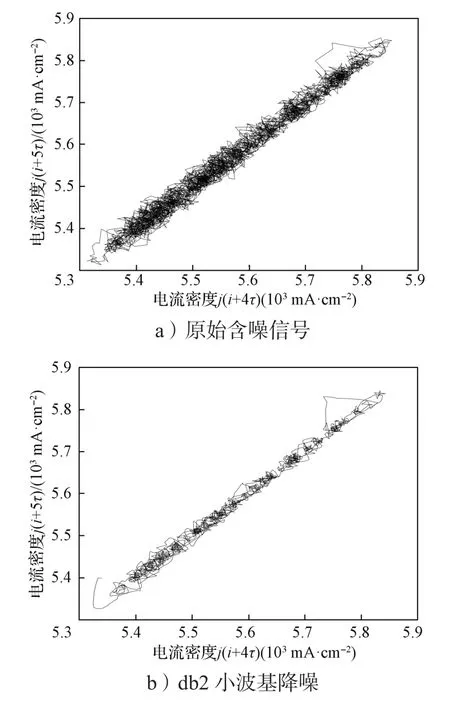
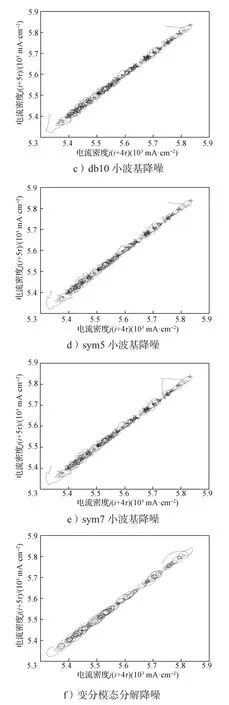
图1 电位为7 V的电流密度降噪前后的相空间重构吸引子轨迹线图Fig. 1 Phase space reconstruction attractor trajectory diagram before and after current density denoising with voltage of 7 V

图2为不同腐蚀电位下Ti-48Al-2Cr-2Nb合金的电流密度曲线。由图2a可知，在腐蚀前期电流密度波动均较大，随着腐蚀时间的延长，波动逐渐变小并趋于稳定，这归因于合金在腐蚀过程中腐蚀形态的转变。腐蚀前期以局部腐蚀为主，腐蚀后期逐渐以均匀腐蚀为主。电流密度在腐蚀后期有下降的趋势，主要有3个原因：随着腐蚀时间的延长，1）腐蚀产物增多，吸附产物在表面吸附量增大；2）两电极间生成的气泡量增大；3）两电极的间距稍有增大。这些原因增大了两电极间的电阻，使电流密度降低。

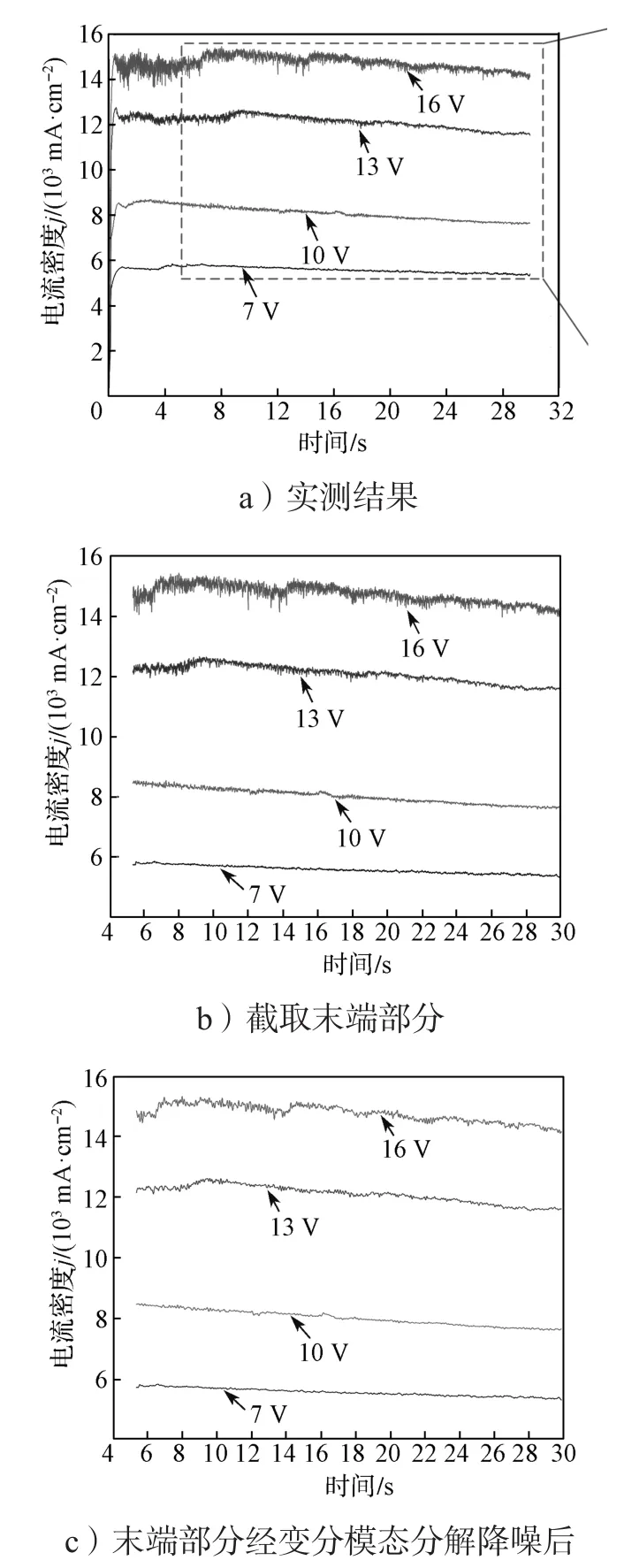
图2 不同腐蚀电位下Ti-48Al-2Cr-2Nb合金的电流密度曲线Fig. 2 Current density curves of Ti-48Al-2Cr-2Nb alloy at different corrosion potentials

将电流密度曲线末端（图2b）截取的数据，采用变分模态分解法降噪。从降噪后的信号（图2c）可以看出，降燥后的信号有效保留了信号的真实性，同时具有较好的平滑度。

3.2 电位对电化学系统稳定性的影响

不同嵌入维数下，电化学系统的lnr-lnCm(r)双对数曲线如图3所示。由图3a可知，随着lnr增加，lnCm(r)逐渐收敛；随着嵌入维数m的增加，线性拟合区域的斜率逐渐稳定。由图3b可知，曲线的拟合程度好，拟合精度达到0.9997以上。

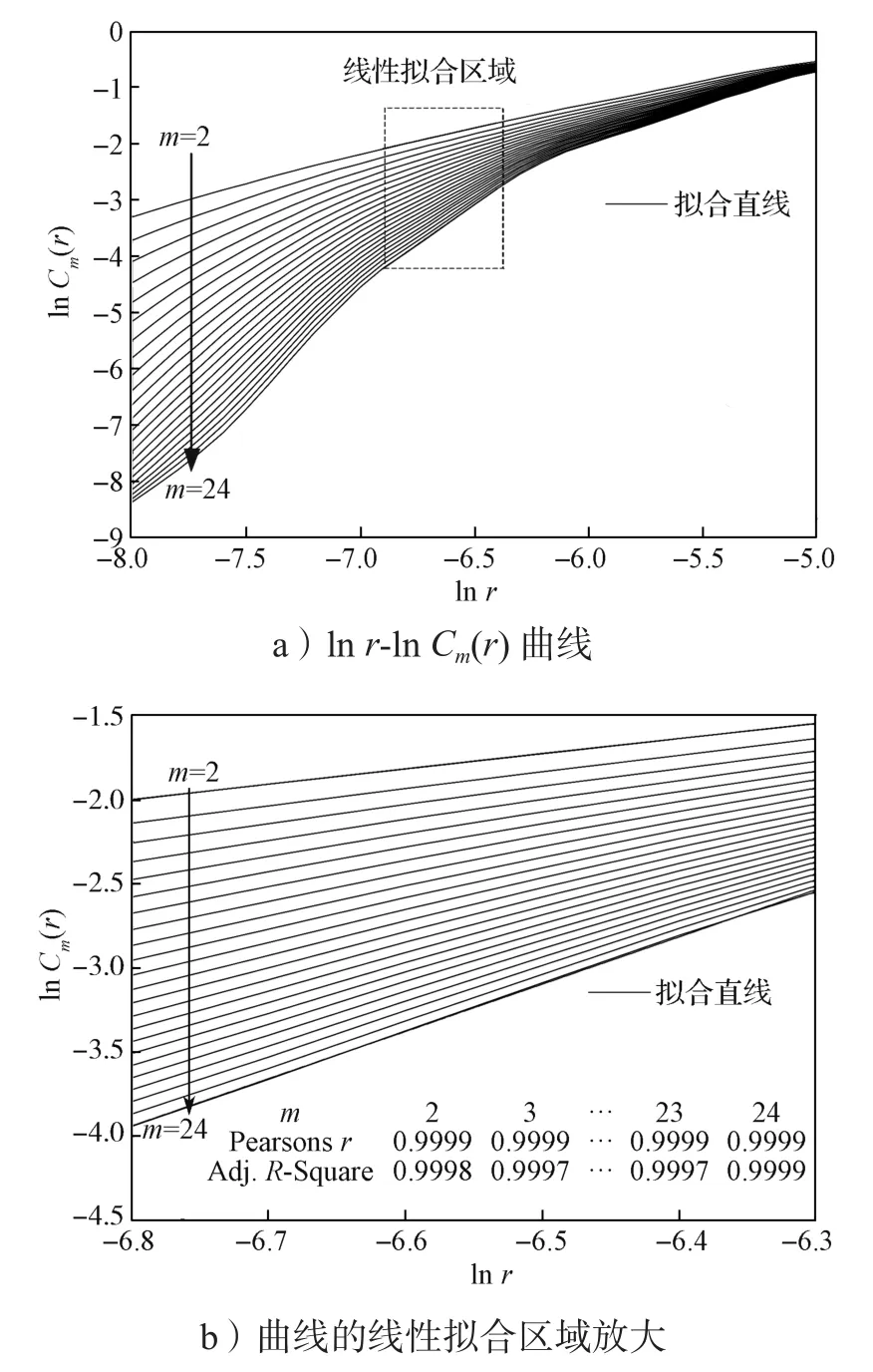
图3 ln r-ln Cm(r)曲线及线性拟合Fig. 3 ln r-ln Cm(r) curves and linear fitting

图4为不同电位下电化学系统的K熵随嵌入维数m的变化曲线。由图4可知，随着m的增加，K熵下降，最后收敛于某一稳定值，此值为该系统的K熵，各具体数据见表2。

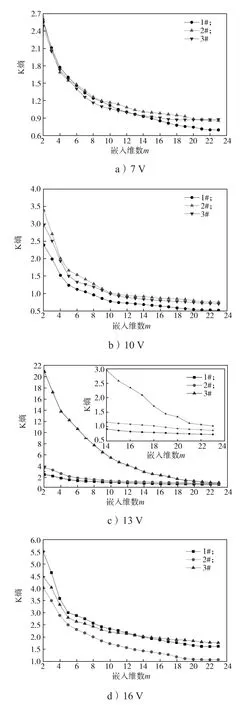
图4 不同电位的K熵与嵌入维数m的关系Fig. 4 The relation between K entropy of different potentials and embedding dimension m

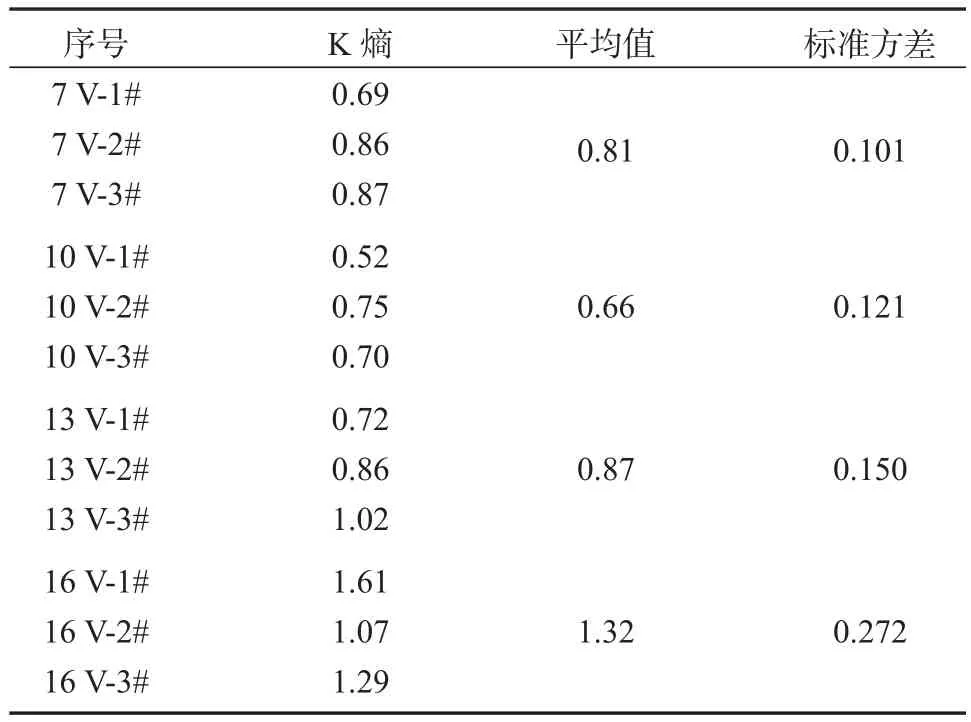
表2 不同腐蚀电位下电流密度的K熵Table 2 K entropy of current density at different corrosion potentials

由表2可知，不同电位的电流密度时间序列的K熵均大于零，且有一定的差异，说明电化学腐蚀系统在实验电位范围之内均呈现明显的混沌特性，且受电位影响。

图5为K熵与腐蚀电位的关系曲线。从图5可知，电位从7 V增加到10 V时，K熵缓慢下降；从10 V增加到13 V时，K熵缓慢上升；从13 V增加到16 V时，K熵快速上升。这表明电化学腐蚀系统的稳定性随电位增加先升高后降低，且稳定性变化幅度增大。电位为7 V～13 V时，K熵的标准偏差较小；电位为16 V时，K熵的标准偏差较大，也说明了16 V时系统的稳定性低。引起这些差异的原因是电位增大，电流密度增加，反应程度更剧烈，生成的絮状腐蚀产物增多、气泡数量急剧增加，在电极表面形成多个局部气泡层[24]。多因素强耦合作用加剧了系统复杂程度，降低了系统稳定性。

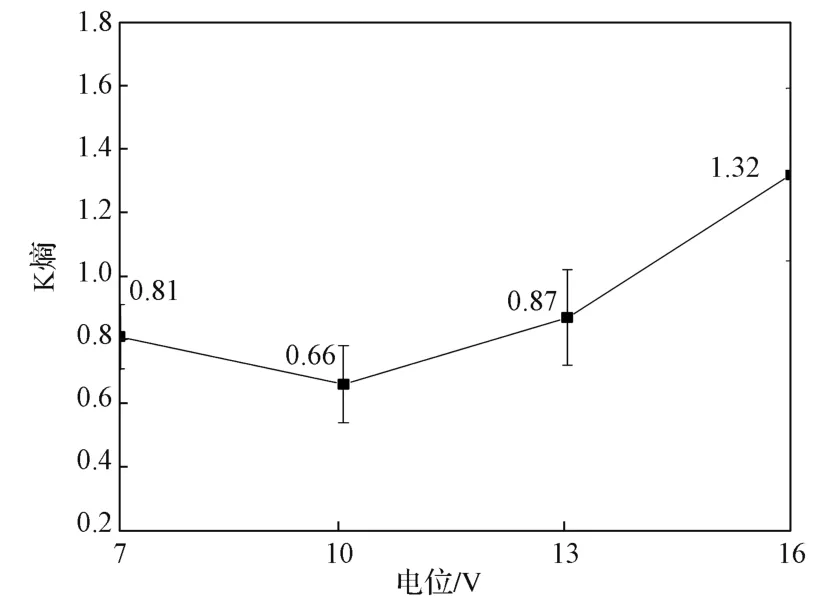
图5 K熵与腐蚀电位的关系曲线Fig. 5 Relation between K entropy and corrosion potential

3.3 电极界面结构分析

采用电化学阻抗谱分析Ti-48Al-2Cr-2Nb合金电极腐蚀前后界面结构的变化[25]，结果如图6所示。

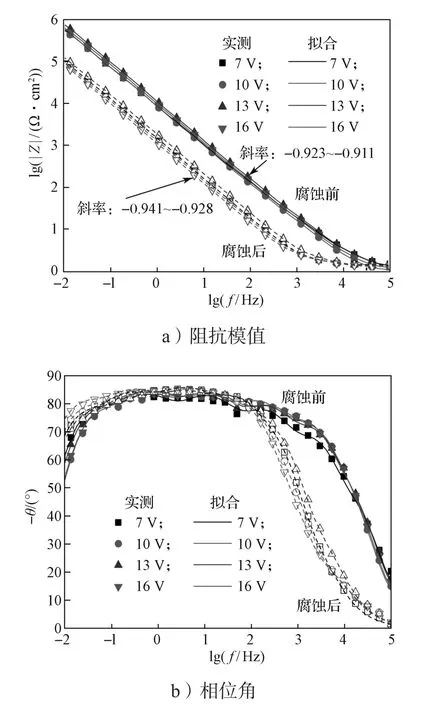
图6 Ti-48Al-2Cr-2Nb合金不同电位腐蚀前后实测和拟合阻抗谱Bode图Fig. 6 Bode plots of impedance spectra of Ti-48Al-2Cr-2Nb alloy measured and fitted before and after different potential corrosion

图6a中的实测阻抗模值表明：合金在腐蚀前阻抗模值从高频到低频先出现一个短暂的平台区后迅速增加，最大值达到106Ω·cm2，这与合金表面的高耐蚀性能有关。合金经腐蚀后，阻抗模值在高频区为一个平台，表现为溶液电阻，在中低频区随着频率下降迅速增加，最大值接近105Ω·cm2，合金抗腐蚀能力明显下降。此外，腐蚀后阻抗模值直线部分斜率的绝对值增大，更接近于1，界面结构发生较大改变。从图6b（散点图）可以看出：在高频区，腐蚀前相位角随频率减小快速增大，腐蚀后则先缓慢增大后快速增大，且腐蚀前的相位角大于腐蚀后的。在中频区，腐蚀前相位角有小波动，腐蚀后相位角较平稳且稍有增加，腐蚀后比较平滑，最大相位角接近-85°。在低频区，腐蚀前相位角随频率降低快速下降，腐蚀后则缓慢下降，最终前者相位角小于后者。经EIS分析表明，合金经过腐蚀后样品的抗腐蚀能力下降，且明显改变了电极界面结构。

为了更准确量化表征合金腐蚀前后界面结构的变化，在Zview软件中采用Maxwell 传输线等效电路模型[22]（图7）对阻抗谱进行拟合，拟合曲线如图6所示，参数拟合结果如表3所示。

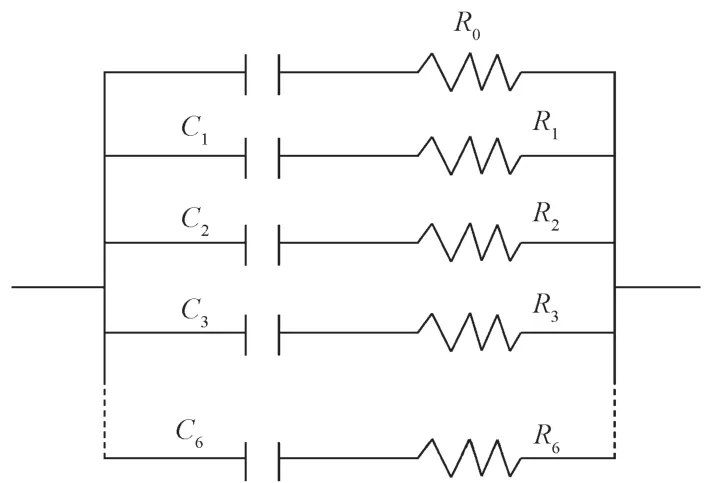
图7 阻抗谱拟合等效电路模型Fig. 7 Impedance spectrum fitting equivalent circuit model

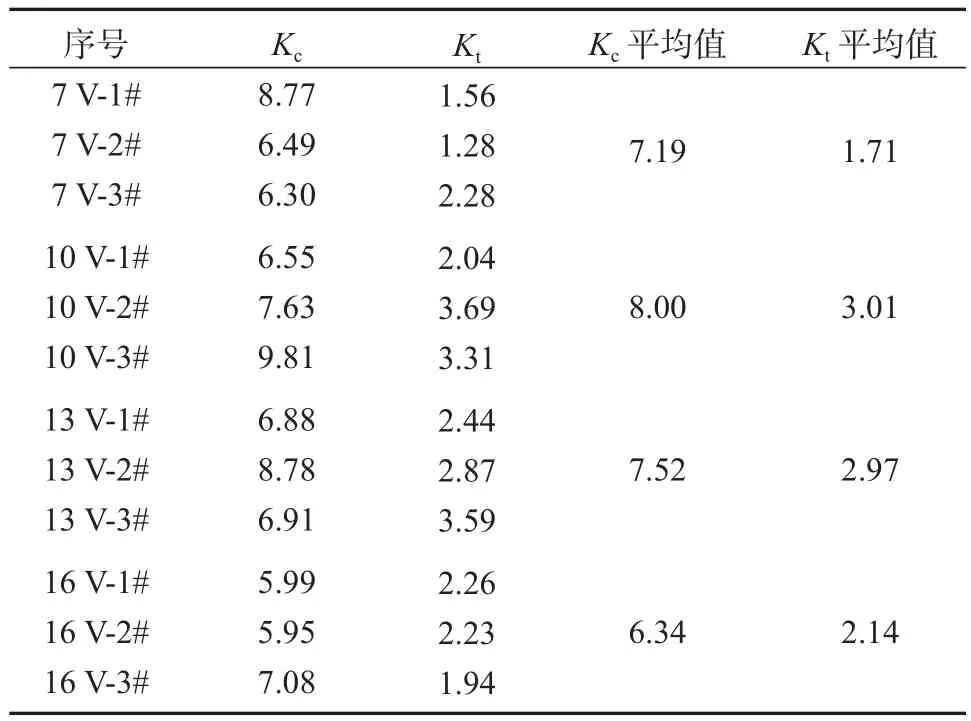
表3 Ti-48Al-2Cr-2Nb合金腐蚀前后阻抗谱拟合参数Table 3 Impedance spectrum fitting parameters of Ti-48Al-2Cr-2Nb alloy before and after corrosion

图7中，R0为极化电阻，Ri、Ci（i=1, 2, …, 6）分别为中间腐蚀产物吸附反应的电阻和电容。总电容表征电极表面粗糙程度，数值越大表示粗糙程度越高；时间常数表示吸附反应响应速度快慢，其值越大表示响应速度越慢[26]。对于同一电极，腐蚀前后总电容比Kc=C后/C前表示合金腐蚀前后粗糙程度的变化，即电极界面粗化程度，当Kc大于1时，表示表面变粗糙。腐蚀前后总时间常数比Kt=t后/t前表示界面吸附反应响应速度的变化，当Kt大于1时，表示响应速度变慢。由表3可知，合金经腐蚀后表面变粗糙且吸附反应响应速度变慢。

3.4 电极界面粗化程度和吸附反应的响应速度对电化学系统稳定性影响

图8为不同电位电化学腐蚀系统K熵与腐蚀前后总电容比Kc的分布图。由图8可知，不同电位时Kc对系统稳定性影响程度不同：当电位为7, 10, 13 V时，Kc分别为 6.30～8.77、6.55～9.81，6.88～8.78，每种电位下Kc的分布范围大，对应电化学系统K熵的变化较小，表明此时电化学系统稳定性受电极粗化程度影响不显著；当电位为16 V时，Kc为5.99～7.08，Kc分布范围小，对应电化学系统K熵的变化较大，表明在高电位下，电化学系统稳定性受电极腐蚀后界面粗化程度影响显著。

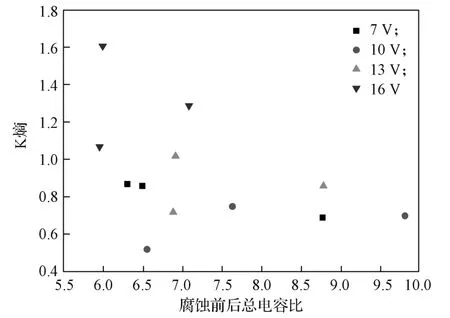
图8 K熵与腐蚀前后总电容比Kc的关系Fig. 8 Relation between K entropy and capacitance ratio Kc before and after corrosion

图9为不同电位下K熵和腐蚀前后总时间常数比Kt的分布图，其反映了电极吸附反应响应速度对电化学腐蚀系统稳定性的影响程度。由图9可知，Kt对不同电位下电化学腐蚀系统稳定性的影响程度不同：当电位为7, 10, 13 V时，Kt分别为1.28～2.28、2.04～3.69和2.44～3.59，每种电位下Kt分布范围较广，而K熵的变化范围小，说明Kt对系统稳定性的影响不显著，即吸附反应响应速度对系统稳定性影响不显著；当电位为16 V时，Kt为1.94～2.26，变化范围最小，但K熵的变化非常显著，表明吸附反应响应速度对电化学系统稳定性的影响显著。

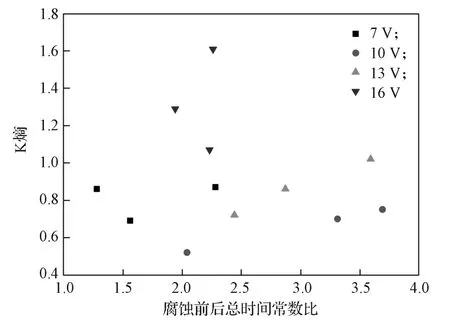
图9 K熵与腐蚀前后总时间常数比Kt的关系Fig. 9 Relation between K entropy and time constant ratio Kt before and after corrosion

3.5 合金表面形貌分析

图10为Ti-48Al-2Cr-2Nb合金在不同电位下腐蚀后表面形貌扫描电镜图。由图10可知，合金经不同电位腐蚀后表面均呈现出片层腐蚀、点蚀和晶界腐蚀特征，具体腐蚀形态与合金的微观组织和外加电位密切相关。平行电极表面的片层均有点蚀特征（图10中的白色箭头所示处），与外加电位的高低无关。

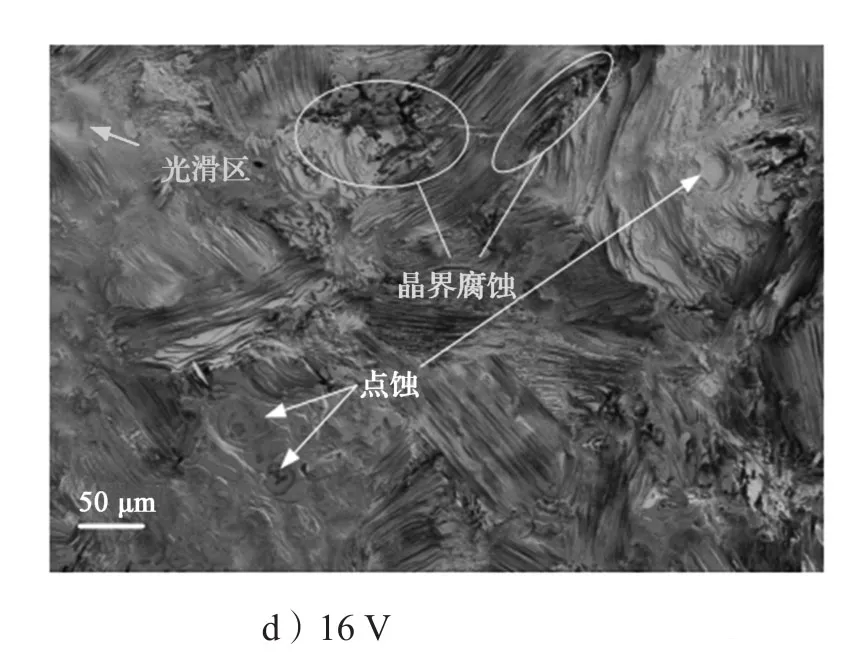
图10 不同电位下Ti-48Al-2Cr-2Nb合金经腐蚀后表面形貌Fig. 10 Surface morphology of Ti-48Al-2Cr-2Nb alloy after different potential corrosion

彩图

合金在7 V电位下腐蚀后，表面有少数离散光滑而平整的小区域（图10a中的红色箭头所示处），是由腐蚀前期局部腐蚀演化形成，此特征在其他电位均未出现。合金在晶界处发生明显腐蚀，且随着电位的升高，晶界腐蚀深度先加深后变浅，其中以10 V的晶界腐蚀最深（图10中黄色椭圆标示处）。Ti-48Al-2Cr-2Nb合金中γ-TiAl和α2-Ti3Al相的溶解速度差异，随着电位的升高逐渐减小，故合金在16 V电位下腐蚀后表面平整度最好。

从Kc的大小可知，当外加电位为7～10 V时，电极表面随电位升高而明显变粗糙，当电位为10～16 V时，电极表面随电位升高粗糙程度有所降低，经16 V电位下腐蚀后的样品表面最光滑，这一变化规律与扫描电镜照片显示的结果基本相符。合金表面变平整的主要原因是高电位腐蚀反应剧烈，合金中的γ-TiAl相和α2-Ti3Al的溶解速度差异逐渐变小，优先腐蚀不明显，片层结构以均匀腐蚀为主。此外，生成的大量气泡在破裂过程中由于破裂的急剧冲击作用，也有可能使表面变得光滑，如图10c和10d中橙色箭头所示处。

结合K熵可知，当腐蚀电位为7 V时，合金发生点蚀，点蚀的形核、长大和发展增加了电流密度的复杂性和不确定性，使电化学系统的稳定性降低；当腐蚀电位为10 V时，腐蚀形态以片层的选择腐蚀和晶界腐蚀为主，电化学系统稳定性稍有增强；后续随着电位的升高，虽然表面逐渐变平整，但反应越来越剧烈，生成的腐蚀产物和大量的气泡，使系统稳定性变差。