再入飞行器中制导段微分对策式主动机动方法研究
2023-01-12赵亮博朱广生
赵亮博,徐 玮,朱广生,陈 旸,庄 凌,
(1. 北京航天长征飞行器研究所,北京,100076;2. 火箭军重大专项中心,北京,100096; 3. 中国运载火箭技术研究院,北京,100076)
0 引 言
再入飞行器的机动策略问题,一直是再入飞行器制导控制领域的研究热点[1]。同时,随着防御一方技术水平的不断提高,对进攻方的机动策略也提出了更高的要求[2]。飞行器主动机动过程具有非线性、时变性和不确定性等特点,其制导策略除了需要满足各项飞行约束外,还需要能够针对拦截器的飞行信息实时做出有效的机动动作,并形成有利的飞行态势。
现今,再入飞行器机动形式主要有程序式机动和主动式机动两类[3]。程序式机动包括正弦机动、方波机动等平面机动,以及螺旋机动等各种复杂空间机动。此类机动方法不考虑攻防对抗双方的相对运动关系,一般按提前装订的飞行规律实施规避机动。
随着飞行器性能的不断提升,主动式机动策略由于具有更好的规避效果逐渐受到人们重视。此种方法源于制导系统设计中的最坏目标机动问题和飞机机动中的追踪逃逸问题[4]。最坏目标机动问题最早由Shinar提出,并用最优控制的方法加以解决:对象对运动线性化得到了脱靶量的解析表达式。同时,他给出一种Bang-Bang控制的最优机动策略,一方在相遇过程中不断变换自己横向加速度符号,变换的周期与拦截器的比例导引系数有关。与最坏目标机动相比,追踪逃逸问题基于双方均可以获得当前相对运动信息的情况下,研究对自己最为有利的机动策略,在体现对抗性方面具有独特的优势,且在模型上不需要做过多的简化。
微分对策理论最早由Isaacs提出[5],美国科学家Fridman于1971年严格证明了微分对策值与鞍点的存在形式[6],从而奠定了微分对策坚实的理论基础。随着微分对策理论日趋成熟,其应用范围也逐步扩大。Jarmark等考虑飞机的机动能力限制,采用微分对策理论解决空战双方对抗问题[7]。张秋华在此背景下,以轨道数量为状态变量,在双方均为径向连续可变小推力的假设条件下,研究推导出可变推力的最优控制量[8]。王雨琪[9]等针对飞行器设计了微分对策制导律,对比例导引拦截器实现了有效机动,但是未考虑飞行器的动力学特性。
一方面微分对策数值解对计算能力要求高,难以实现在线应用,另一方面随着传感技术的发展实时获取双方位姿信息逐渐变得可能,研究基于实时信息的机动反拦截策略逐渐变得具有实际意义。因此本研究针对再入飞行器滑翔中制导段的主动机动策略,设计了一种基于微分对策解析解的主动机动反拦截制导方法。在对相对运动建模分析的基础上,以能量消耗和相对距离为基础构建性能指标,求解微分对策的解析解,并针对一阶惯性环节特性的比例导引拦截器,设计博弈场景进行仿真校验。将所设计制导方法通过与无机动、正弦机动等形式进行对比分析,检验该算法的有效性,为该算法的工程应用奠定理论基础。
1 问题描述与建模
1.1 主动机动场景描述
随着精确探测制导技术的发展,不仅是防御一方的能力得到了迅速提升,进攻方对拦截器的实时探测也逐渐变得可能。主动式机动策略就是在进攻飞行器已被敌方发现,且拦截一方已经实施拦截时,进攻方可以根据探测到的双方相对运动信息,进行实时的博弈机动,并最终实现反拦截的目的。
本研究中涉及的交战场景是再入飞行器在滑翔中制导飞行段,探测到有敌方拦截器的抵近,再入飞行器为了规避拦截进行了相应的反拦截机动。拦截器采用逆轨前置拦截法,制导律为比例导引,具体飞行参数见仿真校验章节。同时,为了求得基于微分对策解析解的机动制导策略,本研究进行了以下合理假设:
a)拦截方为采用比例导引拦截器的质点模型,自带驾驶仪近似为一阶惯性环节;
b)攻防对抗双方均能够准确获得对方的位置、速度信息,不考虑状态估计误差。
1.2 飞行器与拦截器数学模型
本文研究的飞行器采用无动力平衡滑翔的方式再入,对中制导段的机动反拦截制导策略进行设计。为描述飞行器运动,忽略地球曲率和自转的情况下建立飞行器的运动方程如下:
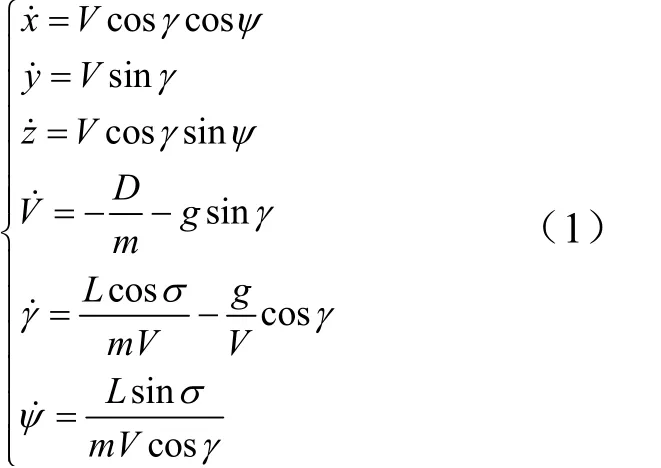
式中 (x,y ,z)为飞行器在惯性坐标系中的位置;V为飞行器速度;(γ ,ψ ,σ)分别为航迹倾角、航迹偏角和倾侧角;g为重力加速度;m为飞行器质量;L,D分别为升力和阻力,具体表达式如下:

式中 ρ为大气密度;refS为参考面积;LC,DC分别为升力和阻力系数,为马赫数Ma和攻角α的函数。
拦截器视为惯性空间中的质点,其法向过载的响应特性近似为一阶惯性环节,形式如下:

式中 τ为时间常数;a为实际过载;ca为过载指令。此外,在整个飞行过程中认为拦截器轴向不具有加速度能力。
1.3 相对运动关系建模
为描述攻防对抗双方的相对运动关系,便于微分对策理论的推导,建立相对运动模型,如图1所示。
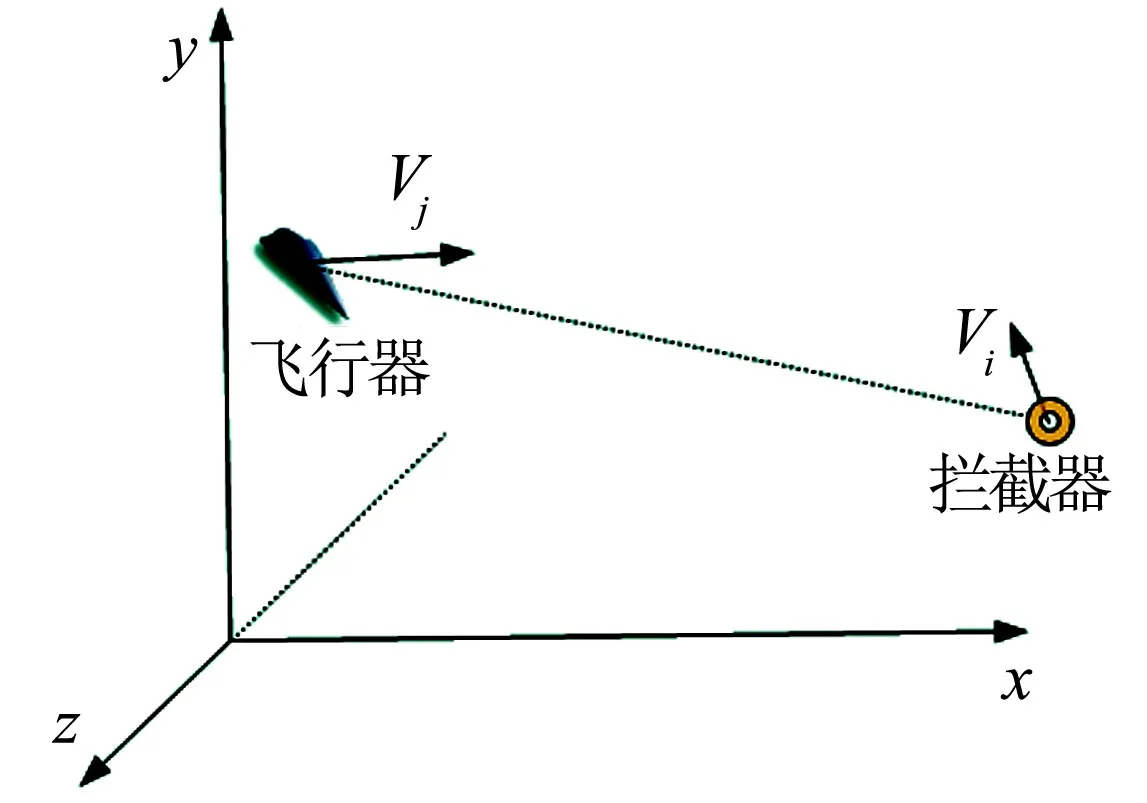
图1 飞行器与拦截器相对运动关系 Fig.1 Relative Motion between Vehicle and Interceptor
在惯性坐标系下描述相对运动关系为
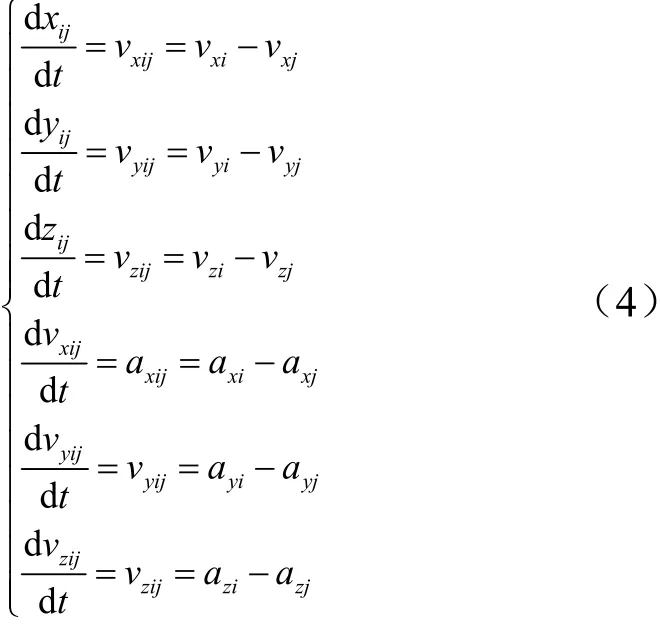
式中 (xj,yj,zj),(vxj,vyj,vzj),(axj,ayj,azj)分别为飞行器的位置、速度、加速度,变量j相关状态为飞行器状态; (xi,yi,zi),(vxi,vyi,vzi),(axi,ayi,azi)分别为拦截器的位置、速度和加速度;(xij,yij,zij),(vxij,vyij,vzij),(axij,ayij,azij)分别为飞行器和拦截器的相对位置、相对速度和相对加速度。
此时,选取:状态变量 X =[xij,vij],控制变量ui=[axi, ,ayi,azi]T,uj=[axj,,ayj,azj]T。则可以改写为如下形式:
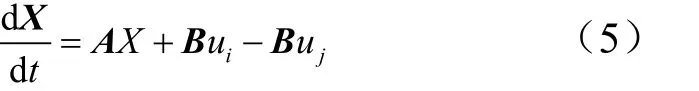
此种形式的微分方程,便于微分对策制导律解析解的推导。
2 微分对策制导策略
2.1 微分对策性能指标的构建
本研究中将飞行器与拦截器的攻防博弈问题视为两方零和博弈问题进行求解,即在攻防对抗的过程中飞行器要摆脱拦截器的追击,使自己尽可能的远离拦截器,而拦截器一方则尽可能的靠近飞行器。此时,飞行器一方的收益增量即为拦截器一方的损失量,反之亦然。此外,在博弈的过程中还应考虑能量的消耗,即尽可能使己方的能量消耗小,而使对方的能量消耗大。在中制导阶段,影响最终拦截成败的主因是双方的加速度,相对位置和相对速度影响较小,因此设计性能指标为Lagrange型与Mayer型的复合。综上,建立性能指标形式如下:

对于两方零和博弈问题,若式(6)中的Q和R矩阵满足非负定与正定要求,那么存在一鞍点。在该鞍点 (下,飞行器的控制策略uj和拦截器的控制策略iu,对于一切的控制策略,都有:
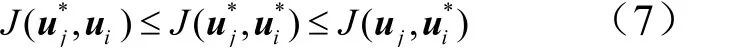
2.2 微分对策问题的解析解
为求解鞍点,结合式(6)构造哈密顿函数:
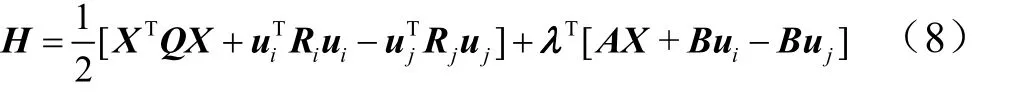
式中 λ ∈ R6为协态向量。此时,求解minH (…)的必要条件,即鞍点条件为

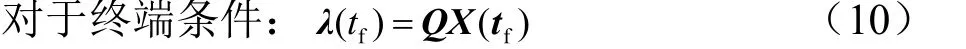
对应的充分条件为

将必要条件代入哈密顿函数可得:
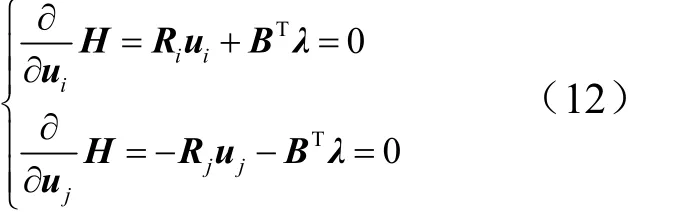
根据式(10)、式(11)可得:

制导指令是与系统状态相关的函数,在没有干扰项的情况下可以将λ假设为如下形式:
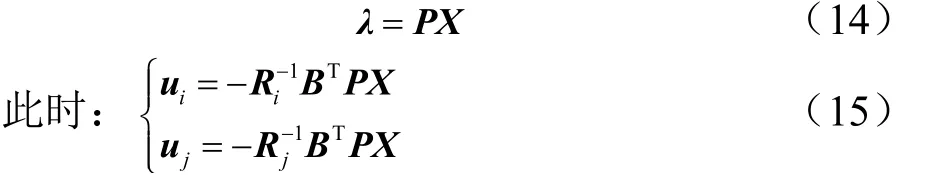
式中 Ri-1BTP为飞行器反馈增益; R-
j
1BTP为拦截器反馈增益。由必要条件式(9)和哈密顿函数式(8),并代入状态方程可得:
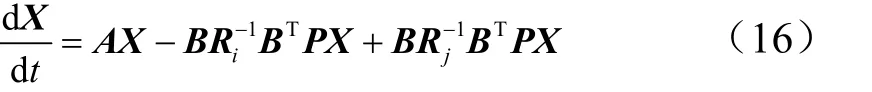
结合式(16):
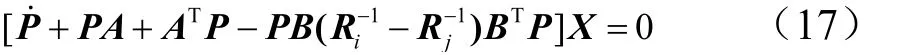
由于式(17)的解必须满足所有的状态X,因此得到矩阵黎卡提微分方程:

一般情况下,式(17)代表的矩阵黎卡提方程很难直接获得解析解。而数值类解法大多数情况下计算效率低,难以实现飞行器在线应用。因此是否能够获得计算效率更高的解析解,是基于微分对策的制导律能否实际应用的关键。为此,在忽略制导律性能次要影响因素的情况下,对整个过程涉及的变量进行适当形式的化简,最终得到适用的解析解,其中简化包括:
a)忽略中制导阶段各个方向上状态的相互耦合,即只保留矩阵Q中的对角项;
b)飞行器做无动力飞行,轴向不做机动动作,横侧向机动过载可解耦;
c)拦截器也具有三自由度解耦的机动能力。
因此代表加速度性能的矩阵 iR和 jR可以化简为只有对角项的矩阵形式。此时:
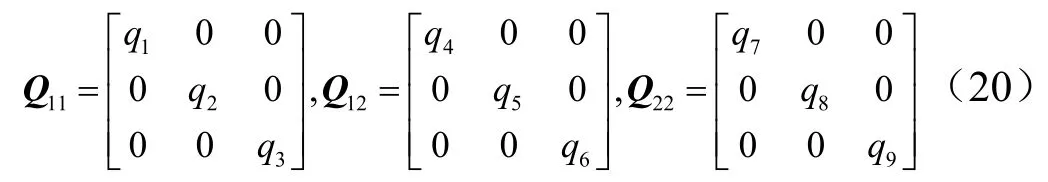
式中 qi(i= 1,2,…,9)代表了末端状态的权重,根据不同的需求可以设置不同的参数。
求解矩阵黎卡提微分方程涉及逆矩阵,即首先求解矩阵黎卡提微分方程逆矩阵的解,然后将得到的解进行求逆,最终得到黎卡提矩阵。
定义剩余飞行时间 T=tf-t,此时,设置 权 重 参 数: q1=q2=q3=q1′, q4=q5=q6= q2′,,而且r1=r2=r3=r。
对于矩阵P的详细推导过程见参考文献[10],在此不做赘述。最终得到矩阵黎卡提方程的解:
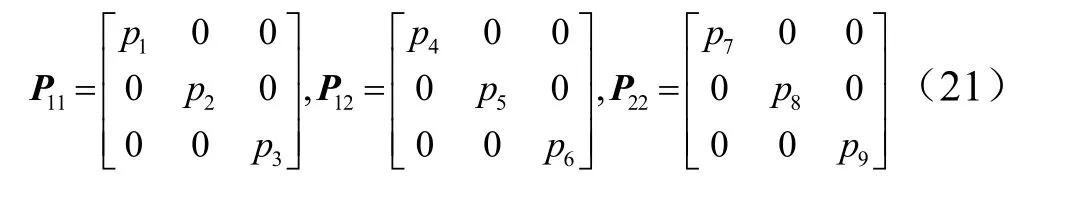
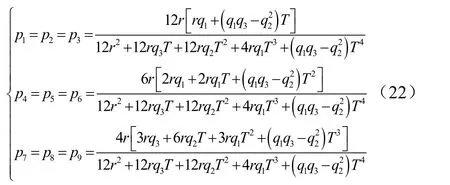
将该解代入式(15)可以得到基于微分对策解析解的机动制导算法。在该制导指令的基础上,将惯性系下的过载指令转换至弹体系下[11],并通过气动系数的反插值可以求得攻角指令cα、倾侧角指令cσ:
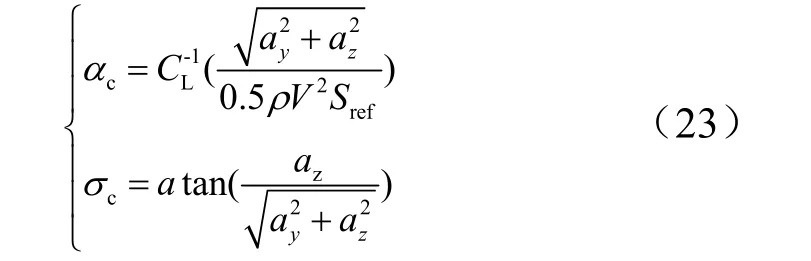
式中ya,za分别为弹体系下的y向和z向加速度指令。
3 仿真校验及分析
3.1 仿真条件
本研究中采用CAV-H的数学模型行仿真验证[12],根据工程经验,在惯性系中飞行器的y向和z向加速度限定在2.2g以内。微分对策制导律参数设置中:Rj= 0.0008I 。表1为飞行器的初始点参数设计.
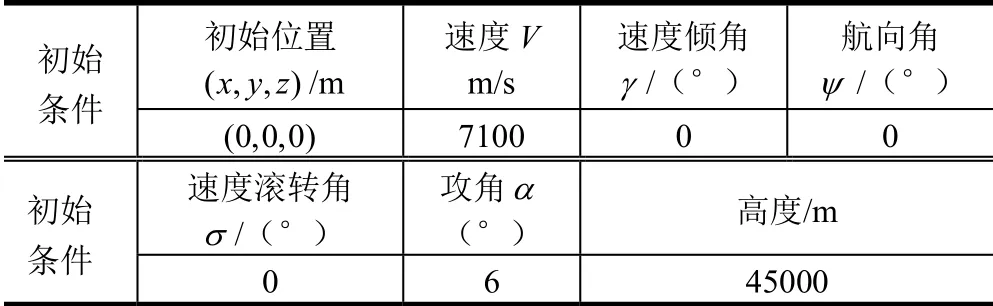
表1 飞行器初始点参数 Tab.1 Vehicle Initial Point Parameters
针对特殊飞行环境,拦截器的各项性能均受到不同程度的限制,考虑拦截器的自动驾驶仪为一阶惯性环节,时间常数为0.5 s,25 km高度以上时最大可用过载为6g。拦截器采用逆轨前置拦截法,制导律为比例导引制导律,导引比为4。仿真初始条件设置见表2。

表2 拦截器初始点参数 Tab.2 Interceptor Initial Point Parameters
3.2 对比分析
分别在飞行器不进行机动、采用正弦机动以及微分对策机动3种情况下,进行机动能力的对比仿真。其中飞行器做正弦摆动式机动时,加速度指令形式为
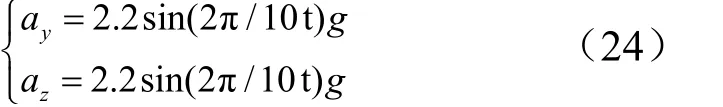
飞行器和拦截器飞行轨迹如图2~4所示,无机动以及正弦机动情况下,拦截器脱靶量均在20 m以内。采用微分对策制导律时,飞行器为了躲避拦截器首先进行了偏下和偏右的空间机动,这与探测到的拦截器起始位置和速度有关。飞行器虽然进行了有效的机动,造成了149.07 m的脱靶量,但是飞行器过程中飞行高度变化较大,见表3。

表3 不同机动形式对比 Tab.3 Comparison of Results of Different Maneuver Forms
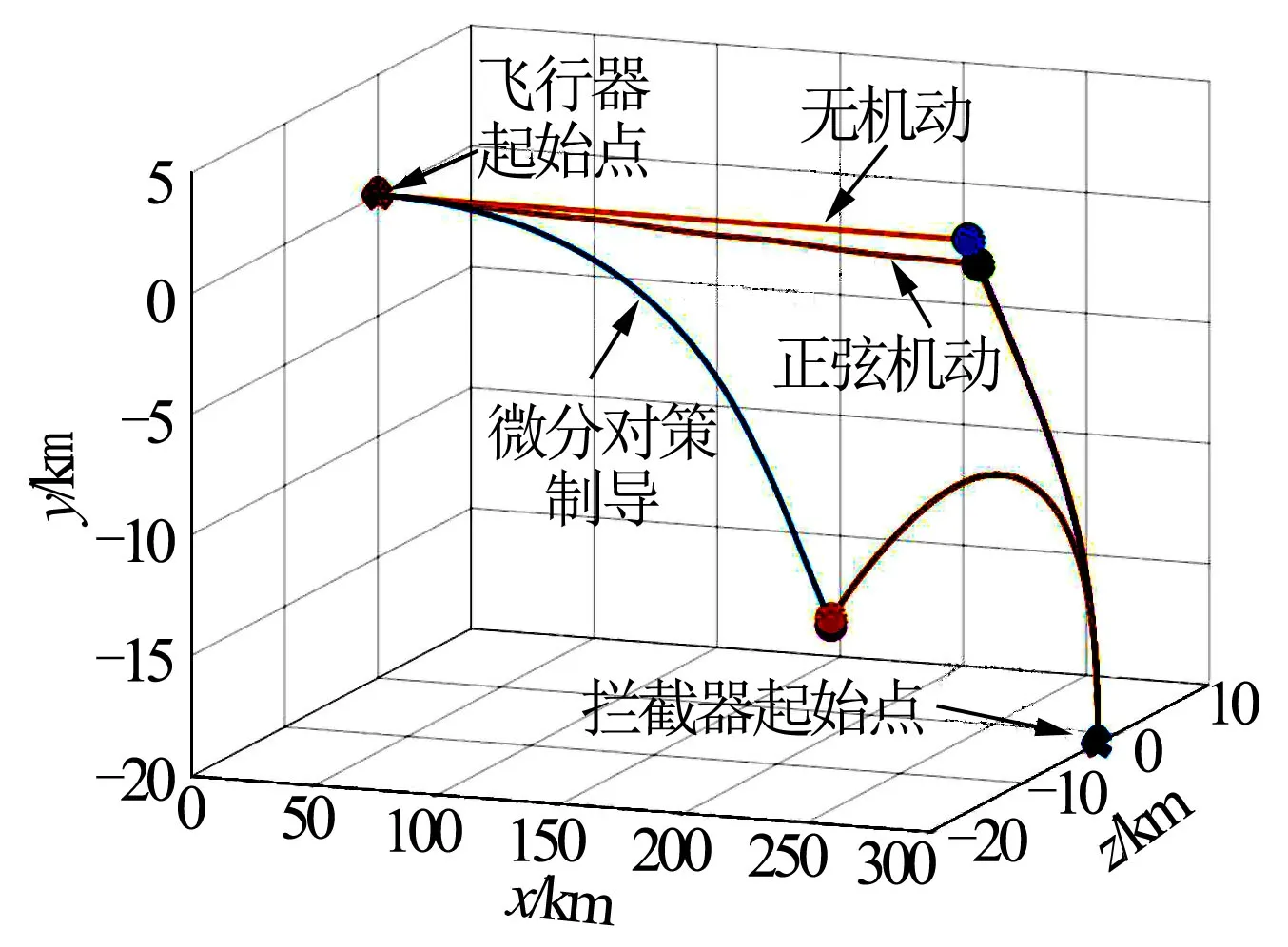
图2 三维飞行轨迹 Fig.2 3D Flight Path
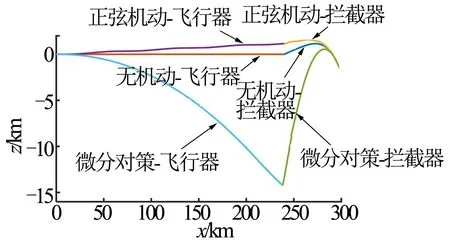
图3 x-z平面轨迹 Fig.3 x-z Plane Flight Path
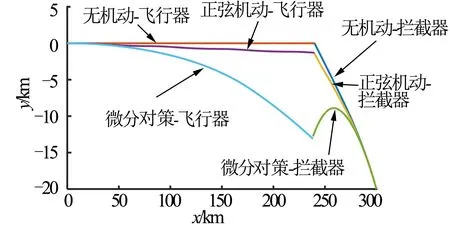
图4 x-y平面轨迹 Fig.4 x-y Plane Flight Path
飞行器过载以及对应的攻角和倾侧角指令,如图5和图6所示。飞行器在不机动情况下过载几乎为零,攻角稳定在6.4°附近;正弦机动时,攻角达到30°的最大值,倾侧角也被限定在60°以内。由于倾侧过程中攻角也进行了相应的调整,y向和z向过载存在相互耦合影响,因此得出的并不是完美正弦波形。在微分对策机动中,过载指令波动较小,两个过载通道也存在耦合。
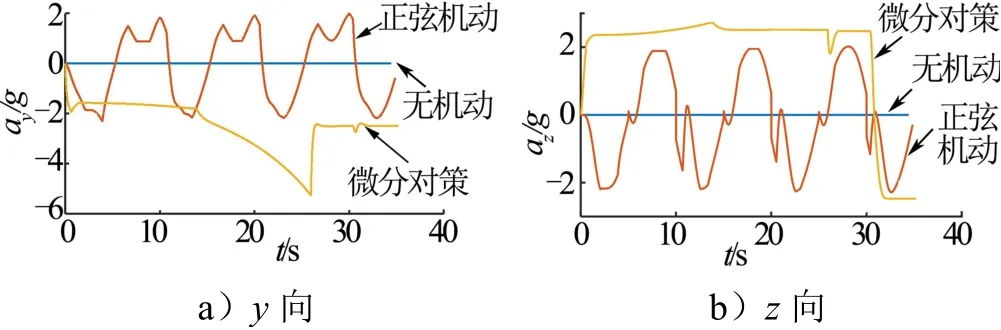
图5 飞行器y向和z向过载 Fig.5 Overload in y and z Directions
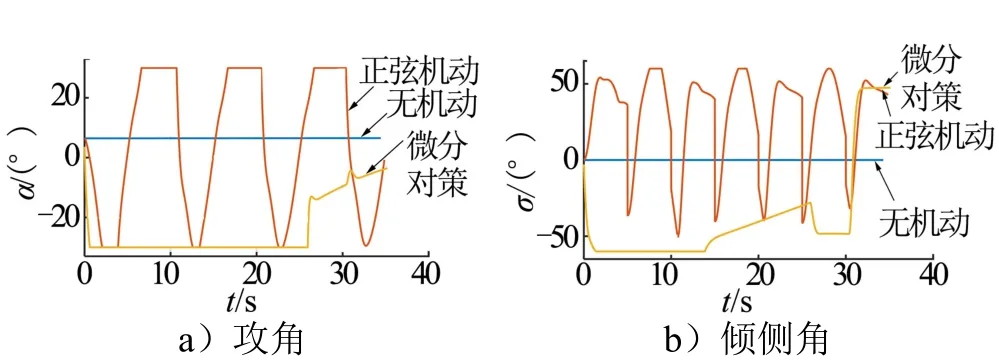
图6 飞行器攻角和倾侧角 Fig.6 Attack Angle and Bank Angle
拦截器过载如图7所示,在微分对策制导策略下,拦截器更早的达到了过载能力最大值,即为拦截微分对策式机动的飞行器,拦截器需要更强的机动能力。
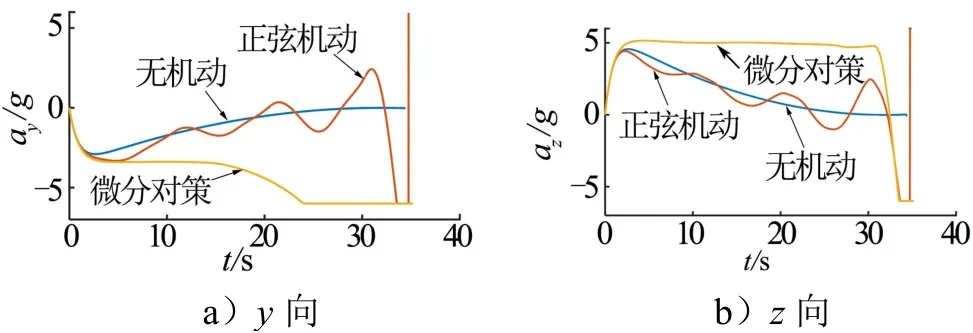
图7 拦截器y向与z向过载 Fig.7 y and z Overload of Interceptor
3.3 微分对策机动能力分析
该对抗场景下,微分对策制导律可以使飞行器实现有效机动,效果优于正弦机动,但是也存在高度波动大、末速低等不利于飞行的因素。为分析不同过载限制下飞行器的机动能力及高度、速度、过载等飞行参数的变化,在上述对抗场景不变的情况下,分别针对不同过载限制,对飞行状态进行仿真校验。表4为不同过载限制下飞行状态对比。随着过载限制的增加,飞行器的侧向机动距离增加,脱靶量也相应增大,如图8所示。
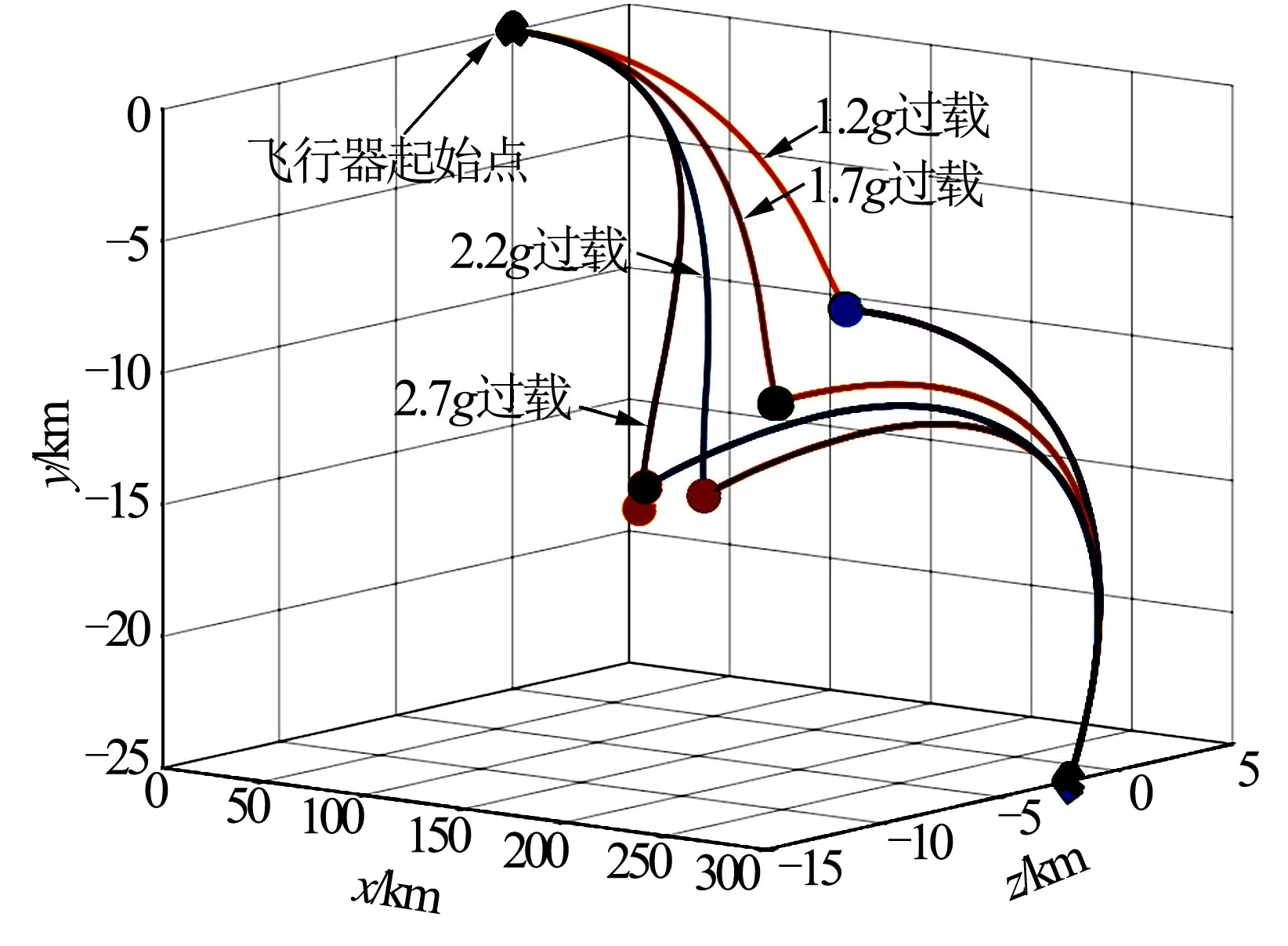
图8 不同过载限制下三维轨迹 Fig.8 3D Trajectory under Different Overload Limits
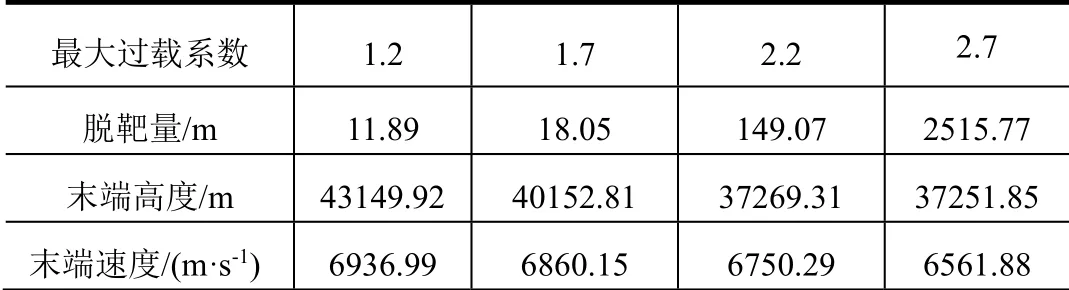
表4 不同过载限制下飞行状态对比 Tab.4 Flight State Comparison under Different Overload Limits
当过载系数超过2.2时,脱靶量达到149 m以上,此时飞行器的高度、过载波动大,而且末段高度和速度也随之降低(如图9~11所示)。
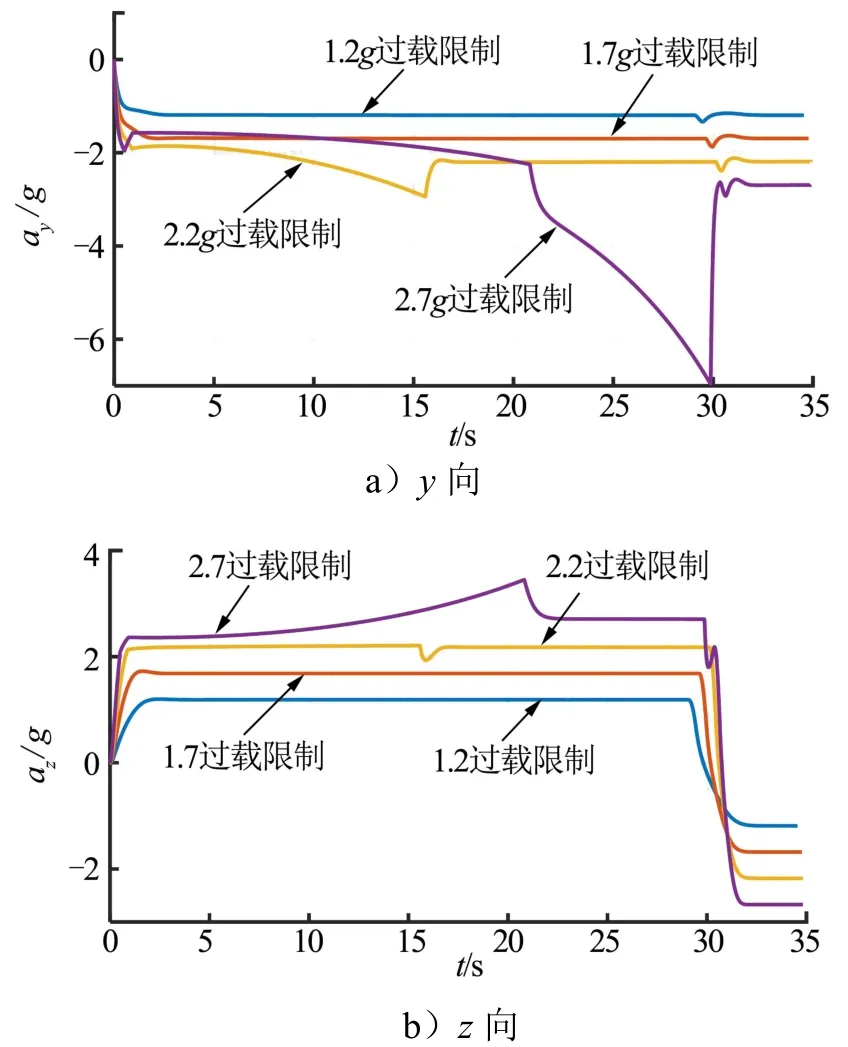
图9 不同过载限制下飞行器过载变化 Fig.9 Overload of Vehicle under Different Overload Limits

图10 不同过载限制下攻角和倾侧角变化 Fig.10 Attack and Bank Angle under Different Overload Limits
当最大过载限制较小时,整个飞行过程攻角和倾侧角都低于最大限制值,且变化平缓。当过载限制达到2.2g以上时,由于高度的降低以及攻角和倾侧角的耦合,在一定时间内实际过载值超过了规定值。例如:当过载限制为2.7g时,在21~31 s期间z向过载一直在限幅内,但是y向过载却超过了最大限幅,而且飞行器在从右倾变左倾的过程中过载也出现了较大幅度的波动。
图11中,在当前的对抗场景下,随着过载限制的增加,飞行器末段的高度和速度逐渐降低,在主动机动过程中消耗的能量相应增加。能量的消耗直接决定了飞行器能否完成既定任务,当过载限制较小时能耗虽然较低,但脱靶量也小,机动效果不佳。因此在实际工程应用中,飞行器的最大过载限制应综合考虑飞行器承受能力、能量消耗及机动效果。
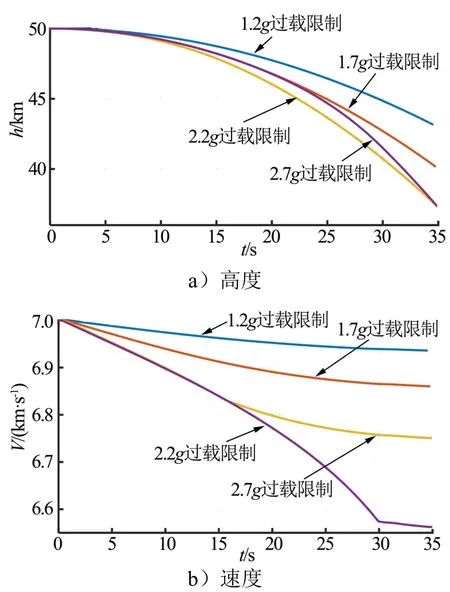
图11 不同过载限制下高度和速度变化 Fig.11 Height and Velocity under Different Overload Limits
4 结 论
针对再入飞行器滑翔中制导段的主动机动反拦截问题,设计了一种基于微分对策解析解的主动机动制导方法,建立了攻防博弈双方相对运动的数学模型,构建了脱靶量和能量消耗相关的对策性能指标,并基于合理假设推导出了微分对策理论的解析解。以比例导引拦截器为博弈对象设计双方博弈场景,将无机动、正弦机动、微分对策机动方法进行对比仿真分析,得出了基于微分对策的制导算法具有更强的机动性能,而且造成的最终脱靶量大、反拦截一方制导指令波动小,算法结构简单,易于工程实现。同时,针对微分对策制导律在不同过载限制下的飞行状态进行了仿真分析,在实际工程应用中应综合考虑飞行器最大过载承受能力、能量消耗以及机动反拦截效果,限定需用过载幅值,实现有效机动反拦截的同时最大限度保留射程能力。
