基于交叉熵优化的多飞行器在线协同目标分配方法

高 磊，刘也墨，尚 腾，何靓文

（北京航天自动控制研究所，北京，100854）

0 引 言

随着集群智能的快速发展，多飞行器自主协同作战受到各军事强国的高度重视，目前已成为研究的热点。飞行器自主协同作战技术涉及感知、规划、控制等多个领域，主要通过精准高效协同消解空间、时间、频率、任务、效果等多维度矛盾和冲突，最大限度发挥多飞行器的整体作战效能。在线协同目标分配技术是支撑多飞行器自主协同作战的关键，是综合考虑飞行器性能、战场环境和任务要求等多种约束条件，按照某种特定的优化准则，在飞行中实时计算求解各飞行器最优打击目标分配策略的一类共性技术，被规约为具有强实时、多约束、多目标、非线性特点的武器-目标分配（Weapon-target Assignment，WTA）问题[1]，其算法设计的实时性、最优性、有效性将直接对未来飞行器的协同作战能力产生决定性影响。

在线协同目标分配是一类NP-hard问题[1]，其特点是随着问题计算规模的扩大，解空间将出现“组合爆炸”情况，同时其最优解计算的时间代价也将呈指数级增加。目前学者大多采用匈牙利算法、蒙特卡洛树搜索（Monte Carlo Tree Search，MCST）、改进穷举法以及遗传算法（Genetic Algorithm，GA）、粒子群优化（Particle Swarm Optimization，PSO）等现代优化算法或其改进算法解决[2～6]。但由于飞行控制对待打击目标参数的在线计算速度要求较高，特别是飞行器和目标组合规模较大时，目前算法的计算实时性将很难满足实际工程应用需要，亟需对此进一步开展研究。近年来，有学者对交叉熵（Cross-entropy，CE）算法的优化效率进行了对比研究，证明了CE算法相较于MCST、GA、PSO等传统算法，在计算性能和解的全局最优性上有显著优势，或将成为未来的一个研究趋势[7,8]。因此，本文提出了一种基于交叉熵优化的多飞行器在线协同目标分配模型，首先结合飞行控制特点对多飞行器在线协同目标分配问题进行了数学建模，随后基于交叉熵理论设计了在线优化求解算法，并针对不同计算规模的问题开展了数学仿真分析和验证。

1 问题建模

多飞行器在线协同目标分配问题模型主要由飞行器和目标的先验条件、约束模型、指标评估函数3个部分组成。该问题相关要素可以抽象为一个三元组{ P ,C ,G}，其中，P表示飞行器和目标的先验条件集合，C表示目标分配的约束集合，G表示指标评估函数。

1.1 飞行器和目标的先验条件P

设定M架飞行器打击N个目标。已知飞行器i的位置 li= [ lxi,lyi,lzi]T，以及对目标j的打靶命中概率pij∈[ 0,1]、飞行器的剩余最大航程 Di；已知目标j的位置 qj=[ qxj,qyj,qzj]T，以及给定了目标价值 Vj∈ [ 0,1]。

1.2 目标分配的约束条件C

目标分配约束规定了解的形式和解的可行域 X*。本文采用分配策略矩阵描述问题的可行解，设在线协同目标分配的决策变量为X，记为：

式中 xij={0,1}。当将第i架飞行器分配第j个目标时，xij=1；当不将第i架飞行器分配第j个目标时，xij=0。同时，还需满足以下约束条件：

a）目标的分配数量约束：同一时刻，一个飞行器选择瞄准的目标数量不超过1个。

b）飞行器完全分配约束：在满足分配约束的前提下，所有飞行器均选择了瞄准目标。

c）剩余飞行能力约束：各飞行器距离所选瞄准目标的剩余航程估计值，需要满足在其最大可达航程的覆盖范围内。

1.3 指标评估函数G

为了对多飞行器在线协同目标分配策略的整体效能进行量化评估，从任务成本和任务收益两个方面构建指标评估函数。任务成本主要考虑多飞行器综合航程代价最小，以避免目标分配后可能面临的多飞行器航迹交叉问题；任务收益主要从最大综合命中概率和最大价值收益角度考虑，实现多飞行器协同作战整体效能的最优化。

a）任务成本cf。对于整个多飞行器而言，所分配的飞行总体航程越小，各飞行器越倾向于就近选择瞄准目标，可在一定程度上防止分配后航迹交叉现象的出现[9]。同时，执行任务所需的飞行航程总距离越小，其任务执行时间越短，途中面临战损的可能性越小。航程代价成本cf可按如下公式计算：

b）任务收益rf。认为各飞行器命中目标概率之间相互独立，那么对于目标j，其综合命中概率 jp为

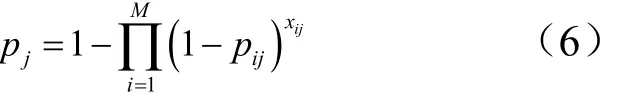
瞄准该目标的任务收益rjf可以记为

那么该分配策略的综合收益rf为

综上，指标评估函数的设计实质上是一个多目标优化过程，是为了使任务成本最低的同时，保证任务的收益最大。多目标优化整体收益f可以记为

对于上述指标的求解等价于求解多目标优化问题的Pareto最优解。由于上述评价指标间存在潜在冲突，难以同时达到最优值，采用加权方式对目标分配策略进行综合评价，计算公式如下：

式中 权重w1+w2=1， w1, w2∈ [ 0,1]。

综合考虑约束条件和指标评估，构建如下在线协同目标分配WTA模型：

2 在线优化算法设计

交叉熵算法解决组合优化问题最早由Rubinstein提出，在解决许多典型的NP-hard问题方面，被证实了具有很好的时效性。近年来年有学者以WTA问题为背景，对CE算法的性能进行了系统对比分析，证明了CE相比GE和MCST等算法在计算时间和解的最优性上具有更优的性能，特别是在收敛速度上优势明显[9]。为此，针对本文提出的在线协同目标分配模型，考虑到在线决策算法需要在有限时间内快速生成决策结果，基于CE设计优化求解算法。

针对上述非线性0-1整数规划问题，可以将其目标函数可等效建模为如下形式：假定S为定义在χ上的实值函数，χ为可行策略集，也称为决策空间。对规划模型的求解实质上是在满足约束条件的所有可行解中，找到目标函数S （X）的全局最小值γ*，此时对应的最优目标分配策略记为 X*。优化模型为[10]

上述问题的一组可行解X可视为一组由0、1构成的离散随机变量概率分布。基于上述思想，CE算法的思路是将该规划问题的最优解视为一个关于原始参数β的最优概率分布f （·,β），f （·,β）随着原始参数β的变化而改变。此时，优化过程的目标就是不断估计这个最优概率分布的过程，以使得当前的目标分配估计策略与理论最优策略的差异最小。选取交叉熵作为两个概率分布之间差异的测度。对于任意概率分布p，其相对概率分布q的交叉熵D （ p ||q）的计算公式为

那么对于上文中提到的S （X）最小值问题，求解过程是不断求解更优的估计γ来逼近*γ，这样就将优化问题转化为一个估计问题ℓ（γ） 。ℓ（γ） 可以表示如下[10]：

根据上式可以得到[8]：

综上，可以设计如下在线协同目标分配的CE优化算法：

a）初始化原始估计参数ˆβ为均匀概率分布种子：

b）设置采样门限阈值θ∈[ 0,1]；

c）根据ˆβ随机生成满足分配约束的K组目标分配策略样本 X1,X2,… ,XK，并根据指标函数f计算（Xi）,i =1,2,…,K；

e）根据筛选出的样本，按照下式更新原始估计参数ˆβ：

重复步骤c～e直至ˆβ收敛至最优参数β，判定依据为指标函数值连续5次不变。

3 仿真分析

为验证交叉熵优化算法解决在线协同目标分配问题的有效性，采用C++作为算法开发语言，分别实现了6架飞行器打击3个目标、12架飞行器打击3个目标、12架飞行器打击6个目标、24架飞行器打击6个目标、24架飞行器打击12个目标、48架飞行器打击12个目标6种场景的仿真，在不同的计算规模下对算法性能进行系统分析和验证。仿真初始参数的设置如下：目标价值 jV= 1，命中概率 ijp= 0.8，剩余航程能力 Di= 250 km，指标分配权重w1=w2= 0.5，样本容量N=200，采样门限阈值θ=0.1，最大迭代次数nItermax=50，算法终止的判定次数 Ncheckmax=5，收敛精度peps=0.0001。仿真结果见图1。

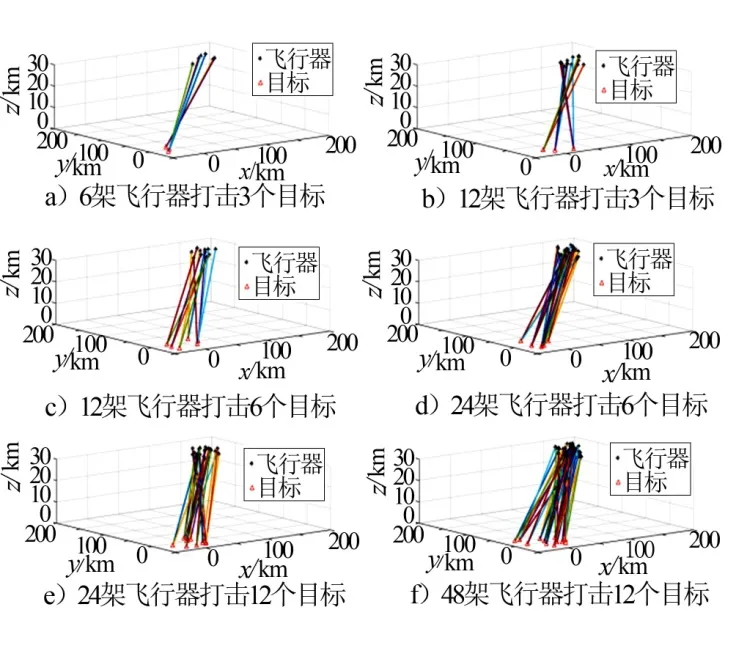
图1 在线协同目标分配策略仿真结果 Fig.1 Simulation Results of Real-time Cooperative Target Allocation Strategy

图2为在线协同目标分配优化过程。

图2 在线协同目标分配优化过程 Fig.2 Optimization Process of Real-time Cooperative Target Allocation

由图1、图2可以看出，在不同计算规模下，对于本文提出的多约束、非线性0-1整数规划模型，基于CE的在线协同目标分配优化算法能够在接近20次左右的迭代中快速收敛，并且从综合航程代价、协同突防命中等角度给出合理的目标分配结果。从表1可以看出，CE算法在各种计算规模下的平均求解时间在毫秒级，典型6架飞行器打3个目标情况下一次在线决策时间仅需8.7 ms，在最大计算规模场景下的在线优化时间仅需140.9 ms，能够很好地满足工程应用需求。

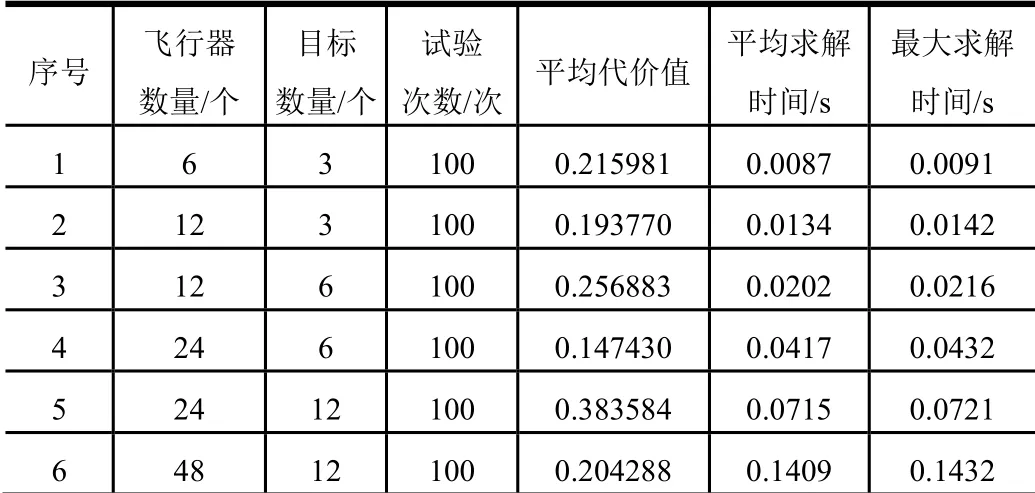
表1 在线协同目标分配性能分析 Tab.1 Performance Analysis of Real-time Cooperative Target Assignment

4 结束语

多飞行器在线协同目标分配问题是一个具有多约束、强实时限制条件的复杂0-1整数规划问题，除了考虑分配策略求解的全局最优性，还需要兼顾其在线计算的实时性要求，以便为飞行控制提供实时的目标指引信息，提升飞行控制效率。本文基于交叉熵优化提出了一种多飞行在线协同目标分配的建模及优化方法，经设计并通过数学仿真验证了本文算法的有效性，可为未来多飞行器自主协同作战的实现提供技术支撑。