miniSAR 卫星精密参考轨道设计
2023-01-12廖祥郑靖许永生谢成清丁强强
廖祥, 郑靖, 许永生, 谢成清, 丁强强
(1. 深圳市魔方卫星科技有限公司, 深圳 518129; 2. 深圳航天东方红卫星有限公司, 深圳 518057)
2015 年以来,多个国外商业航天初创公司相继提出并部署各自的轻小型合成孔径雷达(mini synthetic aperture radar,miniSAR)卫 星[1]。 在 此背景下,深圳航天东方红卫星有限公司瞄准市场前景广阔的高分辨率微波成像和形变测量应用领域的miniSAR 卫星项目,并立项研发,计划2021年底具备发射条件。 为实现高精度长时间序列的形变监测,miniSAR 卫星的重轨干涉基线设计优于500 m,要求卫星在轨任务期间的三维空间回归轨迹被控制在直径为500 m 的管道内。
管道指以卫星运行轨道的参考轨迹为中心、干涉基线极大值为直径的三维空间[2]。 以国外早期干涉SAR 卫星项目为例,ERS-1/ERS-2 管道设计直径为600 m[3],TerraSAR-X 为500 m[4],ALOS/ALOS-2 为1000 m[5],Sentinel-1 则 达 到 了150 m[6-7]。 由于SAR 卫星一般运行在500 ~800 km高度范围内的低地球轨道空间,大气阻力与太阳光压等非保守摄动力会对卫星轨道根数造成长期影响,如此高精度的管道控制要求,需设计高精度参考轨迹为基准,进一步实施精密轨道控制[8]。而参考轨迹由参考轨道预报一个回归周期生成,因此,干涉SAR 卫星高精度轨道控制中一个十分重要的术语“参考轨道”被提出。
参考轨道指在仅考虑中心天体保守力情况下,满足预报一个回归周期后卫星地固系下的三维空间位置完成重合的一类轨道。 参考轨道仅为一组包含历元的轨道根数,其最终类型为瞬时轨道根数(又称密切轨道根数),坐标系通常为惯性系瞬时真赤道地心坐标系(true of date,TOD)[9]。对于需要生成长期一致的时间序列干涉数据的SAR 卫星,参考轨道一旦完成设计,在整个任务周期内就不能更改,这同时对重轨单星和双星近距编队干涉SAR 系统构成约束。
由于干涉SAR 卫星技术起步较晚,且工程任务较少,国内外关于参考轨道设计的文献较欠缺。推导严密、可复现性好的精密参考轨道设计文献更是稀缺。 文献[10]针对TerraSAR-X 任务,实现了一种基于虚拟速度增量与序列二次规划的参考轨道优化设计方法,但由于引入了2 次虚拟轨控,生成的参考轨迹不连续;文献[11]提出基于迭代修正方法的严格回归轨道设计,但文中的推导存在部分错误,实现算法存在缺陷,且回归精度较差;文献[12]提出一种基于高阶地球重力场模型的严格回归轨道单目标优化设计方法,但回归精度较差,仍在米级;文献[13]在修正文献[10]方法的同时,解决了利用倾角偏置修正沿迹向长期漂移的问题,但文中采用专有工具优化设计参考轨道,无法获取具体实现算法。
本文基于嵌套式迭代修正思想,通过合理选择参考系、初始预估参数、平根与轨道外推模型,并合理设置迭代修正反馈值及迭代收敛判据,建立了一套推导严密、可复现性好的miniSAR 卫星精密参考轨道设计算法,由其设计的参考轨道生成的参考轨迹在地固系下的闭环精度达毫米级。
1 参考轨道特性分析
miniSAR 卫星的参考轨道必须同时具备2 个基本特性:①轨道必须是回归轨道,即运行在该轨道上的卫星对星下点具有高精度重访特性;②轨道必须是冻结轨道,即卫星星下点重访时轨道高度的一致性。 根据轨道动力学原理,回归轨道特性与轨道半长轴a和倾角i相对应,冻结轨道特性与偏心率e和近地点幅角ω相对应[10]。
此外,考虑到卫星能源的稳定性及升交点赤经的进动速率,miniSAR 卫星的参考轨道还设计具备太阳同步轨道特性。 这一特性进一步约束了参考轨道半长轴a和倾角i之间的关系[14]。
1.1 太阳同步特性
太阳同步轨道平面法线与太阳矢量在赤道平面上的投影保持着固定的夹角关系,这使得运行其上的卫星可获得稳定的光照条件,且在卫星飞越相同地理纬度的目标区域处于同一地方时。 太阳同步轨道的设计主要考虑降交点平地方时(mean local time, MLT)与平均轨道高度(mean orbit altitude, MOA)2 个参数。
文献[15]指出,太阳同步轨道倾角平根受太阳引力影响的长期摄动年变化率di/dt(°/年)与降交点MLT 成正弦关系,降交点MLT 为3:00、9:00、15:00、21:00 时di/dt最 大,降 交 点MLT 为0:00、6:00、12:00、18:00 时di/dt最小并接近于0,如图1 所示。 因此,在设计太阳同步轨道参数时,干涉SAR 卫星适合选择0:00、6:00、12:00、18:00 附近的降交点MLT,以减小倾角平根的长期漂移,进而避免不必要的倾角调整。

图1 受太阳引力影响的倾角长期项摄动[15]Fig.1 Secular perturbation of inclination due to gravity of the Sun[15]
MOA 的设计则需考虑SAR 卫星载荷在一个回归周期T内可实现对全球的无缝覆盖。 这里的覆盖能力并非实际可照射区域,而是卫星在姿态最大侧摆角下载荷所能覆盖的区域来计算。 由于SAR 载荷一般具有照射盲区,因而MOA 的设计需要对此因素加以建模分析。
确定好降交点MLT 与MOA 后,可根据基于J2低阶引力摄动下的太阳同步轨道设计方程进一步确定轨道倾角:
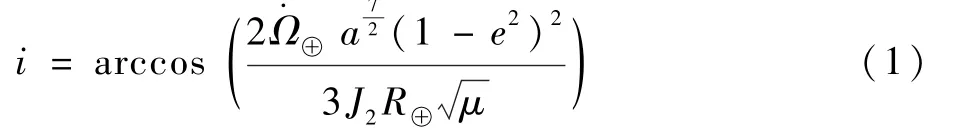
式中:μ为地球引力常数;R⊕为地球平均半径;为地球公转升交点赤经进动速率;J2为地球非球形引力模型二阶带谐项系数。
1.2 回归特性
理想的参考轨迹在地固系三维空间下为首尾完全闭合的曲线,因而参考轨道必须具有回归特性。 给定回归周期T与对应的回归圈数N,则回归轨道约束方程为
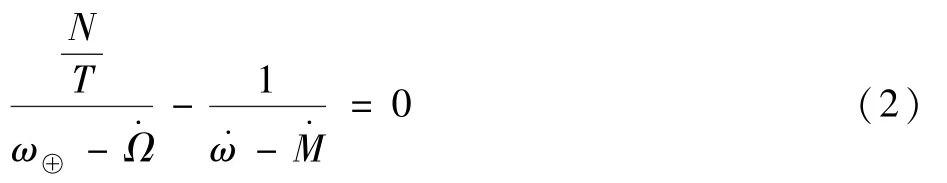
式中:ω⊕为地球自转速率;分别为升交点赤经、近地点幅角、平近点角的进动速率,三者在J2低阶引力摄动下的解析式[16]为
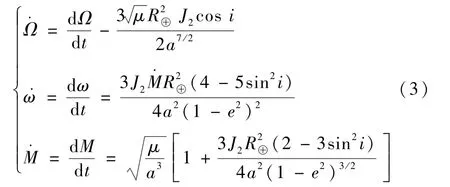
式中:倾角i以式(1)为约束参与式(3)对半长轴a的求解;Ω为升交点赤经;ω为近地点幅角;M为平近点角。
1.3 冻结特性
理想参考轨迹的星下点重访时轨道高度保持不变,因而参考轨道必须具有冻结特性。 冻结轨道有2 种类型:①临界倾角的冻结轨道;②小偏心率近圆冻结轨道。 干涉SAR 卫星的参考轨道属于第2 种情况。 冻结轨道设计方程为

根据小偏心率近圆冻结轨道的要求,考虑J2及J3低阶引力摄动可解算得到
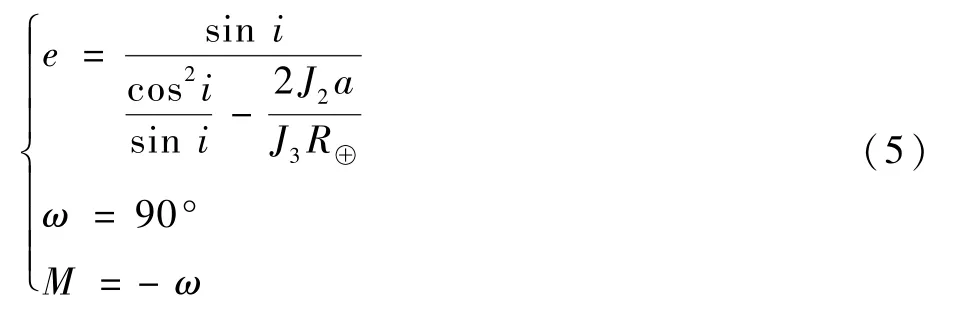
式中:J3为地球非球形引力模型三阶带谐项系数。
1.4 参考轨道预估值
综上对参考轨道特性的分析,可预估得到5 个基于低阶引力势场的参考轨道根数:

需要指明的是,此处获得的参考轨道初值为TOD 坐标系下的平根,在使用之前须将其转换为瞬根方可作为初始输入参与后续迭代修正过程:
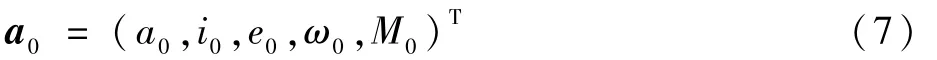
式中:a0、i0、e0、ω0、M0分别为半长轴、倾角、偏心率、近地点幅角、平近点角的瞬根。
2 参考轨道设计算法
参考轨道的设计包含两部分工作:①针对(a,i)组合的太阳同步回归轨道的优化设计;②针对(e,ω)组合的冻结轨道的优化设计。 但由于(a,i)迭代修正的输入为预估的参考轨道根数,2种组合优化设计方法需嵌套使用。 当(e,ω)迭代收敛之后,只需再重复一轮(a,i)迭代修正即可实现高精度回归。 具体算法流程如图2 所示。
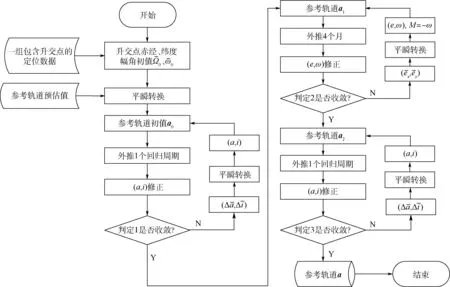
图2 精密参考轨道设计算法流程Fig.2 Algorithm flow chart of precise reference orbit design
2.1 迭代修正具体实现
从算法流程可见,参考轨道设计过程主要分为3 个步骤:①(a,i)组合迭代粗修正;②(e,ω)组合迭代修正;③(a,i)组合迭代精修正。
2.1.1 (a,i)组合迭代粗修正
(a,i)组合迭代粗修正以参考轨道初值a0为输入,外推1 个回归周期T,利用首尾轨道数据生成平根修正量(Δ¯a,Δ¯i),并进一步通过平瞬转换获得新的(a,i)值,其余轨道根数保持不变。 其中,(¯)为实际获得的平根修正量,(a,i)则为最终修正得到的瞬根值。 ()根据梯度矩阵获得
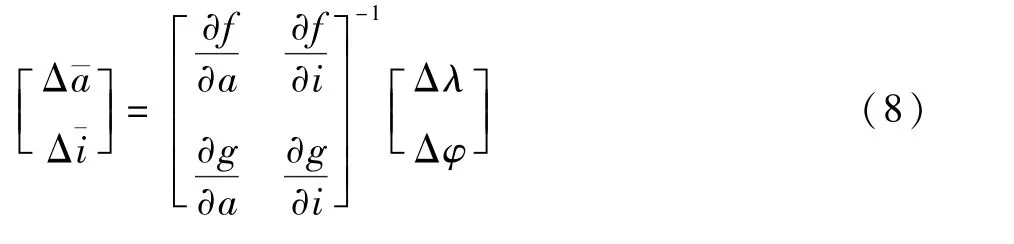
式中:Δλ和Δφ分别为首尾轨道数据星下点经纬度之差;4 个偏导数求解式为
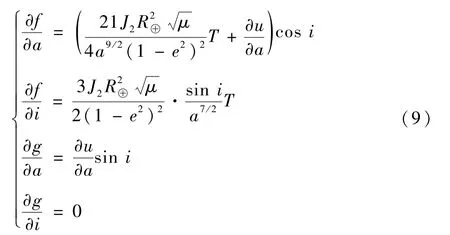
其中:中间量∂u/∂a计算如下:
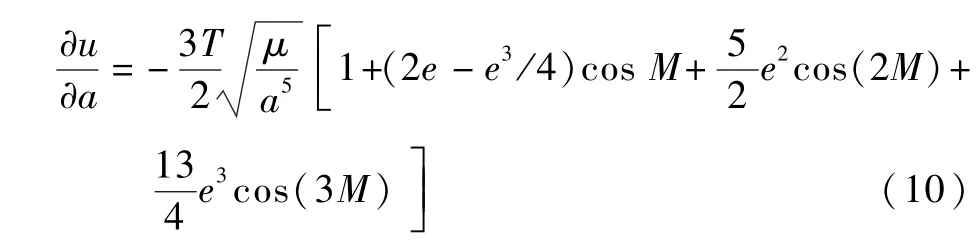
式(8) ~式(10)为最终算法,其详细推导过程可参考文献[10-12],但注意式(9)对文献[11]中错误部分的更正。
2.1.2 (e,ω)组合迭代修正

图3 偏心率平根矢量修正示意图Fig.3 Diagram of mean eccentricity vector correction

2.1.3 (a,i)组合迭代精修正
(a,i)组合迭代精修正的实施方法与2.2 节
步骤1相同,但本节迭代修正的收敛判据与2.2 节步骤1 不同。
2.2 收敛判据
(a,i)与(e,ω)组合每轮修正需要多次迭代实现收敛,参考轨道设计算法的3 轮组合修正都需要给定明确的收敛判据,用以判断每次迭代后的结果是否满足收敛条件,各轮修正的收敛判据如下。
步骤1判定3。 以前后2 次迭代修正后的参考轨道根数,预报1 个回归周期T之后的三维空间轨迹回归精度优于精密定轨精度为收敛准则。 参考GNSS 精密定轨精度为厘米级,故收敛准则设置为

式中:n为迭代次数,n≥1;为参考轨迹闭环回归精度,计算式为
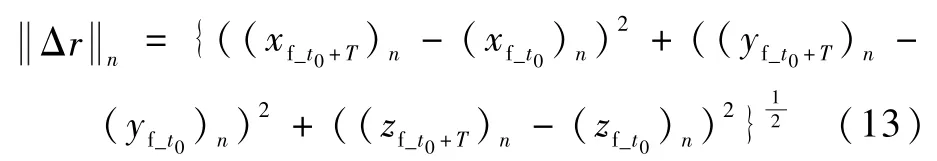
式中:xf、yf、zf分别为地固系三维坐标值,时间下标t0、t0+T表征预报1 个回归周期T所得轨道数据的首、尾坐标值。
步骤2判定2。 以前后2 次迭代修正后的偏心率平根矢量偏差引起的参考轨迹偏差¯aΔ¯e优于厘米级为收敛准则。 由于¯a为10-6m量级,故偏心率平根矢量前后差异需优于1.0 ×10-8,即
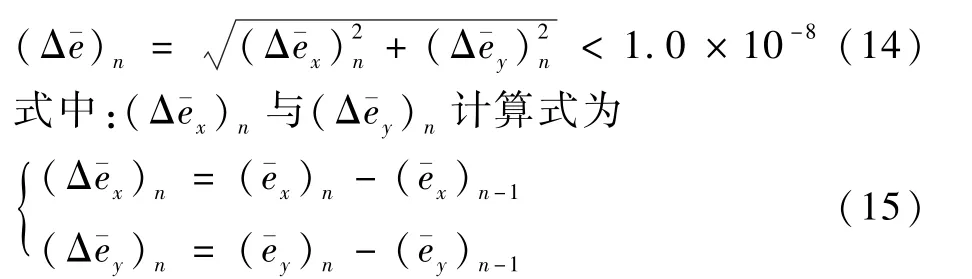
步骤3判定1。 以前后2 次迭代修正后的参考轨道根数预报1 个回归周期T之后的三维空间轨迹回归精度无明显提高为收敛准则。 考虑二阶展开,回归精度差异需优于o(),即
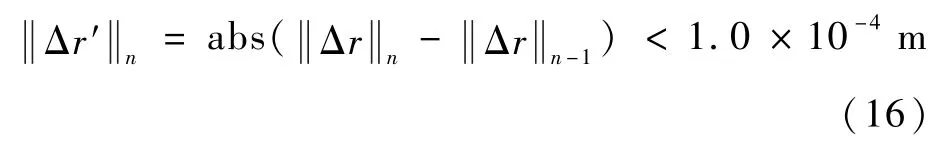
式中:abs()表示取绝对值;n为迭代次数,n≥2。
2.3 平瞬转换
参考轨道设计算法的迭代实际修正量为平根,但参考轨道的形式为瞬根,因此在修正平根后需执行平瞬转换获得瞬根修正值。
常用的平瞬转换模型有多种[16],本文选用考虑J2~J6及摄动的Eckstein-Hechler 模型[17],该模型专门针对小偏心率冻结轨道进行优化,尤其适合参考轨道设计过程。
Eckstein-Hechler 模型在基于SCILAB 科学计算语言的Celestlab[18]与基于Java 语言的Orekit[19]这2 套成熟开源航天动力学库中皆有实现,可作为实现参考。
2.4 外推模型
(a,i)与(e,ω)组合迭代修正的过程皆需要进行轨道外推,以获得向后一段时间的轨道数据。由于参考轨道只考虑中心天体保守力,因而外推模型的动力学只考虑高阶地球非球形引力,本文为100 ×100 阶的EGM2008 引力模型[20]。
动力学模型的单一决定了外推模型的精度取决于积分器的选择及对积分步长的控制。 考虑到积分效率与精度,选择9 阶误差控制的8 阶Runge-Kutta-Verner 积分器RKV8(9)[21]。 修正过程中,误差容限设为优于1.0 ×10-13,(a,i)、(e,ω)组合迭代修正最大步长分别控制在10 s、5 s 以内。
3 数值实验
3.1 输入数据与实验条件
3.1.1 轨道特性输入
miniSAR 卫星轨道设计为具有10 天/151 轨(回归周期为10 天,10 天内卫星运行151 轨)回归、冻结特性的太阳同步轨道,标称降交点MLT为6:00(晨昏轨道),卫星质量为180 kg。
3.1.2 定位数据输入
卫星成功入轨后经运控系统提供一组包含升交点的定位数据,如表1 所示(表中为仿真的地固系三维位置与速度值)。 对其插值得到升交点处地固系状态矢量,对应历元t0为2021-01-01,00:26:13.511 668 UTCG。 再利用升交点处的地固状态矢量计算得到升交点赤经平根初值为=10.881 803 934°。
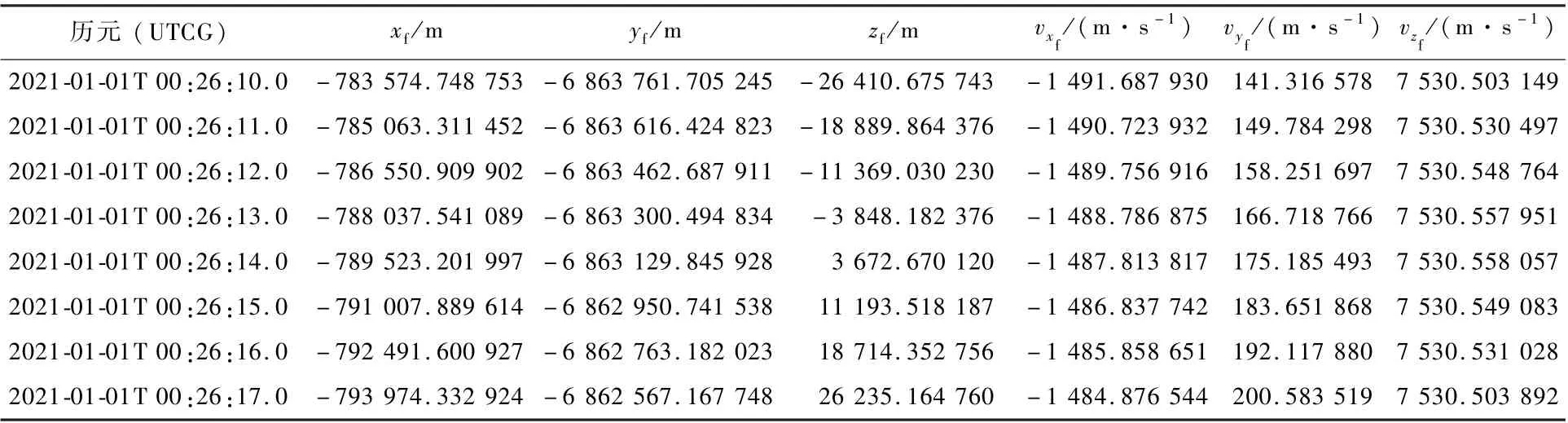
表1 定位数据Table 1 Precision positioning data
3.1.3 参考轨道初值
根据轨道特性预估值与定位数据,计算得到的参考轨道在t0时刻的初值为

平瞬转换后参与迭代修正的参考轨道初值为

3.1.4 实验条件
数值实验基于MATLAB 语言环境,轨道外推与数据报表使用STK Engine 的MATLAB 编程接口实现,平瞬转换算法移植自Celestlab。 仿真程序运行于搭载Windows 10 专业版操作系统的联想P52 移动工作站,机带内存32 GB,处理器型号为Intel Xeon E-2176M。
3.2 实验结果
表2 给出了参考轨道初值及数值实验过程中3 轮迭代修正所得参考轨道根数,其中a为最终获得的参考轨道根数。 从表2 中数据可见,由a0到a1及a2到a的过程中,只有半长轴与倾角是变化量;由a1到a2的过程中,只有偏心率、近地点幅角与平近点角是变化量。
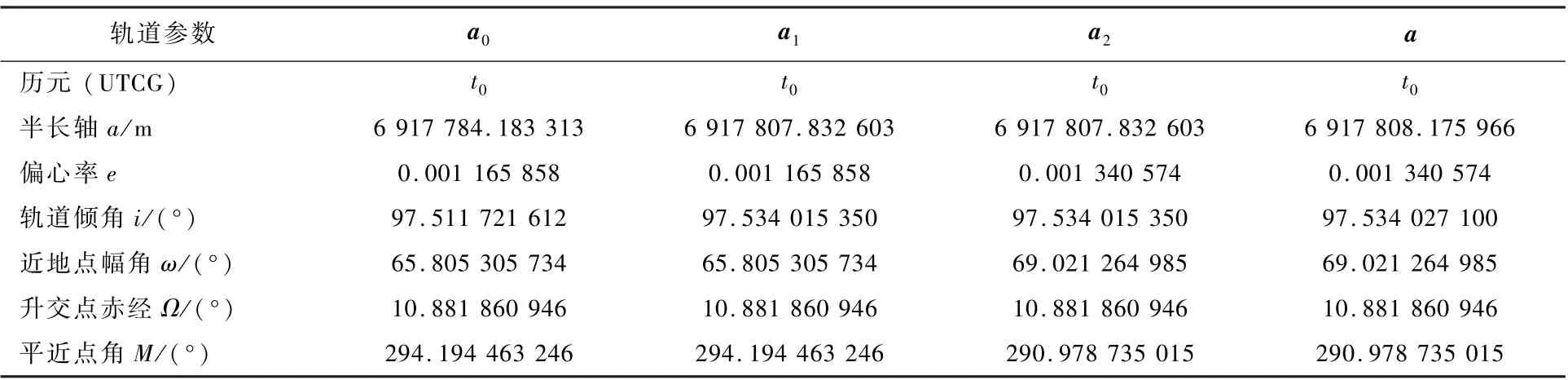
表2 迭代修正过程中所得参考轨道根数(TOD 瞬根)Table 2 Reference orbit elements obtained during process of iterative correction (TOD osculating elements)
表3 给出了3 轮修正迭代过程中收敛判据的统计数据,图4 ~图7 则对统计数据进行了可视化。 其中,图4 与图5 对应第1、2 轮(a,i)组合迭代修正过程中的收敛情况,横坐标n为迭代次数,图6 与图7 则对应(e,ω)组合迭代修正过程中偏心率平根矢量收敛情况。 统计数据表明:
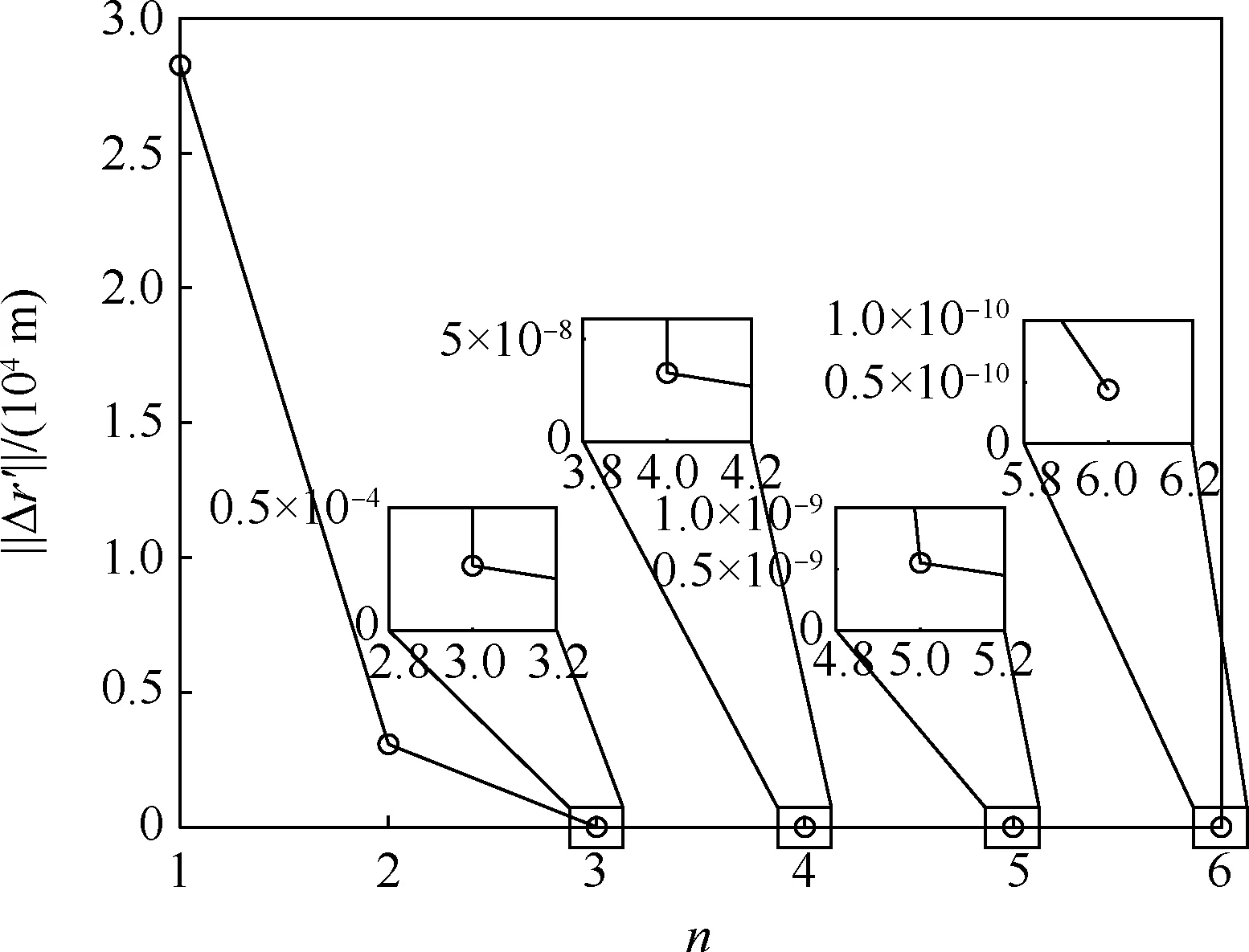
图4 第1 轮(a,i) 迭代修正收敛情况Fig.4 Convergence of first (a,i) iterative correction
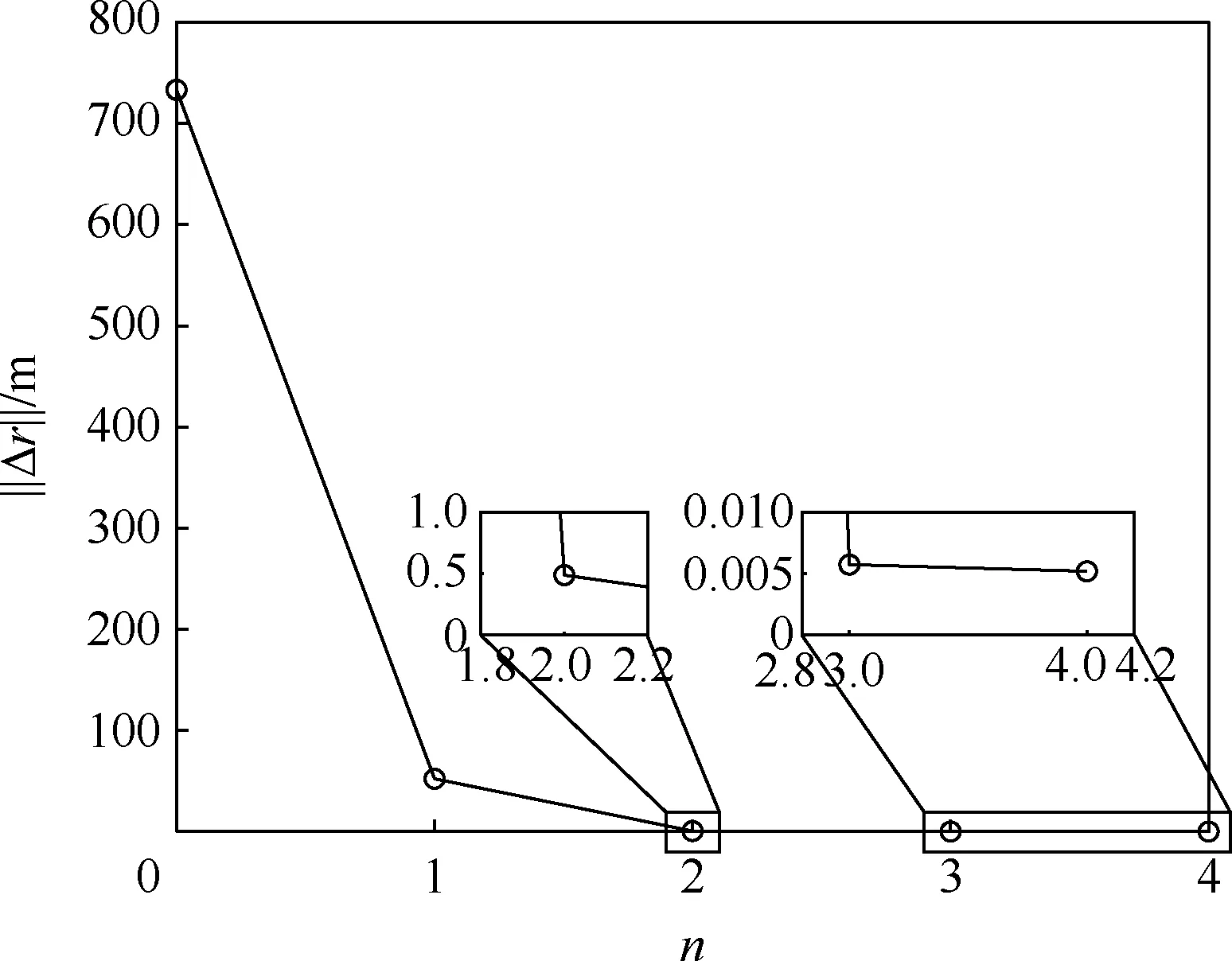
图5 第2 轮(a,i) 迭代修正收敛情况Fig.5 Convergence of second (a,i) iterative correction

图6 偏心率平根矢量收敛情况Fig.6 Convergence of mean eccentricity vector
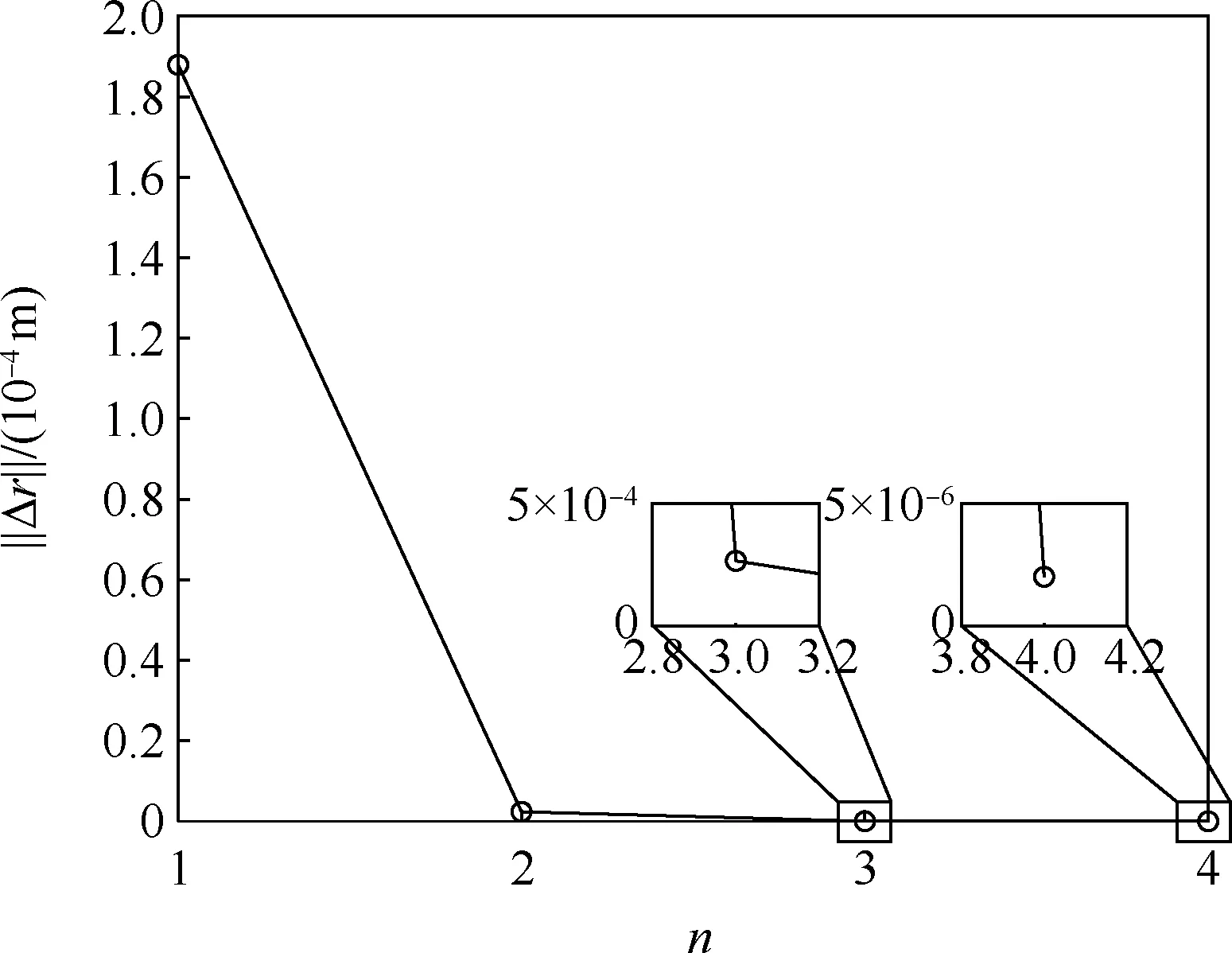
图7 (e,ω)迭代修正收敛情况Fig.7 Convergence of (e,ω) iterative correction

表3 迭代修正收敛数据Table 3 Convergence data of iterative correction
1) 第1 轮(a,i)组合迭代修正过程中,仅6 次迭代即实现收敛,收敛精度达4.38 ×10-7m。
2) (e,ω)组合迭代修正过程中,120 天内以1 个回归周期为步长的偏心率平根矢量在迭代修正过程中逐步收缩半径,仅4 次迭代偏心率平根变化率Δ¯e即收敛至2 ×10-10。
3) 第2 轮(a,i)组合迭代修正过程中,仅4 次迭代即实现收敛,收敛精度优于0.006 m。
综合本节所述,实验结果的收敛精度满足收敛判据指标,验证了所提miniSAR 卫星参考轨道迭代修正设计算法的有效性和精密性。
实验中,单次(a,i)修正平均耗时56.64 s,单次(e,ω)修正平均耗时624.45 s,合计耗时47.29 min。卫星轨控任务周期一般大于轨道周期,合计耗时小于miniSAR 卫星约95.36 min 的轨道周期,不影响轨控任务正常开展。 此外,考虑到软硬件条件,参考轨道设计工作不适合在内存低于GB 级的嵌入式星载计算机上进行。
4 结 论
本文建立了一套完整的miniSAR 卫星精密参考轨道设计算法,经过嵌套式(a,i)、(e,ω)组合的3 轮迭代修正获得了毫米级三维空间轨迹回归精度。
1) 引入了参考轨道的具体定义,提出的参考轨道设计算法流程清晰、推导严密、收敛判据明确、可复现性好。
2) 提升了参考轨道设计速度与精度,数值实验在48 min 内获得了地固系三维空间闭环回归精度约为0.005 m 优于0.01 m 的精密参考轨道,满足实际工程应用需求。
