基于PCC-LSTM 模型的短期负荷预测方法
2023-01-12刘倩倩刘钰山温烨婷何杰李晓毕大强
刘倩倩, 刘钰山,*, 温烨婷, 何杰, 李晓, 毕大强
(1. 北京航空航天大学 自动化科学与电气工程学院, 北京 100191;2. 清华大学 电机系, 北京 100084)
由于电能难以大量存储及负荷需求时变等特点,要求发电、输电、用电要时刻保持动态平衡。电力负荷预测准确率的提高有助于保证电力系统安全可靠运行和提高发电机组的利用率[1],根据预测时间长度分为超短期负荷预测、短期负荷预测、中期负荷预测和长期负荷预测[2]。 超短期负荷预测是对当前时刻后的有限时刻进行预测,主要用于实时调度;短期负荷预测是对一天中的每个时刻进行预测,主要用于制定发电日计划;中期负荷预测是对月度负荷进行预测,主要用于月度检修;长期负荷预测是对年度负荷进行预测,主要用于年度检修。
电力系统短期负荷预测是一种基于历史的负荷数据,充分考虑系统的运行特性、天气状况、经济发展情况、工作日和节假日等影响因素,来预测未来一天内的电力负荷用电情况[3]。 负荷数据的精准预测有利于改善电力系统的运行规划和实时调度,对电力系统的稳定性大有裨益[4]。
目前,对电力负荷的短期预测方法主要分2 类:传统预测方法和机器学习方法[5]。 传统预测方法有回归分析法[6-8]、灰色模型法[9-10]、模糊预测法[11]、自回归积分滑动平均模型[12-13]等。 这些方法简单、速度快,但多是基于线性关系模型,反映非线性关系的能力有限。 机器学习方法有随机森林[14]、支持向量机[15]、专家系统[16]、人工神经网络预测法[17]、深度学习法[18]等。 人工神经网络预测法中的长短期记忆(long and short term memory, LSTM)神经网络擅于处理序列型数据,可以有效减小负荷预测模型需要的数据量维度,充分挖掘时序数据间的内在关系,相较于其他的机器学习算法有较高的准确性。
LSTM 神经网络基于循环神经网络(recurrent neural network, RNN),通过增加遗忘门、输入门和输出门,有效解决了梯度爆炸和梯度消失的问题。 在电力负荷预测中,LSTM 神经网络取得了一定的成果。 文献[19] 建立了基于Attention-LSTM 的短期负荷预测模型计算用电量预测值。文献[20]构建了3 层LSTM 深度学习负荷预测模型用于预测电力负荷。 文献[21]提出了一种深度双向长短期记忆(deep bidirectional long and short term memory, DBiLSTM) 和多元线性回归(multiple linear regression, MLR)组合预测模型。文献[22]提出了一种小波分解-最小二乘支持向量机长短期记忆( wavelet deromposition-least squares support vector machine-LSTM, WD-LSSVMLSTM)神经网络组合模型预测短期负荷。 文献[19-22]研究均采用LSTM 神经网络训练数据,但在选择输入量时,不是未根据影响因素和电力负荷数据的相关关系选择更合适的影响因素作为输入量,就是对输入量的处理过于繁琐。
为提高负荷预测的准确率,本文提出了一种基于Pearson 相关系数-LSTM(Pearson correlation coefficient-LSTM, PCC-LSTM)模型的多因素短期负荷预测方法。 首先对各类影响因素做Pearson相关性分析,确定与电力负荷变化的相关程度,选出合适的负荷预测参数作为LSTM 神经网络的输入量,然后将其输入到由LSTM 网络层和全连接层构成的模型中进行预测。 由于使用了Pearson相关性分析方法,PCC-LSTM 模型有效增强了输入数据与预测数据之间的相关性,可以显著降低负荷预测误差。
1 基本原理
1.1 Pearson 相关系数
PCC 是为了分析2 个变量间的相关程度。 2个任意变量X、Y间的PCC 可表示为
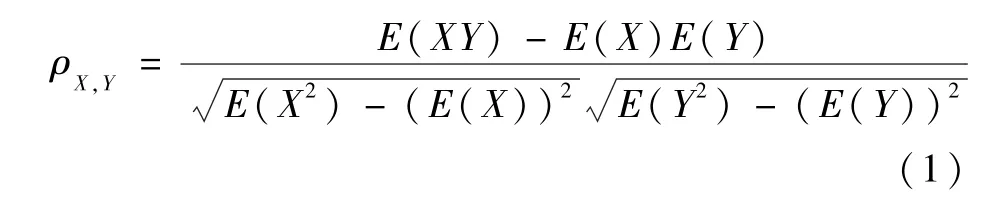
式中:ρX,Y为变量X、Y的相关性系数;E为样本的数学期望。
当X、Y两变量无关时,PCC 为0;当X、Y两变量负相关时,PCC 在-1 ~0 之间;当X、Y两变量正相关时,PCC 在0 ~1 之间。 变量的相关程度由相关系数的绝对值表征,绝对值越大相关性越强,具体的系数范围和相关程度如表1 所示。

表1 相关系数范围Table 1 Range of correlation coefficients
1.2 LSTM 神经网络模型
LSTM 神经网络是一种改进的RNN,通过精巧的网络结构设计,可以学习时间序列中的长短期依赖信息。 其网络结构如图1 所示。

图1 LSTM 神经网络结构Fig.1 Structure diagram of LSTM neural network
LSTM 神经网络结构包括遗忘门、输入门和输出门。 遗忘门决定当前细胞需要遗忘的部分,输入门决定当前细胞需要保留的向量,输出门决定当前细胞的输出内容,如式(2) ~式(7)所示[23]:
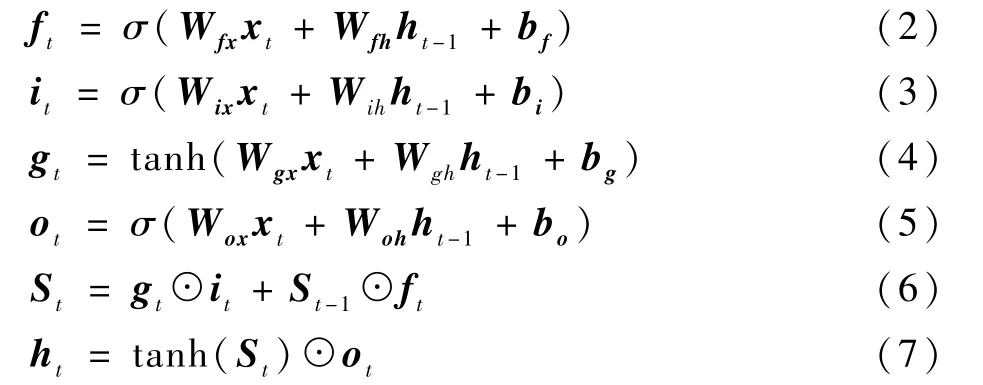
式中:ft、it和ot分别为遗忘门、输入门和输出门;xt、gt、ht和St分别为输入量、输入节点、中间输出和状态记忆单元;Wfx、Wfh、Wix、Wih、Wgx、Wgh、Wox和Woh分别为对应门的矩阵权重;bf、bi、bg、bo分别为对应门的偏置;⊙为矩阵的哈达玛积;σ为sigmoid 激活函数,可以表示为

2 PCC-LSTM 模型
2.1 PCC-LSTM 模型结构
图2 为PCC-LSTM 模型结构。 PCC-LSTM 模型主要包括2 部分:Pearson 相关性分析主要负责选取合适的影响因素作为输入量,LSTM 神经网络主要负责负荷预测。 采用给出的数据,对影响因素做Pearson 相关性分析,初步判断所选取的因素是否会真正对负荷用电量产生影响。
除此之外,休闲运动还需要学校予以一定的支持,为学生进行休闲运动提供良好的场地条件,教师也应该加强对于休闲运动方式、项目的研究,从而以更加专业化的形式给予学生正确的指导。学校也可以定期举办休闲运动项目的活动,如组织学生在节假日,一起走出校门和深入大自然之中,开展郊游、登山、骑山地自行车、徒步越野等一系列空域、陆域、水域休闲体育项目。这些休闲项目操作简单,对于学生的要求较低,而且这些休闲体育项目都是对于日常基本动作技能的练习,对于学生日常生活有着很好的帮助,能够使学生在日常生活当中也进行自身的锻炼,加强了学生的身体素质。
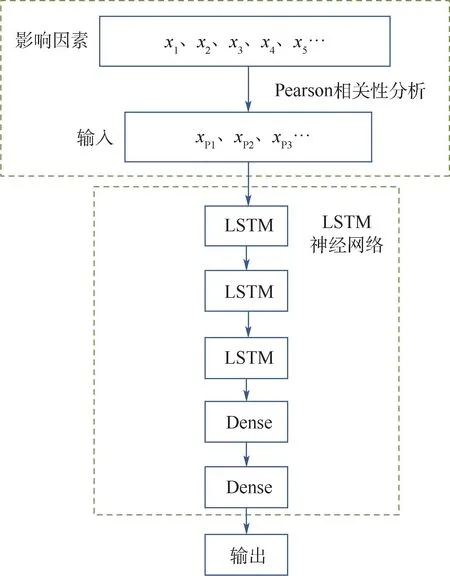
图2 PCC-LSTM 模型Fig.2 PCC-LSTM model
通过增加LSTM 的层数来增加预测模型的深度可以增强预测能力,故本文的预测模型包括3 个LSTM 网络层。 在每个LSTM 网络层后采用Dropout 方法防止模型过拟合。 在LSTM 后加一个全连接层(Dense),该全连接层可以汇集不同时间段的历史数据对预测点的影响,对影响进行综合后,最终再通过一个全连接层输出,得到预测日24 个时间点的电力负荷用电量。
2.2 损失函数
模型训练过程中,使用Adam 优化算法更新神经元的权重项矩阵和偏置项矩阵,寻找损失函数的最小值[24]。 采用均方误差函数为
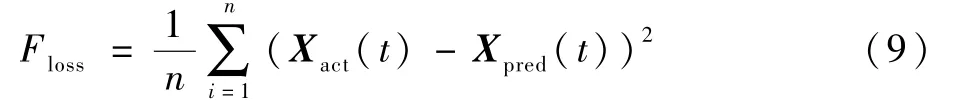
式中:n为样本个数;Xact(t)和Xpred(t)分别为样本数据的实际值和预测值。
2.3 实验评价指标
使用平均绝对百分比误差yMAPE和均方根误差yRMSE两项指标来评估预测模型,表达式如下:
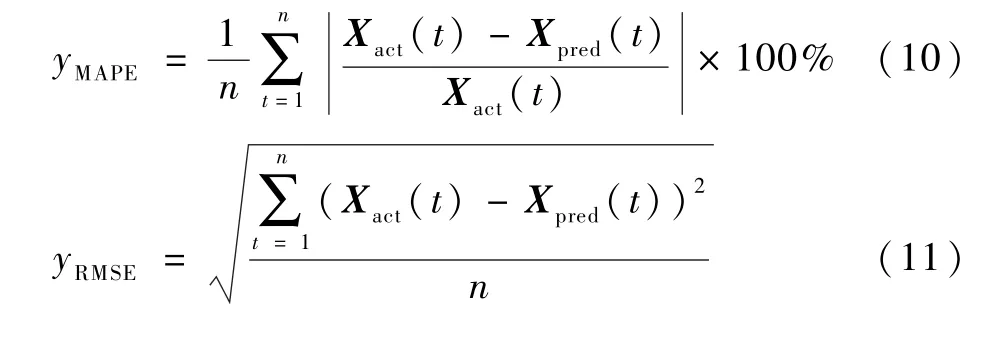
yMAPE可以评估模型精度,yRMSE可以表现预测的精度。yRMSE的数量级会跟随电力负荷值的数量级变化,是相对值指标。yMAPE和yRMSE的值越小,表明误差越小,负荷预测效果越好。
3 算例分析
3.1 数据预处理
实验基于嘉捷BOX 和重庆丽苑维景国际大酒店这2 个实际电力负荷的数据集,将所提的PCC-LSTM 与Prophet、LSTNet、门控循环(gate recurrent unit, GRU)神经网络模型方法所得结果进行对比。 Prophet 是对负荷数据进行拟合的时间序列模型[25];LSTNet 是针对多变量时间序列预测的深度学习网络,其模型综合了长期模式和短期模式[26];GRU 是基于LSTM 网络模型结构进行优化[27]。
2 个电力负荷数据集均提供了电力负荷数据、工作日信息、节假日信息、天气信息、温度数据和湿度数据,一天采集24 个点,时间间隔为1 h。以2020 年11 月的数据作为训练数据集,2020 年12 月的数据作为测试数据集。 对于存在的数据丢失问题,取附近前后各2 个相似日数据的均值进行填补;对于突然变得异常大和突然变为0 的数据,根据此数据所处时间前后时间段的数据及相似日的数据合理给出数据进行替换。 采用min-max 标准化方法将原始数据归一化到[0,1]之间。 对工作日、节假日和天气等影响因素做量化处理,如对于节假日,节假日的预测日置1,否则置0。
基于表2 的分析结果,选取3 个会对嘉捷BOX 造成明显影响的因素:湿度、工作日、温度。因此输入数据x主要由以下特征组成:历史负荷、湿度、工作日、温度。 由于待预测日的负荷数据与前一天负荷具有很大的相关性,选取前一天每小时(共24 h)的特征数据作为输入,待预测日24 h的电力负荷值为输出。

表2 嘉捷BOX 影响因素相关性分析Table 2 Correlation analysis of influencing factors of Jiajie BOX
重庆丽苑维景国际大酒店Pearson 相关性分析结果如表3 所示。 基于此分析结果,选取了1 个会对重庆丽苑维景国际大酒店造成显著影响的因素:湿度。 因此输入数据x主要由以下特征组成:历史负荷、湿度。 类似,选取前一天每小时(共24 h)的特征数据作为输入,待预测日24 h 的电力负荷值为输出。

表3 重庆丽苑维景国际大酒店影响因素相关性分析Table 3 Correlation analysis of influencing factors of Chongqing International Grand Metropark Liyuan Hotel
3.2 实验设置
实验使用的是64 位Windows10 版本系统的计算机。 在此操作系统上,利用PyCharm Professional Version 2020.3.1 和Anaconda3 开发环境,使用基于Keras 深度学习工具的Tensorflow 框架搭建模型。 Keras 库具有模块化的特点,支持神经网络层的自由组合和层层叠加。 Prophet 模型调用Facebook 开源的fbprophet 包。
3.3 嘉捷BOX 实验结果分析
PCC-LSTM 模型参数调优采用控制变量法。经实验发现,模型训练初期,预测精度随LSTM 神经网络层数的增加而提高,但当LSTM 网络层增加到3 层时预测精度降低,表示预测模型对训练数据过拟合。 因此选择LSTM 网络层数为3 层,各层神经元数量均为500,Dropout 为0. 5,在LSTM 后加入一个全连接层,神经元数量为100,迭代次数为800,学习率为0.001。
以嘉捷BOX 2020 年11 月的数据作为训练集,2020 年12 月的数据作为测试集,对测试集的电力负荷日用电量进行预测。
图3 ~图6 为PCC-LSTM 模型2020 年12 月1 日至4 日连续4 日的负荷预测结果,每1 h 为1 个时间采样点。 对PCC-LSTM 模型连续4 日的预测结果计算平均绝对百分比误差yMAPE和均方根误差yRMSE,结果如表4 所示。
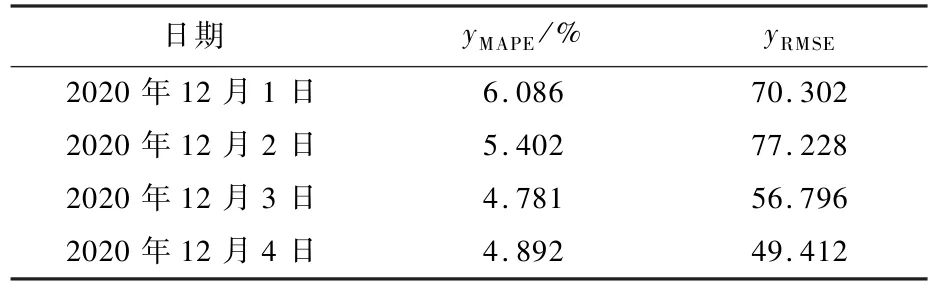
表4 嘉捷BOX PCC-LSTM 模型预测结果yMAPE 和yRMSE 对 比Table 4 Comparison of yMAPE and yRMSE of prediction results with PCC-LSTM model of Jiajie BOX
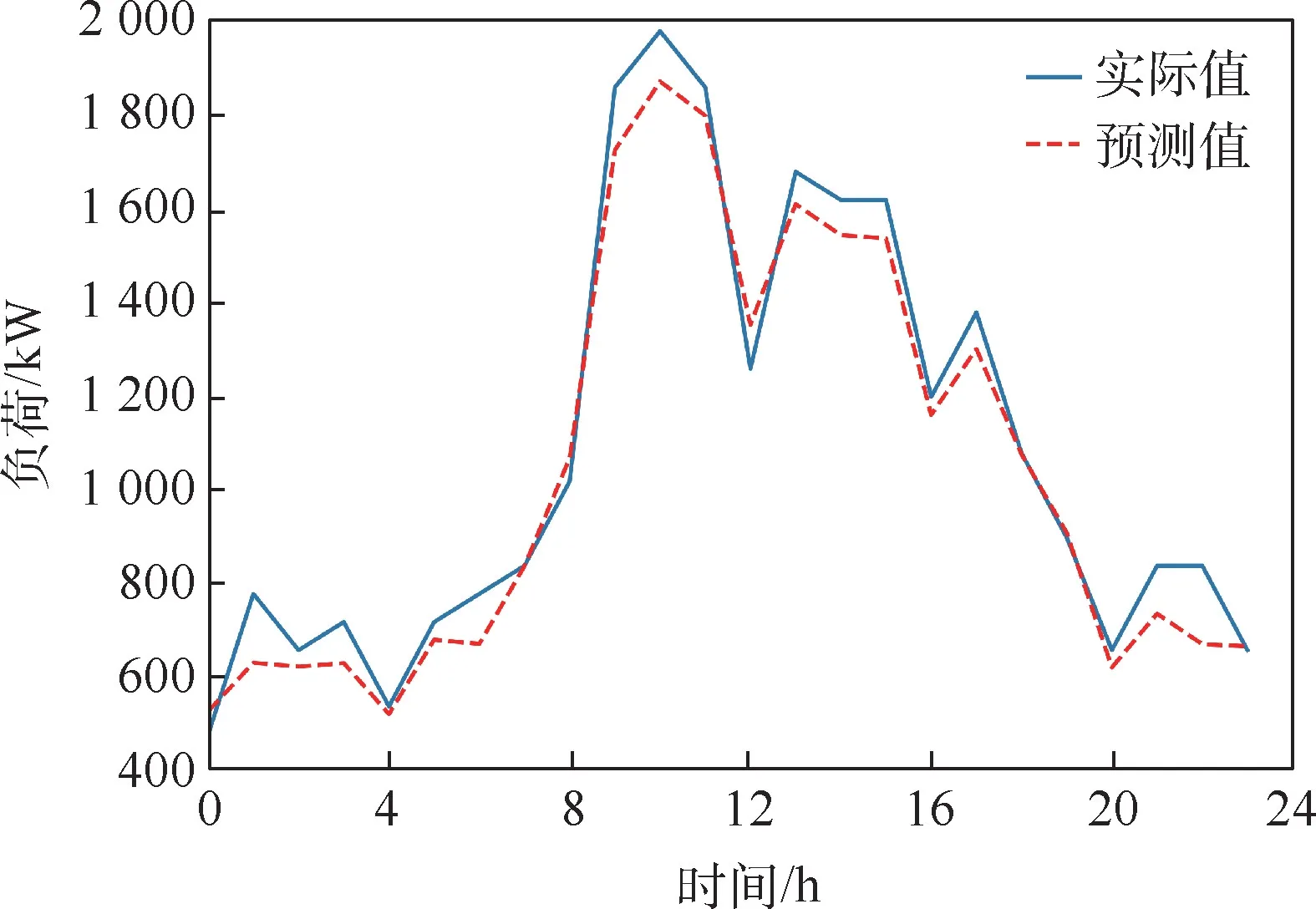
图3 嘉捷BOX PCC-LSTM 模型2020 年12 月1 日预测结果Fig.3 Predicted curve of PCC-LSTM model of Jiajie BOX on December 1, 2020
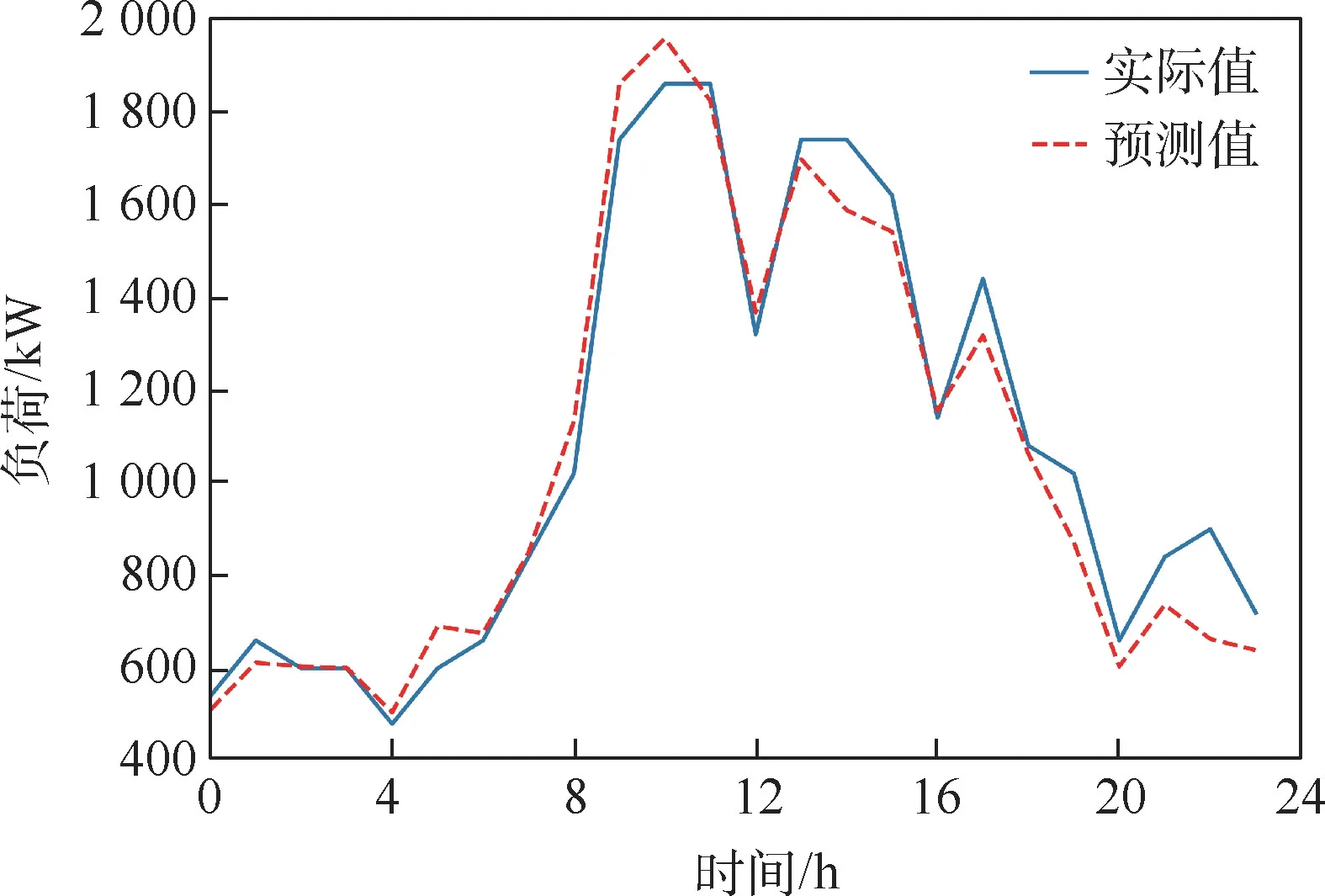
图4 嘉捷BOX PCC-LSTM 模型2020 年12 月2 日预测结果Fig.4 Predicted curve of PCC-LSTM model of Jiajie BOX on December 2, 2020
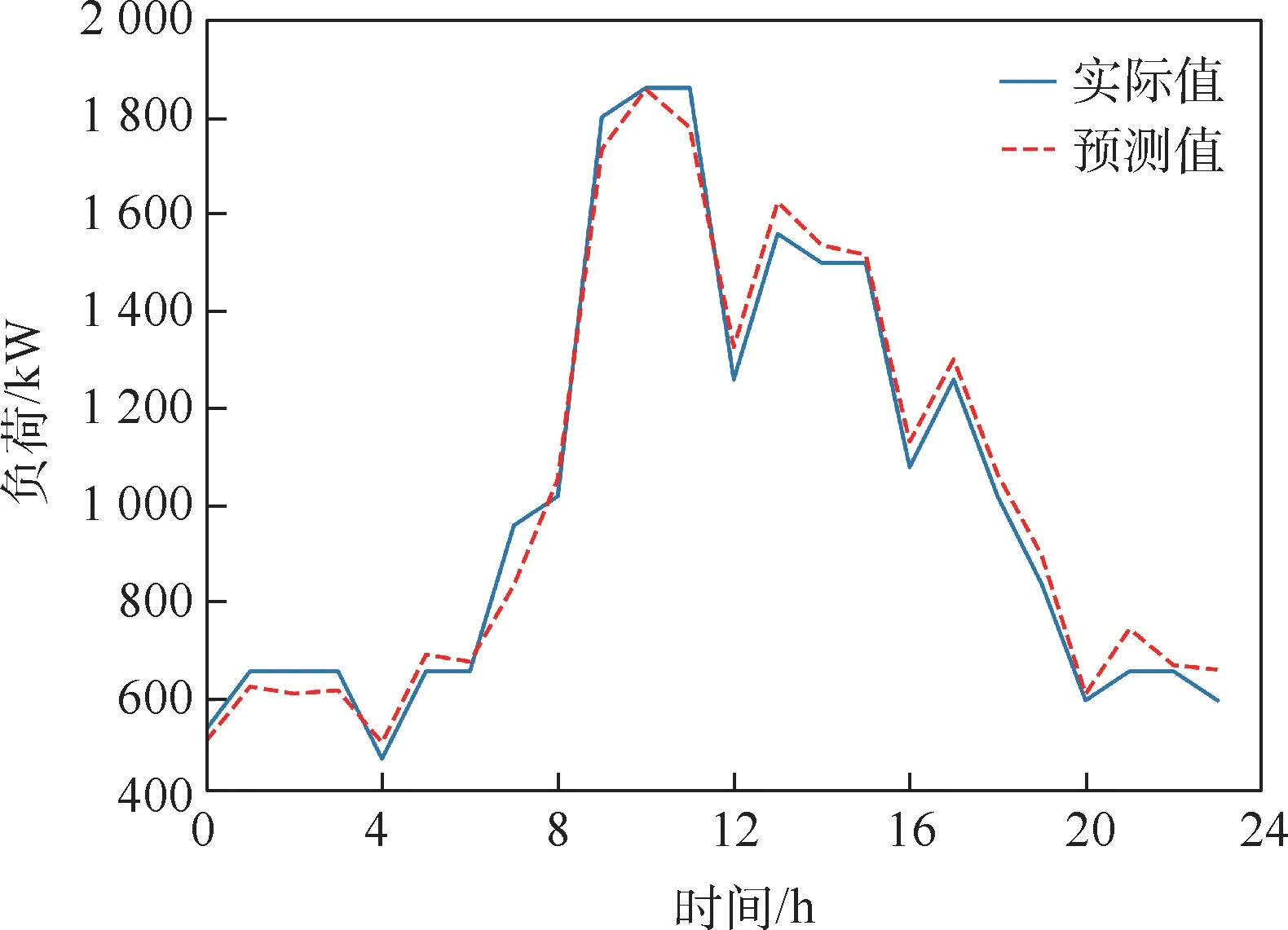
图5 嘉捷BOX PCC-LSTM 模型2020 年12 月3 日预测结果Fig.5 Predicted curve of PCC-LSTM model of Jiajie BOX on December 3, 2020

图6 嘉捷BOX PCC-LSTM 模型2020 年12 月4 日预测结果Fig.6 Predicted curve of PCC-LSTM model of Jiajie BOX on December 4, 2020
从表4 可以看出,PCC-LSTM 模型的预测误差在4.78% ~6.09%,预测精度在93.91% ~95.22%,取得了较好的预测效果。
表5 为2020 年12 月3 日的电力负荷用电量Prophet、LSTNet、GRU 和PCC-LSTM 这4 种预测模型训练结果对比。 可知,PCC-LSTM 模型的预测误差更小,预测精度更高,达到了95.44%,yMAPE相比其他3 种方法分别降低了22. 37%、6. 94%、3.02%;yRMSE分 别 降 低 了194. 93、99. 37、50. 07。PCC-LSTM 模型与其他3 种方法相比,在平均绝对百分比误差yMAPE和均方根误差yRMSE上均取得了较好的效果,预测误差更小。 同时,由表5 可以看出,Prophet 用时最短,LSTNet 用时最长,PCC-LSTM 模型用时略长于GRU,而Prophet 的高计算效率以低预测精度为代价,PCC-LSTM 模型在增加了PCC 环节提高精度的情况下,计算效率与GRU 相当。
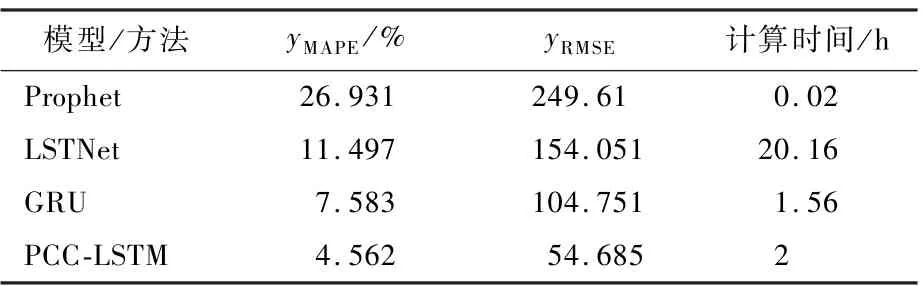
表5 不同方法嘉捷BOX 日负荷预测结果比较Table 5 Comparison of results of daily load forecasting by different methods of Jiajie BOX
嘉捷BOX 2020 年12 月3 日电力负荷用电量的实际值和4 种模型的预测结果对比如图7 所示。
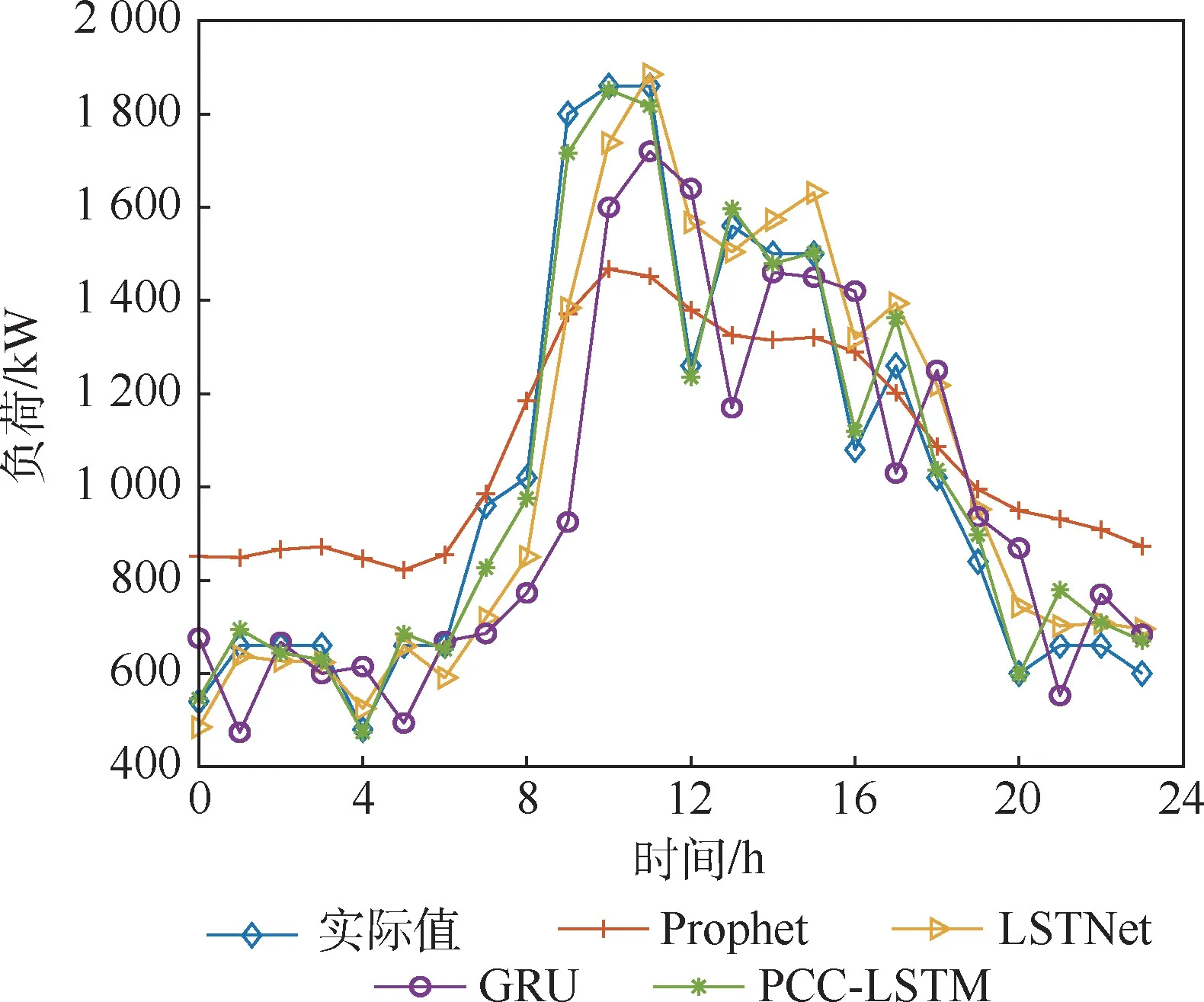
图7 嘉捷BOX 2020 年12 月3 日负荷预测结果对比Fig.7 Comparison of load forecasting results of Jiajie BOX on December 3, 2020
由图7 可知,PCC-LSTM 模型对电力负荷用电量数据进行了较好的拟合,几乎完全和电力负荷用电量实际值重合,有效预测了负荷未来用电量的变化趋势,精准地把握了负荷变化的内在规律。
3.4 重庆丽苑维景国际大酒店实验结果分析
本次实验经模型调优后,选择LSTM 网络层数为3 层,各层神经元数量均为700,Dropout 为0.5,在LSTM 后加入一层全连接层,神经元数量为100,迭代次数为700,学习率为0.001。
以重庆丽苑维景国际大酒店2020 年11 月的数据作为训练集,2020 年12 月的数据作为测试集,对测试集的电力负荷日用电量进行预测。
图8 ~图11 为PCC-LSTM 模型2020 年12 月3 日至6 日连续4 日的负荷预测结果,每1 h 为1 个时间采样点。 对模型连续4 日的预测结果计算平均绝对百分比误差yMAPE和均方根误差yRMSE,结果如表6 所示。
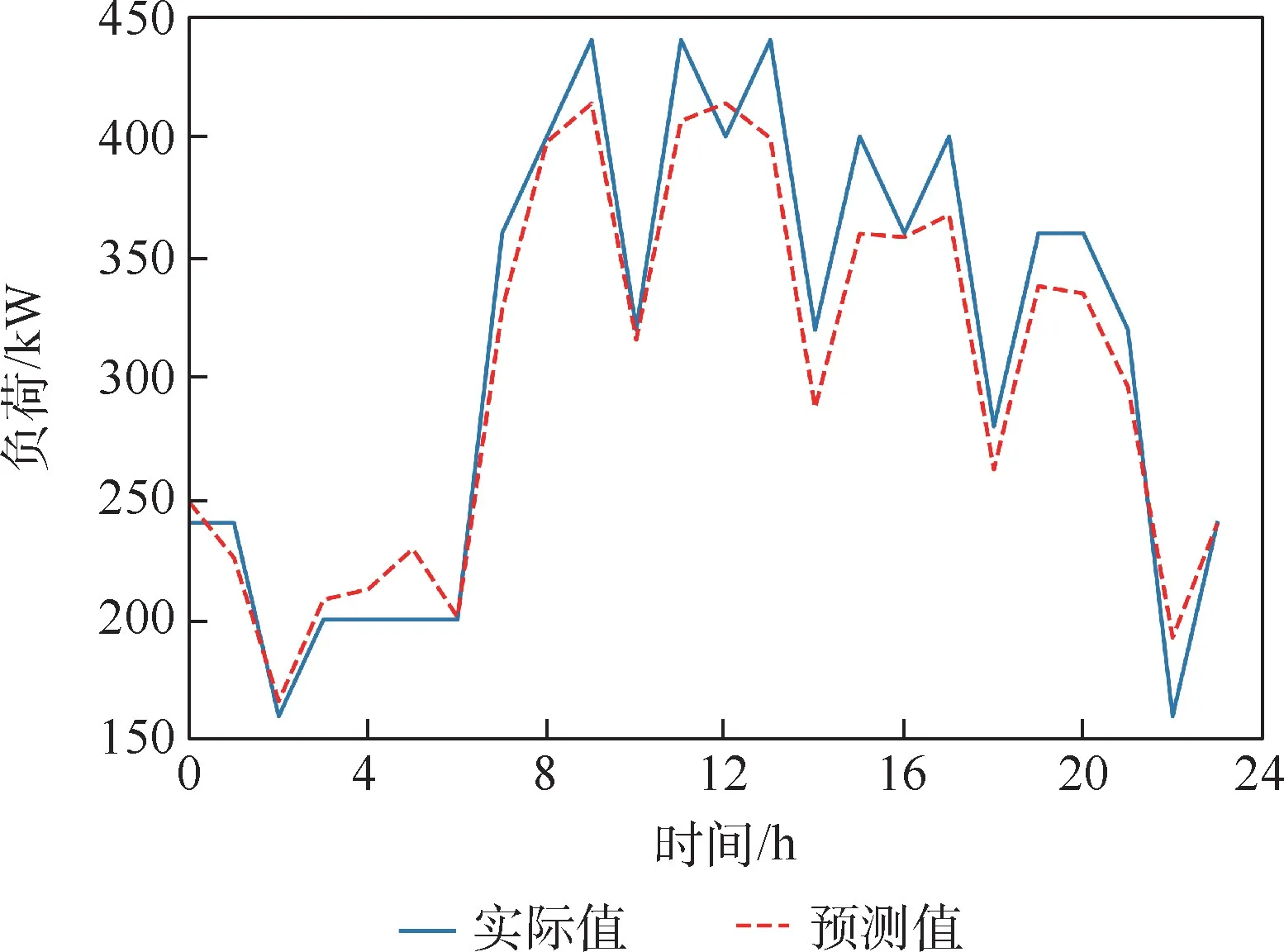
图11 重庆丽苑维景国际大酒店PCC-LSTM 模型2020 年12 月6 日预测结果Fig.11 Predicted curve of PCC-LSTM model of Chongqing International Grand Metropark Liyuan Hotel on December 6, 2020
从表6 可以看出,PCC-LSTM 模型的预测误差在4.76%~8.05%,预测精度在91.95%~95.24%,预测精度良好。
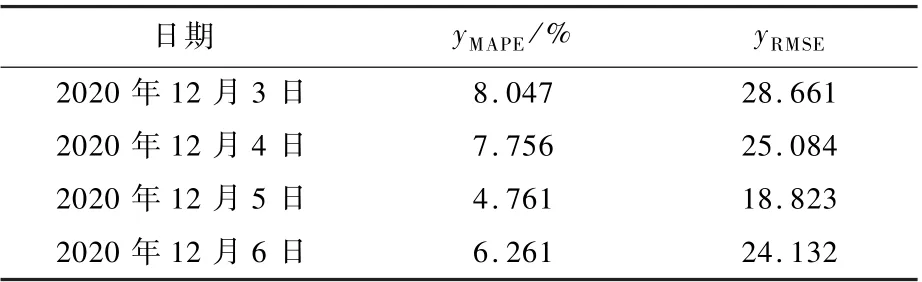
表6 重庆丽苑维景国际大酒店PCC-LSTM 模型预测结果yMAPE 和yRMSE 对比Table 6 Comparison of yMAPE and yRMSE of prediction results with PCC-LSTM model of Chongqing International Grand Metropark Liyuan Hotel
表7 为2020 年12 月5 日的日负荷Prophet、LSTNet、GRU 和PCC-LSTM 这4 种预测模型结果对比,经计算可知PCC-LSTM 模型的预测精度达到了95.13%,yMAPE相比其他3 种方法分别降低了8.16%、13.82%、0.2%、yRMSE分别降低了29.27、40.67、2.76。 PCC-LSTM 模型相对于其他3 种方法在2 项精度指标上表现更为优异。 计算时间由短到长排序为:Prophet、GRU、PCC-LSTM、LSTNet,可见PCC-LSTM 模型在提高精度的基础上,计算效率与GRU 方法相当。
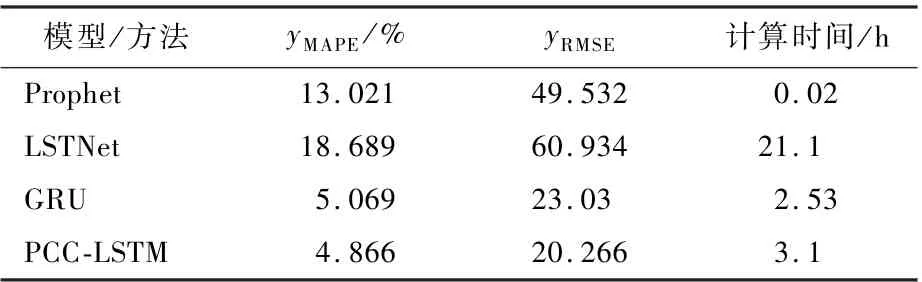
表7 不同方法重庆丽苑维景国际大酒店日负荷预测结果比较Table 7 Comparison of results of daily load forecasting by different methods of Chongqing International Grand Metropark Liyuan Hotel
重庆丽苑维景国际大酒店2020 年12 月5 日电力负荷用电量实际值和4 种模型的预测结果对比如图12 所示。 可知,PCC-LSTM 模型在重庆丽苑维景国际大酒店电力负荷用电量变化的4 个峰谷期均取得了较好的预测效果,更准确地学习了负荷变化的规律,贴近负荷实际值曲线。

图12 重庆丽苑维景国际大酒店2020 年12 月5 日负荷预测结果对比Fig.12 Comparison of load forecasting results of Chongqing International Grand Metropark Liyuan Hotel on December 5, 2020
4 结 论
本文提出了基于PCC-LSTM 模型的短期负荷预测方法,包括对PCC-LSTM 模型的训练、预测及调参等内容。 以嘉捷BOX 和重庆丽苑维景国际大酒店的电力负荷用电量数据作为实际算例,得出以下结论:
1) 与时间序列模型(Prophet) 相比,PCCLSTM 模型由于考虑了与电力负荷相关的其他影响因素,对输入量进行了更为细致的分析,有效提高了预测精度。
2) 与其他类型的神经网络(LSTNet、GRU)相比,由于PCC-LSTM 模型在输入量的选择上,采用Pearson 相关性分析选取合适的影响因素作为输入变量,提升了输入变量与目标变量的相关性,并结合LSTM 神经网络,充分挖掘时序数据间的内在关系,使得模型的拟合和预测性能整体更好。
3) PCC-LSTM 模型的预测精度对Dropout 的取值较为敏感,Dropout 取值过低,模型对训练数据过度学习,可能导致过拟合,Dropout 取值过高,模型对训练数据学习不足,可能导致欠拟合,影响模型的性能。
值得说明的是,本文使用深度学习对短期电力负荷用电量进行预测,未来可以考虑组合其他预测方法,对模型输入量和模型架构进行更为详细的划分与分析,进一步提高短期负荷预测精度。
