基于特征融合与抗遮挡的卫星视频目标跟踪方法
2023-01-12刘耀胜廖育荣林存宝李兆铭杨新岩
刘耀胜, 廖育荣, 林存宝,*, 李兆铭, 杨新岩
(1. 航天工程大学 研究生院, 北京 101416; 2. 航天工程大学 电子与光学工程系, 北京 101416)
近年来,随着科技的发展,目标跟踪技术已经成为计算机视觉的重要研究课题,在人工智能、无人驾驶、人机交互及军事监控等方面应用十分广泛[1],其主要作用是在已获得的视频图像中寻找感兴趣的目标,并且在下一帧中对其进行精确地跟踪。 目前,随着遥感技术的日趋成熟,各国遥感卫星的数量也越来越多,并且遥感卫星拍摄的高分辨率视频能够观测和测量地球表面上的移动物体,提供丰富的信息进行分析决策,如石油储量、自然灾害的监测[2],交通状况及生态系统干扰的监测[3]等。 高分辨率视频卫星作为一种新型的对地观测卫星,与传统的观测卫星相比较,其最大的优势是采用“凝视”[4]的成像模式对某个区域进行连续观察,并且以视频成像的方式获得丰富的信息,实现对卫星视频中目标持续跟踪的能力,从而将目标跟踪技术应用到遥感卫星领域。
目前,各国已经陆续发射多颗高分辨率视频卫星。 例如,2007 年印度尼西亚将“印度尼西亚国家航空航天研究所-柏林技术大学卫星”送入太空,2013 年美国的Skybox 公司成功发射2 颗视频卫星,而中国在2014 年成功将自主研制的“天拓二号”卫星发射升空,在2015 年中国长光卫星技术股份有限公司将研制的“吉林一号”视频卫星顺利升空。 由于视频卫星拍摄的图像幅宽较大,空中环境复杂,并且容易受到相似目标的干扰,以及存在目标被遮挡等问题,对卫星视频中的目标进行跟踪存在较大的挑战,以往的目标跟踪算法几乎都是对地面上的目标进行跟踪,对卫星视频中的目标进行跟踪将会成为一个新的热点问题。
针对卫星视频中的目标跟踪,一般通过目标检测获得初始帧目标的位置信息,或在初始帧手动获得目标的相关信息,再在每一帧估计所跟踪目标的位置。 近年来,在目标跟踪领域产生了多种性能优异的算法。 Bolme 等[5]首次将相关滤波的思想应用到目标跟踪领域,提出了一种基于最小误差输出平方和(minimum output sum of squared error, MOSSE)的滤波跟踪器。 之后,Henriques等[6]基于相关滤波的思想,发展设计了循环核结构(circulant structure kernel, CSK)的跟踪器和核相关滤波(kernelized correlation filters, KCF)跟踪器[7],提高了目标跟踪的速度和准确率。 杜博等[8]通过将三帧差法和KCF 算法相结合,提出了一种新的卫星目标跟踪方法。 轩诗宇等[9]将运动估计的方法和KCF 算法相融合,以解决卫星视频中目标无法进行快速跟踪的问题。 而随着深度学习的兴起,尤其是卷积神经网络(convolutional neural network, CNN)在视觉跟踪中的广泛应用,研究人员开始探索使用CNN 提取卫星视频中目标的特征,增强对目标的表示能力,提高目标跟踪的准确度。 胡兆鹏等[10]提出将简单的回归模型与卷积层和梯度下降算法相结合,利用丰富的背景知识构建强大的目标跟踪器。 邵佳等[11]提出一种用于卫星视频跟踪的预测注意启发式Siamese 网络(PASiam), 该网络提取目标的浅层特征,采用高斯混合模型检测目标的运动状态,并且使用卡尔曼滤波预测和校正目标的位置。 马成洋等[12]通过对颜色特征和方向梯度直方图(histogram of oriented gradient, HOG)特征进行融合,弥补了目标在光照变化和形变情况下的特征表示缺陷,可以在目标轻微遮挡时对目标进行跟踪。Heimbach 等[13]通过特征响应调整卡尔曼滤波器中的协方差参数,从而提高在目标遮挡情况下跟踪的准确性。 杨剑锋等[14]通过引入块均值漂移算法跟踪部分遮挡的目标,提高算法抵抗目标遮挡的能力。
然而,以上方法通常提取目标有限的特征进行表述,当目标发生光照变化或进入复杂环境中时,跟踪模型通常会产生较大的误差,从而影响跟踪器的鲁棒性。 而基于深度学习的算法虽然对目标跟踪的效果较好,但在利用CNN 等网络提取目标特征时,一般需要较大的计算量,对跟踪算法整体的实时性上受到了不利的影响。 上述目标跟踪算法在传统的图像上具有不错的跟踪精度和鲁棒性,但是在应用于卫星视频中的目标跟踪时仍存在较大问题,尤其是当目标出现遮挡、复杂背景及发生光照变化等情况时,将会发生目标跟踪丢失的问题,最终导致跟踪失败。
为确保目标跟踪具有较高的稳健性和准确性,同时也考虑到目标跟踪的精度和速度,本文采用KCF 算法作为基础目标跟踪框架,同时考虑到单一的目标特征无法较为准确地对目标进行描述,设计了一种特征自适应融合和模型自适应更新的方法。 根据响应区域的最大值和平均峰值相关能量获得权重,进行自适应特征融合,提高对单一目标特征的描述能力;采用自适应更新的方法对相关滤波模型进行更新,使相关滤波模型能够克服目标因光照变化等影响而产生的微小变化;借助卡尔曼滤波的方法预测遮挡目标在下一帧的位置,从而解决由于目标被遮挡而造成的目标跟踪失败的问题。
1 本文算法
1.1 KCF 算法
KCF 算法[7]属于判别式目标跟踪算法,将目标及周围的矩形区域作为训练样本,通过循环矩阵构造大量的正负样本,以此增强分类器的训练效果。 同时利用循环矩阵对角化的性质,将训练样本进行对角化,以此减少计算量,使用岭回归函数对样本进行分类,并对其进行约束优化获得最终的分类器。 具体步骤如下:
假设目标的训练样本为xi,用yi表示目标的高斯函数响应,采用岭回归函数并引入高斯核函数对大量样本进行训练,寻找一个合适的w,使得函数f(xi) =wTxi和高斯函数响应yi之间的平方误差和最小,即
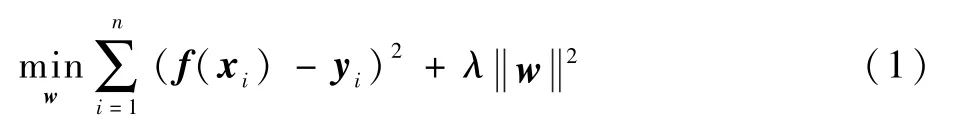
式中:λ为正则化参数,目的是防止过度拟合。
将式(1)转换成矩阵形式并求导,可得分类器权重系数w的最优解,即

假设目标样本x为n×1 的基本向量,可以表示为x=[x1,x2,…,xn],将其通过循环矩阵进行移位,从而获得大量的训练样本。 循环矩阵如下所示:
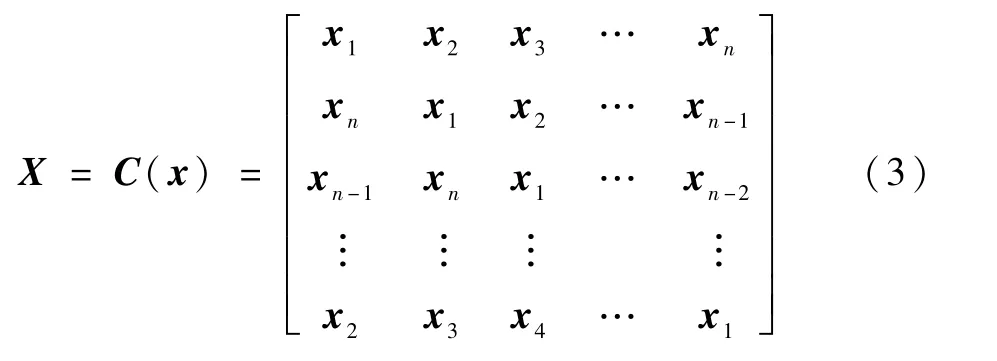
式中:第1 行为目标样本,其他行都由第1 行循环移位而来,因此可得到样本循环具有周期性。 利用循环矩阵对角化的性质,将训练样本X进行离散傅里叶变换可得

式中:“⊙”表示矩阵与矩阵之间点积。
由于样本在低维空间通常难以进行线性分类,需要将样本转化到高维空间,本文结合核函数k(x,z′)= 〈φT(x),φ(z′)〉, 目标样本的线性函数可以表示为

因此可得
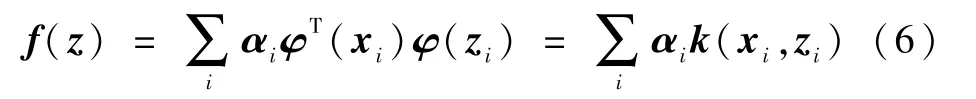
式中:k(xi,zi)为核函数;αi为滤波系数。
本文选择高斯核函数,该函数可以表示为
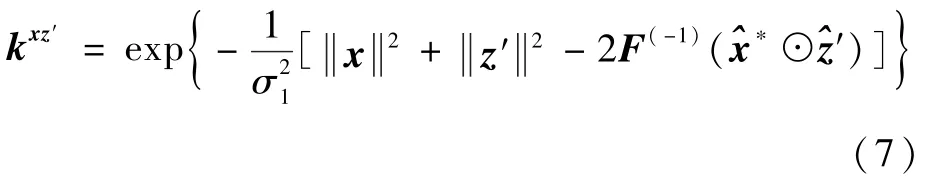
式中:z′表示待检测的图像块;F(-1)表示离散傅里叶逆变换;σ1为高斯核函数的带宽。
因此,式(4)可以转换为

式中:^y表示高斯函数y的傅里叶变换;^α表示滤波器模型。
在下一帧图像中,获取与前一帧目标大小相同的矩形区域z,可得下一帧目标的响应区域为

本文目标跟踪算法主要是对KCF 算法的改进,具体表现在特征提取、自适应特征融合、自适应模型更新及解决目标遮挡的问题。
1.2 提取的目标梯度纹理特征
在目标跟踪算法中,提取的目标特征是否有效直接决定跟踪效果的好坏。 为提高目标跟踪的效果,本文提出一种自适应融合目标特征表示方法,通过提取目标的HOG 特征[15]、灰度特征及基于高斯曲率和平均曲率的特征[16],并分析比较各种特征对目标的描述能力,从而选择合适的方法对目标进行特征融合。 因HOG 特征和灰度特征已在相关文献中有所阐述,本文不再赘述。 重点对基于高斯曲率和平均曲率的特征[16]提取方法进行介绍。
在进行目标特征描述时,由于梯度可有效描述图像像素的方向信息,被广泛用于描述目标的特征,如HOG 特征、Sobel 特征等。 然而,由于梯度信息一般仅能够反映目标边缘变化剧烈的程度,而对图像中曲率等非线性特征的描述存在一定难度,本文提出采用高斯函数来计算目标的高斯曲率特征和平均曲率特征,从而获得包括梯度纹理特征在内的更为充分的特征描述。
通过高斯函数对图像进行卷积运算通常可以获得更加突出的纹理和强度信息,因此高斯导数滤波器通常被用来作为提取纹理特征的基本模型。 高斯函数可以表示为

式中:x、y分别为图像像素的横、纵坐标;σ2为高斯函数的带宽。
本文使用高斯函数的一阶和二阶偏导数与图像I进行卷积,从而获得图像的部分特征信息。公式如下:

式中:Gx、Gy、Gxx、Gyy、Gxy分别为高斯函数对x的一阶偏导数、对y的一阶偏导数、对x的二阶偏导数、对y的二阶偏导数、对xy的二阶偏导数;“*”表示对图像进行卷积操作。
将图像所有像素由二维空间转到三维空间,通常可以得到一个三维曲面。 为体现图像的局部性质,可以通过计算图像三维曲面的平均曲率,从而获得图像的局部特征。 但是,当图像中的边缘发生距离变化时,通过平均曲率提取目标的局部特征就会存在较大误差,此时可以使用具有旋转不变性的高斯曲率特征获得图像中边缘变化剧烈的信息,从而提取目标更加详细的纹理特征。 图像的高斯曲率公式可以表示为

平均曲率公式为
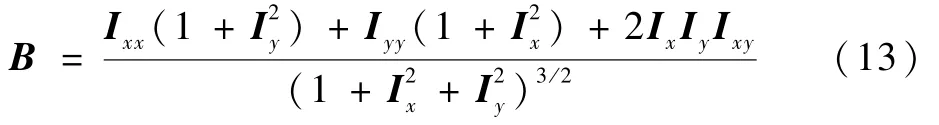
因此,图像的梯度纹理特征E可以由式(14)计算:

式中:ρ为权重,设置为0.5。
通过对图像的梯度纹理特征分析,可以检测到图像中相邻像素的显著特征。
1.3 自适应特征融合
为了提高目标跟踪的准确率,将目标的梯度纹理特征和灰度特征进行并联融合得到特征MIX,再将HOG 特征和MIX 特征分别训练KCF滤波器,从而获得最终的目标响应图,即

最终响应图f(z)可由2 个特征的响应图进行加权得到,即
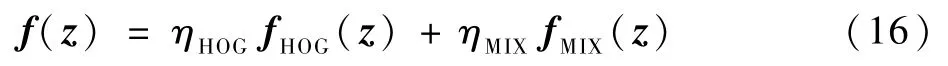
式中:ηHOG、ηMIX为融合权重。
本文将基于响应图的最大值和平均峰值相关能量(APCE)计算融合权重。 其中,APCE 定义为
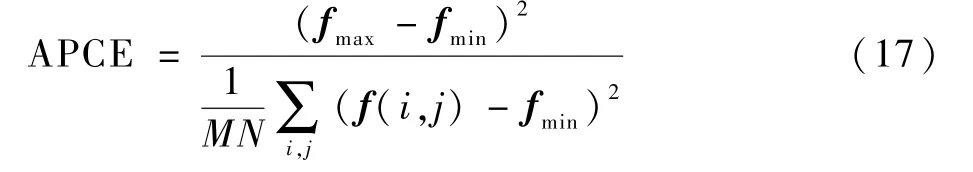
式中:fmax和fmin分别为响应图中的最大值和最小值;f(i,j)为响应图中的值;M和N分别为响应图的宽和高。
取响应图的最大值fmax和APCE 值,则结果fMA由式(18)可得

将其进行归一化,即通过将之前所有帧的fMA之和求均值,可得到最终的权重计算公式为
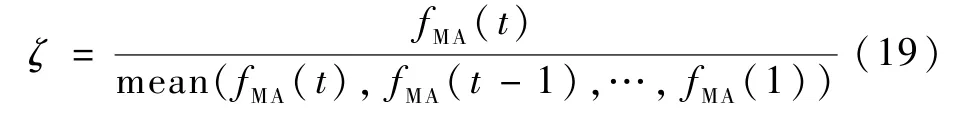
最终,HOG 特征和MIX 特征的权重ζHOG和ζMIX可以定义为

通过自适应特征融合构建稳健性的目标外观,并且特征互补可以提高目标跟踪的准确度。
1.4 自适应模型更新
在目标跟踪的过程中,由于目标和背景随时都会发生变化,滤波器的模型和目标的特征要及时进行更新,才能适应这种变化[17]。 本文提出一种新的方法对目标的模型进行自适应更新,当前帧的融合响应图中最大值与之前所有帧融合后响应图中最大值之和的均值之比定义为θ,θ可以表示为
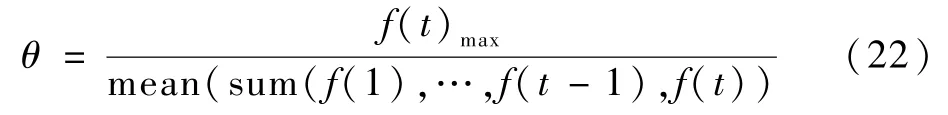
式中:t为帧的索引;f(t)max为响应最大值。
由于相关滤波器的模型是由线性插值而得的,可以将其做出如下改进,具体如下:
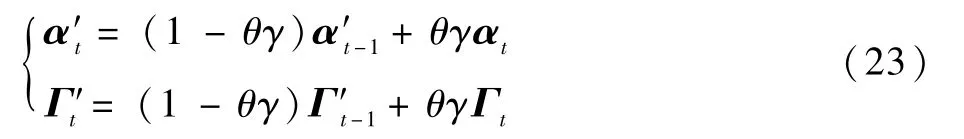
式中:α′t-1和αt分别表示第t-1 帧的滤波器模型和第t帧的滤波器模型;α′t表示经过线性插值后的滤波器模型;Γ′t-1和Γt分别表示第t-1 帧的目标特征和第t帧的目标特征;Γ′t表示经过线性插值后的目标特征;γ为初始的学习率,设为0.012。
1.5 目标遮挡的解决方法
目标遮挡处理一直是目标跟踪的难点问题。当目标被遮挡时,目标的外观模型会发生变化,而跟踪器由于无法进行判断,通常会将错误的模型进行学习,从而丢失真正的目标,最终导致目标跟踪失败。 卡尔曼滤波[18]通过输入观测数据,经过最优估计方法最终获得相对准确的结果。 通过对卫星视频目标跟踪问题的分析,本文提出引入卡尔曼滤波算法解决目标遮挡问题,通过响应图的APCE 值判断目标是否被遮挡,从而决定是否使用卡尔曼滤波算法对遮挡目标进行位置预测。
卫星视频中典型的运动目标是车辆、舰船和飞机,当目标处于转弯、紧急停止时[9],可以假设目标在短时间内均匀的运动。 卡尔曼滤波算法的时间更新方程为

式中:xk-1为k-1 时刻的状态估计值;C为控制矩阵;uk-1为控制增益,可以设置为0;A为状态转移矩阵;xk为k时刻的状态估计值,所选择的状态量xk= [Lx,Ly,Vx,Vy],(Lx,Ly) 表示第k时刻目标中心位置点的横、纵坐标,(Vx,Vy)表示第k时刻目标在水平方向和竖直方向的速度大小;Pk-1为第k-1 时刻的状态估计协方差;Q为过程噪声的协方差。
卡尔曼滤波状态更新方程可以表示为
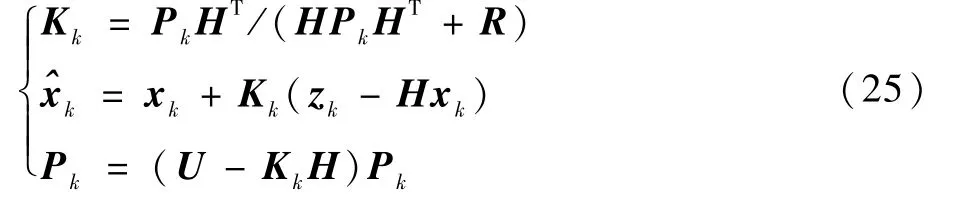
式中:Kk为卡尔曼增益;zk表示前一时刻的目标测量结果;H为测量矩阵;R为测量噪声矩阵;U为单位矩阵。
在本文中,设zk= [Px,Py],Px、Py分别表示目标中心位置的横、纵坐标,测量噪声R值很小,可以设为R=10-6I2×2。 而过程噪声Q值较大,可设为0.1I4×4。 其他参数可以定义为
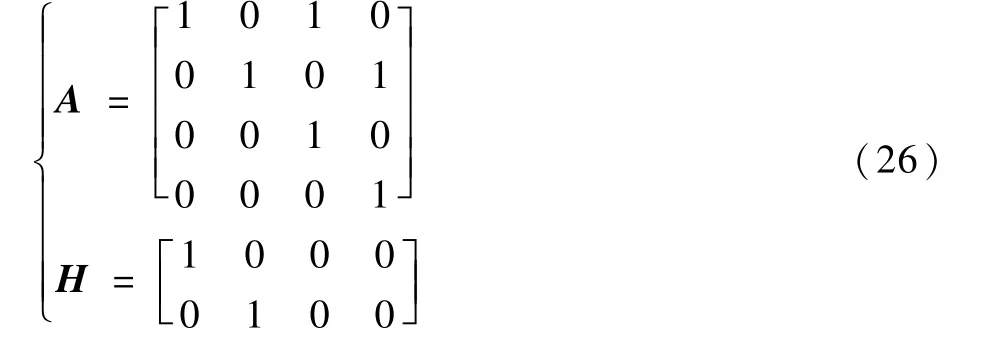
通过引入卡尔曼滤波算法可以预测遮挡目标的位置,能够进行实时地跟踪,从而解决目标被遮挡的问题。 经过多次实验证明,该方法极大地提高了目标跟踪的成功率。 算法流程如图1所示。
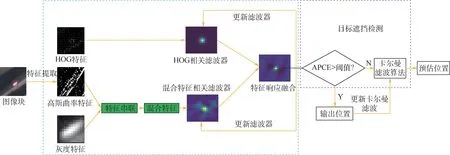
图1 基于改进的相关滤波卫星视频目标跟踪算法流程Fig.1 Flowchart of target tracking algorithm in satellite videos based on improved correlation filter
2 仿真实验结果与分析
2.1 仿真实验环境及参数
本文实验环境如下:Win10 系统,处理器Intel Xeon CPU E3-1240(3.50 GHz),16 GB 内存,仿真环境为Python 3.7。 为体现算法的一致性,设置的参数与原始KCF 算法的参数基本相同。 HOG特征的胞元大小为4 像素×4 像素,直方图方向设置为9 个,搜索区域为原始矩形框区域的1.5 倍,正则化参数为0.000 1。 卫星视频为“吉林一号”卫星数据,选取4 个具有代表性的卫星视频,包含空中飞机、地面车辆和海面舰船目标。每个视频约为300 帧,采用手动标记确定目标真实边界框。
2.2 评价方法
为定量分析本文改进算法对卫星视频中目标跟踪的性能,选取中心位置误差(center location error, CLE)、距离精度(distance precision, DP)、重叠率(overlap precision, OP)[19]作为算法性能评价指标。 中心位置误差定义为

式中:(xi,yi)为由跟踪器计算所得的目标中心位置;(xi-gt,yi-gt)为目标的实际中心位置。 CLE 值越小,说明目标跟踪的精度就越高。
距离精度定义为
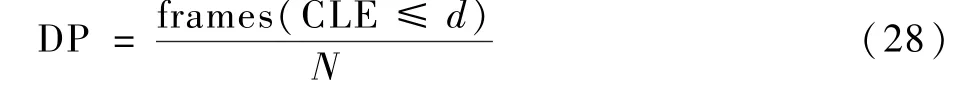
式中:frames(a)表示满足条件a的帧数;N为图像的总帧数。 由于卫星视频中目标比较小,阈值d=3。
重叠率定义为

式中:Si和Si-gt分别表示第i帧的图像边界框和手工标记的边界框;“∪”和“∩”分别表示并集和交集。 重叠率表示重叠面积占2 个边界框面积之和的百分比小于或等于阈值τ的帧数占总帧数的百分比,阈值τ设为0.75,重叠率越大,说明目标跟踪的成功率就越高。
2.3 实验过程分析
选用几种经典的算法进行对比,分别为原始的KCF 算法[7]、CSK 算法[6]、MOSSE 算法[5]、MIL算法[20]、TLD 算法[21]和MEDIANFLOW 算法[22]。MOSSE 算法首次将相关滤波的思想应用到目标跟踪领域的算法;CSK 算法通过循环矩阵构建大量样本,并且将核函数应用到目标跟踪领域;KCF算法提取目标的多通道特征,即HOG 特征,同时使用不同的核函数;TLD 算法和MEDIANFLOW算法都基于光流法对目标进行跟踪,且TLD 算法通过对目标进行重新检测,防止目标丢失或者发生漂移,从而提高目标的成功率。
由于遥感图像的幅宽较大,本文通过截取目标跟踪的局部区域进行算法验证。 图2 ~图5 为目标跟踪的精度和成功率曲线,图6 为实验的4组卫星视频图像,图7 为目标跟踪结果的部分可视化图像。 图7 中:左上角数字表示视频图像的帧数,蓝色框表示目标的运动区域,其他矩形框表示目标跟踪算法的跟踪结果。

图2 空中目标跟踪结果的精度和成功率曲线Fig.2 Precision and success curves of target tracking results in Plane sequences
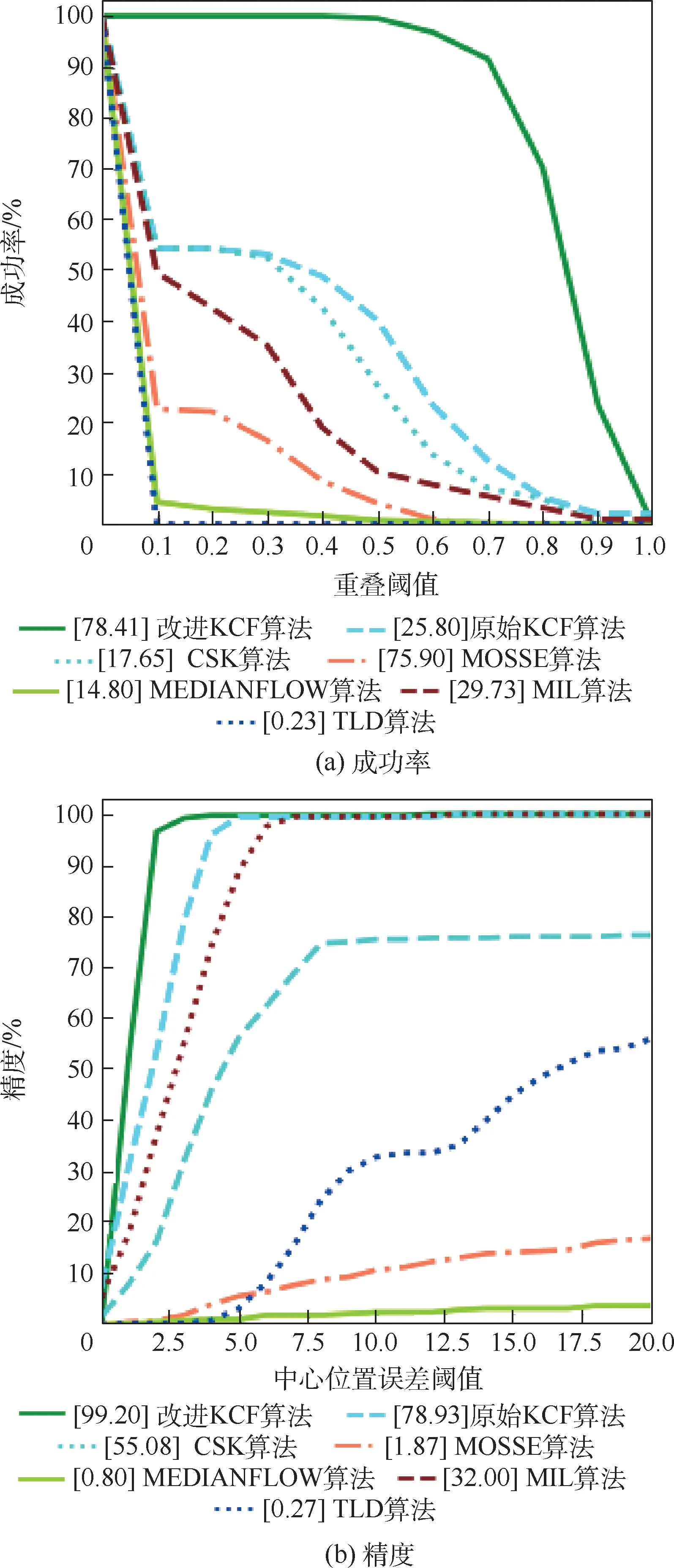
图3 遮挡目标跟踪结果的精度和成功率曲线Fig.3 Precision and success curves of occluded target tracking results in Car1 sequences
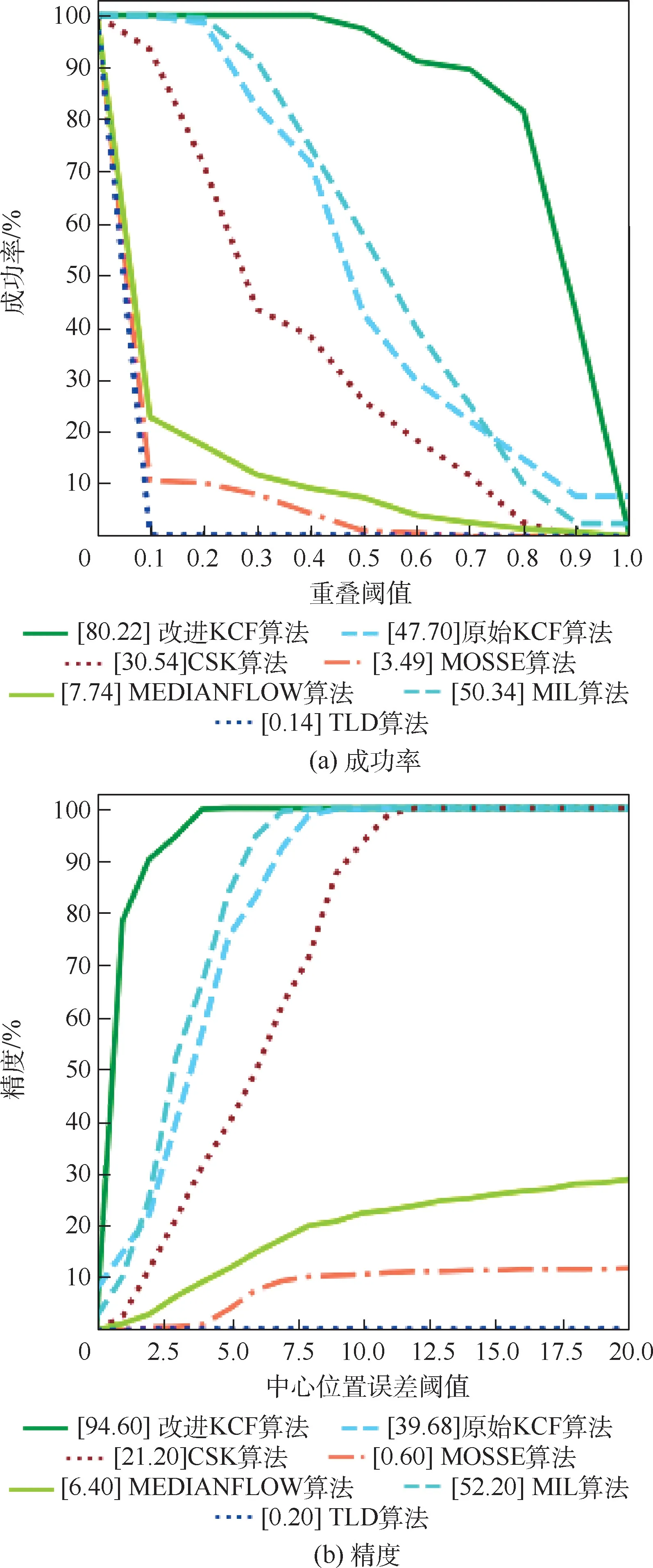
图4 运动目标跟踪结果的精度和成功率曲线Fig.4 Precision and success curves of target tracking results in Car2 sequences
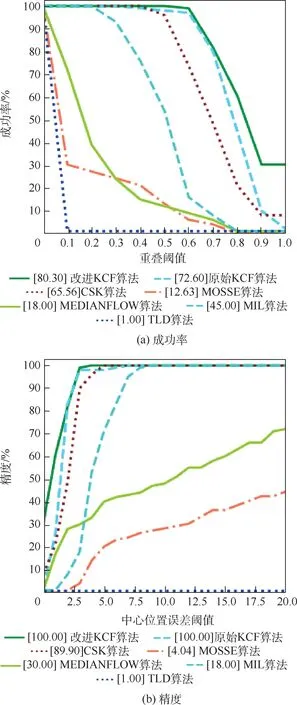
图5 海面目标跟踪结果的精度和成功率曲线Fig.5 Precision and success curves of target tracking results in Ship sequences

图6 卫星视频的运动目标及运动区域Fig.6 Moving target and moving area of satellite videos

图7 目标的可视化跟踪结果Fig.7 Visualization tracking results of targets
对空中目标(Plane)进行跟踪,从跟踪结果分析可得,图5 的精度曲线和成功率曲线及表1 表明,本文算法与其他几种算法相比,成功率和精度都有较大提高,与原始KCF 算法比较,提高了30%和21%。 曲线下面积(AUC)也作为一个跟踪算法性能的评价指标。 说明本文算法具有良好的鲁棒性,取得不错的跟踪效果。 从图7 中Plane 视频序列图像也可以看出,不同算法对目标跟踪的结果不同,对目标进行跟踪时,原始KCF 算法和CSK 算法的跟踪结果与改进KCF算法跟踪结果相差不大,但随着目标的运动,导致各种算法的误差累积越来越大。 从最终结果可以看出,本文算法对空中目标进行跟踪具有不错的效果。
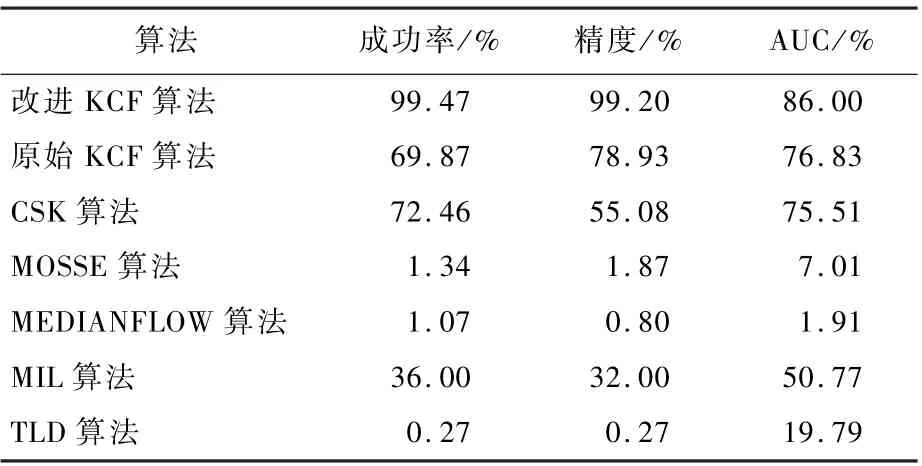
表1 Plane 视频序列中目标跟踪结果Table 1 Target tracking results in Plane video sequences
对遮挡目标(Car1)进行跟踪,从跟踪结果分析得出,通过对图3 和表2 中跟踪结果的分析可得,本文算法由于引入了卡尔曼滤波,能够对遮挡目标进行较为准确的跟踪,与原始KCF 算法相比,成功率和精度提高了约80%和70%。 从图7中Car1 视频序列中可以得到,当目标在运动过程中,由于目标的尺寸较小,且被大桥遮挡造成目标丢失,最终导致目标跟踪失败。 在第48 帧时,原始KCF 算法和CSK 算法可以对未遮挡的目标进行跟踪,取得了不错的结果。 而在第225 帧时,由于前期误差的存在,部分算法跟踪的结果出现目标丢失或者漂移,而当目标被遮挡时,由于其他算法没有解决目标遮挡的能力,导致目标重新出现时,无法对目标进行重新跟踪,从而造成目标跟踪失败。 本文算法通过引入卡尔曼滤波算法,可以对遮挡的目标进行位置预测,并且设置遮挡阈值,对目标是否遮挡进行判断,如图8 所示,红色曲线表示阈值,经过多次实验,选取阈值为18,蓝色曲线表示每一帧的APCE 值,当APCE 值小于该阈值时,可以认为目标被遮挡,此时对目标进行位置预测,同时目标不进行模板更新;当APCE 值大于该阈值时,表示目标并没有被遮挡,此时对目标进行正常跟踪。 因此,可以表明本文算法对遮挡目标的跟踪也有不错的效果,从而解决目标遮挡的问题。
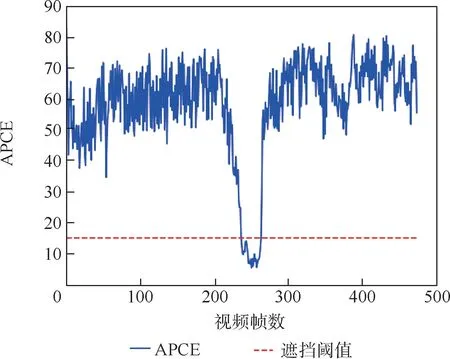
图8 APCE 值和视频帧数的关系Fig.8 Relationship between APCE values and number of video frames
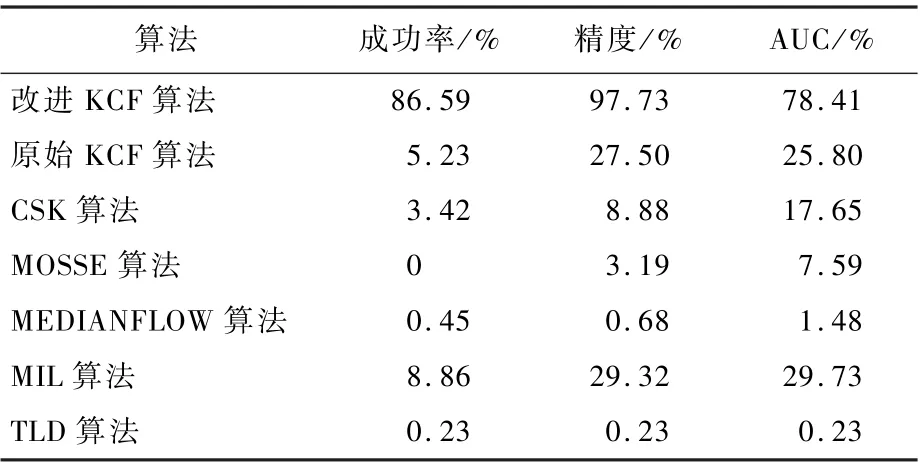
表2 Car1 视频序列中遮挡目标跟踪结果Table 2 Occluded target tracking results in Car1 video sequences
对运动目标(Car2)进行跟踪,从跟踪结果分析得到,图4 和表3 表明,改进KCF 算法可以适用于地面的目标跟踪,并且精度和成功率也有较大提高,图7 中Car2 视频序列说明了部分算法在第61 帧时对目标跟踪的结果就出现了偏差,而在第112 帧及后续出现的帧中都出现了很大的跟踪误差。 因此,这几种典型的目标跟踪算法对卫星视频中的小目标进行跟踪存在一定的困难,需要对其进行改进,可能会达到较好的跟踪效果。 而本文算法由于对原始KCF 算法进行改进,提高对目标外观的描述能力,从而提高目标的跟踪结果。
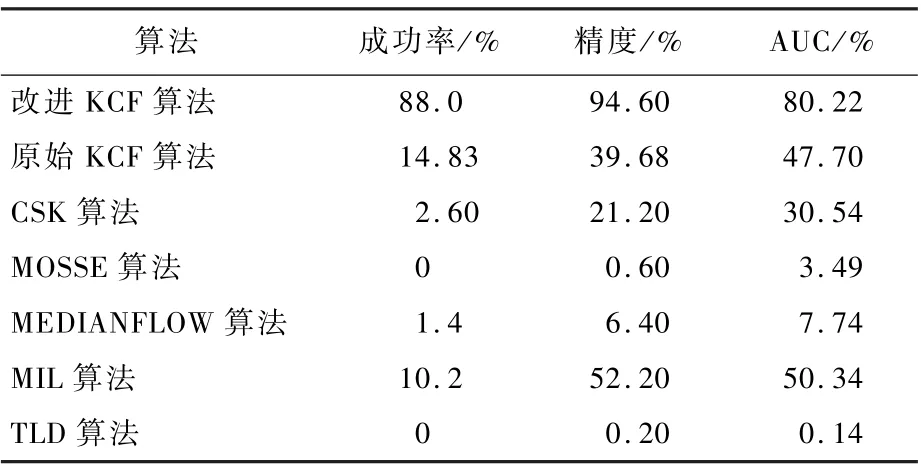
表3 Car2 视频序列中目标跟踪结果Table 3 Target tracking results in Car2 video sequences
对海面舰船(Ship)目标进行跟踪,并对跟踪结果分析可得,从图5 和表4 可以得出,本文算法比原始KCF 算法在成功率方面提高了约20%,而在精度方面并没有提高,但这并不能表示本文算法没有效果,而恰恰说明原始KCF 算法可以对船只进行跟踪也达到了较好的跟踪效果,但从成功率和AUC 来说,本文算法比原始KCF 算法效果相比,具有较好的跟踪效果。 从图7 中Ship 视频序列中可以看出,船只在运动过程中,由于产生很多的波浪,对目标跟踪存在一定的干扰,有可能造成跟踪器对目标误判。 而KCF 算法由于提取的是目标的HOG 多通道特征,可以对目标进行描述,而本文通过将灰度特征和高斯平均曲率特征融合在一起,进行自适应特征融合,从而对目标的外观进行较为详细的描述,提高目标跟踪的成功率。
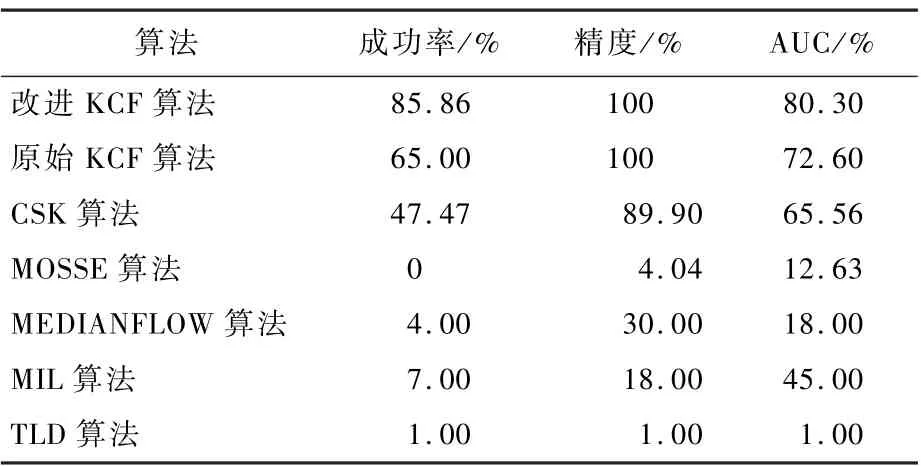
表4 Ship 视频序列中目标跟踪结果Table 4 Target tracking results in Ship video sequences
综上,本文算法通过对卫星视频中目标进行跟踪,所获得的精度和成功率都得到极大的提高。
3 结 论
本文提出一种基于改进相关滤波的卫星视频目标跟踪算法,可以对目标进行较为准确的跟踪。
1) 通过提取目标的高斯曲率特征,作为补充特征,提高对目标外观的描述能力,经过实验表明,通过提取目标的多种特征,可有效提高目标跟踪的成功率,从而达到稳健的跟踪效果。
2) 本文算法通过设计一种自适应特征融合和自适应模型更新的方法,获得鲁棒性的特征和模型,从而提高目标跟踪的精度。
3) 本文算法通过引入卡尔曼滤波算法解决目标在运动过程中存在的遮挡问题,通过预测遮挡目标在下一帧中的位置,当遮挡结束目标重新出现时,可以对目标进行较为准确的跟踪,经过在多种卫星视频数据上进行实验验证,可以有效解决目标遮挡的问题。
实验结果表明,在相似目标干扰、目标遮挡及复杂环境下,本文算法均能够对卫星视频中的目标进行跟踪,并且具有良好的鲁棒性。 但由于本文实验只考虑了刚性目标,而未对非刚性目标进行处理,当目标发生尺度变化时,本文算法可能会跟丢目标。 因此,目标的尺度变化问题将是下一步研究的重点。
