基于改进HHT的矿山微震信号多尺度特征提取及分类研究①

2023-01-12王英乐左宇军林健云郑禄璟万入祯

矿冶工程 2022年6期

王英乐，左宇军，陈斌，林健云，郑禄璟，万入祯

（贵州大学矿业学院，贵州贵阳 550025）

微震监测是一种有效的区域性地压监测手段。由于矿山环境复杂，干扰因素较多，将有效的微震事件从众多的样本数据中提取出来是实现微震监测预警的前提［1］。微震信号是典型的非线性、非平稳信号，受复杂的背景噪声干扰，常规方法很难有效识别与提取。

目前，针对矿山岩体微震和爆破信号的识别方法主要有时频分析和多参数联合识别［2-4］。时频分析能有效提取非线性信号的波形频谱特征，文献［5-6］借助小波包变换研究了微震和爆破信号在多频带内的能量分布特征，将小波包与分形相结合提取微震信号特征，并采用支持向量机（SVM）对信号进行分类，识别率达到94%；文献［7］采用频率切片小波变换对岩体微震与爆破信号的时频特性、不同频带能量分布和相关系数进行了研究；文献［8］提出了基于经验模态分解（EMD）和奇异值分解（SVD）的矿山信号特征提取及分类方法；文献［9］在经验小波变换基础上提出一种新的频谱分割方法，通过SVD分解提取最大奇异值和奇异熵作为模式识别的特征向量；文献［10］利用局部均值分解法（LMD）对微震信号分解，并将主分量的相关系数和能谱系数作为模式识别的特征向量。

针对EMD存在的模态混叠和端点效应等问题，本文将互补集合经验模态分解（CEEMD）［11］结合Hilbert-Huang变换（HHT），提出改进HHT时频分析方法。根据相关系数和方差贡献率筛选出主要IMF分量，并采用偏度、峭度、Hilbert边际谱能量、Lempel-Ziv复杂度以及分形盒维数等5种时频域特征参数构成多尺度高维特征向量；利用文献［12］提出的拉普拉斯得分（LS）特征降维方法，选择有意义的敏感特征子集，改善分类性能；最后通过GA-SVM模型实现矿山岩体微震和爆破信号的智能识别分类。

1 基本理论

1.1 CEEMD分解原理

CEEMD分解是针对EMD分解存在的端点效应和模态混叠现象而提出的一种非线性信号分析方法。CEEMD分解由以下3个步骤组成［13］：

步骤1：在原始信号中加入n组正、负成对的辅助白噪声，从而生成两组集合信号：

式中S为原始信号；N为辅助噪声；M1和M2分别为加入正负成对噪声后的信号。这样得到集合信号的个数为2n。

步骤2：对集合中的每一个信号进行EMD分解，每个信号得到一组IMF分量，其中第i个信号的第j个IMF分量表示为xij。

步骤3：通过多分组分量组合的方式得到分解结果：

式中xj为CEEMD分解最终得到的第j个IMF分量。

其中所加白噪声的残余噪声随分解次数增加而逐渐减少，本文所选的白噪声幅值标准差是原始信号幅值标准差的0.2倍，分解次数为200次。

1.2 Hilbert变换和边际谱能量

信号x（t）进行CEEMD分解后，对相关系数较大的IMF分量imfi（t）进行Hilbert变换，可得Hilbert谱，记为［14］：

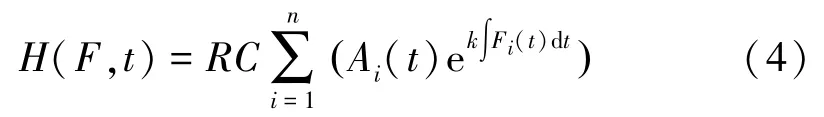
式中RC表示取实部运算；Ai（t）为瞬时幅值；Fi（t）为瞬时频率。

Hilbert边际谱h（F）定义为：

Hilbert边际谱能量E（F）定义为：

式中F1、F2分别为Hilbert边际谱h（F）的频率区间。

1.3 基于LS的特征降维

LS的思想是根据特征参数的局部保持能力来评价特征的重要性［14］。给定m个数据样本，每个数据样本包含n个特征。假设Lr为第r（r＝1，2，…，n）个特征的LS，令fn为第i（i＝1，2，…，m）个样本对应的第r个特征。

1）构建样本的最邻近图G。当两个样本xi和xj（i≠j）较“近”时，将两个样本通过边相连。可以取xi的k邻近点，建立最近邻近图。

2）计算相似度矩阵S：

式中T为合适的常数。

3）计算图的拉普拉斯矩阵L：

对于第r个特征，fr可以定义为：

式中矩阵L称为拉普拉斯变换。

第r个特征的拉普拉斯积分为：

式中Var（fr）为第r个特征对应的方差。

Sij值越大，Laplacian分数Lr越小，特征的重要性越高。选取前几个LS值较小的特征作为包含几乎全部微震信号信息的敏感特征，可提高计算效率。

2 基于改进HHT的信号特征提取

基于改进HHT的分类方法具体步骤如下：

1）将原始信号的振幅归一化处理，对其进行CEEMD分解得到数个IMF分量。

2）根据相关系数和方差贡献率，筛选包含真实信息的IMF分量，对其进行信号重构。

3）计算步骤2）中筛选出的IMF分量的峭度、偏度、边际谱能量和Lempel-Ziv复杂度以及重构信号分形盒维数，作为特征参数。

4）利用LS算法选出包含信号敏感特征的低维特征向量集。

5）根据步骤4）中的特征向量集，将训练集数据代入GA-SVM进行训练，获得C和g最优时的模型，再将测试集输入此模型进行信号分类。

3 工程实例分析

3.1 微震波形时频特征分析

从黔西南锦丰金矿的IMS微震监测系统中选取典型的微震和爆破信号，其波形和频谱如图1所示。它具有如下特点：①微震信号是岩体裂纹扩展发育中形成的，主要是剪切破坏，S波明显，波形持续时间较长且衰减缓慢。频带分布较窄，能量较为集中且主要分布在0～100 Hz。②爆破信号主要为纵波，一般有重复波形，但衰减较快，尾波不发育，且幅值通常高于微震信号；频带丰富，但能量主要集中在150～250 Hz。

图1 岩体破裂和爆破振动信号波形和频谱图

对两类信号进行CEEMD分解，得到数个从高频到低频的IMF分量。计算各分量与原信号的相关系数和方差贡献率，结果见图2，两个指标值越大，对应的分量越重要。两类信号前6个分量的相关系数和方差贡献率较大，当超过IMF6时，相关系数和方差贡献率最大值仅为0.008 7和0.000 4，可认为IMF7～IMF11在原始信号中所占比重较小，可以剔除。故选取IMF1～IMF6为主要分量进行特征提取。

图2 IMF分量相关系数和方差贡献率

3.2 基于CEEMD-Hilbert的信号特征提取

通常IMF分量包含多维信息，结合微震和爆破信号的差异特点和应用场景，本文选取信号的偏度、峭度、Lempel-Ziv复杂度、Hilbert边际谱能量、分形盒维数等参数联合组成多维特征向量。从微震监测系统中分别随机抽取200组爆破和微震信号，通过matlab编程计算前6个IMF分量和重构信号的上述特征参数，构成400×28特征向量集。

信号的偏度是描述信号幅值分布对称性的特征统计量，为无量纲参数，可以定量表征信号概率密度函数的不对称程度。偏度的定义为信号幅值的标准三阶中心矩：

信号的峭度描述信号所有取值分布形态陡缓程度的统计量，为无量纲参数，峭度的定义为信号幅值的标准四阶中心矩与方差平方的比值：

式（11）～（12）中P为信号的偏度；K为信号的峭度；μ为信号x的均值；σ为信号的标准差。

微震与爆破信号上述4个分量的偏度和峭度概率密度分布如图3所示。图3（a）中，小于0的区间内，微震信号偏度概率密度值均大于爆破信号，而大于0的区间则相反。该分量的偏度参数具有一定程度的识别效果，但由于集中在－0.5～0.5之间，来自不同类别集的样本特征值差异性有限。图3（b）中，IMF1的偏度概率密度分布均呈正态分布趋势，微震信号偏度值集中在－0.4～0.8之间，爆破信号则集中在－0.8～0.4之间。该分量的偏度值具有较好的识别效果，虽然来自相同类别集的不同样本的偏度值有差异，但不同类别样本间的偏度值服从不同的正态分布。图3（c）和（d）中，相同区间内的概率密度分布差异较小，因此该参数识别效果有限。图3（e）中，微震重构分量峭度值集中在20～40区间内，该参数具有一定的差异和参考价值。从图3（f）可知，爆破信号IMF1峭度值集中在30～60之间，而微震信号则在22.5～120之间均匀分布，不同类别样本的参数差别较大。图3（g）和（h）中，两类信号的IMF2和IMF3峭度值分布相似，参数差异较小，无法有效识别两类信号。

图3 各IMF分量偏度和峭度概率密度分布

Lempel-Ziv复杂度算法（简称LZC）可反映有限时间信号序列随长度增加、内部出现新模式的速率，复杂度越大，新模式出现速率越快。主要计算流程参见文献［15］。

图4为两类信号的LZC概率密度分布。图4（a）中微震信号的LZC值集中分布在0.09～0.18，爆破信号则在0.12～0.27之间均有分布，表明随着长度增加，微震信号内部新模式出现的速率小于爆破信号。图4（b）中，IMF1分量LZC值在0.1～0.8之间均有分布，由于两类信号的LZC值分布区间重叠交叉部分较多，差异性略小于重构分量。图4（c）中，IMF2分量的LZC概率密度值分布逐渐降低，相同区间内两类信号之间没有明显分界，因此该参数识别效果较差。

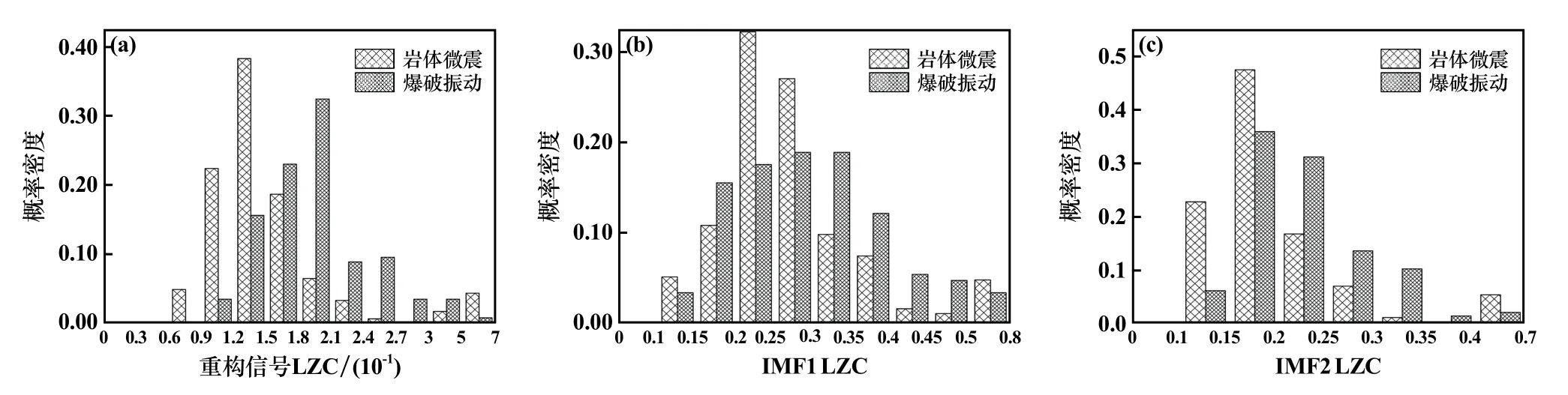
图4 各IMF分量LZC概率密度分布

图5为两类重构信号的分形盒维数概率密度分布。图中两类信号分形盒维数值各自服从不同的正态分布，其分布中心分别是微震信号在1.275～1.35之间、爆破信号在1.38～1.475之间；两者在1.33～1.375之间有一定重叠部分，表明两类信号的分形盒维数特征存在一定的相似性。整体上微震信号的分形盒维数值低于爆破信号，这是由于微震事件产生的信号波形较单一，而爆破信号相对更复杂，该特征也符合LZC值的分布特点。

图5 重构信号分形盒维数概率密度分布

边际谱能量分布比例均值如表1所示。表1中，两类信号的边际谱能量分布具有明显的差异，具体表现为：随着IMF分量阶数增加，边际谱能量比例逐渐减小，微震信号能量主要集中在前三个分量，比例为99.6%，其中IMF2比例最大，为41.18%；爆破信号主要集中在前两个分量，比例为94.13%，其中IMF1比例为73.52%。

表1 边际谱能量分布比例均值

4 基于GA-SVM网络的信号识别

4.1 GA-SVM模式识别模型建立

GA-SVM模型构建流程如下：

1）构建特征向量，提取出识别对象特征参数。本文构建400×28特征向量集，从中随机选取微震和爆破信号各150组数据作为训练样本，其余各50组数据作为预测样本。设定微震信号标识为1，爆破信号标识为2。

2）将训练集和测试集特征向量归一化：

式中xi和xi′分别为归一化前后的特征向量。

计算特征向量中每个参数的LS值，选出信号的敏感信息特征，提高模型的准确率。

3）设定惩罚因子C和核函数γ的取值范围分别为［0，100］和［0，1 000］。初始种群数设为100，最大迭代次数200次，交叉概率pc＝0.6，变异概率pm＝0.06。

4）采用筛选后的特征向量对模型进行训练，经遗传算法GA寻优的参数为：惩罚因子C＝4.52，核函数参数γ＝3.64，选择RBF核函数训练SVM网络。

4.2 基于Laplacian-score的特征降维

表2为28维特征向量的LS值。LS值越大相应特征参数重要性越高。为验证LS算法的效果和所选特征向量的适用性，将不同分形维数的特征向量在GA-SVM模型中的识别率绘制成图，如图6所示。随着特征向量分形维数增加，识别率逐渐增高，表明LS算法具有良好的特征选择性能；当分形维数增加到15左右，识别率趋于稳定，当分形维数增加到20以后，识别率略有降低，但仍维持在较高水平。分析认为分形维数增加造成特征向量中冗余信息提高，降低模型计算精度，故选取前17种特征参数组成复合特征向量。

图6 不同特征分形维数的分类性能

表2 特征参数LS值

4.3 分类识别结果

为验证GA-SVM方法的优越性，另外选取SVM、LR、Bayes算法进行对比，其中LR、Bayes算法的先验概率均为0.5，4种模型均采用17维复合特征向量为识别对象，表3为分类识别结果。结果表明，在同种识别模型下，改进HHT的识别结果整体上优于传统EMD和LMD方法，表明改进HHT可以更充分提取两类信号的特征；同一特征向量下，GA-SVM的分类效果明显优于SVM、LR和Bayes模型，并且与改进HHT结合的准确率达到95%。表明基于改进HHT和GA-SVM算法构建的识别模型准确率高，能够有效识别出岩体微震和爆破振动信号。