城市地下矿山地表感知风险模糊ISM-BN评价模型与应用①

2023-01-12胡建华杨庆芳曾平平徐朔寒

矿冶工程 2022年6期

胡建华，杨庆芳，曾平平，周坦，徐朔寒

（中南大学资源与安全工程学院，湖南长沙 410083）

矿产资源是国民经济可持续发展的重要基础，但地表水体、建筑物和铁路（公路）下矿体（“三下”矿体）的安全开采问题凸显［1-2］。其中，城市地下矿体开采为典型的“三下”矿体开采［3］，在其开采过程中，会引起矿层岩体的应力场重新分布和位移变形［4］，导致出现矿井突水、地面沉陷和建（构）筑物坍塌等灾害，影响矿山生产和城市安全［5-7］。

安全分析和评价是保障矿山生产的技术措施之一。目前国内外学者通过不同的理论和方法对矿山进行安全评价，取得了大量研究成果，但对城市地下矿山地表风险评价研究相对较少。城市型矿山对居民的影响具有独有的特性且城市居民的感知是对风险最直观的表现。现有的城市地下矿山地表风险评价研究大多只考虑了生态环境的影响指标，缺少对地表人群心理及舆情的分析与探讨。本文在已有研究基础上，对城市地下矿山地表感知风险表征因素开展研究，综合模糊数学理论和解释结构模型（ISM）的优势特征，对贝叶斯网络（BN）进行改进，构建基于模糊ISM-BN的城市地下矿山地表风险评价模型，并以某城市地下铜矿为例，进行地表感知风险评价与分析，为城市地下矿山安全管理提供新的理论参考。

1 风险评价模型构建方法

为了使风险评价模型的分析结果更加科学客观，利用模糊数学、解释结构模型（ISM）和贝叶斯网络（BN）等数学方法，构建基于模糊ISM-BN的风险评价模型，对城市地下矿山地表感知风险进行科学评价与分析。构建流程如下：

1）构建城市地下矿山地表感知风险评价指标体系。确定系统要素关系，建立系统要素关系表。2）建立解释结构模型（ISM）。

①建立邻接矩阵［8］：

②通过布尔矩阵运算法则，将邻接矩阵X转换为可达矩阵，其公式［8］分别为：

式中r＝1，2，3，…，n；I是与X同阶次的单位矩阵。

③分解可达矩阵［8］，具体如下：

式中R（Ti）为可达集合；Q（Ti）为先行集合；U（Ti）为最高集合。

④抽取各层级因素，确定系统结构模型。首先，分析可达集合R（Ti）与先行集合Q（Ti）的区域分解结果；其次，利用最高集合U（Ti）对各层级进行因素抽取，确定不同层级因素；最后，结合各层级影响因素和可达矩阵关系，建立系统结构模型。

3）建立贝叶斯网络结构。将系统结构模型中的各层级因素转换为贝叶斯网络节点并将各因素关系转换为贝叶斯网络的有向边。

4）计算贝叶斯网络节点先验概率和初始概率。首先，计算节点先验概率，根据最大熵原则，应用数据统计方式对定量指标进行计算；根据模糊数学综合评判法或专家评分的方式对定性指标进行计算。然后，将先验概率输入到Netica软件进行参数学习，计算得到贝叶斯网络节点间的初始概率。

5）城市地下矿山地表风险分析。首先，分析各节点的初始概率分布信息，由最大隶属度准则确定城市地下矿山地表感知风险等级；然后，通过软件进行正向因果推理预测分析和反向诊断推理分析，确定指标之间的关系与影响程度。

2 城市地下矿山地表风险评价指标体系构建

城市地下矿山地表感知风险评价是一个多层次、多目标的系统工程。充分考虑城市地下矿山在开采运行时对地表产生的各类影响因素，建立城市地下矿山地表感知风险评价的指标体系。从人、机、物、管、环五大系统出发［9-11］，将城市地下矿山对地表感知的安全影响因素（T）分为环境风险因素（A）、安全事故风险因素（B）和社会风险因素（C）三大类，再细分为19个影响因素，即化学性指标（A1）、毒理学指标（A2）、沉降位移（B1）、倾斜（B2）、曲率（B3）、水平变形（B4）、危害程度（B5）、堆积容量（B6）、地震烈度（B7）、尾矿坝状况（B8）、渗流情况（B9）、排洪情况（B10）、监测系统（B11）、日常管理（B12）、应急能力（B13）、安全距离（B14）、作业人员状态（B15）、安全措施（B16）和居民满意度（C1）。具体关系可表示为：

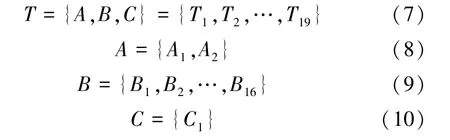
式中T为系统目标因素；T1，T2，T3，…，T19为系统因素。该城市地下矿山地表的具体风险评价指标体系如图1所示，表1为系统因素对应关系。

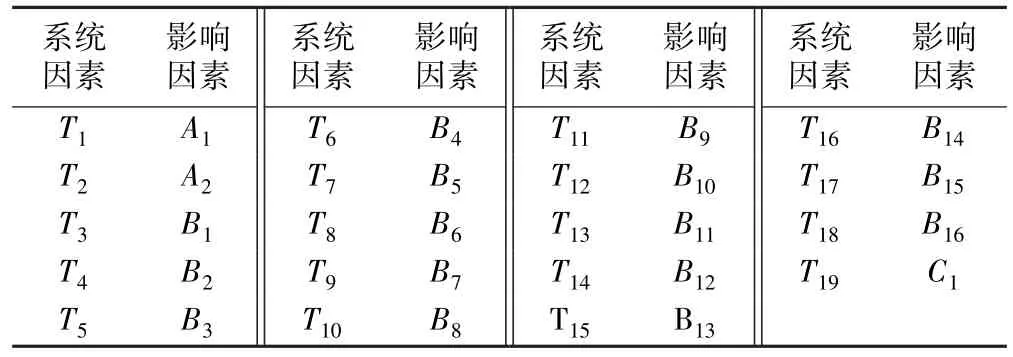
表1 城市地下矿山地表安全系统因素对应关系

图1 城市地下矿山地表风险评价指标体系

3 某铜矿山地表风险评价模型构建

3.1 案例背景

某城市型铜矿每年地下开采21.5万吨，地表分布有水库、医院、学院、政府、矿山主副井、尾矿坝和风景区等建（构）筑物。依据《有色金属采矿设计规范》（GB 50771—2012）规定的地表建（构）筑物的保护等级划分规定，该矿区内地表的医院、学院、政府等属于Ⅱ级保护建（构）筑物，矿山主副井、尾矿坝和风景区等属于Ⅰ级保护建（构）筑物。矿区以北0.5 km的水库可储水1.2亿立方米，是市区的主要供水水源。为合理开采地下矿产资源，实现风险的可预知性，根据城市地下矿山地表风险指标体系，构建基于该铜矿山的模糊ISM-BN风险评价模型。

3.2 建立解释结构模型（ISM）

1）邻接矩阵X。因素分析以专家打分进行评价，邀请了涵盖采矿、选矿、安全、爆破、机械等行业的10位专家，对该19个影响因素进行两两分析，确定影响因素之间的相互关系，再根据式（1）得到邻接矩阵X。

2）可达矩阵及其分解。根据式（3）对邻接矩阵进行布尔运算。经计算，当r＝3时，M＝（X＋I）4＝（X＋I）3≠（X＋I）2≠（X＋I）。得到可达矩阵：

将可达矩阵M＝［mij］19×19进行分解，分别得到可达集合R（Ti）、先行集合Q（Ti）和最高集合U（Ti）。

3）确定系统结构模型。根据式（6），可确定各层级的影响指标集合，分别为L1＝｛T15，T19｝，L2＝｛T2，T12，T16｝，L3＝｛T10，T17，T18｝，L4＝｛T9，T11｝，L5＝｛T1，T3，T4，T5，T6，T7，T8，T14｝，L6＝｛T13｝。遂建立该铜矿山对地表风险影响的系统结构模型如图2所示。

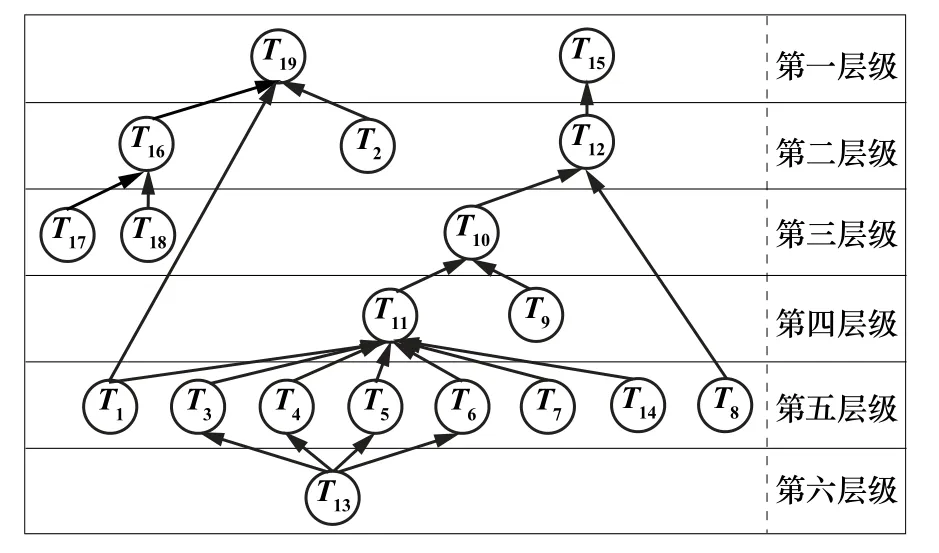
图2 某铜矿山地表风险系统结构模型

3.3 建立贝叶斯网络结构模型（BN）

将该铜矿山对地表风险影响的系统结构模型转换为贝叶斯网络结构，得到该铜矿山对地表感知风险影响的贝叶斯网络结构如图3所示。

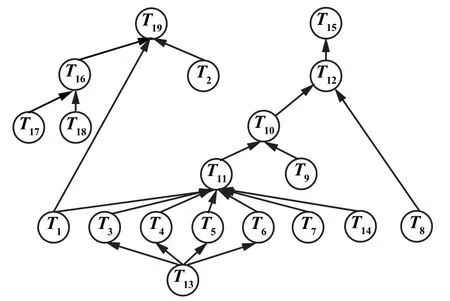
图3 某铜矿山地表风险贝叶斯网络结构

3.4 先验概率及初始概率计算

依据各项指标的行业规范，将风险划分为4个等级（Ⅰ级、Ⅱ级、Ⅲ级和Ⅳ级），详见表2。

表2 城市地下矿山地表风险等级划分

根据该矿山监测数据及行业安全规范，采用定性与定量指标相结合的方式，对各项指标进行确定。最终确定的各节点的先验概率见表3。

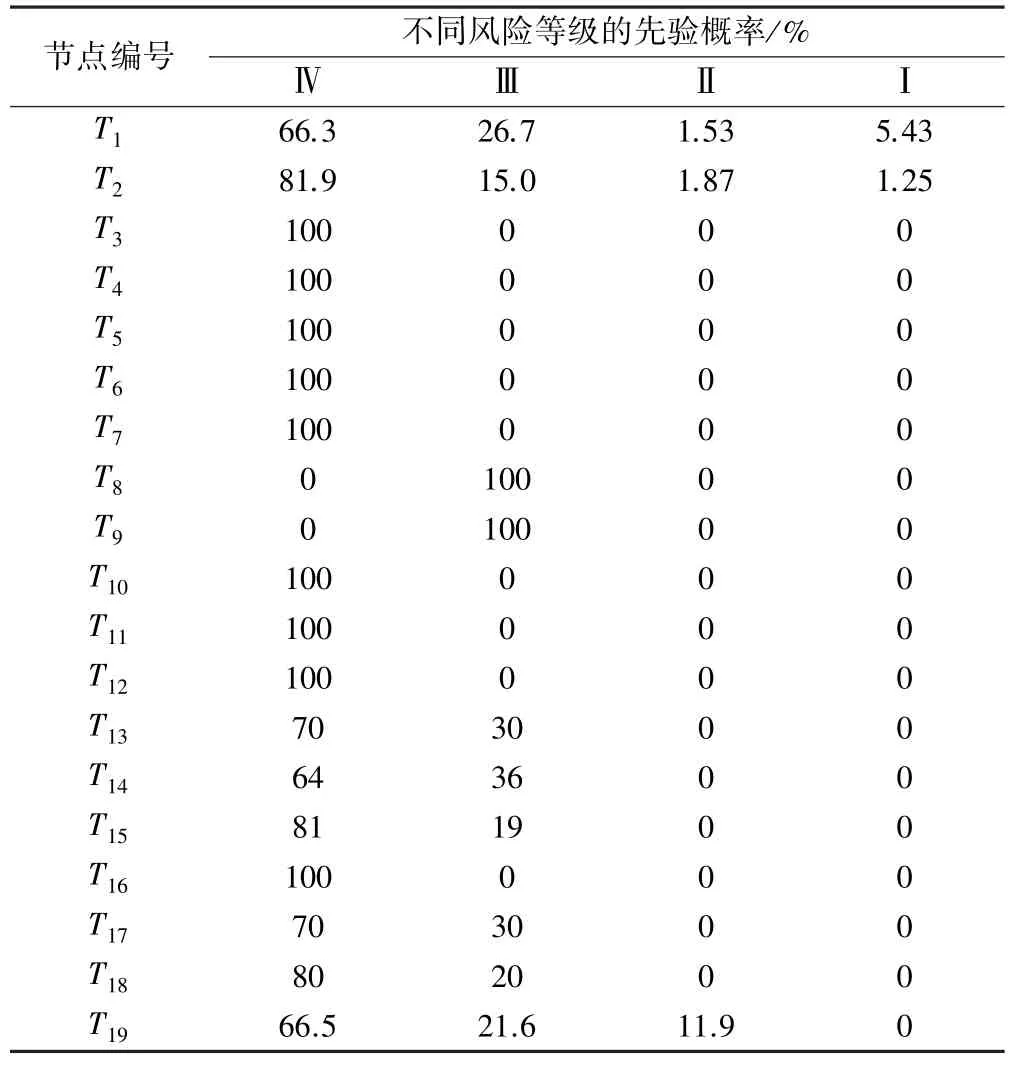
表3 贝叶斯网络节点先验概率

结合ISM构建出的地表感知风险结构模型和各节点的先验概率，软件计算得到各节点的初始概率并确定贝叶斯网络拓扑结构。由初始概率值开展地表风险分析，同时确定的贝叶斯网络拓扑结构也可为正向推理和反向诊断提供支持。

4 某铜矿山地表感知风险分析

4.1 初始概率分布分析

根据各网络节点的初始概率值，进行初始概率分布分析，4个等级的初始概率分布见图4。由图4（a）和图4（b）可见，Ⅰ、Ⅱ级风险下影响指标的初始概率分布相似，大部分影响指标的初始概率偏低（小于10%），而尾矿坝状况（T10）、渗流情况（T11）、排洪能力（T12）、应急能力（T15）、安全距离（T16）和居民满意度（T19）的初始概率虽高于10%，但不超过25%；由图4（c）可见，Ⅲ级风险下，堆积容量（T8）和地震烈度（T9）的初始概率为100%，其他影响指标的初始概率低于50%；由图4（d）可见，大部分影响指标在Ⅳ级风险下的初始概率高于50%。由综合分析可知，各影响指标在Ⅳ级风险下的初始概率远远高于其在Ⅰ、Ⅱ级风险下的初始概率。依据最大隶属度准则，评价确定该铜矿山对地表造成的感知风险等级为Ⅳ级，说明该铜矿对地表的影响较小，未对城市生活造成不便或破坏，其风险程度可接受。

图4 贝叶斯网络初始概率分布

4.2 正向推理预测分析

基于确定的贝叶斯网络拓扑结构，假定目前地下水的化学性指标（T1）处于Ⅰ级风险状态，即设化学性指标（T1）为证据变量，求解其他节点变量的后验概率。在贝叶斯网络拓扑结构中将化学性指标T1的变量状态设置成D＝100%状态，表示证据变量的已知状态，应用Netica软件的自动更新功能更新整个网络节点的后验概率。对比正向推理后验概率与初始概率如图5所示，发现尾矿坝发生高渗流（T11为Ⅰ级风险）的概率由17.6%变成了25.0%，增幅为42.0%；居民产生不满意（T19为I级风险）的概率由15.9%变成了25.0%，增幅为57.2%；而其他影响指标概率无明显变化。可见该矿山地下水的化学性指标（T1）对尾矿库的渗流情况（T11）和居民满意度（T19）有着较大影响。工程实际表明，地下水化学性指标恶化会对排渗设施造成腐蚀和损坏，影响尾矿库正常排渗活动；同时还会影响居民用水，导致居民生活不便，引发社会舆论。可以发现证据节点变量状态变化对节点概率的影响与工程实际一致。

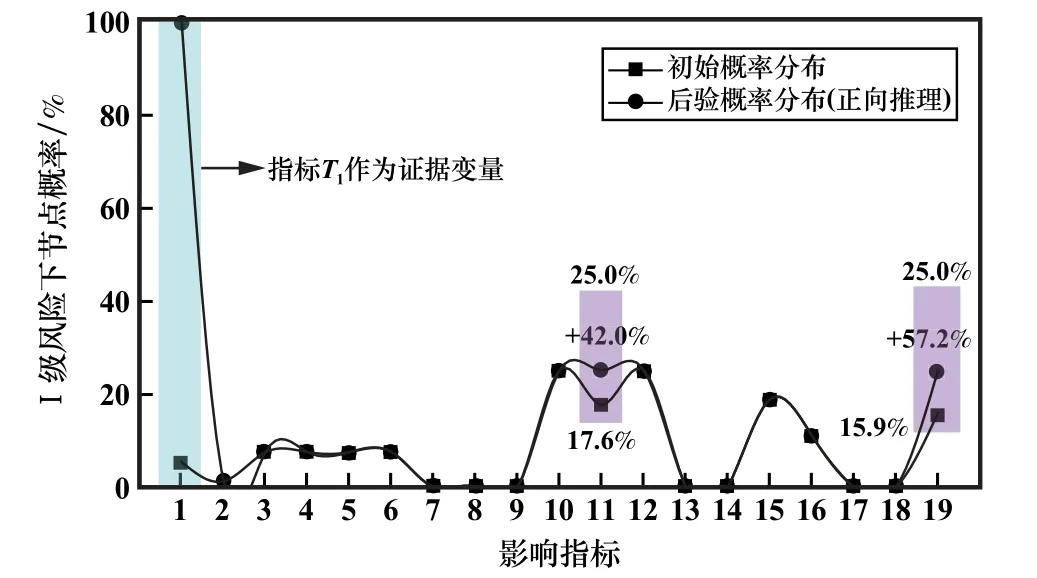
图5 正向推理后验概率与初始概率分布对比

4.3 反向诊断推理分析

以居民满意度（T19）处于Ⅰ级风险为例进行原因诊断，即设证据变量为居民满意度（T19），将其状态的概率设置为D＝100%。输入证据之后启用软件自动更新功能，得到整个网络节点的后验概率。对比反向推理后验概率与初始概率（见图6）的概率变化，此时地下水化学组份含量高（T1为Ⅰ级风险）的概率由5.43%变成了8.54%，增幅为57.3%；地下水含毒组分含量高（T2为Ⅰ级风险）的概率由1.25%变成了1.96%，增幅为56.8%；尾矿坝发生高渗流（T11为Ⅰ级风险）的概率由17.6%变成了19.7%，增幅为11.9%；矿山企业炸药库与周边建筑的安全距离短（T16为Ⅰ级风险）的概率由11.0%变成了17.3%，增幅为57.3%；而其他影响指标的概率无明显变化。计算结果表明，居民产生不满意（T19为Ⅰ级风险）时，在缺乏其他证据的情况下，可能原因是矿山地下水污染程度高（T1、T2为Ⅰ级风险）、尾矿坝发生高渗流（T11为Ⅰ级风险）和矿山企业炸药库与周边建筑的安全距离短（T16为Ⅰ级风险）。且其中地下水化学性指标（T1）和安全距离（T16）对居民满意度（T19）的影响很大，即表示居民满意度（T19）的关键性影响因素为地下水化学性指标（T1）和安全距离（T16）。分析发现，地下水污染程度高，会影响城市居民的日常用水；该矿山的尾矿库处于市区上游，一旦发生事故，会造成巨大的人员伤亡和经济损失，直接影响到居民的生命财产安全；另外，城市居民普遍比较关注企业民用爆炸物品储存库的地理位置。为维持好居民满意度，需加强对这些因素的管理，保障矿山运营安全。