基于博弈论组合赋权的硫化矿山炸药自爆危险性GRA-TOPSIS评价模型①

郭 勇，阳富强

（福州大学 环境与安全工程学院，福建 福州 350116）

截至2019年底，我国已发现的硫铁矿资源存量达62.8亿吨［1］。在开采硫化矿床时，破碎、裸露的硫化矿石会发生放热反应，使得炮孔内热量聚集、温度上升，导致炸药自爆［2-3］。浅层矿产资源日渐枯竭，深度开采已是大势所趋。然而，深度开采会带来地应力增大、地温升高等问题，进一步加剧炸药自爆事故的发生。炸药自爆事故不仅严重影响企业采矿生产系统的正常运行，还会导致人员伤亡。因此，开展硫化矿山炸药自爆危险性评价，对预防、控制和减轻炸药自爆风险具有一定指导意义。

硫化矿山炸药自爆是多种因素相互耦合作用的结果，包括矿样的物理化学因素、矿山环境条件、装药时间等［4］。部分学者研究了炸药自爆的多种因素，运用不同模型对硫化矿山炸药自爆危险性开展了评价，如解释结构模型［5］、未确知测度模型［6］、可变模糊评价模型［7］、云模型［8］、集对分析模型［9］等，但研究多以单一评价模型为主，对各指标之间的关联性以及多维空间的实际距离考虑不足，同时缺乏比较全面的评价指标体系及评价方法。

鉴于此，本文基于硫化矿山炸药自爆的多种影响因素，建立硫化矿山炸药自爆危险性评价体系；采用博弈论综合层次分析法所得主观权重和熵值法所得客观权重，进一步缩小两种方法所得权重和综合权重之间的偏差；将灰色关联分析（Grey Relational Analysis，GRA）和逼近于理想解的排序法（Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS）相结合，既弥补了单独使用TOPSIS对有限数据进行评价时存在的难以找寻数据典型分布规律及变化趋势等缺陷，也能充分考虑到各评价指标之间的联系；最后，通过将该模型应用于典型矿山炸药自爆危险性评价，验证其可行性与优越性。

1 博弈论组合赋权

1.1 层次分析法确定主观权重

层次分析法（Analytic Hierarchy Process，AHP）确定主观权重的基本步骤如下：

1）每位专家根据1～9分制量表对各评价指标打分，得到判断矩阵A＝（bij）n×n。

2）计算判断矩阵的最大特征值λmax。按式（1）及式（2）对λmax进行一致性检验：

式中RI为平均随机一致性指标，RI与n的取值有关。CR＜0.1，表明判断矩阵一致性良好。

3）计算判断矩阵的λmax所对应的特征向量W＝（w1，w2，…，wn），归一化处理后得到各指标权重θ＝（θ1，θ2，…，θn）。

1.2 熵值法确定客观权重

熵值法确定各指标客观权重的步骤如下：

1）按式（3）～（4）计算各评价指标yij的信息熵Ej：

式中qij为归一化处理后的评价指标值；Ej为第j个评价指标的信息熵；当qij＝0时，Ej＝0。

2）按照式（5）计算各评价指标的熵权值（客观权重值）ηj：

1.3 博弈论组合赋权确定综合权重

运用博弈论（Game Theory，GT）思想，通过离差极小化协调不同赋权法所得权重之间的偏差，提高综合权重的精确性［10］。基本步骤如下：

1）构建基础权重向量集uk＝｛uk1，uk2，…，ukn｝（k＝1，2，…，L），则它们的任意线性组合可表示为：

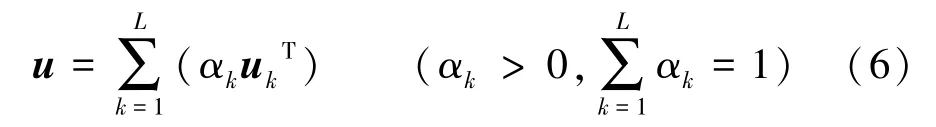
式中u为一种可能综合权重向量；αk为线性组合系数；L为权重赋权法数量。

2）优化权重系数αk，使得综合权重向量u和基础权重向量uk之间的离差最小，即：

3）按照式（8）归一化处理式（7）求得的权重系数（α1，α2，…，αL）：

4）各评价指标综合权重向量为：

2 硫化矿山炸药自爆危险性GRA-TOPSIS评价体系及模型

根据硫化矿山实际情况，通过查阅相关文献［5-9］及分析以往炸药自爆事故案例，将硫化矿山炸药自爆影响因素归为矿样物理化学因素、环境因素、开采工艺条件、管理因素4大类，并进一步将其细化为硫化矿石含水量、采场温度、装药时间等12种正向指标与负向指标。正向指标的指标值越大，炸药自爆危险性越小（矿山安全程度越高）；负向指标的指标值越大，炸药自爆危险性越大（矿山安全程度越低）。具体评价体系如图1所示。本文将C1、C2、C10、C12列为正向指标，将C3、C4、C5、C6、C7、C8、C9、C11列为负向指标。

图1 硫化矿山炸药自爆危险性综合评价指标体系

假设有m个待评价矿山样本，每个矿山包括n个评价指标，构建指标矩阵X＝（xij）m×n（xij为第i个矿山的第j个评价指标）。由于各类指标类型与量纲有所不同，采用极值处理法对指标进行规范化预处理，避免对评价产生影响。规范化处理后的矩阵为Y＝（yij）m×n，具体公式为：

TOPSIS评价的基本思路是计算各样本与评价指标决策矩阵之间正、负理想解的欧式距离，获得相对贴近度，并以此为依据进行排序［11］。GRA评价通过计算各样本与评价指标决策矩阵之间正、负理想解几何形态的相似度，对待评价样本进行排序。两种方法互为补充，GRA法可克服TOPSIS处理有限数据时存在的无法量化系统动态发展状况等问题，TOPSIS可弥补GRA评价时存在的方案整体性考虑不足等缺陷［12］。将两种方法融合后，硫化矿山炸药自爆危险性评价步骤共分为7步。

1）确定加权规范化决策矩阵C＝（cij）m×n。其中，

cij＝yij·u*。

2）选取矩阵C中各指标最优值组成正理想解集，即：

式中ci（j）为各待评价矿山的cij值。

3）计算各待估矿山样本与正理想解集的灰色关联度，得到灰色关联系数矩阵R＝ri（j）m×n：

式中ρ为分辨系数，本文ρ取值0.3。

4）确定正理想解集S＋与负理想解集S－：

6）计算各矿山相对贴近度Ti，并进行排序。相对贴近度的大小反映了待评价矿山的优劣性。Ti越大，待评价矿山越优，即危险性较小；Ti越小，待评价矿山越劣，即危险性较大。

7）确定各矿山炸药自爆危险等级。以相对贴近度为划分依据，形成硫化矿山炸药自爆危险性评价等级区间，见表1。等级Ⅰ、Ⅱ、Ⅲ、Ⅳ分别代表自爆危险性较小、一般、大、极大。

表1 炸药自爆危险性等级量化标准

3 实例运用

选取国内4座典型硫化矿山M1，M2，M3，M4，运用上述GRA-TOPSIS模型对其炸药自爆危险性进行评估。根据历史记录，矿山M1、M2、M3均有过炸药自爆事故，并造成人员伤亡；而矿山M4未发生过相关事故。矿山M1和M3事故严重性超过了矿山M2，矿山M3炸药自爆事故造成的人员伤亡最多，影响最大。各矿山评价指标统计值见表2。

表2 矿山样本评价指标统计值

3.1 计算综合权重

根据矿山样本评价指标统计值建立指标矩阵X＝（xij）4×12，无 量 纲 化 处 理 后 得 到 规 范 化 矩 阵Y＝（yij）4×12。利用式（1）～（2）获取各评价指标主观权重θj，利用式（3）～（5）计算各评价指标客观权重ηj。根据式（6）～（9）将所得权重θj与ηj组合赋权得到综合权重uj*。具体权重值如表3所示。

表3 博弈论所赋各评价指标综合权重

3.2 确定炸药自爆危险性

基于综合权重值，运用GRA-TOPSIS模型对4个矿山样本开展炸药自爆危险性评价。由式（10）～（14）得到加权规范矩阵C见表4，灰色关联矩阵R如表5所示，正理想解集S＋＝［1，1，1，1，1，1，1，1，1，1，1，1］，负理想解集S－＝［0.542 9，0.565 5，0.485 0，0.479 9，0.425 7，0.550 4，0.309 0，0.398 7，0.675 4，0.359 7，0.645 0，0.230 8］。并求得各待评价矿山与S＋、S－的欧氏距离di

表4 加权规范矩阵

表5 灰色关联矩阵

＋、di

－、相对贴近度Ti以及危险性等级如表6所示。

表6 4个矿山样本炸药自爆危险性评价结果

3.3 评价结果分析

为进一步验证该模型的可行性、精确性与优越性，分别利用TOPSIS模型、GRA模型单独对4个矿山样本开展炸药自爆危险性评价，结果如图2所示。将GRA-TOPSIS模型、TOPSIS模型、GRA模型评价结果与以往其他模型的评价结果进行对比，结果如表7所示。

表7 不同模型炸药自爆危险性评价结果

由图2可知，运用不同的模型对4座矿山炸药自爆危险性进行排序时出现了不同的结果。TOPSIS模型：M1＞M3＞M2＞M4；GRA模 型：M4＞M2＞M3＞M1；GRA-TOPSIS模型：M3＞M1＞M2＞M4。根据矿山实际情况，矿山M1、M2、M3均发生过炸药自爆事故，而矿山M4没有相关事故报道；且事故严重性排序为M3＞M1＞M2。由此得知，GRA模型评判结果与矿山实际情况存在较大差异；TOPSIS模型评判结果与矿山实际情况基本吻合，存在些许出入；GRA-TOPSIS模型评判结果与矿山实际情况完全吻合。

图2 不同评价方法相对贴近度

由表7可知，GRA-TOPSIS模型所得4座硫化矿山样本炸药自爆的危险性等级分别为Ⅳ级（极大）、Ⅲ（大）、Ⅳ级（极大）、Ⅰ（较小），与各矿山实际情况相符。未确知度模型和云模型仅利用熵值法来确定权重，未考虑主观权重，使得各评价指标的权重计量存在片面性，导致评价结果准确性与可信度降低。单独运用TOPSIS或GRA模型进行评价时均采用博弈论组合赋权的方法确定各指标的权重，但由于TOPSIS法仅考虑到欧氏距离的计算，GRA法对各矿山整体性考虑较少，导致评价结果不够准确。因此，相比单一赋权方法，博弈论组合赋权容错性更高、协调性更强，可使综合权重更准确；GRA-TOPSIS模型可弥补GRA、TOPSIS模型各自存在的缺陷，使得评价结果更贴近实际情况。

4 结 语

1）选取硫化矿石含水量、采场温度、装药时间、采场管理水平等12种正向和负向指标，建立硫化矿山炸药自爆危险性评价体系。

2）运用博弈论集成层次分析法所得主观权重与熵值法所得客观权重，得到各评价指标综合权重，并构建硫化矿山炸药自爆危险性GRA-TOPSIS模型。

3）将该模型应用于我国4座典型矿山炸药自爆危险性评价中，得到4座矿山炸药自爆危险性排序为M1＝M3＞M2＞M4，危险性等级分别为Ⅳ级（极大）、Ⅳ级（极大）、Ⅲ（大）、Ⅰ（较小），与矿山实际情况相符。对比分析了GRA-TOPSIS模型与TOPSIS、GRA模型以及以往其他模型的预测结果，进一步证明该模型的可行性与优越性。该模型可应用于多个硫化矿山炸药自爆危险性评价，也可在后续研究中尝试将其应用于单个矿区不同采空区危险性评价中，可对多个采空区的危险性进行排序，以便及时采取措施，避免炸药自爆事故的发生。