深入研究一节教材 精心设计导学方案
——以青岛版“二次函数”的概念为例
2023-01-11山东沂南第四中学李树臣山东威海高区一中
⦿山东沂南第四中学 李树臣⦿山东威海高区一中 韩 燕
1 引言
《义务教育数学课程标准(2011年版)》(简称《课标(2011年版)》)提出的提高学生的数学核心素养目标的落实,是通过每一节课堂教学逐步实现的.因此,教师应研读每一节教材,把握每一节教材的编写意图,设计好教学方案,才能保证每一节课的教学质量.
据了解,很多老师的教案没有体现出教材的编写意图,导致教学出现了“偏差”.这部分老师对教材研究的“力度”不够,若长此以往,将很难保证实现《课标(2011年版)》的理念.
本文中以《课标(2011年版)》下青岛版“二次函数”一节课的研究和教学设计为例,旨在说明教师首先应认真研读教材,把握教材编写的意图,才能编写出符合教材要求的导学方案.
2 研读教材的收获
数学教材凝聚了编写者的心血,他们在编写过程中,认真学习、反复推敲《课标(2011年版)》的每一条理论要求,耐心打磨教材中的每一句话(一个字),在比较、斟酌中筛选教材中的每一个例题、练习题.
课堂教学的主要依据是教材.教师在教学前应反复阅读,认真研读,充分理解教材的编写意图.这对于指导教学具有现实意义.
教师只有反复研读每一节(课)教材,才能把握教材的编写意图,明确教材的主要内容,从而确定教学目标,找出教学重点和难点,设计出切实可行的教学方案.
青岛版教材九下“5.3二次函数”主要内容有5个问题、一个例题、两个练习和6个习题.通过研究,可以把其分为三个主要环节.
环节1:二次函数的建立.
整个二次函数的建立过程分三个层次:
第一层次:问题情境导入.
教材在二次函数概念引入前,设计了三个问题:(1)用铁丝围矩形问题;(2)小球沿光滑斜坡滚动问题;(3)企业产值问题.
要求学生分别写出这三个问题中变量之间的函数表达式.
编写意图:初中阶段学生主要学习一次函数(正比例函数)、反比例函数和二次函数,在学习前面两类函数时已经有了下述认知:(1)函数是刻画变量与变量之间依赖关系的模型;(2)函数是联结两类对象的桥梁;(3)函数是“图形”.对函数内容的呈现过程如图1所示.
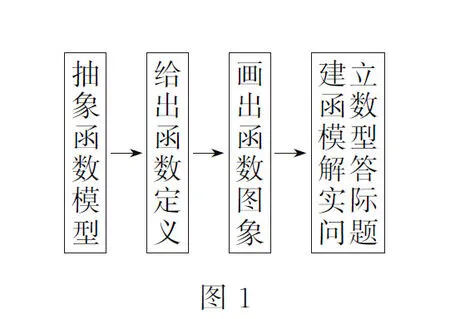
教材在这个基础上,安排了“二次函数”的内容,本节“沿袭”学习前面两类函数的研究过程.《课标(2011年版)》对“二次函数”的第一条要求是“通过对实际问题的分析,体会二次函数的意义”.结合《课标(2011年版)》提出的“现实性”要求,教材从“贴近学生的现实”出发,精心选取了上面的三个问题,其中问题(1)和(3)取材于“生活现实”,问题(2)取材于物理学科.
三个问题立足于学生的“生活现实”,有助于学生从“现实情境”中抽象出数学知识,进一步感悟“数学与生活”的关系,加深对模型思想的认识.这种设计符合“认识到现实生活中蕴涵着大量与数量和图形有关的问题,这些问题可以抽象成数学问题,用数学的方法予以解决”的《课标(2011年版)》要求.
第二层次:抽象本质特征.
教材在这个阶段的文字叙述很简练,仅有三行字,形成了第(4)个问题:
经过整理,以上三个问题中的函数表达式分别是:
①y=x2+30x;②S=2t2;③W=1 200x2+2 400x+1 200.
观察这些函数表达式,你发现它们具有什么共同特征?
设计意图:史宁中教授指出“抽象是从许多事物中舍弃个别的、非本质属性,得到共同的、本质属性的思维过程,是形成概念的必要手段”.抽象能力是数学核心素养的重要组成部分,抽象能力是在学生经历抽象的过程中形成和发展起来的.这个层次的意图就在于培养学生从三个表达式的众多属性中抽象出“共同特征”的能力,从而发展学生的数学核心素养.
第三层次:引入二次函数概念.
一般地,形如y=ax2+bx+c(a,b,c是常数,且a≠0)的函数叫做二次函数.
你能分别说出上述三个二次函数表达式中的二次项系数、一次项系数和常数项吗?
设计意图:数学概念的教学既是数学教学的重要环节,又是数学学习的核心.其根本任务是准确地揭示概念的内涵与外延,使学生在思考问题、进行推理论证时能有据可依,并能创见性地解决问题.数学概念都有非常精确的含义,在第二个层次中,学生对三个二次函数表达式的本质特征有了认识后,教材及时给出了二次函数的定义.这里采用的是“形式定义”法,这种定义虽然能从其中分离出概念的内涵,按规则作外延分类,但又不是从内涵或外延出发而构造相应的模式,它的着眼点在于被定义概念的本质结构.
环节2:二次函数中自变量的取值范围.
教材在这个环节设置了第(5)个问题:
(5)你能说出二次函数y=ax2+bx+c中变量x的取值范围吗?你能分别说出问题(1)(2)(3)中自变量取值的范围吗?
设计意图:在引入二次函数定义后,明确自变量的取值范围对学生理解二次函数以及后面利用二次函数的性质解决实际问题也具有积极的意义.另外,二次函数是用数学式子给出的,在二次函数y=ax2+bx+c的表达式中,每个字母符号都具有自己的意义.单就二次函数的表达式y=ax2+bx+c来说,自变量x的取值范围是没有限制的,x可以取任意实数.但对于从实际问题中抽象出来的具体二次函数表达式y=ax2+bx+c中的自变量必须确保实际问题有意义,这就客观导致了自变量的取值不能“自由任性”,要受到一定的限制,这是学生学习中容易出现问题的地方.基于上面两点,教材给出了问题(5),学生通过思考、讨论问题(5)可以达到上面的目的.
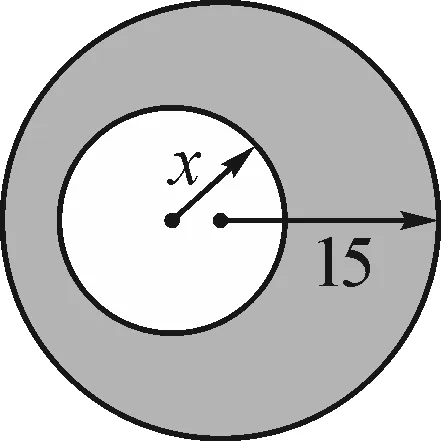
图2
例题如图2,从半径为15的圆形铁片上,挖去一个半径为x的圆.写出剩余部分的面积y与x之间的函数表达式,并指出自变量x可以取值的范围.
设计意图:这是一个实际问题,设计这个题目的目的是让学生进一步明确二次函数与数学的关系,学会建立二次函数表达式,体会建立函数模型的过程,并且加深对自变量取值是有限制条件的认识.
3 二次函数的教学方案
有了上面对教材的研究,可以将“二次函数”这一课的宏观教学方案设计如下:
(一)学习目标.
(1)结合具体情境,通过用表达式表示简单实际问题中变量之间的函数关系,体会二次函数的意义.
(2)经历二次函数概念的形成过程,体会二次函数也是一种数学模型.
(3)会把一个二次函数化成一般形式.
(二)重点难点.
重点:理解二次函数的有关概念,能应用二次函数的相关知识解决简单的问题.
难点:将简单的实际问题转化为二次函数的模型.
(三)教学过程要点.
(1)回顾函数的概念,到目前我们学了哪些函数?你能说出它们的概念吗?
(2)自主探究.
思考下列问题,并与同学们交流.
①把一根长为60 cm的铁丝,围成一个矩形.写出矩形的面积S(单位:cm2)与它的一边长x(单位:cm)之间的函数表达式.
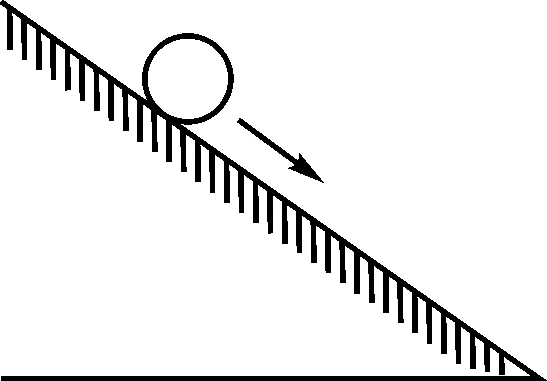
图3
②一个小球由静止开始,沿图3所示的光滑斜坡向下滚动,经过5 s到达斜坡的底部.实验测得小球滚动的距离s(单位:m)与时间t(单位:s)对应的数据如表1所示:

表1 小球滚动的距离与时间对应表
分析表1中的数据,并根据数据回答下面问题:
(ⅰ)当t增加时,s怎样变化?
(ⅱ)s与t之间的函数表达式可能为.
③某企业去年的产值为1 200万元.如果三年内该企业年产值平均每年的增长率为x,你能写出明年该企业年产值y(单位:万元)与x之间的函数表达式吗?
(3)抽象归纳.
观察下面三个函数表达式,它们有什么共同特征?
①y=x2+30x;②S=2t2;③W=1 200x2+2 400x+1 200.
(4)给出二次函数概念.
(5)例题讲解.
讲解例题时,可引导学生列出函数表达式,再由x表示小圆半径,从而得到x>0.另一方面,由于小圆圆心可以与大圆的圆心重合,此时要使小圆在大圆内,x应满足x<15.
(6)尝试应用.
①分别说出下列二次函数的二次项系数、一次项系数、常数项.
(ⅰ)y=-x2+58x-112;(ⅱ)y=πx2.
②当系数a,b,c满足什么条件时,函数y=ax2+bx+c是二次函数?一次函数?正比例函数?
③已知正方形的边长是3,当边长增加x时,面积增加y,写出y与x之间的函数表达式.
4 两点启示
从前面的叙述看,只要在教材研读方面下了功夫,把握了教材的编写意图,编写教学方案就显得很轻松,更重要的是这样编写出的教学方案才是有实效的.通过对青岛版“二次函数”一课的教学研究,我们至少有以下两点体会.
(1)加大研读教材的力度.
首先,教师要树立正确的“教材观”.数学教学必须以教材为蓝本,以教材为根本.要正确理解目前流行的“不是教教材,而是用教材教”“要创造性地使用教材”等“时髦”观点.教学中教师一定要重视教材,研读教材,不能脱离教材.有些老师企图用所谓的“导学案”代替教材是很荒唐的做法.
其次,通过研读教材正确把握教材的编写意图,这是教师编写教学方案的基础,只有这样才能确保编写的教学方案是针对教材的,确保教学真实有效,提高教学质量.
(2)概念教学应贯穿于课堂教学的始终.
数学概念是人脑对现实对象的数量关系和空间形式的本质特征的一种反映形式.数学概念是重要的数学基础知识,是构成数学教材的基本结构单位,正是因为这些数学概念的存在,才形成了数学教材的知识结构.
曹才翰老先生说过,“概念是思维的细胞,数学根本上是玩概念的,不是玩技巧,技巧不足道也”.数学教学必须做到“概念明确”,因为在教学中只有明确概念,才能把握概念的本质属性.数学公式、定理和方法都是反映数学对象和概念间关系的,学生只有建立起了正确明晰的概念,才能牢固地掌握基础知识,进行命题推理.
数学概念贯穿于数学教学的始终,新授课离不开数学概念,复习课更是离不开概念,而一个个的数学知识点就是靠概念“串连”在一起的.通过复习欲达到系统掌握知识的目的,只要把本单元所涉及的概念串连起来就能“再现”教材的知识结构.所以,从数学教学的形式和内容上看,数学概念教学始终与课堂教学并存.
概念教学是培养学生思维能力的起始阶段和基本出发点,学生在深入理解数学概念的过程中能使自己的抽象思维得到发展.可见,数学概念教学的质量,直接影响到学生思维能力的形成,关系到其思维能力的发展.所以,我们要把数学概念的教学融入到教学的全程之中.
