改进蜉蝣算法及其在脑电信号识别中的应用
2023-01-11赵梦玲杨心露殷新宇
赵梦玲,杨心露,殷新宇
(西安科技大学 理学院,陕西 西安 710054)
0 引言
脑-计算机接口(brain computer interface,BCI)是人类大脑和计算机交互的媒介。BCI的最初研究以提高人类独立性和生活质量为目的。文献[1]指出BCI在癫痫发作检测/预测、药物效应诊断、运动图像监测、心理任务、睡眠状态识别等多个领域应用广泛。BCI具有多种范式,事件相关电位(event related potentials,ERP)是其中的一种,主要是大脑在经历感觉刺激时产生的反应。文献[2]提出P300已被证明是ERP成分中有效的活动位点。文献[3]概述了P300技术的现状,并通过对比实验证明了在脑电信号(electroencephalogram,EEG)分类中支持向量机(support vector machine,SVM)的良好性能。文献[4]提出了基于猫群算法(cat swarm algorithm,CSO)优化SVM模型,搜索优化特征子集,保留有益的特征作为SVM分类器的输入。文献[5]总结了多种机器学习方法在BCI分类上的应用,提出了极限学习机(extreme learning machines,ELM)和SVM方法在脑电信号识别领域的优势。
蜉蝣算法(mayfly algorithm,MA)是2020年提出的一种新型智能算法,是一种以蜉蝣生物的飞行和社会行为为参照的元启发式算法,结合了遗传算法和粒子群算法的优势。文献[6]指出了MA中特殊的舞蹈和随机飞行的过程可以增强算法探索能力,利用特性之间的平衡,帮助算法摆脱局部最优,而突变部分可以加强算法搜索新区域的能力。但是与其他启发式算法相同,MA也存在如何提高收敛性的问题。与禁忌搜索和遗传算法等其他元启发式算法相比较,模拟退火算法(simulated annealing algorithm,SA)作为一种启发式寻优算法,具有优于其他算法的局部搜索能力。文献[7]提出了一种基于模拟退火的自适应粒子群优化,通过对权重的改进,提高算法收敛性。文献[8]提出使用Tent混沌序列初始化种群的蜉蝣算法,提高了搜索精度和稳定性。但是从文献统计来看,针对MA性能和实际应用上的研究较少。文献[9]证明了启发式算法可以提高机器学习算法的能力。
本文针对蜉蝣算法收敛性能欠佳和易陷入局部搜索的不足,提出一种基于混沌自初始化和模拟退火优化下的蜉蝣算法(chaos simulated annealing mayfly algorithm,SA-AMA)。对7个基准测试函数的仿真结果表明:与自适应模拟退火优化粒子群算法(simulated annealing adaptive particle swarm algorithm,BSAPSO)和标准自适应权重蜉蝣算法(adaptive mayfly algorithm,AMA)相比,改进后的算法寻优能力和收敛性能具有显著优势。为了证明提出的算法在实际应用上的能力,本文建立SVM分类器,并使用改进后的算法优化其参数,对5位受试者的P300脑电信号进行分类识别。实验结果表明:与K-最近邻(K-nearest neighbor,KNN)、ELM网络和SVM分类器对比,使用改进后算法优化下的SVM分类器识别能力突出。
1 算法改进
1.1 混沌初始化种群
文献[10]指出了混沌映射是一种确定性系统产生的随机性序列,其特点在于相差微弱的初始值可能会带来不同的结果,可以提高优化算法的种群多样化。本文通过比较Logistic、Gaussi、Chebyshev、Tent等多个不同的混沌映射系统,选择Logistic混沌映射生成初始化种群。在蜉蝣算法整体搜索过程中,惯性权重需要遵循逐渐递减的趋势。线性自适应惯性权重相比固定权重在一定程度上提升了算法的搜索能力。使用线性自适应惯性权重w:
(1)
其中:iter为当前迭代数;maxiter为最大迭代数;ωmax、ωmin分别为最大、最小惯性权重,范围设置为[0.2,1.2]。
1.2 优化算法步骤
文献[11]提出了SA的优势在于既能增加种群的多样性,又能跳出局部最优,可以有效与其他算法融合,进一步提高搜索能力。本文使用SA机制改进蜉蝣算法个体的速度更新方式,提高搜索速率和种群多样性。
改进的蜉蝣算法具体实现步骤如下:
步骤1 Logistic混沌初始化各参数:
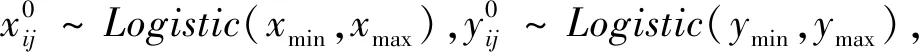

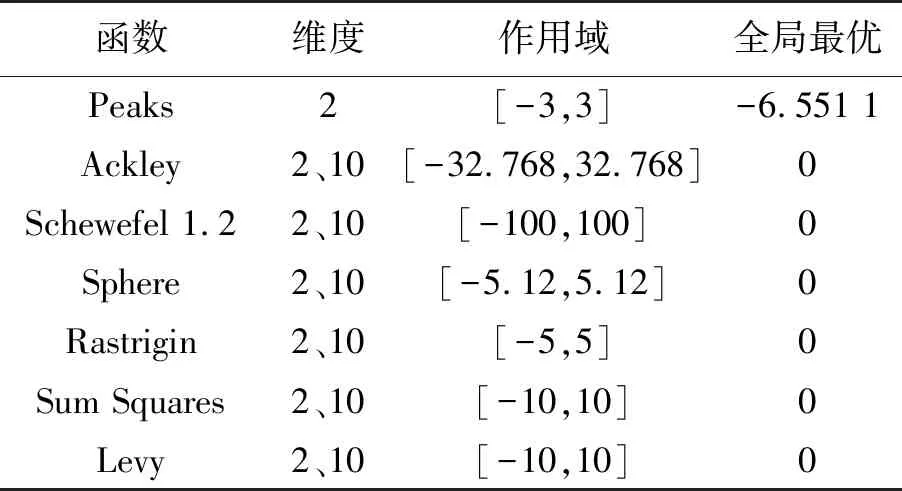
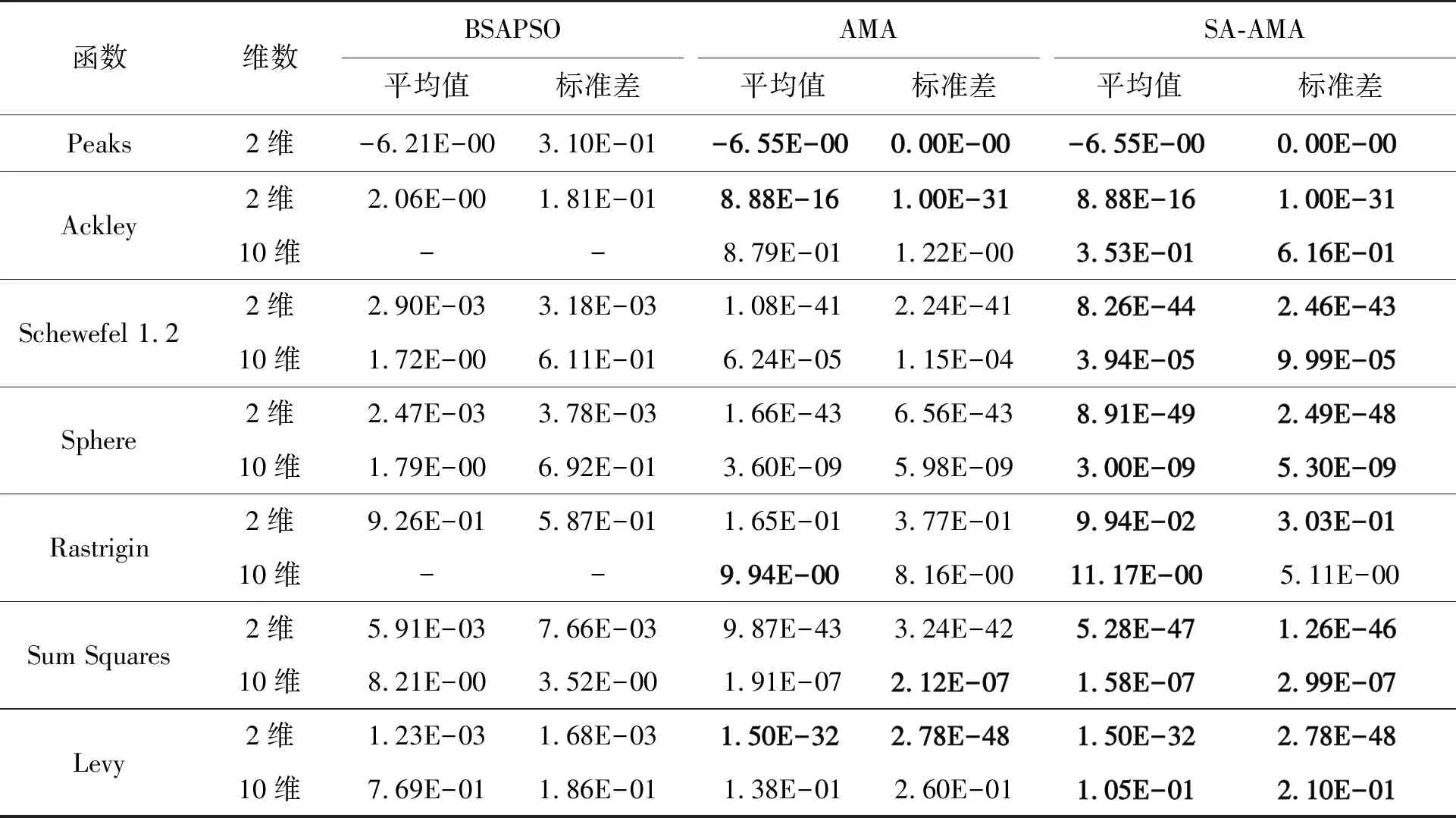
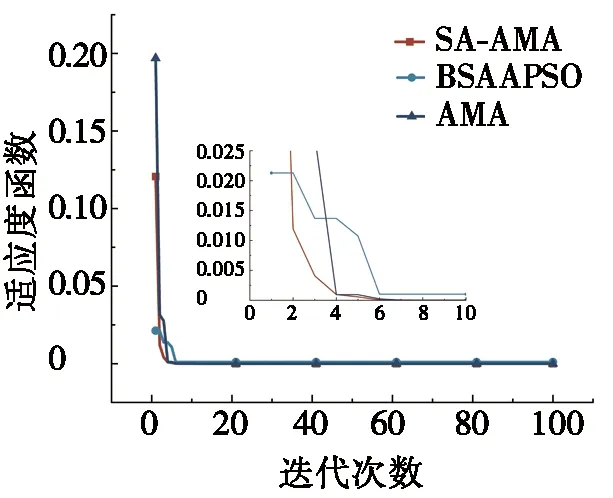
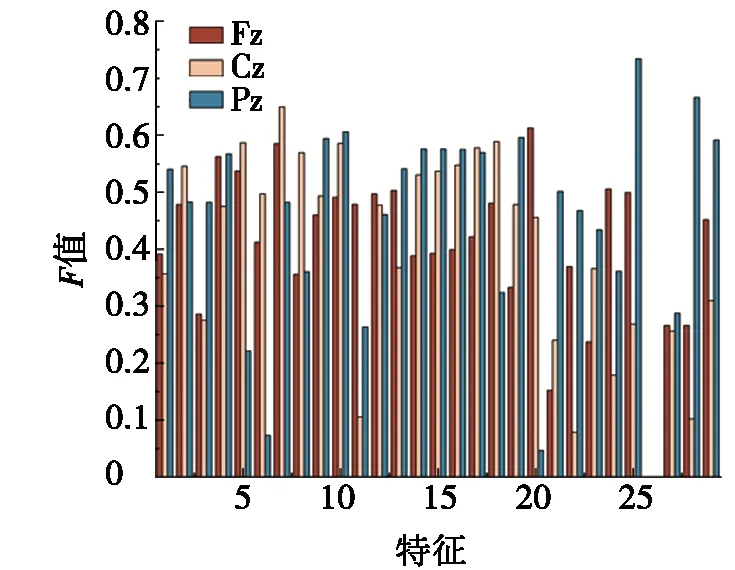
步骤3 迭代前期:iter (2) 式(2)表示雌蜉蝣被雄蜉蝣吸引和未被吸引下雄蜉蝣的速度更新。 雄蜉蝣位置更新公式为: (3) 雌蜉蝣速度更新公式为: (4) 式(4)分别表示雌蜉蝣未被雄蜉蝣吸引和被吸引下雌蜉蝣的速度更新。 雌蜉蝣位置更新公式为: (5) (6) 这里吸引程度通过适应度函数判定,f(yij)>f(xij)表示雌蜉蝣被雄蜉蝣个体吸引,反之,则未被吸引。假设最好的雌蜉蝣个体被最好的雄蜉蝣个体吸引,第二好雌蜉蝣个体被第二好雄蜉蝣个体吸引,以此类推。 步骤4 迭代后期:iter≥max(iter/2),定义概率 (7) 其中:fnew为当前退火阶段的种群个体适应度;以概率p对速度进行调整;t为退火温度,这里设置为100。如果f(yi)>f(xi),以式(2)和式(4)进行速度更新;如果f(yi)≤f(xi),以概率P>rand(0,1)接受个体间吸引更新速度方式,否则,更新进度: (8) 融合模拟退火机制既可以保留算法中的有效更新方式,又提高算法的搜索速度和种群多样性。 步骤5 个体排序后进行交叉和变异产生子代: (9) 步骤6 分离雌性和雄性蜉蝣,更新个体最优各全局最优。返回步骤2,直到满足终止条件。 本文基于MATLAB2020b软件平台进行仿真模拟实验,分析了SA-AMA的计算和收敛性能。所有实验算法的初始种群数量设置为100,最大迭代数设置为100,能见度系数为2,舞蹈系数为5,游走系数为1,a1为1,a2与a3为1.5,突变率为0.01。 为了验证SA-AMA的有效性,本文基于7个测试函数,对SA-AMA、AMA和BSAPSO这3种算法在2维和10维上进行仿真对比,测试函数详见表1。实验独立运行30次,分别计算平均值、标准差,仿真结果见表2。表2中加粗数值表示算法在对应测试函数上的最佳值,缺失数值表示此算法的仿真结果较差,没有对比性。由表2可知:SA-AMA在低维和高维问题上具有优于其他两种算法的搜索能力和收敛能力,可以快速收敛并得到最优解。改进后的算法在测试函数的平均值均达到最佳,标准差也反映了改进后的算法具有良好的鲁棒性。MA拥有不同于粒子群算法的种群变异和交叉能力,因此标准AMA算法的能力较BSAPSO算法有优势,本文所提算法的混沌与模拟退火机制使得算法的寻优速率进一步得到提升。图1是部分测试函数收敛对比图。由图1可得:改进后的算法相比其他两种算法可以快速收敛。由图1a、图1b和图1c可知,基于快速收敛的优势,改进后的算法具有更高的寻优能力。 表1 测试函数 表2 仿真结果 (a) Sphere(2维) 本文采用的P300数据集为5位平均年龄20岁的健康成年人(编号分别为S1、S2、S3、S4、S5),数据采集频率为250 Hz。采用文献[12]的实验设计:每位受试者能观察1个6行6列共36个字符组成的矩阵,并在实验开始前确定1个目标字符。受试者需要注视目标字符,之后进入字符矩阵的闪烁模式,每次以随机的顺序闪烁字符矩阵的1行或1列,闪烁时长为80 ms,间隔为80 ms。当所有行和列均闪烁1次后,结束1轮实验,每次实验产生12个样本。P300电位数据通常在刺激发生后300~450 ms产生正向波峰。每位实验者的单个字符实验P300刺激样本为2个,非P300刺激样本为10个,在受试者注视目标字符的过程中,目标字符所在行或列闪烁,脑电信号中会出现P300电位。而当其他行和列闪烁时,则不会出现P300电位。上述实验流程为1轮,每位实验者共重复5轮。截取每段信号200~500 ms的实验数据,共76个采样点。对负样本的5轮实验所获数据取平均值。通过对12个字符5轮实验数据整理可得,每位受试者完成实验后各有P300和非P300样本矩阵:76×20×120(采样点×通道×样本量)。 实验数据采集基于20个通道:Fz、F3、F4、Cz、C3、C4、T7、T8、CP3、CP4、CP5、CP6、Pz、P3、P4、P7、P8、Oz、O1、O2。可以发现在Fz、Cz、Pz通道上脑电反应最为活跃,并且在刺激发生后300 ms左右出现正向波。文献[13]指出脑电信号的部分通道刺激反映明显。鉴于先验知识,本文选取每位受试者的Fz、Cz、Pz通道数据进行研究。文献[14]指出在脑电信号数据中存在大量干扰,如眨眼、眼动、肌电伪迹、心电伪迹等。经过滤波处理后的信号会过滤掉大多数的噪声,明显提高分类器的分类精度。根据P300的自身特征,其主要信息储存在0~30 Hz的频带中。 独立分量分析(independent component analysis , ICA)是一个线性变换,在独立假设的条件下,可以把数据或信号分离成独立的非高斯信号源的线性组合。ICA通过盲源分离提取有效信息,被广泛应用于语音识别、图像处理、生物医学信号处理、通信、特征提取和降维等领域。ICA将原始信号降维之后,提取相互独立的属性,能够最大程度上挖掘信号的隐藏因素。文献[15]概述了ICA方法的理论过程,与主成分分析(principal components analysis,PCA)方法相比,ICA可以将信号处理为多个统计独立分量的线性组合,应用性更强、更广泛。本文建立低通和高通滤波器,保留0.1~30 Hz的原信号,使用ICA方法在经过滤波处理后的原始信号中分离出有效实验数据。 3.2.1 特征提取 文献[16]指出信号数据具有时域和频域上的多重特性,想要充分研究信号信息,就需要挖掘其最底层的规律。人类大脑的有用信息主要来源于脑电波频带:delta波段(0~4 Hz)、theta波段(3.5~7.5 Hz)、alpha波段(7.5~13 Hz)、beta波段(13~26 Hz)、gamma波段(26~70 Hz)。根据先验经验,P300频域能量主要存在于0~30 Hz频带中,采用功率谱分析/功率谱密度(power spectral density, PSD)方法提取[0.1,3]、[3,5]、[5,7]、[7,13]、[13,30]这5个波段的PSD。同时提取频域特征,即香农熵(Shannon)、对数能量熵(Logenery)、近似熵(ApEn)、幅度最大值、幅度平均值。使用6层4阶紧支集正交(db4)小波包分解原始信号,计算重构信号与原始信号的绝对误差以及小波包分解后在0~30 Hz频段的能量熵值之和。在此基础上,本文还提取了最大值、最小值、中位数、平均值、绝对平均值、方差值、标准差、峭度、偏度、均方根、波形因子、峰值因子、脉冲因子、裕度因子、最大自相关系数、峰值时间、正面积等17个时域特征并进行研究。由此,共提取29个时频域特征。为了便于后续研究,对29个时频域特征进行标序,如表3所示。 表3 29个时频域特征 3.2.2 特征评价 文献[17]提出一种F值(F-score)方法,该方法可以衡量特征在两类之间分辨能力,能够实现最有效的特征选择。每个特征的F值由式(10)计算得到: (10) 使用其对29个特征进行评分和降序重排。图2给出了受试者S5的特征评分值,特征的F值越高,表明其分类能力越强。 图2 S5受试者F-score特征评分 SVM最大的优点是其不受局部最小值的影响,克服了过度学习和高维数据,但这两者都导致了计算复杂度和局部极值。SVM的性能高度依赖于各个参数的合理设定,文献[18]证明了选择合理的参数能有效提高分类模型的学习和泛化能力。 SVM最主要的思想是找到提供最小训练错误数的超平面,并保持约束违反尽可能小,使得两类数据之间的边缘距离最大化,尤其对于线性不可分问题,将输入向量xi通过高维映射(非线性映射)φ(xi)=xi→Η,SVM通过映射将低维线性不可分问题转化为高维可分问题,高维空间H一般为Hilbert空间。 样本xi线性不可分,i=0,1,…,n取整个样本集,间隔最大化(maximal-margin)原则实现最优分类,超平面为: ωT·xi+b=0, (11) (12) 落在上述边界上的样本点(xi,yi)为支持向量,满足: ωTxi±b0=±1。 (13) 软间隔约束凸二次规划问题为: (14) 其中:yi∈{-1,+1},为样本的类别标记;实常数c>0,称为惩罚参数,决定了最小化训练误差和最大化分类边际之间的权衡;ξi≥0,为非负松弛变量,松弛变量可以通过允许违反约束来引入。 本文使用hinge替代损失函数: lhinge(z)=max(0,1-z)。 (15) 引入拉格朗日(Lagrange)乘子αi,只有少部分的样本xi满足yi(wxi+b)=1-ξi,这少部分样本称为支持向量,其对应的Lagrange乘子αi>0,其余样本满足αi=0,体现了稀疏性。优化问题的对偶问题为: (16) 最优决策函数(最优分类器)为: f(x)=sgn(ω*·φ(x)+b*), (17) 其中:ω*、b*均由支持向量决定。 本文使用最小分类误差作为适应度函数,基于径向基核函数(rodial basis function,RBF)作为核函数,使用改进后的算法对最小分类误差进行寻优,得到SVM的最佳参数值并进行分类,使得分类器的性能得到了提升。 文献[19]指出了RBF核函数: (18) 实验的特征是基于最大精度值、最小特征数原则进行选取,这样可以在降低计算成本的基础上获得最优的分类结果。原始数据在经过预处理和特征提取后,使用F值统计量对提取的特征进行评分和重新排序。在进行最终的特征选择和分类前,实验数据在二维平面上呈现出高混合性,若仅在二维空间进行线性分类,其分类难度大且结果欠佳。SVM的最大优势就是使用恰当的核函数将二维数据映射为高维数据,建立最优的空间分类面提高分类能力,从而达到预期的效果。 实验将预处理后的数据按照3∶1分为训练数据和测试数据,使用测试数据的结果作为最终的结论。每位受试者在Fz、Cz、Pz这3个单通道下分别进行特征选择和分类。根据测试集的分类精度,选择出效果最优的特征组合。实验结果表明:表3中的29个时频域特征在最大精度值、最小特征数原则下,0.1~3 Hz的功率谱密度、正面积、裕度因子、香农熵、对数能量熵、中位数、绝对平均值、均方根对受试者分类效果的影响较为明显,说明上述特征在识别中效能显著。 文献[20]指出在分类任务中KNN、ELM和SVM在不同的工程应用问题上具有良好的分类性能。为了比较优化后的分类器性能,本文对比KNN、ELM、SVM、SA-AMA-SVM这4种分类器在P300数据集上的识别能力。KNN采用1~10迭代选取最佳K值,SVM采用10折交叉验证,不同分类器识别率见表4。由表4可知:KNN、ELM、SVM分类器识别能力在受试者S1~S5上各有优势,但是SVM分类器的平均识别能力较高。使用改进后算法优化下的SVM分类的整体识别能力得到明显提升,除在受试者S1上表现欠佳,在其余受试者实验对比达到了最佳的识别率,单通道平均识别率达88%以上,进一步验证了本文所提方法在脑电信号识别应用中的有效性。 表4 不同分类器识别率 % 在现有蜉蝣算法的基础上,本文提出了SA-AMA,改进后的算法提升收敛速率和寻优能力。与AMA和BSAPSO相比,SA-AMA具有更强的鲁棒性和更好的搜索能力。为了测试其实际应用能力,基于时频域特征,使用改进算法优化SVM分类器。SA-AMA-SVM分类器比KNN分类器和ELM分类器识别率更高。因此,本文提出的方法为脑电信号识别提供了新的解决方案和思路。 由于改进算法仍具有一定复杂度,优化的运行时间较长,且虽然脑电信号的识别精度较高,但仍远未达到零误差。未来的研究将侧重于降低算法的复杂性和提高其准确性。
2 仿真模拟
3 应用
3.1 数据处理
3.2 特征提取与选择

3.3 分类器

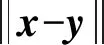
3.4 实验

4 结束语
