基于深层卷积神经网络的震级快速估算方法
2023-01-10王自法廖吉安王延伟位栋梁赵登科
王自法, 廖吉安, 王延伟, 位栋梁, 赵登科
1 中国地震局工程力学研究所, 哈尔滨 150080 2 中震科建(广东)防灾减灾研究院有限公司, 广东韶关 512026 3 河南大学土木建筑学院, 河南开封 475004 4 桂林理工大学广西岩土力学与工程重点实验室, 桂林 541004
0 引言
目前,地震预报仍然是难以解决的世界性难题,而在地震发生后,越快速确定地震信息就越有利于减轻地震灾害.地震预警系统是在地震发生后,在破坏性地震波到达目标区域前,利用初始几秒的地震波确定地震信息(地震位置、震级、预测地震动等),并向目标区域发出警报信息,使得目标区域能够有几秒至几十秒的反应时间.尽管应急反应时间是秒级的,但这对震时的避险逃生极为重要,尤其是对于很多重大工程的紧急处置也非常重要,例如高速铁路、核电站、燃气公司等(Allen and Melgar, 2019)的紧急处置.震级作为地震预警系统的关键参数,其准确性直接关系到地震预警的成败,如何在尽量短的时间内准确地确定震级是地震预警的关键科学问题之一,也是地球物理领域和地震工程领域研究的热点课题.

深度学习是近几年兴起的一种可以从数据中自动学习特征的机器学习方法,在诸多领域取得了巨大的成功(Lecun et al., 2015),如图像识别、语音识别、机器翻译等.受这些领域的研究启发,深度学习方法开始被用于解决地震领域的问题,包括余震预测(DeVries et al., 2018)、震相捡拾(Perol et al., 2018; Ross et al., 2018; Wang et al., 2021; 张逸伦等, 2021)、事件判别(Li et al.,2018)、接受函数的挑选(甘露等, 2021)、高分辨率地震目录生成(苏金波等, 2021)等,并且同样取得了显著的成果.也有学者利用深度学习估算震级,Lomax等将50 s三分向地震波作为CNN(Deep Convolutional Neural Networks)方法的输入,估算4~9级地震的震级(Lomax et al.,2019).Mousavi和Beroza(2020)将完整的三分向地震波作为卷积-循环神经网络的输入,实现了-0.3~5.7级地震的震级估算.Van Den Ende和Ampuero(2020)利用完整的三分向地震波作为CNN方法的输入,实现了3~6级地震的震级估算.Zhang等(2021)将初至4 s以上的三分向地震波作为CNN方法的输入,实现了6级以下地震的震级估算.从前述研究可以看出,深度学习方法可以从地震波中自动提取特征实现震级估算,避免了人为干预,但这些研究所提方法的不足在于,需要输入较长的地震波或者仅能估算较小地震的震级(6级以下),因此,这些方法不适用于地震预警系统的震级估算.
本文提出了一种CNN方法,该方法以端到端的形式,实现了利用单台站的初至3~10 s竖向地震波估算震级.利用日本和智利的约17万条强震记录(震级4~9)对CNN方法进行训练、验证和测试,利用美国和新西兰的地震记录对CNN方法进行泛化能力测试,并与Pd方法进行对比,结果表明所提CNN方法的震级估算效果显著优于Pd方法,可以为地震预警提供更好的震级估算.
1 数据来源
本文以日本KiK-Net(Kiban Kyoshin Network)和K-Net(Kyoshin Network)以及智利SIBER-RISK(Simulation Based Earthquake Risk and Resilience of Interdependent Systems and Networks)的地面强震动记录作为算法研究数据集.数据筛选条件和处理方法:(1)为保证地震记录至少具有初至3 s的P波,以及尽量包括近海的大地震事件,震源距取25~200 km,震级(MW)取4~9级;(2)记录所属监测台站的场地数据中有Vs30(地下30 m深度的平均剪切波速);(3)每条地震记录的三分向合成峰值加速度大于等于2 Gal(Cheng et al., 2014),且信噪比大于20 dB(Nazeri et al., 2017);(4)对于200 Hz采样频率的记录降采样为100 Hz;(5)利用STA/LTA(short-time-average through long-time-average trigger)方法(Allen, 1978, 1982)自动捡拾每条记录的P波到时,并人工进行检查和修正P波到时;(6)对于存在基线漂移的记录,用去均值的方法(减去震前部分的平均值)修正基线;(7)加速度记录经过两次积分得到位移记录,为避免积分造成基线漂移,在每次积分之后对记录进行0.075 Hz的高通滤波(Wu and Zhao, 2006).最终,用于算法研究的数据集共有170324条竖向强震动记录,其中,日本164735条记录(3755次地震事件),智利5589条记录(1275次地震事件).在此数据集中,以记录产生时间的先后顺序组成训练数据集、验证数据集和测试数据集(图1所示):98257条记录作为训练数据集(包括日本1997—2011年的95503条记录和智利1985—2015年的2754条记录),约占总数据集的58%,用于训练CNN方法;31429条记录作为验证数据集(包括日本2012—2014年的29476条记录和智利2016—2017年的1953条记录),约占总数据集的18%,用于优化CNN方法的模型参数;40638条记录作为测试数据集(包括日本2015—2019年的39756条记录和智利2018—2021年的882条记录),约占总数据集的24%,用于检验和对比CNN方法估算震级的效果,此外,为了探究CNN方法对于8和9级特大地震震级估算的能力,将2003年8级地震记录和2011年9级地震记录划分至测试数据集,用以测试CNN方法预测特大地震震级的能力.
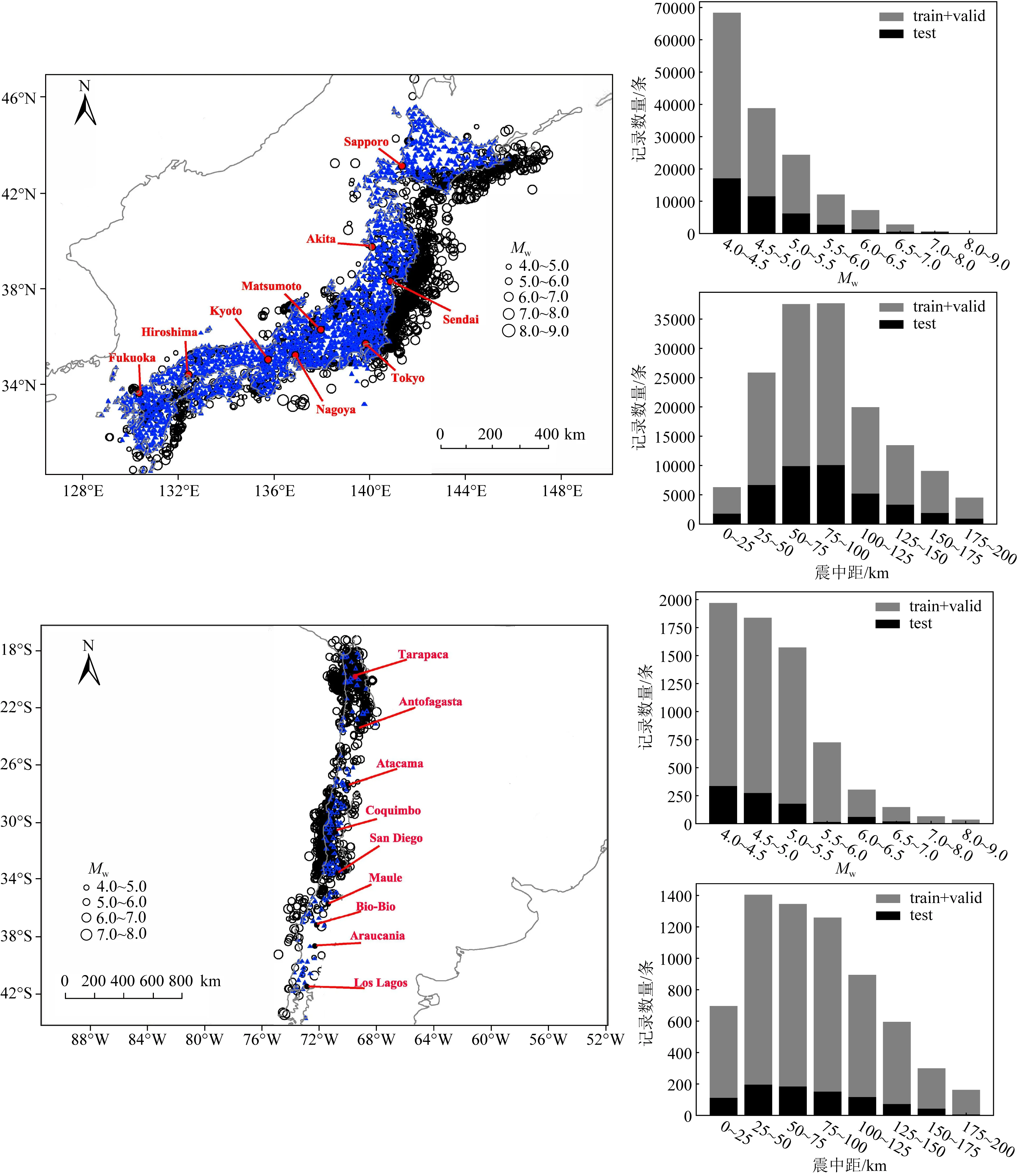
图1 地震数据的分布和数量统计(蓝色三角形为监测台站;黑色圆圈为地震事件)
为测试CNN方法在日本和智利之外地区的震级估算效果(泛化能力测试),按前述数据筛选和处理方法,建立泛化测试数据集(表1):从美国CESMD(Center for Engineering Strong Motion Data)随机下载了加利福尼亚州的14次4~7.1级地震的140条竖向加速度记录;不限定最大震源距,从新西兰GeoNet(Geological Hazard Information for New Zealand) 随机下载了14次4~7.8级地震的620条竖向加速度记录(其中震源距25~200 km的记录502条,200 km以上的118条).
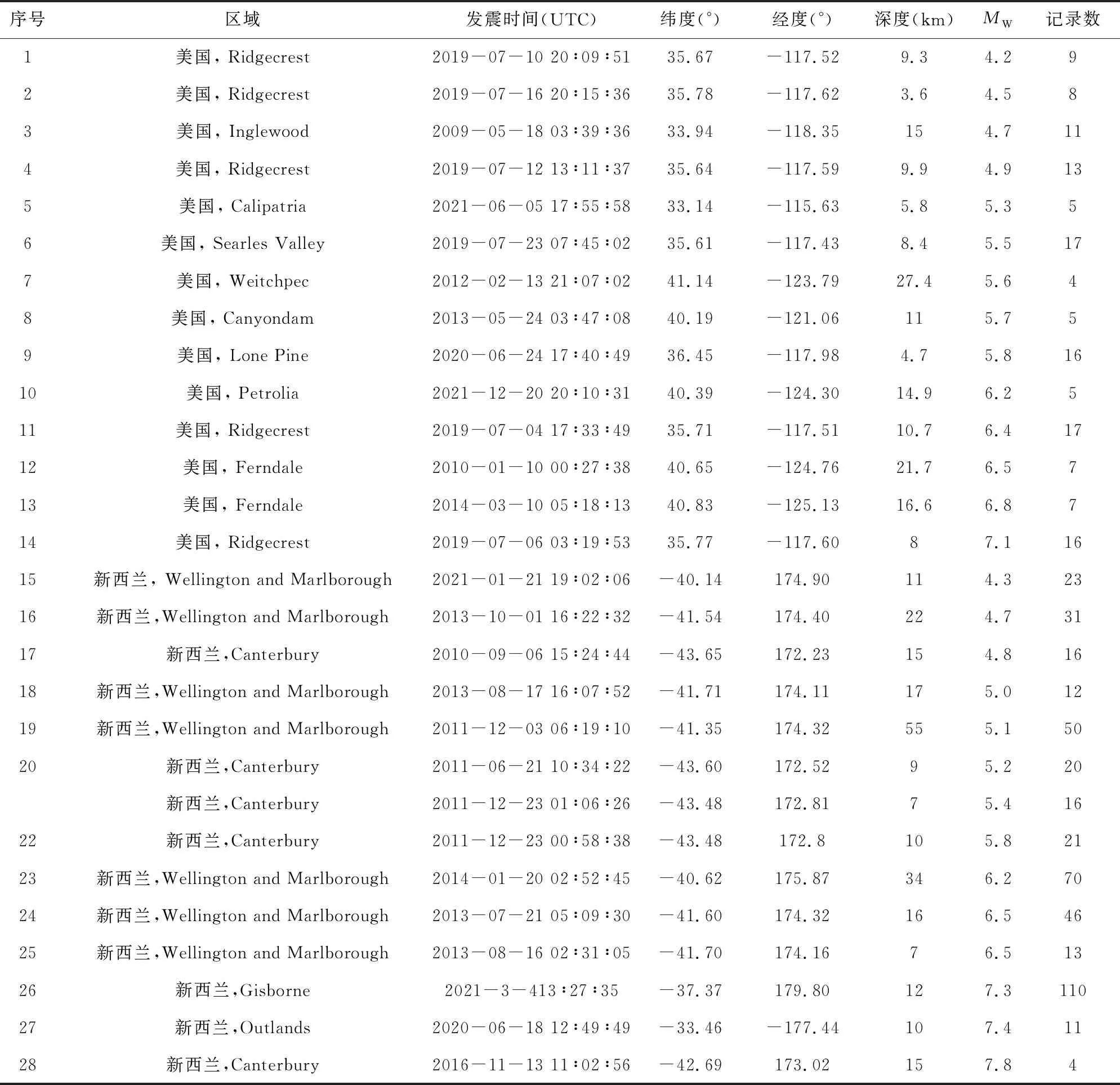
表1 泛化测试数据集
2 深层卷积神经网络估算震级
CNN方法是一种基于卷积计算的多层前馈神经网络,是当前应用最为广泛的一种深度学习方法.关于CNN方法的基本原理,在文献(吴易智等,2021)中可以找到详细的描述,这里就不再介绍.需要通过训练数据集和验证数据集的反复计算依据经验确定.本研究中CNN方法的层级架构如图2所示,包括主输入层、隐藏层、辅助输入层、全连接层和输出层.主输入层为一维数组结构,用于接收单个台站的竖向初至地震波(加速度数据).隐藏层共有10层,每层由卷积层、激活函数层、批量归一化和池化层组成,用于从初至地震波中提取与震级最为相关的特征.在各隐藏层中:卷积层的卷积核个数如表2所示,卷积核大小为1×2,卷积运算步长为2,填充模式为“same”;激活函数层采用ELU函数(Clevert et al., 2015);隐藏层的批量归一化采用z-score法(标准分数法),以避免过拟合的情况(Ioffe and Szegedy, 2015);批样本大小影响模型的训练效果和速度,批样本越大需要的GPU内存越大,根据多次试算结果以及GPU计算效率(NVIDIA RTX2080Ti 11G),最终选择批样本为256(批样本取32、64、128和256时,验证数据集的震级估算效果对比,如图3所示);池化层的设置如表2所示,平均池化方法(有利于保留全局波形特征)和最大值池化方法(有利于保留局部波形特征),两种池化层的步长均为2,池化核大小均为2,填充模式为“same”.辅助输入层为隐藏层自动提取的特征和辅助信息,辅助信息包括震中距、震源深度以及Vs30,用于考虑地震波在传播过程中受传播路径和场地条件的影响(Böse et al., 2012).全连接层是一个列向量,用于实现特征和辅助信息的回归计算;输出层为全连接层的回归结果(数值),即最终预测的震级.训练模型的损失函数定义为预测震级与真实震级的均方误差函数,采用Adam优化器(Kingma and Ba, 2014)进行优化训练,学习速率为0.001.
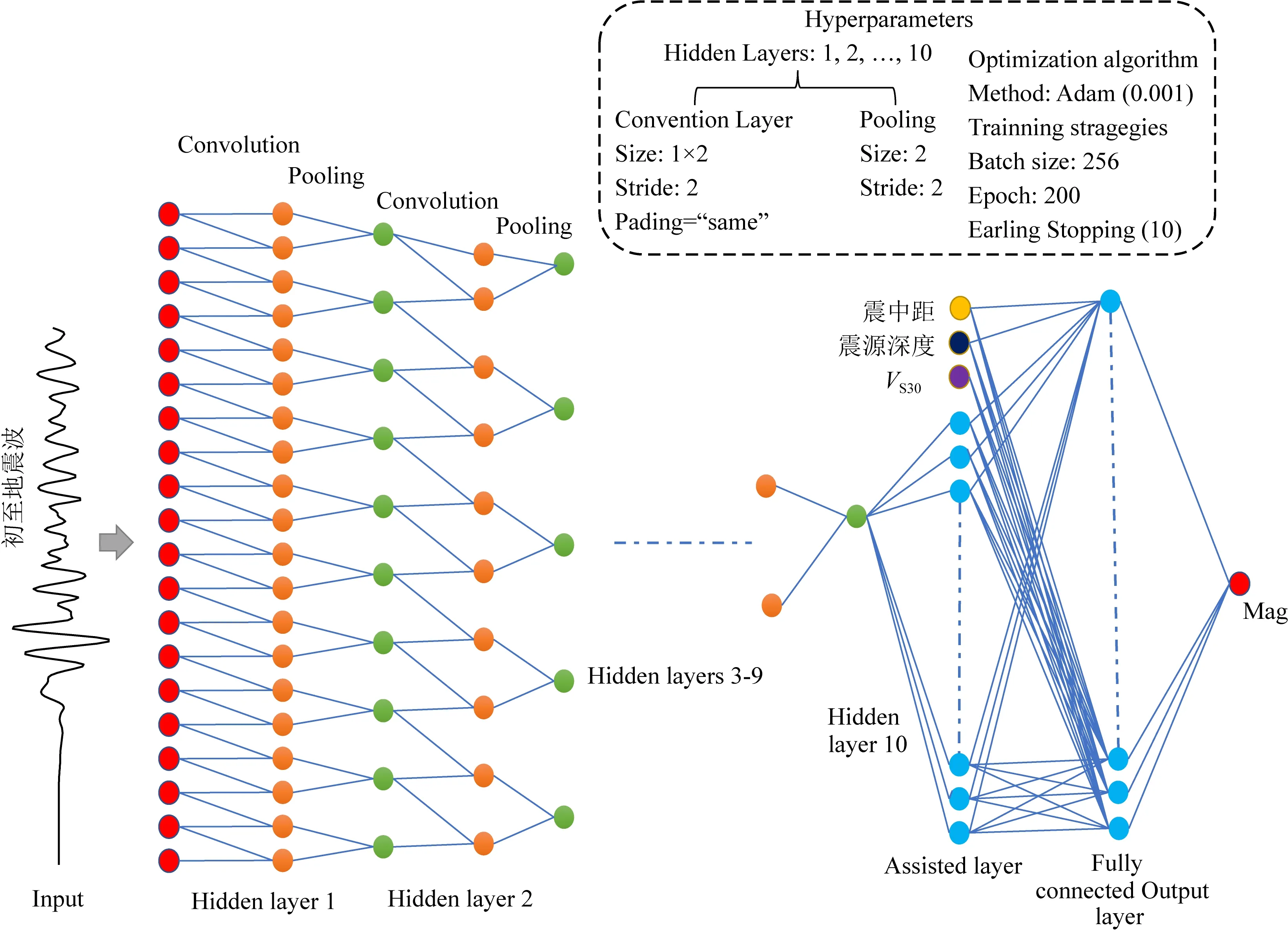
图2 CNN方法的架构和超参数

表2 卷积核和池化方法

图3 不同批样本大小时估算震级的误差标准差对比(训练数据集)
在CNN方法的训练过程中,将损失函数不在下降时的训练结果作为最终结果,例如,在输入为初至3 s 和10 s地震波时,训练数据集和验证数据集的损失函数随迭代次数的增加不断变化(图4),在前3次迭代损失函数下降幅度最大,随后损失函数变化微小,不再下降,达到稳定状态,此时,完成CNN方法的训练.
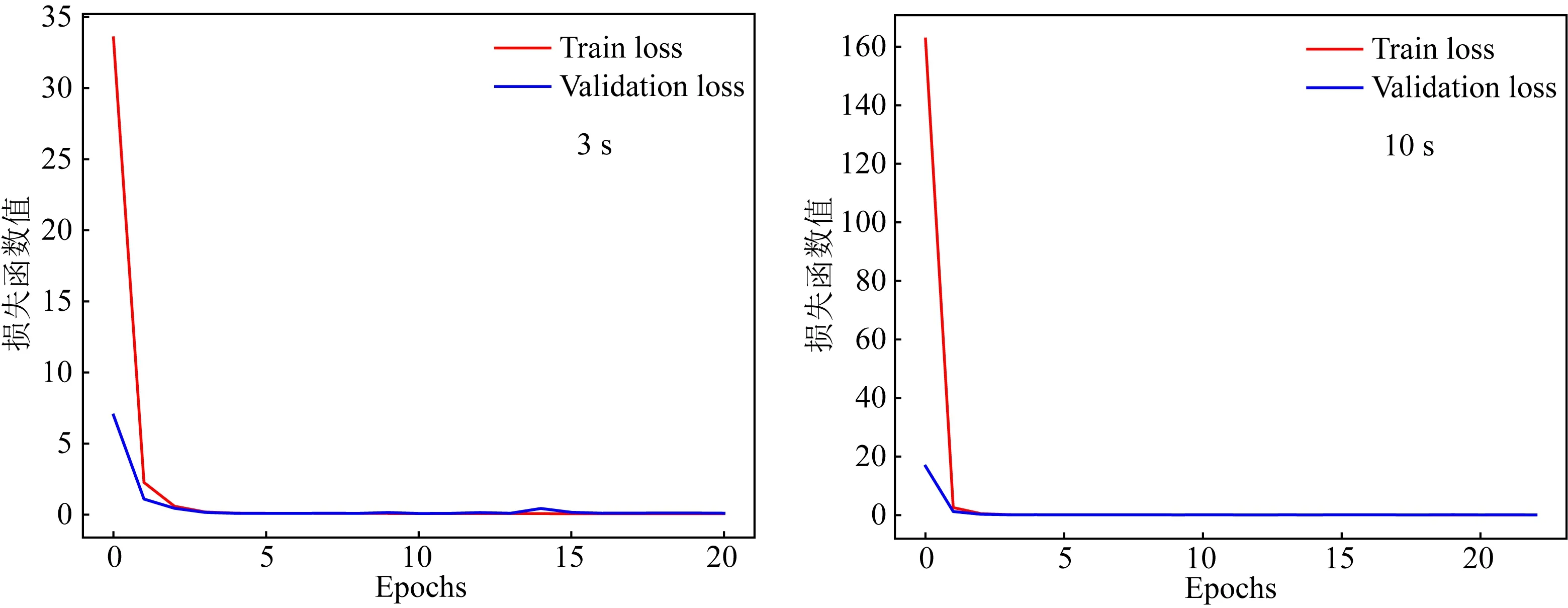
图4 初至3 s和10 s地震波时CNN迭代训练的损失函数值
3 测试
利用测试数据集和泛化数据集对CNN方法的震级估算效果进行测试,并与Pd方法进行对比.鉴于,在地震预警系统的处理流程中,会先利用P波到时和P波速度模型自动确定震中位置和震源深度(Claudio et al., 2011),再估算震级,例如我国福建地震预警系统(Zhang et al., 2016)和美国地震预警系统(Serdar et al., 2014),因此,在测试中认为震源距是已知的.选用Pd方法的原因是,多数研究表明Pd方法估算震级的准确性明显优于其他参数方法(Li et al., 2017; Nazeri et al., 2017; Leyton et al., 2018; 王延伟等, 2020),并且已被广泛应用于地震预警系统(Hsiao et al., 2009; Zhang et al.,2016; Kohler et al.,2018).Pd方法估算震级的经验公式如下:
Mag=algPd+blgΔ+c,
(1)
其中Mag是震级,Pd是初至P波的位移幅值,Δ是震源距,a、b、c是拟合系数.
地震预警的震级估算是一个随着初至地震波时长增加不断更新的过程,一般要求P波到达3 s后,随着初至地震波时长的持续增加,不断更新估算震级(Wu and Zhao, 2006; Kanamori, 2005; Peng et al., 2017).初至3~10 s地震波时,Pd与震级的经验公式(1)由训练数据集和验证数据共同得到,如表3所示.
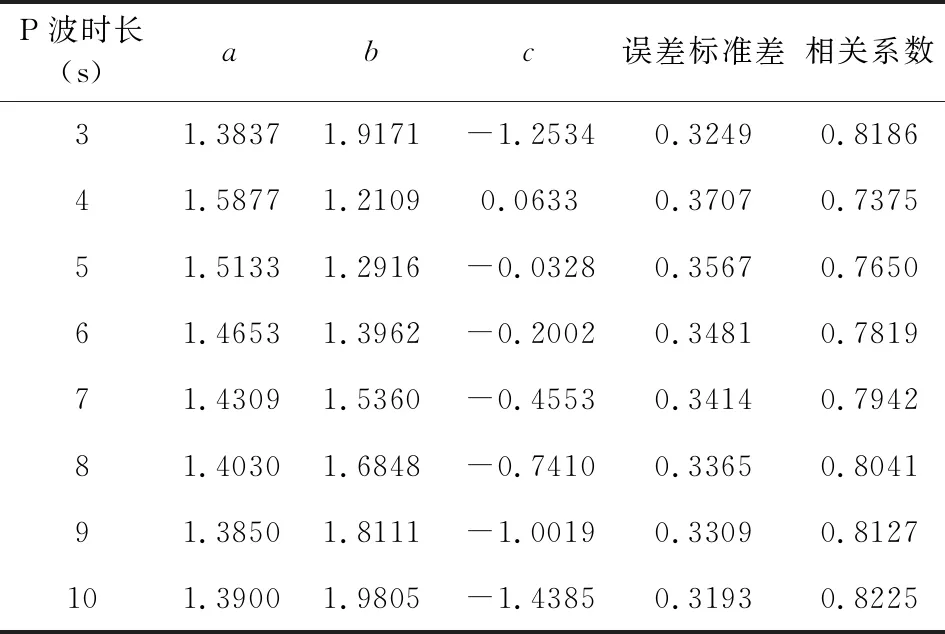
表3 初至3~10 s地震波时拟合系数表
3.1 初至3 s的P波时,测试数据集的震级估算效果
鉴于多数研究(Wu and Zhao, 2006; Kanamori, 2005; Peng et al., 2017)和已建地震预警系统(Hsiao et al., 2009; Cuéllar et al., 2014; Zhang et al.,2016; Parolai et al.,2017)表明利用初至3 s 的P波估算震级可以较好地兼顾地震预警的时效性和准确性,因此,需要着重分析初至3 s 的P波时,CNN方法和Pd方法估算震级的结果.图5是CNN方法和Pd方法估算震级的误差分布,图中的散点表示每条记录估算震级的误差,红色虚线表示±0.5个单位震级,准确率定义为误差在[-0.5,+0.5]的记录数与记录总数的比.从误差的定性分布看:无论是日本地震记录还是智利地震记录,CNN方法估算震级的误差都比Pd方法更明显地集中在零值附近,且更多地分布在[-0.5,+0.5]之内;在日本地震记录的误差分布中(图5a和图5b),CNN方法和Pd方法都表现出对约6.5级以上地震的震级估算偏小,对9级地震的估算偏小尤为明显,这使得6.5~9级范围内的准确率远小于4~6.4级范围内的准确率,这种偏小的情况与多数研究的震级饱和问题(利用初至3 s P波估算6.5级以上地震的震级偏小)是相一致的(Kanamori, 2005; Wu and Zhao, 2006; Zollo et al., 2006; 王延伟等,2020);在智利地震记录的误差分布中(图5c和图5d),由于6.5级以上的地震事件只有2次(6.7级和7.0级),无法判断震级饱和的情况.从误差的定量结果看:在日本地震记录的误差分布中(图5a和图5b),CNN估算震级的误差均值和误差标准差均远小于Pd(CNN方法分别为0.0861和0.3516,Pd方法分别为-0.0977和0.579),在4~6.4级范围内,CNN方法估算震级的准确率是Pd的1.5倍(CNN方法为90.27%,Pd方法为62.26%);在6.5~9级范围内,即便出现震级饱和问题,CNN方法估算震级的准确率仍是Pd方法的1.2倍(CNN方法为48.11%,Pd方法为42.51%);在智利地震记录的误差分布中(图5c和图5d)),CNN方法估算震级的误差均值和误差标准差均远小于Pd方法,在4~6.4级范围内,CNN方法估算震级的准确率是Pd的1.5倍(CNN方法为87.69%,Pd方法为60.67%).前述日本地震记录和智利地震记录的测试结果一致表明,CNN方法估算震级的误差均值、误差标准差和准确率均大幅优于Pd方法.

图5 初至3 s 的P波时估算震级的误差分布
3.2 不同时长初至地震波时,测试数据集的震级估算效果
当初至地震波时长从3 s增加到10 s时,测试CNN方法和Pd方法持续估算震级的效果.图5为CNN方法和Pd方法估算震级的误差标准差随初至地震波时长的变化:在日本地震记录的结果中(图6a),随着初至地震波时长的增加,CNN方法的误差标准差逐步减小且始终明显小于Pd方法的误差标准差,值得注意的是,CNN方法在3 s时的误差标准差(0.3516)仍小于Pd方法在10 s时的误差标准差(0.4118);在智利地震记录的结果中(图6b),随初至地震波时长的增加,CNN方法的误差标准差表现出与日本地震记录(图6a) 相似的变化趋势,始终远小于Pd方法,并且在3 s时的值(0.378)小于Pd方法在10 s时的值(0.522).
图7为CNN方法和Pd方法估算震级的准确率随初至地震波时长的变化.日本地震记录的结果中:在4~6.4级范围内(图7a),随着地震波时长的增加,CNN方法的准确率由90.27%提高到94.51%,Pd方法的准确率由62.26%提高到76.60%,CNN方法的准确率始终是Pd方法的1.2~1.4倍,特别是CNN方法在3 s时的准确率(90.27%)甚至远高于Pd方法在10 s时的准确率(76.60%);在6.5~9级范围内(图7b),CNN方法的准确率由48.11%提高到78.31%,Pd方法的准确率由42.51%提高到69.62%,CNN方法的准确率在各时刻始终比Pd高约7%.智利地震记录结果中:在4~6.4级范围内(图7c),随着地震波时长的增加,CNN方法的准确率由87.69%提高到90.82%,Pd方法的准确率由60.67%提高到71.35%,CNN方法的准确率始终是Pd方法的1.3~1.4倍,CNN方法在3 s时的准确率(87.69%)远高于Pd方法在10 s时的准确率(71.35%).
从误差的分布可以看出(图8,以4 s, 6 s, 8 s, 10 s的结果为例),随着地震波时长的增加,CNN方法和Pd方法都改善了6.5级以上地震的震级饱和问题.当初至地震波时长在6 s以上时,二者都较好地估算了4~7.4级地震,仅对7级、8级和9级地震的震级估算明显偏小.结合6.5级以上地震的准确率来看,CNN方法对震级饱和问题的改善优于Pd方法.
3.3 泛化数据集的震级估算效果
在前述测试中,测试数据集和训练数据集都是采用同一个国家的地震记录,而泛化数据集是由美国加利福尼亚州地区和新西兰的强震记录组成,这两个区域的地震记录没有用于训练CNN方法,也未被用于拟合Pd方法的经验公式(1).考虑到误差随震级的分布可以最为详细地展示震级估算结果,这里仅给出CNN方法和Pd方法的误差分布图(图9,以3,4,6,10 s的结果为例).从图9中可以看出:CNN方法估算震级的误差均值、误差标准差和准确率远好于Pd方法的结果,比测试数据集(图5和图6)的结果略差;从6.5~7.8级的误差分布和准确率来看,CNN方法的震级饱和现象没有Pd方法明显.

图6 初至3~10 s地震波时CNN和Pd估算震级的误差标准差对比
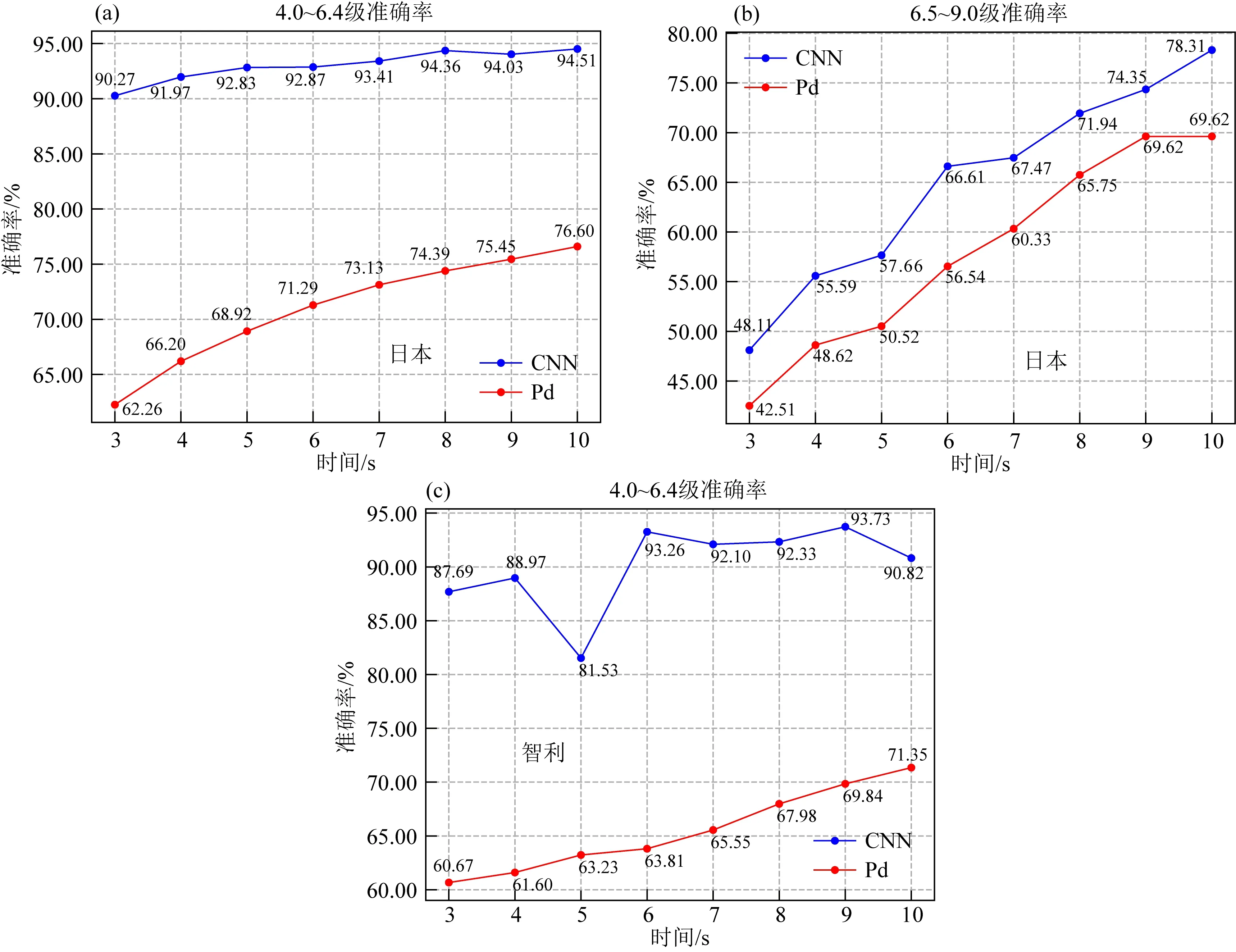
图7 初至3~10 s时CNN和Pd方法准确率随时间变化趋势对比
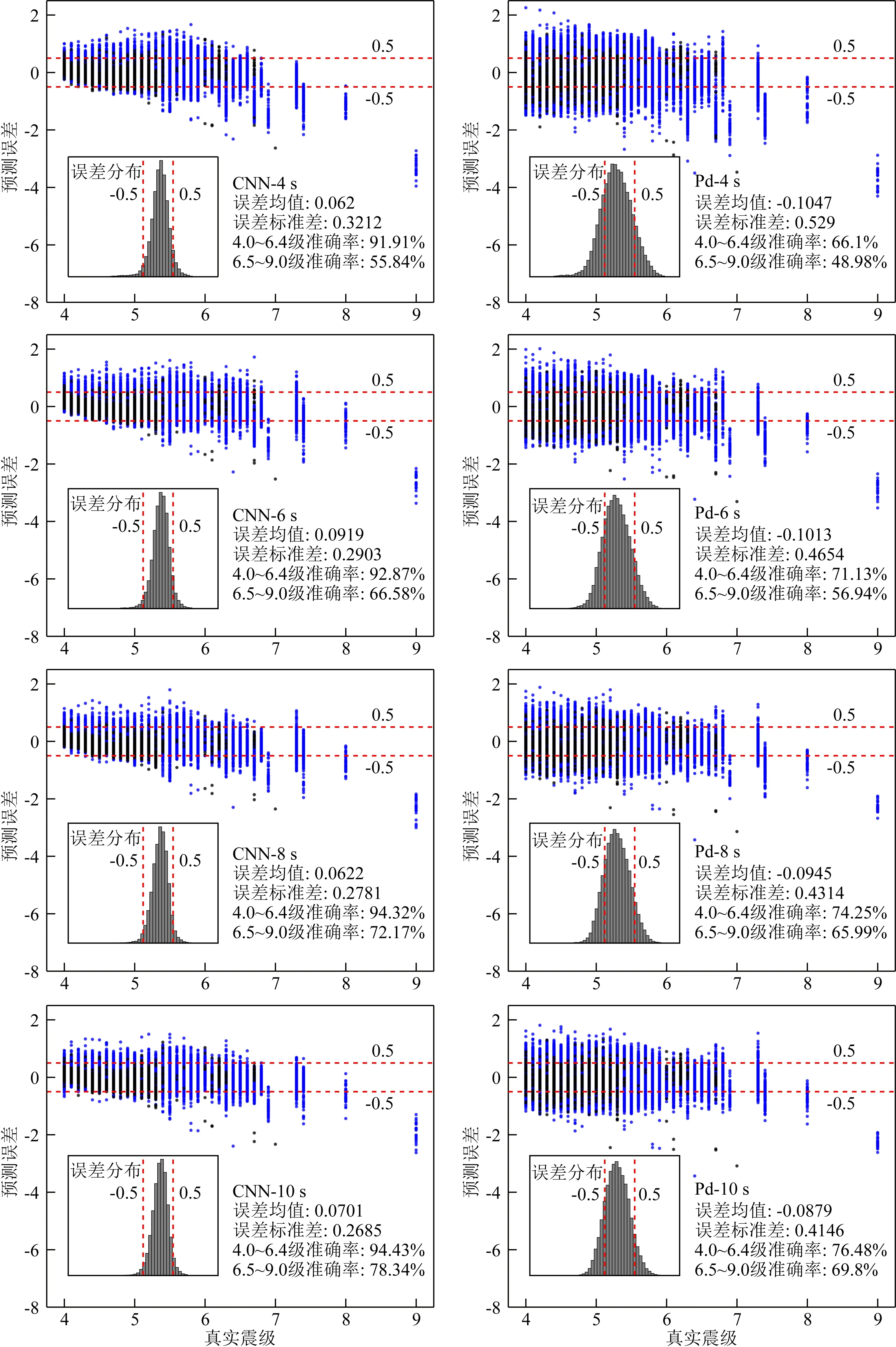
图8 初至4, 6, 8, 10 s时估算震级的误差分布(蓝色为日本记录;黑色为智利记录;误差均值、误差标准差和准确率是由日本地震记录和智利地震记录共同计算得到)
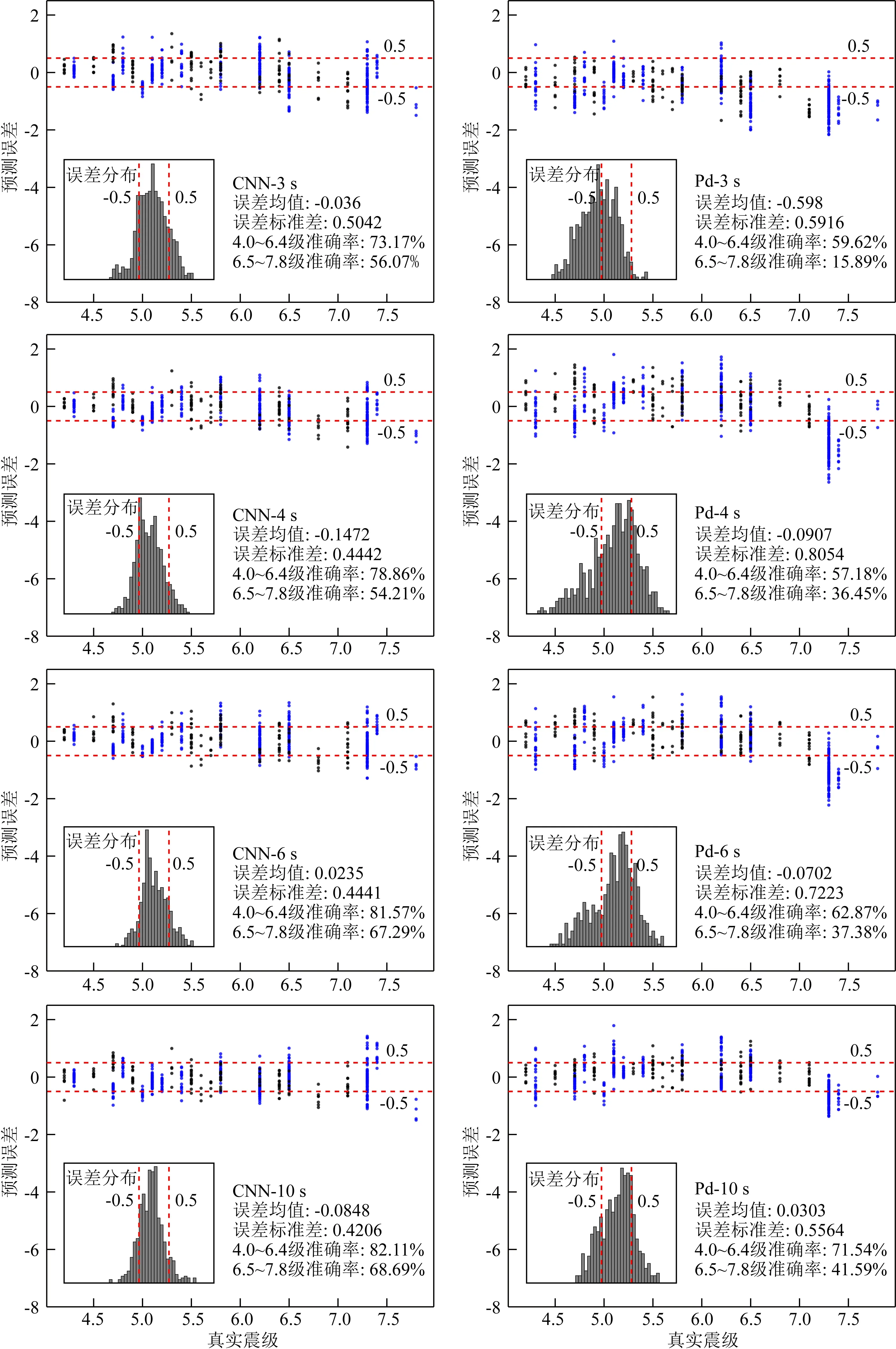
图9 初至3, 4, 6, 10 s时估算震级的误差分布
地震预警系统越快速准确地确定震级,就可以为预警区域争取到越多的应急反应时间,因此,最先触发的少数几个监测台站的震级估算效果极为关键.为此,需要进一步对比距离震中最近的2个、3个和 4个监测台站的震级估算效果.取最先触发的2个、3个和 4个监测台站估算震级的平均值作为估算震级,对比估算震级的准确率(图10)和误差分布(图11),可以看出:随着初至地震波时长的增加,CNN方法的准确率不断增大(误差分布大多在±0.5个单位震级内),而Pd方法的准确率比较不稳定(误差分布总体偏大或者偏小);在相同初至地震波时长输入时,CNN方法的准确率始终高于Pd方法,即便2个监测台站采用CNN方法的准确率也总体好于3个和4个台站的Pd方法;无论是CNN方法还是Pd方法,3个和4个监测台站的准确率较为接近,并且总体好于2个监测台站.
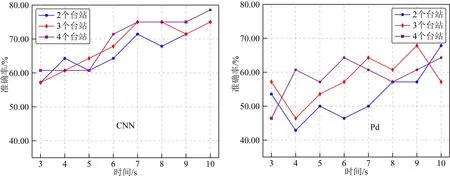
图10 最先触发的2个、3个和4个台站估算震级准确率

图11 最先触发的2个、3个和4个台站估算震级的误差分布
4 讨论
前述测试结果表明,无论是在初至3 s的P波时,还是在初至地震波从3 s持续增加到10 s的过程中,CNN方法估算震级的误差均值、误差标准差和准确率始终显著优于Pd方法.CNN方法优于Pd方法的主要原因在于:Pd方法是根据人的经验和认识得到的,即在同一观测点震级越大地表变形越大(相同震源距时),Pd仅能代表初至地震波中与震级相关的某一方面特征;CNN方法将初至地震波作为输入,将震级作为输出,以端到端(“黑箱”)方式,避免了人的主观因素对特征提取的干预,最大化地保留了与震级相关的重要特征.
与目前已有的基于深度学习方法相比(Lomax et al.,2019; Mousavi and Beroza, 2020; Van Den Ende and Ampuero, 2020; Zhang et al., 2021),本文的CNN方法在4个方面表现出了优势:(1)利用了更短的初至地震波,实现了更大震级范围的估算,可以满足地震预警时效性和准确性的要求;(2)更简化的输入数据,本文仅利用了初至竖向地震波,且未对数据进行任何滤波处理,而已有深度学习方法都采用了滤波后的初至三个分向地震波作为输入,滤波参数选择不当往往会引起信息的丢失,例如Mousavi和Beroza(2020)采用1.0~40.0 Hz带通滤波,Van Den Ende和Ampuero(2020)采用0.1~8 Hz带通滤波,Zhang等(2021)采用0.5~9 Hz带通滤波,此外,初至几秒的竖向地震波比两个水平向地震波具有更好的信噪比,在数据质量上更有优势;(3)考虑了场地条件,在本文CNN模型的隐藏层中设计了辅助输入层,通过该层可以引入场地条件参数,已有深度学习方法并不能利用场地条件的信息;(4)更合理的神经网络模型,本文设计的CNN模型将震级估算作为回归问题来解决,输出是震级数值,而已有深度学习方法将震级估算作为分类问题(Lomax et al.,2019; Van Den Ende and Ampuero, 2020; Zhang et al., 2021),输出是不同震级的概率,需要根据概率阈值来确定震级,阈值设置会影响震级估算效果.

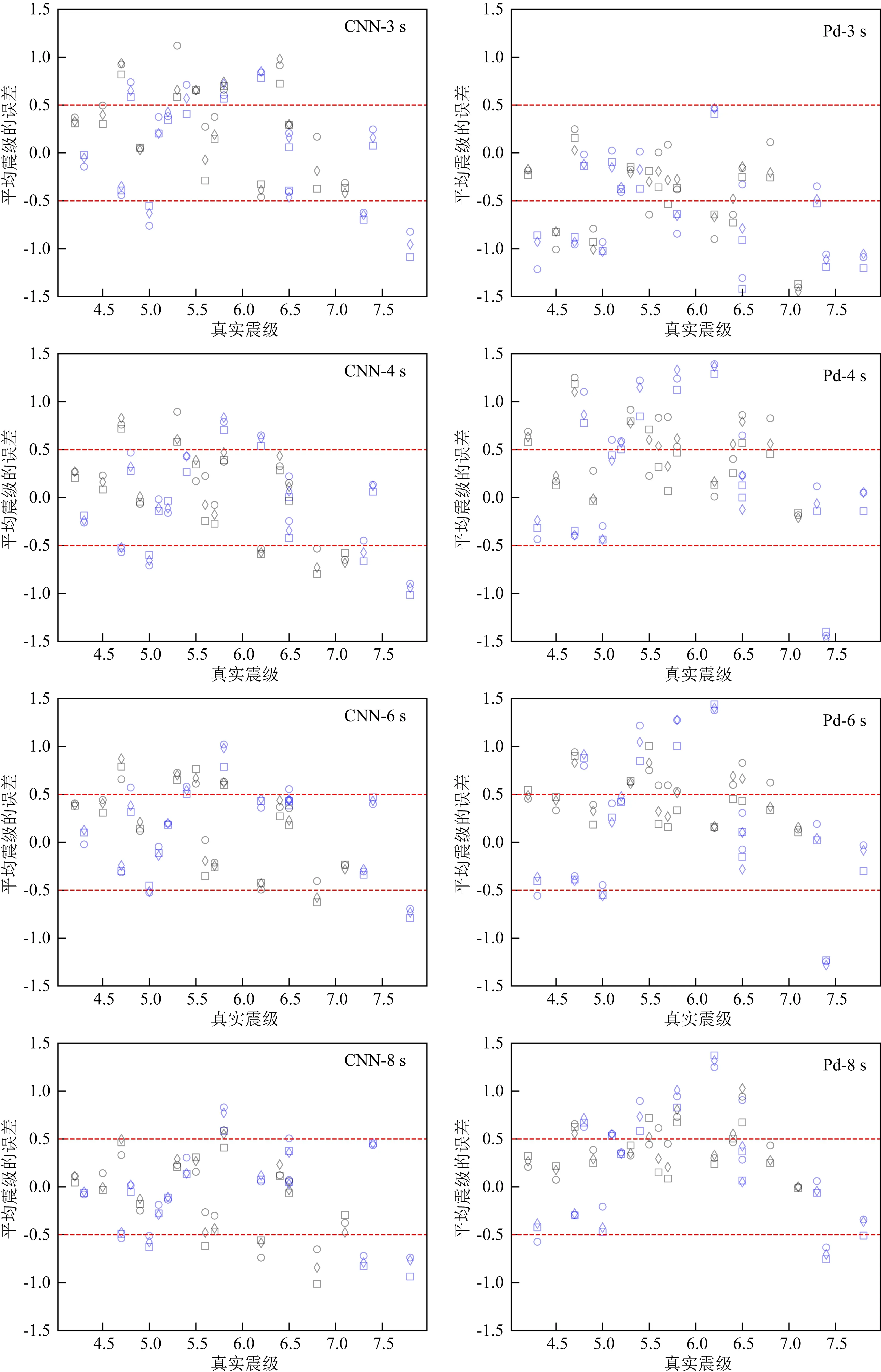
(图11续)
在泛化数据集的测试中,CNN方法表现出了较好的震级估算效果,但并未达到测试数据集的测试效果.其原因在于,训练数据集中没有泛化数据集所属区域的数据.这说明CNN方法在估算震级时具有一定的区域特性,这种区域特性也普遍存在于传统震级估算方法中(金星等,2012;彭朝勇等,2013;Li et al., 2017;王延伟等, 2020),不同的是,CNN方法因为自动提取到了与震级更为相关的特征,而比传统震级估算方法受区域特性影响小.CNN方法的区域特性,可以通过在训练数据集中增加本地区的地震记录来解决,这一点可由智利地震记录的测试结果证明.
本文提出的CNN方法以端到端的方式实现了震级的估算,其关键优势是特征提取的过程避免了人的主观因素干预,但同时也带来3个疑问值得深入研究:(1)CNN方法的层级架构和超参数决定了CNN方法的特征提取能力,然而,二者的设置并没有明确的规律和依据,只能通过反复试算凭经验来设置,是否存在有效的优化规律?(2)CNN方法从初至地震波中自动提取到的特征是未知的,这些特征能否像图像识别领域(Zeiler et al., 2011)进行解析?(3)小地震的记录在数量上远多于大地震记录,通过对大地震的记录进行数据增强(Shorten and Khoshgoftaar, 2019),是否可以解决震级饱和问题?未来的研究希望聚焦于这三个问题,从而进一步改善CNN方法估算震级的效果.
5 总结
为改善地震预警中的震级估算效果,避免人为因素对初至地震波特征提取的影响,提出具有10层隐藏层架构的“端到端”CNN方法.该方法将单台站的初至竖向地震波作为主输入,震中距、震源深度和Vs30作为辅助输入,震级作为输出,通过从初至地震波中自动提取与震级相关的特征实现震级估算.从日本和智利收集约17万竖向强震动记录,建立了训练数据集,验证数据集和测试数据集.通过反复的训练和验证确定了CNN的架构和超参数设置.利用测试数据集检验CNN方法的震级估算效果,利用美国和新西兰的28次地震事件测试CNN方法泛化能力,并与当前广泛使用的Pd方法进行对比.结果表明,当初至3 s至10 s地震波时,CNN方法比Pd方法可以更快更准地估算震级,并且受区域特性影响更小.CNN方法极大地提高了震级估算的准确性和时效性,其从初至地震波中提取与震级相关特征的能力远高于人工方式,这种特征提取能力对于地震预警和地震学其它问题研究具有重要的参考价值.
致谢审稿专家为本文提出了宝贵的意见,在此衷心感谢!感谢本文编辑认真、辛勤的付出!感谢日本防灾科学技术研究所(NIED)、智利SIBER-RISK、美国CESMD和新西兰GeoNet为本文研究提供强震动数据,以及NIED F-net和Global CMT提供矩震级.
