角度域广义Radon变换多参数非迭代线性反演
2023-01-10栗学磊魏彦杰欧阳威
栗学磊, 魏彦杰, 欧阳威
1 中国科学院深圳先进技术研究院, 深圳 518055 2 中国科学院精密测量科学与技术创新研究院, 武汉 430077
0 引言
基于Born近似的线性反演方法是一类当前流行的定量化地震成像和反演方法,可对物性反演和岩性解释提供有效的支持,比如最小二乘偏移(LSM)和广义Radon变换(GRT)反演.LSM在近20年一直是非常活跃的研究领域(Stanton and Sacchi, 2017),它在提高分辨率和压制脚印等方面比常规偏移成像方法具有明显优势(刘国章等,2020;刘玉敏等,2021).LSM通过迭代偏移和反偏移算子,拟合重建数据与原始数据,来求解基于Born近似的扰动参数.Nemeth等(1999)实现了最小二乘 Kirchhoff 偏移方法,压制了由于数据不完整导致的成像脚印.当前,LSM偏移算子已扩展到双程波动方程(Dai et al., 2012)、多震源偏移(Dai, 2012)、弹性多参数偏移(Duan et al., 2016; Ren and Li, 2020)、成像域最小二乘偏移(IDLSM)(Fletcher et al., 2016; Guo and Wang, 2020).
然而,LSM仍然处于试验探索阶段(杨勤勇和段心标, 2018),面临多种问题有待解决.当前LSM存在两个主要问题难以避免:(1) LSM需要迭代执行偏移和反偏移算子,迭代计算成本过高;(2) LSM要求背景模型是准确的,否则迭代收敛性较差.这两个问题导致LSM在大规模应用中难以执行.
为了解决背景模型依赖问题,同时减少迭代次数,扩展域Born伪逆算子在近期获得了发展(Symes, 2008; ten Kroode, 2012; 刘玉金和李振春, 2015; Hou and Symes, 2015; Chauris and Cocher, 2017),且当前已推广到2D变密度声波介质(Farshad and Chauris, 2020).该伪逆Born算子是在地下偏移距域逆时偏移(RTM)的基础上,近似建立的一种地震数据与扩展域模型之间的转换算子.扩展域模型与地震数据维度相同,可以保存大部分的原始地震数据信息.因此,该扩展域方法能够精确重建原始地震数据,即使背景模型是错误的.同时,该扩展域模型可通过Radon变换提取角度域信息.
扩展域Born伪逆算子的主要弊端在于计算量明显高于常规RTM.其计算成本与地下偏移距方向的离散采样数量线性相关.如果背景模型是已知且准确的,该离散采样数量可以减少,计算成本可以缓解(Hou and Symes, 2015).然而,对于3D模型情况,该扩展域方法计算耗时将是巨大的,因为3D中的地下偏移距会在x和y方向同时离散采样,采样数量是2D模型的平方.因此,该方法也不适合未来3D大规模推广.
GRT反演是另一种基于Born(Kirchhoff)近似的线性反演方法.与LSM相比,GRT反演是一种非迭代高效的线性反演方法,且已推广到弹性多参数反演.Beylkin(1984, 1985)通过构造 Beylkin 行列式建立了声波单参数GRT逆变换算子理论.Miller等(1987)进一步分析了GRT的反演特征与应用.Bleistein(1987)基于Kirchhoff近似将GRT推广到反射系数反演多参数.之后,多参数GRT反演方法获得发展.Beylkin和Burridge(1990)发展了声波和弹性多参数GRT反演.Ikelle等(1992)进一步分析了阻抗和速度扰动参数反演分布情况.后来多参数 GRT 反演推广到弹性各向异性介质(de Hoop et al., 1994, 1999; de Hoop and Bleistein, 1997; Burridge et al., 1998; Ursin, 2004).另外,Protasov和Tcheverda(2011)结合GRT和高斯束方法发展了真振幅成像.为解决大扰动参数问题,基于GRT的双散射反演方法获得了发展(Ouyang et al., 2015, 2017; Ouyang and Mao, 2018).
然而,在过去20年GRT反演方法并未获得充足的研究与推广.现有GRT中的多参数提取存在明显的不确定性和不稳定性问题.多参数提取算子是一N阶方阵的逆(N为提取参数数量),与散射角积分直接相关.而该散射角积分范围随方位角、倾角变化,在实际中是不确定且非唯一的.Beylkin和Burridge(1990)通过出现的最大散射角来确定散射角范围,这种方法提取的多参数往往不准确.同时,该多参数提取算子也经常不稳定.受参数数量影响,该提取算子常为病态,尤其是参数数量过多时(如三个以上).因此,利用现有多参数 GRT 反演方法获取精确和稳定的反演结果非常困难.另外,与LSM类似,现有GRT反演同样要求背景模型准确.
为解决现有线性反演方法存在的主要问题,本文提出了角度域GRT(AD-GRT)多参数反演方法(2D声波介质).角度域信息是当前地震成像与数据分析中的最有效信息(张宇, 2018),可直接应用于速度建模和AVA分析,且明显降低成像与反演的非唯一性(Xu et al., 2001).我们利用局部走时和幅值近似搭建了角度域积分变换方程,实现了原始地震数据与角度域模型之间的精确变换.与扩展域Born伪逆算子类似,该角度域模型也是一种扩展域模型,可支持精确的地震数据重建,即使背景模型不准确.角度域模型可用于提取准确的扰动多参数.不同于扩展域Born伪逆算子,AD-GRT计算耗时和常规GRT反演耗时相当.角度方向的采样点数量对AD-GRT的计算量影响微弱.为提高角度域信息的精度,AD-GRT的角度方向采样比常规角度域成像方法(Zhang et al., 2007; Tang et al., 2013)要明显密集.同时,为解决传统角度域离散方法(Xu et al., 2001)存在的幅值震荡问题,我们设计了两种有效的角度域离散分裂方法.实验验证了新提出的离散方法在提取平滑连续的角度域信息方面的优势.另外,为提高AD-GRT反演的分辨率,我们将震源子波反滤波用于反演.
1 声波广义Radon正变换
该部分回顾在2D声波介质中基于Born近似的GRT正变换.2D非均匀声波介质频率域无源波动方程可表示为:
(1)
其中p(x,ω)为点x=(x1,x3)的声波压力波场,κ(x)=1/(ρc2)为压缩率,σ(x)=1/ρ为密度倒数,c=c(x)和ρ=ρ(x)分别为波速和密度.在2D情况下,下标j=1,3.本文公式中仅对全局坐标系中的方向性下标(即x1,x3方向)执行爱因斯坦求和约定,其他上下标符号不执行求和操作.依照散射理论,如果将原始介质属性参数分解为背景参数和扰动参数,则原始波场可分解为背景波场和散射波场.所以设置参数:
σ(x)=σ0(x)+σ′(x),κ(x)=κ0(x)+κ′(x),
(2)
其中σ0和κ0为背景参数,一般是已知的,σ′和κ′为对应的扰动参数.这种情况下,原始波场可分解为:
p(x,ω)=p0(x,ω)+p′(x,ω),
(3)
其中p0和p′分别为背景波场和散射波场.假设扰动参数非常小,则散射波场以单散射为主,多散射波场可以忽略.基于声波格林函数和Born近似,散射波场线性方程可表示为:
(4)
其中,G0=G0(x,r,ω)为背景模型中的声波格林函数,且具有互易属性G0(r,x,ω)=G0(x,r,ω),r=(r1,r3)为散射波场接收点.
基于式(4),对应的2D声波GRT正变换可获取(Beylkin和Burridge, 1990).式(4)中背景波场p0与震源位置和子波有关,在此用子波与格林函数F(ω)G0(x,s,ω)代替p0(x,ω),其中F(ω)为震源子波频率域公式,对应的时间域子波用F(t)表示.如果子波为脉冲子波,则有F(ω)=1.本文中的时间和频率域(或空间和波数域)函数使用相同函数符号表示,通过函数变量具体区分.将背景模型中的格林函数表示为:
(5)
其中,s=(s1,s3)为背景波场震源点,下标s和r分别代表震源端和接收端,As和φs分别代表震源端振幅和走时,Ar和φr分别为接收端振幅和走时.基于高频近似,格林函数的空间偏导数可近似表示为:
(6)
将式(5)、(6)代入式(4),整理可得:
×F(ω)f(x,θ),
(7)
其中,f(x,θ)为一种角度域模型:
(8)
依据式(8),可以利用两个扰动参数f1和f2来线性描述f(x,θ),即:
(9)
θ=θ(s,x,r)为散射角,是s到x射线和r到x射线在x处的夹角,且满足:
θ=αs-αr,
(10)
×F(t-φs-φr),
(11)
其中,A(s,x,r)为振幅因子,其与As和Ar满足|ω|AsArκ0=isgn(ω)A(s,x,r),此处sgn(ω)为符号函数.A(s,x,r)可用几何扩散物理量表示:
(12)
其中,q2为一个动力学射线参数.ρ0和c0分别为背景密度和波速.由于常规射线理论在焦散区误差明显,本文临时忽略焦散区影响.
式(7)、(11)分别为频率域和时间域2D声波广义Radon正变换.该变换相当于角度域模型f(x,θ)到波场数据p′(r,s,t)的积分变换,此处的s和r仅分布在2D扰动区域的边界线上.理论上,f(x,θ)和p′(r,s,t)的均具有三个维度分布,因此,对应的从p′(r,s,t)到f(x,θ)的逆变换也可搭建.
2 角度域广义Radon逆变换
该部分在式(7)、(11)的基础上,建立对应的角度域广义Radon逆变换(AD-GRT),以支持从p′(r,s,t)到f(x,θ)的反向积分变换,并在此基础上实现声波多参数提取和数据重建拟合.
AD-GRT可以在Fourier变换的基础上建立起来.f(x,θ)的2D Fourier变换可写为:
(13a)
×exp[ikj(xj-yj)],
(13b)
其中,k=(k1,k3)为2D波数矢量.x和y分别为扰动点和反演点.为了在式(13b)内部组建与式(7)相同的表示形式,需要对比分析式(13b)、(7).式(7)、(13b)均包含积分项dx1dx3f(x,θ),且分别包含复相位项exp[iω(φs+φr)]和exp[ikj(xj-yj)].剩余部分分别与(r,s,ω)和dk1dk3相关.为了组建p′(r,s,ω)的逆变换,需要建立(r,s,ω)和dk1dk3之间的转换关系.基于以上分析,下面通过以下三步完成建立AD-GRT.
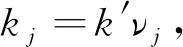
(14)
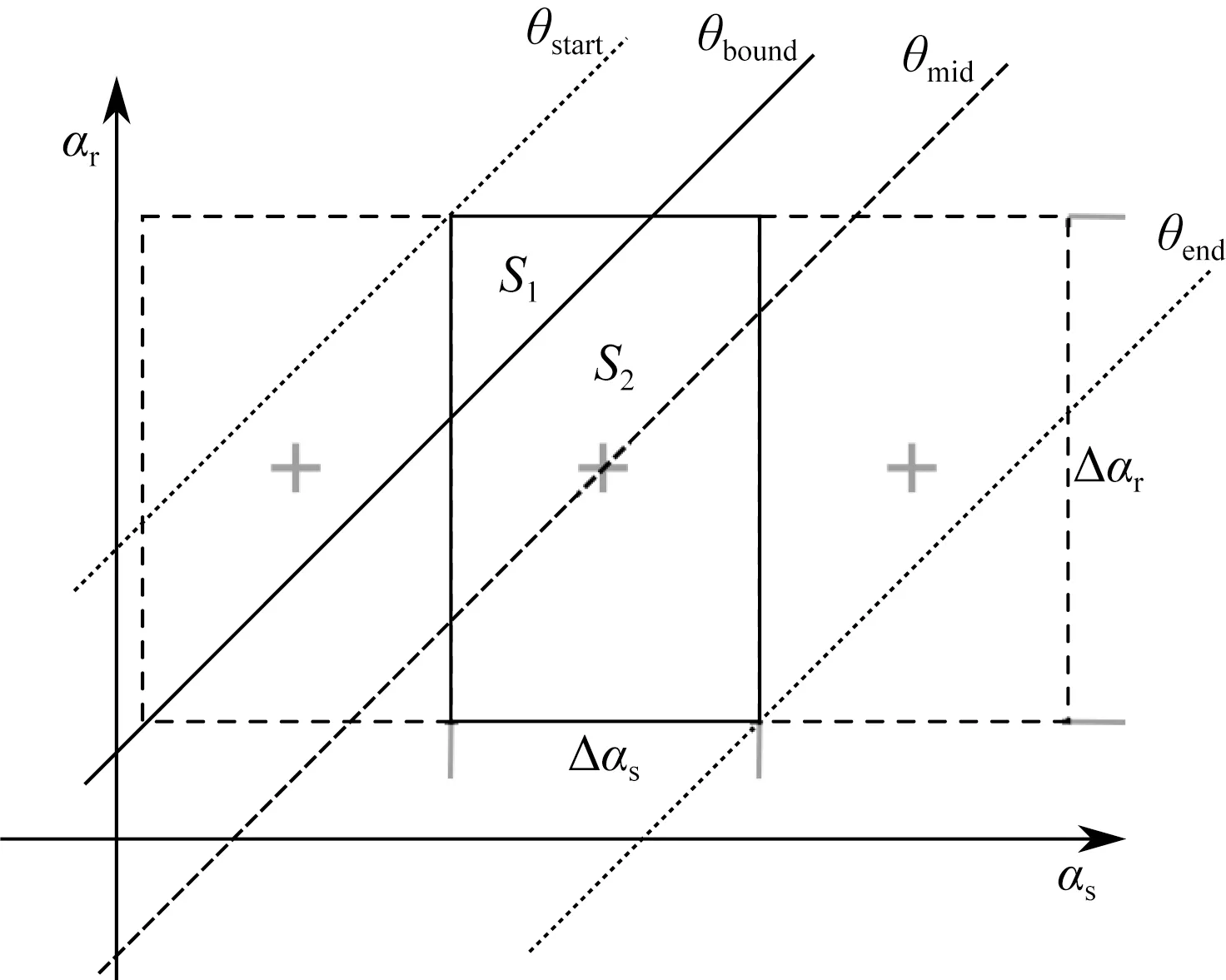
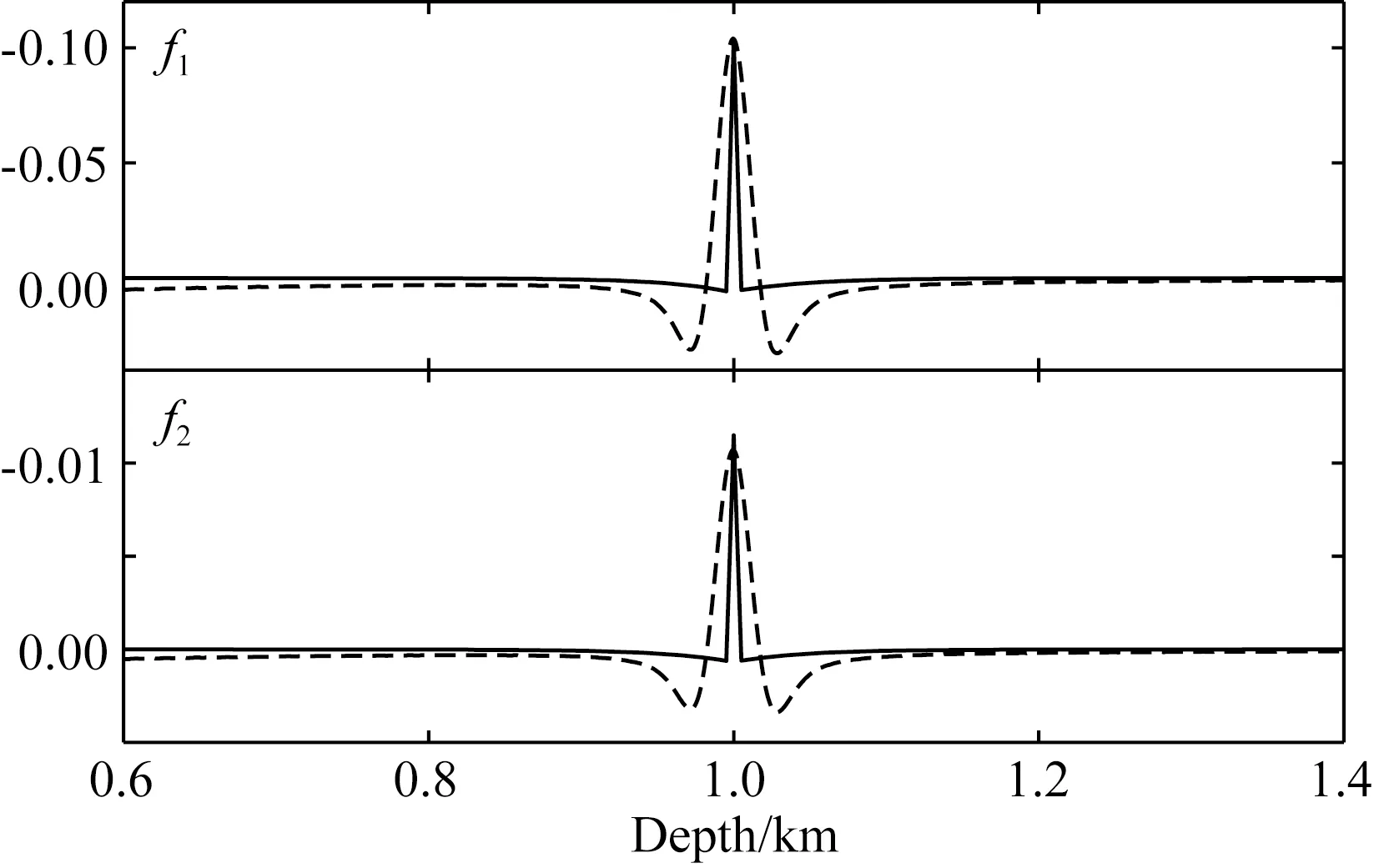
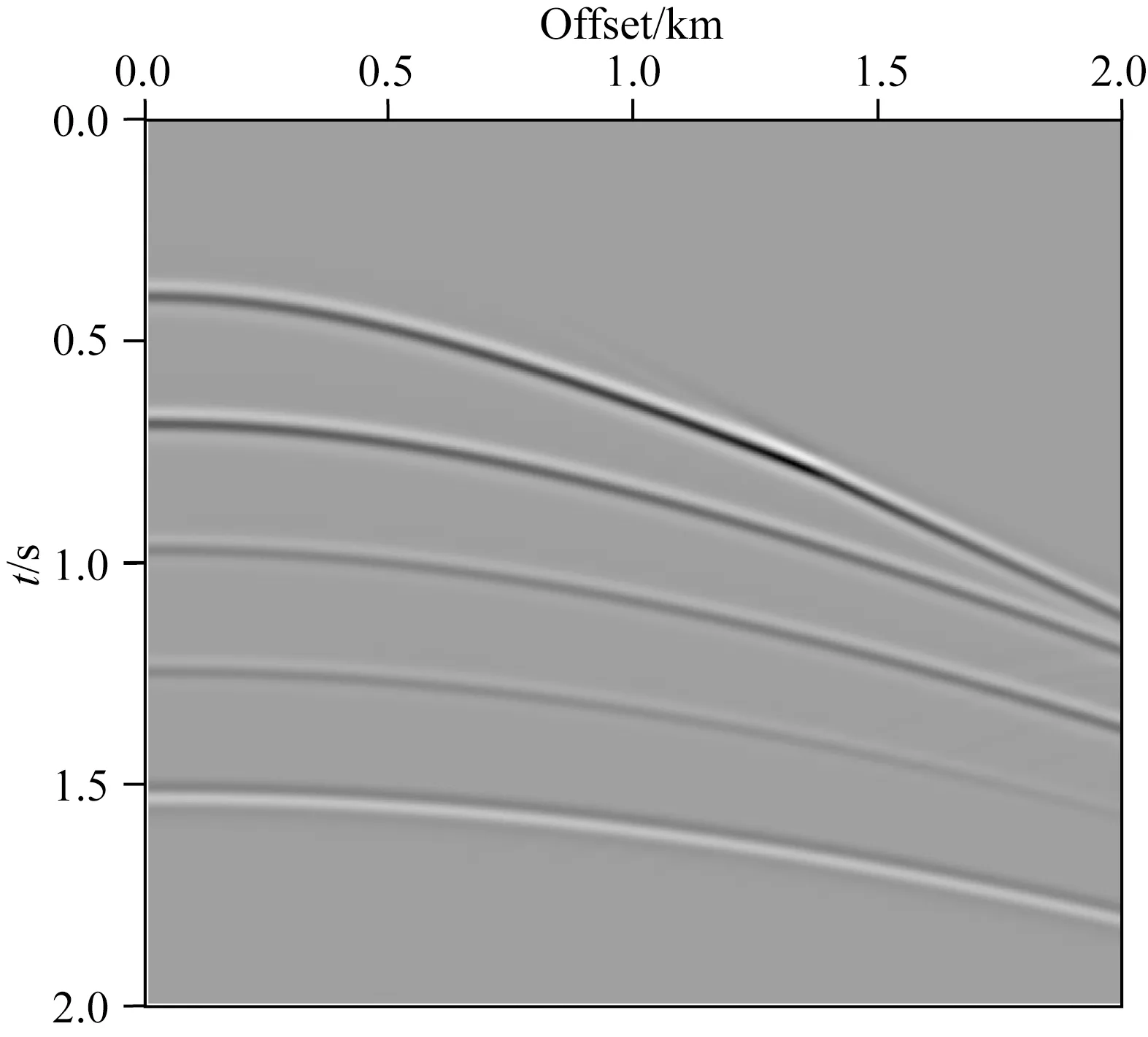
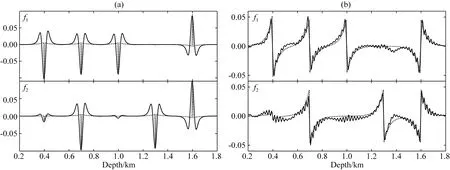
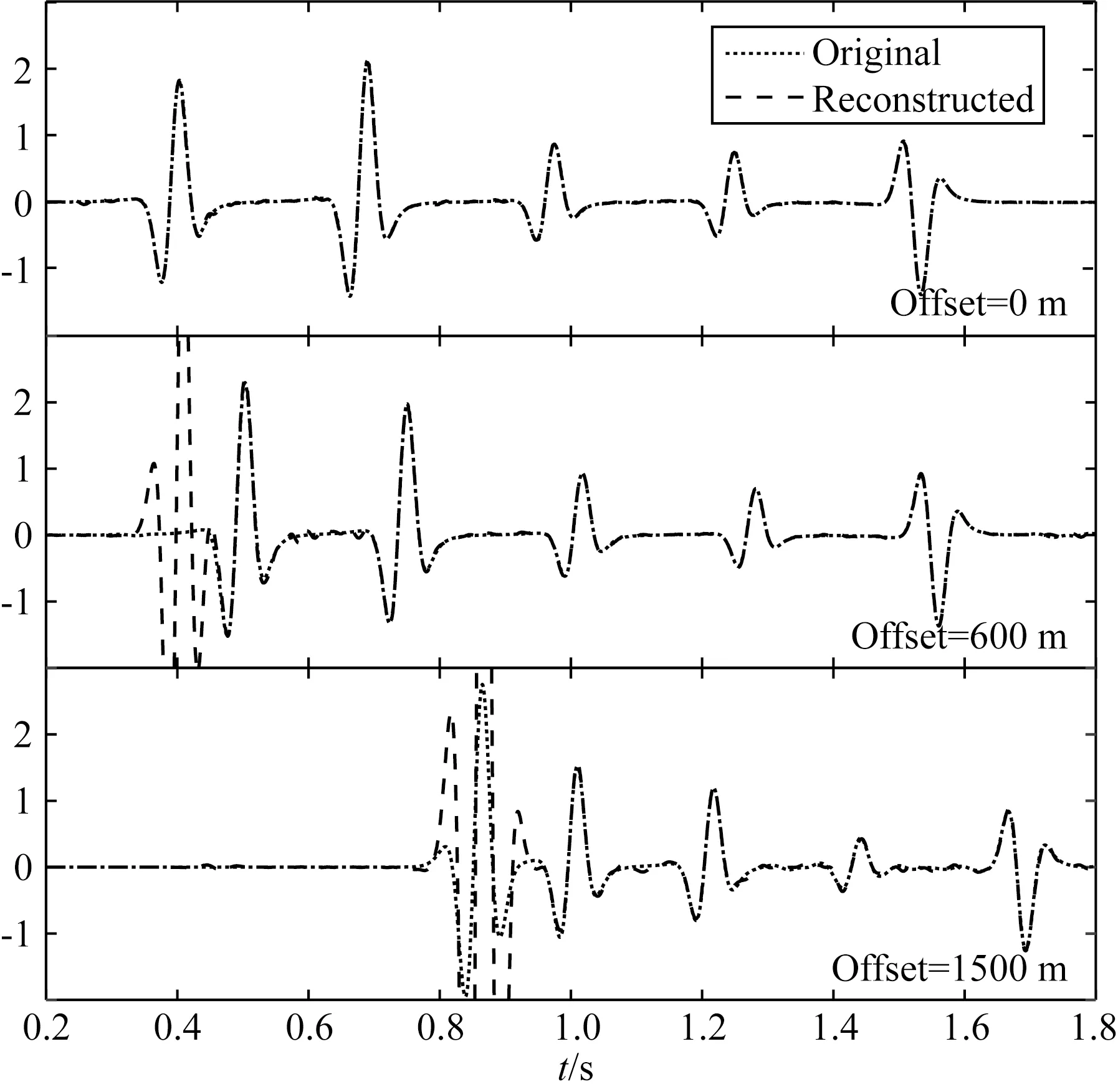
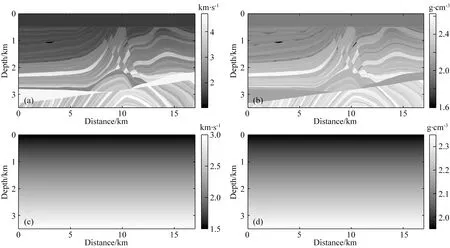
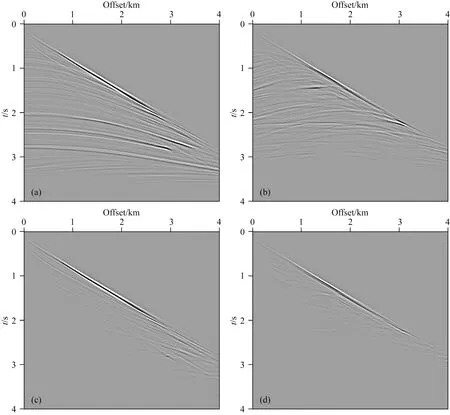
k′和νj的取值范围主要有两种有效设置,第一种为0≤k′<∞,νj分布在整个单位元,第二种为-∞ (15a) (15b) 其中psj(y)和prj(y)为慢度矢量ps(y)和pr(y)的分量.如果设置: (16) 则可得出: (17a) (17b) 由式(17a)、(17b)可知,k′/ω是慢度矢量ps+pr的模,νj是ps+pr的单位方向矢量,也是走时φs(y)+φr(y)等值线倾角. 将式(15)、(17a)代入式(14),整理可得: ×f(x,θ)exp[iω(φs(x)+φr(x))] ×exp[-iω(φs(y)+φr(y))], (18) 其中: (19) 第三,建立积分项drdsdω相关的积分表达式.式(18)现有的积分项dωdν是二维空间积分,不能直接转换到drdsdω.同时,倾角散射角坐标系(ν,θ)可以映射到边界线上的震源接收点坐标系(s,r).所以式(18)对于组建p′(r,s,ω)到f(y,θ)逆变换尚缺少散射角积分项dθ.为此,对f(y,θ)添加一层积分dθ: (20) 其中,θ0代表散射角θ的采样点.将式(18)代入式(20),可得: ×f(x,θ)exp[iω(φs(x)+φr(x))] ×exp[-iω(φs(y)+φr(y))]. (21) 在2D单位圆上,积分项满足转换dνdθ=dαsdαr,其中,αs(y)和αr(y)为可映射震源s和接收点r的方向角,且满足雅可比转换: dαs=Js(y)ds, dαr=Jr(y)dr, (22) dνdθ=Js(y)Jr(y)dsdr. (23) 将关系式(23)代入式(21),整理可得: ×Js(y)Jr(y)f(x,θ)exp[iω(φs(x)+φr(x))] exp[-iω(φs(y)+φr(y))], (24) 至此,式(24)已包含了式(7)中相关的各项积分项和复相位项.在此基础上,补充其他因子项,即可建立逆变换.假设x在y附近周围,则振幅满足局部近似: As(x,ω)≈As(y,ω),Ar(x,ω)≈Ar(y,ω). (25) 对比式(24)、(7),逆变换可建立: (26) 类似于式(11),频率域式(26)可以转换为对应的时间域方程.设定: (27) (28) 式(28)即为2D声波AD-GRT,与式(11)为对应的p′(r,s,t)和f(y,θ0)之间的积分变换.在AD-GRT建立过程中,我们在两处使用了局部近似(式(15)、(25)),只要输入数据具有较好的连续性,这种近似导致的误差是微弱的.基于反演的f(y,θ0),声波双扰动参数可以利用线性关系式(8)和最小二乘拟合方法获得有效提取,原始波场数据可以利用正变换式(11)有效重建拟合. 虽然当前已获得AD-GRT最终表达式(28),但是式中的δ(θ-θ0)并不方便直接参与计算,需要利用其他的近似插值或求和算法代替.并且,θ0离散采样点与震源s和接收点r的离散分布并不能直接对应.这给AD-GRT的精确数值计算带来了一定麻烦.为此,我们在常规角度域离散算法的基础上,设计AD-GRT的准确离散算法.角度积分表达式(20)可以近似表示为: (29) 为了解决传统角度域算法的离散问题,我们对θ相关的积分求和做进一步分析,设计合理的数值求解方案.离散后的微元满足关系式: Δαs≈JsΔs,Δαr≈JrΔr, (30) 其中Δs和Δr是炮点和接收点离散间隔,实际计算中是已知的.Δαs和Δαr分别为s和r传播到y的射线方向间隔,可通过雅克比系数Js和Jr计算求得.因此,一个(s,r)的离散采样点在y对应的是一个离散单元,单元面积大小为Δαs×Δαr.而常规算法忽略该单元面积大小,仅依靠采样点上的θ值来判断累加位置是不合理的.当采样点θ非常靠近分区边界θ0±Δθ/2时,该单元有一部分应属于θ0附近分区.这也是常规角度域计算方法出现幅值起伏震荡的主要原因. 基于以上分析,我们将分区边界θ0±Δθ/2附近的离散单元分裂为两个离散单元,并求解分裂后的两个离散单元的面积大小S1和S2.精确计算两个分裂单元大小的方法可能有许多,在此我们设计两种不同的离散单元分裂算法. 如图1所示,每一个(αs,αr)采样点的离散单元由一个矩形表示,矩形面积大小为Δαs×Δαr,采样点位于长和宽的中间位置.θbound=θ0±Δθ/2为θ0分区边界.θmid为(αs,αr)采样点对应的θ值.当θbound穿过一个离散单元时,将该单元大小拆分为S1和S2两部分,并代替式(28)离散算法中的JsJrΔsΔr部分,分别累加到θ0及其附近的f(y,θ0)反演结果中.其中的S1和S2通过以下方式求解. 图1 矩形离散单元与散射角等值线分布 如果ds≥dr,S1有表达式: (31) 如果ds (32) 基于S1,S2有表达式: S2=dsdr-S1. (33) 以上即为离散单元矩形分裂法.主要依据平面几何方法分解矩形单元,形象且计算准确.但该方法也有缺点:(1)多次分支对比影响计算耗时;(2)在较高维度(四维空间)推广复杂.为此,我们设计了便于使用和推广的第二种分裂法. 图2 平行四边形离散单元与散射角等值线分布 (34a) (34b) 此处同样满足S1+S2=dsdr.该方法也可以通过αs单独控制离散单元,调换公式中的所有dr和ds即可实现.该分裂方法计算简洁方便,且适用于未来高维离散计算. 我们利用三种模型数据来验证我们提出的AD-GRT在角度域模型反演、多参数提取、数据重建拟合的有效性.同时,我们也测试提出的离散单元分裂法的计算效果,子波反滤波对分辨率的影响,以及错误背景模型下的数据重建拟合. 三个模型均选择Ricker子波作为震源子波(Wang, 2015),子波主频率fM均设为15 Hz.第一个模型地震记录使用波动方程有限差分法合成,另外两个利用GRT正变换(式(11))合成,以便验证AD-GRT正反变换的准确性.角度域模型在角度方向的采样间隔均设置为Δθ=1.5°,在[0°, 180°]范围内共取120个采样.负角度范围在本文临时不做分析. 水平单界面模型如图3a所示.水平界面在深度z=1000 m,并且界面上下声波波速分别为2000 m·s-1和2100 m·s-1,依照Gardner关系式ρ=0.31×c0.25(波速单位: m·s-1, 密度单位: g·cm-3)设定模型密度.模型在水平和垂直方向的网格间隔均为5 m.炮点和检波点均分布于边界线z=0 m上,且炮点间隔和检波点间隔均为10 m,从炮点到检波点的最大偏移距为2000 m.该模型地震记录使用声波波动方程有限差分方法合成,以验证准确波场数据反演结果的有效性.用于AD-GRT的背景波速和密度模型通过平滑原始模型来获得.图3b显示了震源x=2000 m的单炮记录,这里只显示了主要反射信息,排除了直达波信息. 图3 (a) 水平单界面模型; (b) 合成单炮地震记录 图4给出了利用AD-GRT反演方法(式(28))求解的角度域模型f(x,θ)反演结果(x=2000 m).为排除滤波导致的幅值震荡,此处设置震源子波为F(ω)=1,忽略子波反滤波操作.反演的主要信息分布在水平线z=1000 m附近,且同相轴具有明显的水平分布特征.同时,在反演结果边缘位置存在明显的倾斜噪声(见区域A),这与地震记录最大偏移距边界处的数据截断有关.记录边界具有数据不连续特征,而不连续性不符合提供的AD-GRT的局部近似假设(式(15)、(25)). 图4 角度域模型反演(忽略子波反滤波) 为了验证提供的离散单元分裂法在数值计算方面的有效性,我们分别利用传统离散方法、矩形分裂法和平行分裂法数值计算反演结果(如图4).三种反演结果在水平线z=1000 m上的幅值分布如图5所示.图5的横轴方向使用角度的余弦值表示,以显示角度域模型的线性倾斜分布特征(式(8)).其中的真实值是界面z=1000 m上下扰动值的差值(跳跃值),并且为方便对比,反演值乘了一个常数.由此可见,传统离散方法在角度域信息提取中易形成明显的锯齿状震荡,尤其在小角度范围内.这种震荡在地震记录稀疏观测情况下将会更为严重.相比之下,我们提出的两种离散单元分裂法均能提供非常连续平滑的幅值分布效果,并且反演幅值分布与模型真实值分布在有效角度范围内均能高度拟合.由此可证明AD-GRT反演结果是准确的,并且离散单元分裂法是有效的. 图5 角度域反演幅值分布 声波扰动参数f1和f2(式(8))可以通过数据拟合从角度域模型(图3)中提取.图6显示了双参数提取结果.图中f1提取结果非常靠近真实值(峰值相对误差0.46%,绝对误差0.00048).f2提取结果相对误差比较明显(峰值相对误差7.3%,绝对误差0.00078).这主要与两点有关:(1)f2绝对值远小于f1,在双参数共同提取过程中易形成相对误差,而f1和f2的绝对误差相差并不明显.(2)f2提取的是幅值分布的斜率或导数,f1主要与幅值平均分布有关(见式(8)),而幅值分布的斜率(导数)更容易受高频震荡噪声的干扰.因此,图6验证了基于角度域模型反演的多参数提取是合理的. 图6 角度域反演中的多参数提取结果 如图7所示,基于角度域模型反演结果(图4),地震数据可以利用GRT正变换(式(11))进行重建.图8显示了不同偏移距的地震道对比.由此可知,重建数据中的主要拟合误差是由数据截断导致的,该误差与图4区域A处的倾斜噪声相互对应.如果角度域中的倾斜噪声可以消除,则在重建数据中的拟合误差也可以压制.除了该部分拟合误差外,重建数据与原始数据可以高精度拟合.由此可见,我们提供的AD-GRT方法可在非迭代情况下实现高精度数据重建. 图7 利用角度域反演重建的地震数据 图8 重建地震数据道 该测试验证了我们提出的AD-GRT在角度域模型反演、多参数提取、数据重建的准确性,即使原始数据是由波动方程有限差分法合成.同时,该测试也证明了提供的离散单元分裂法在去除传统角度域离散方法存在的锯齿状震荡的有效性. 图9显示了水平层状模型的波速和密度模型.为验证AD-GRT正逆变换的准确性,由此以后的模型测试均使用GRT正变换(式(11))合成地震记录.图9a、b显示了波速和密度原始模型,背景模型通过平滑原始模型获得.图9c、d为扰动参数模型.由此可知,界面z=1000 m和z=1300 m分别为f1和f2单参数界面.模型网格间隔和震源接收点排布情况均与之前的水平单界面模型相同.图10显示了合成地震记录(震源x=2000 m). 图9 水平层状模型 图10 合成单炮地震记录 图11显示了角度域模型反演结果,其中(a)忽略了子波反滤波操作,而(b)执行了该操作.图11a中的红点是界面上下真实值的差值.对比图11a、b可知,子波反滤波明显提高了反演结果的分辨率,但也形成了一定程度的震荡,这对稳定性有一定影响.图11a、b中的反演值均能高精度的拟合真实值.另外,浅层反演结果形成了明显的倾斜噪声,这将影响之后的参数提取和数据重建. 图12显示了从角度域反演结果(图11)中提取的多参数(式(8)).图12a中的f2提取值误差比f1明显,图12b中的f2提取值震荡也较严重,这与之前的水平单界面模型情况相似.除了这些误差和震荡,图12a、b的参数提取值和真实值都能较好的拟合. 地震数据可以利用角度域模型反演结果(图11)进行重建(式(11)),如图13所示.图13a、b分别为忽略和使用子波反滤波情况下的重建数据,两种情况的重建拟合误差基本相同,这说明震源子波是否已知对AD-GRT的数据重建没有明显影响,这与AD-GRT正逆变换中存在震源子波F(ω)补偿有关.重建数据的主要误差为浅层强震动噪声,这与角度域反演结果(图11)中的浅层倾斜噪声直接相关.这是由于震源和接收点附近的波场不符合局部近似假设(式(15)、(25)),易形成畸形震动.除了浅层和边界的噪声以外,两种重建数据均能精确拟合原始地震数据.图14给出了忽略子波反滤波的不同偏移距的重建数据和原始数据对比,大部分位置重建和原始数据都能高精度拟合. 图11 角度域模型反演 图12 参数提取 图13 重建地震数据 图14 重建地震数据道 该模型测试验证了角度域模型与原始地震数据之间的对等关系,角度域模型保留了原始地震数据的绝大多数有效信息,并可支持稳定的多参数提取和精确的数据重建. 最后,我们提供复杂的Marmousi2模型测试,以验证AD-GRT在复杂模型中的有效性,讨论焦散区存在的问题,测试错误背景模型下的数据重建.图15a、b显示了波速和密度模型.地震记录使用GRT正变换(式(11))合成.震源和接收点分布在地表z=0 m,间隔均为10 m.最大偏移距为4000 m.图16显示了震源x=4000 m和x=8000 m的地震记录.可以看出,震源x=8000 m的地震记录分布明显复杂,这与震源附近区域模型结构复杂有关. 图15 Marmousi2模型 图16 合成地震记录 图17给出了位于x=6000 m和x=10000 m的角度域模型反演结果,该反演测试执行了子波反滤波以提高反演分辨率.由图可知,x=6000 m的角度域模型反演值能与真实值很好的拟合,而x=10000 m的反演值在许多位置不能匹配真实值.这与常规射线理论(ART)的应用有关.当前的AD-GRT利用ART获取波场传播信息,易在复杂结构区域形成焦散区,导致大量幅值和走时信息不连续.该不连续性不符合AD-GRT的局部近似假设(式(15)、(25)).在x=10000 m附近介质结构复杂,因此这里的反演结果误差明显. 图18显示了从角度域模型反演值(图17)中提取的多参数,图19为x=6000 m和x=10000 m的多参数提取值与真实值的对比.由图可知,提取的f1参数大部分都能非常靠近真实值,在复杂结构附近误差比较明显,这是角度域反演值(图17)误差导致的.而f2参数多数不能靠近真实值,该误差的形成原因与之前模型类似:(1) 一般f1参数值是f2的5倍以上,相对误差明显.(2)f2提取的是反演值对角度余弦的斜率(导数),易受局部震荡噪声的干扰.所以f2提取的稳定性较差.有关参数提取的优化技术有必要进行进一步研究. 图17 角度域模型反演(使用子波反滤波) 图18 参数提取值对比 图19 参数提取值对比 图20显示了利用角度域模型反演值重建的震源x=4000 m和x=8000 m的地震数据.由图20a、c可知,震源x=4000 m数据的主要噪声是由角度域反演值的浅层倾斜噪声导致的.另外,地震记录数据不连续也会造成重建误差.除此之外,震源x=4000 m的数据大部都能拟合原始地震数据.震源x=8000 m数据受复杂结构焦散区影响,波场传播幅值和走时不连续,导致大部分重建数据都有明显误差. 图20 重建地震数据 为了测试错误背景模型对角度域模型反演和数据重建的影响,同时分析波场传播信息的不连续性,我们利用错误背景模型进行角度域模型反演和数据重建.如图15c、d所示,错误背景模型是简单线性梯度模型.图21显示了错误背景模型下的角度域模型反演值.对比正确背景模型反演值(图17),x=6000 m的同相轴明显弯曲,而x=10000 m的角度域信息是混乱的.即使如此,该反演值也能保存大部分原始地震数据信息. 图22提供了利用错误角度域反演值(图21)重建的地震数据.有图22a、c可知,除了浅层的误差以外,大部分重建数据能够很好的拟合原始数据.图22b、d的重建数据误差也不明显,即使该震源数据是在复杂结构区域合成的.对比正确背景模型下的重建数据(图20),图22的重建数据反而能够更好的拟合原始数据.这是因为在错误的背景模型中不存在焦散区和传播信息不连续问题.图22浅层噪声的分布范围比图20偏大,这与背景模型近地表区域的波速较大有关.图23给出了使用正确和错误背景模型重建的数据对比(震源x=8000 m,偏移距1200 m).由图23可知,利用错误但简单的背景模型重建的数据比利用正确但复杂的背景模型重建的数据能更好的拟合原始数据. 图21 角度域模型反演(使用错误背景模型) 图22 重建地震数据(利用错误背景模型) 图23 重建地震数据对比(震源x=8000 m, 偏移距1200 m) Marmousi2模型测试说明了重建地震数据的精确度主要与波场传播信息的连续性有关,而背景模型是否正确对数据重建并不重要.这也很好的验证了角度域模型能保留绝大部分原始地震信息,不管该角度域模型反演值是否正确. 三个数值模型验证了新提出的AD-GRT反演方法的有效性.角度域模型的反演结果与真实值能够高精度拟合,双扰动参数可获得有效稳定的提取,重建地震数据能与原始数据很好的拟合. AD-GRT不要求背景模型是准确的.当背景模型是错误的,角度域模型反演结果也是错误的,多参数不能有效提取.但是,该角度域模型依旧很好的保存了原始地震数据的信息,能够非常精确的重建地震数据.并且,尽管该角度域模型反演结果是错误的,其包含的角度域信息可直接用于进一步改进背景速度模型. AD-GRT引入了子波反滤波(式(27)).如果地震数据的震源子波已知,子波反滤波操作能够明显提高角度域模型反演和多参数提取的分辨率和精度.但是子波反滤波对地震数据重建没有明显影响.如果子波未知,使用脉冲函数代替子波,地震数据仍然能够精确重建.这与式(7)、(26)中子波的正反滤波有关. 另外,AD-GRT当前的主要弊端在于传统射线理论(ART)的使用.ART的高频近似和介质平滑假设不符合复杂结构模型特征.AD-GRT的许多反演噪声与ART在焦散区生成的非连续波场传播信息有关,该非连续性不符合AD-GRT中的走时和幅值局部近似(式(15)、(25)).因此,有必要讨论频率相关的波场传播问题,为AD-GRT反演方法提供高精度的波场传播信息.当前,频率相关的射线理论已获得一定程度的发展(朱天飞, 2007; Protasov and Gadylshin, 2017).我们希望在此基础上进一步发展适用于AD-GRT的波场传播方法. 本文发展了一种新型的广义Radon变换(GRT)反演方法(2D声波介质),即角度域GRT(AD-GRT).利用局部走时和幅值近似搭建的AD-GRT实现了原始地震数据与角度域模型之间的准确转换.角度域模型能够记录大部分地震数据信息,支持精确的地震数据重建,即使背景模型不准确.并且,该角度域模型支持与角度相关的多扰动参数的准确稳定提取.同时,本文提出的两种角度域离散方法有效解决了传统角度域离散方法存在的幅值震荡问题.震源子波反滤波的引入明显提高了AD-GRT的反演分辨率.另外,AD-GRT保持了常规GRT方法的非迭代高效运行特征,角度域的添加对AD-GRT的计算耗时影响微弱,这与现有的地下偏移距扩展域反演方法相比具有明显优势.因此,新提出的AD-GRT有效解决了现有线性反演存在的计算成本过高、背景模型依赖、多参数提取不确定性等问题.在此基础上,我们下一步将扩展AD-GRT反演方法到2D弹性各向同性介质,进一步靠近实际地下介质模型.


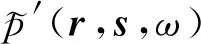

3 角度域离散方法

3.1 矩形分裂法

3.2 平行分裂法



4 数值试验
4.1 水平单界面模型





4.2 水平层状模型



4.3 Marmousi2模型







5 讨论
6 结论
