时间-空间高阶精度矩形交错网格隐式有限差分声波正演模拟

王静， 刘洋,3*， 周泓宇

1 中国石油大学(北京)油气资源与探测国家重点实验室， 北京 102249 2 中国石油大学(北京)CNPC物探重点实验室， 北京 102249 3 中国石油大学(北京)克拉玛依校区， 克拉玛依 834000

0 引言

有限差分方法(Kindelan et al.，1990；Robertsson et al.，1994；刘洋等，1998；Carcione et al.，2002；Moczo et al.，2002，2014；Du et al.，2009；Di Bartolo et al.，2012；Song et al.，2013；Fang et al.，2014；Etemadsaeed et al.，2016；Koene et al，2020；胡自多等，2021；赵明哲等，2022)因其简单易行、计算效率高和内存小的特点而被广泛应用于地震波正演、成像及反演中.有限差分方法的本质是采用多个临近点的加权求和来近似中心点的时间和空间导数.通常情况下，用离散差分算子数值逼近波动方程中的连续微分算子会引起时间及空间频散.两个重要因素将会影响数值频散的大小：差分格式和差分系数的求取方法，前者决定了用于近似中心差分点的时间及空间导数的网格点分布情况；后者给出了不同网格点的权重.规则网格(Dablain，1986)和交错网格(Yee，1966；Virieux，1984，1986；Graves，1996；董良国等，2000；Moczo et al.，2000；裴正林，2004；李振春等，2007；Dong et al.，2013；姜占东等，2021)是有限差分方法中最常用的两种用于求解一阶偏导数的差分格式.与规则网格相比，交错网格因其具有更高的精度和更好的稳定性而被广泛应用于地震波正演模拟中.

有限差分模拟的空间精度可以通过增加差分算子长度来提高，如高阶显式和隐式(Lele，1992；Du et al.，2009；Liu and Sen，2009a；Chu and Stoffa，2012a，c；Liu，2014；陈东等，2016；Yang et al.，2017；Wang and Liu，2018；Wang et al.，2018，2021)交错网格有限差分方法，前者通过增加空间算子长度很容易实现空间高阶精度模拟，但存在“饱和效应”(Kosloff et al.，2010)的问题，即空间精度的提高率随着算子长度的增加而降低，并且增加了大量的计算消耗.隐式有限差分方法的发展很好地解决了这一问题，隐式差分方法可以使用较短的算子长度达到与显式方法相同的精度，且有效降低了计算耗时.然而上述显式和隐式有限差分方法的时间导数通常由二阶中心差分格式进行离散，导致在长时间的波场传播过程中，时间频散变得严重，特别是当使用大的时间步长时.因此，更多学者致力于发展时间高精度波场模拟方法(Lax and Wendroff，1964；Dablain，1986；Tam and Webb，1993；Etgen and Brandsberg-Dahl，2009；Fowler et al.，2010；Alkhalifah，2013；梁文全等，2013；Tan and Huang，2014；Ren et al.，2017；Koene et al.，2018；Ren and Li，2019；Zhou et al.，2021).

有限差分模拟的时间精度可以通过采用空间导数代替时间导数的Lax-Wendroff方法(Lax and Wendroff，1964)来实现，然而精确的时间高阶算法依赖于使用谱方法计算空间导数，因此计算量大.发展时间高阶有限差分方法能够有效提高计算效率.Finkelstein和Kastner(2007，2008)给出了在固定频率下满足时空域频散关系的有限差分系数，实现了对特定频率下时间频散的有效压制.Liu和Sen(2009b，2011)进一步发展了连续频率范围内时空域规则网格和交错网格有限差分系数的求取方法，相比于传统空间域方法的时间二阶精度，该方法在二维情况下可将8个波传播方向上的时间精度提高到任意偶数阶.为了进一步提高模拟精度，Liu和Sen(2013)提出了菱形差分格式，该方法在任意方向上均可达到时间及空间高阶精度，但相比于传统十字形差分格式，增加了一定的计算成本.Tan和Huang(2014)之后发展了时间4阶和6阶精度、空间均为任意偶数阶精度的两种时空域交错网格有限差分格式，Chen等(2016)将其推广为更加适用于某些特殊地质情况的矩形网格离散形式的差分方法.Ren等(2017)采用十字形和菱形结合的差分格式(Wang et al.，2016)实现了交错网格时间高阶有限差分声波正演模拟，紧接着类似的工作被拓展到弹性波模拟(Ren and Li，2017).

差分系数的求取方法也直接影响数值模拟结果，泰勒级数展开方法可以在低波数区域达到较高的模拟精度，但随着波数的增加，精度会迅速下降.为了在更大的波数范围获得高精度模拟结果，许多学者对空间差分算子优化和时空差分算子同时优化策略进行了研究.Chu和Stoffa(2012b)发现，通过在波数域设置一些二项式窗口推导出的优化差分系数可以有效压制数值频散.Zhang和Yao(2013)利用模拟退火算法求解由最大范数构造的目标函数，有效提高了模拟精度和效率.Liu(2014)发展了全局优化的显式和隐式交错网格有限差分方法用于计算波动方程的一阶偏导数，该方法通过最小化选定区间内的误差来获得优化的空间差分系数.对于多孔弹性介质，Itzá等(2016)基于全局最优策略的隐式交错网格差分格式实现了二维低频介质中传播的地震波模拟.Ren和Li(2019)提出了基于最小二乘优化算法的时间高阶空间隐式有限差分方法，但该方法没有依据整个离散波动方程的频散关系来近似时间和空间导数，并不是真正意义上的时空域方法.因此，时空域时间高阶空间隐式交错网格有限差分方法还具有很大的研究潜力以提高地震波正演模拟精度.

现阶段发展的时间高阶有限差分方法主要为空间显式或隐式方法，但通常为基于正方形网格离散形式的，将低了其对实际地质问题的灵活适应性.本文发展了一种基于矩形网格离散形式的时间高阶空间隐式有限差分格式用于精确且高效地数值求解一阶变密度声波方程，该差分格式在传统十字形矩形交错网格隐式差分格式的基础上增加了一些额外的离散点，达到有效压制时间频散的目的.基于本文新差分格式的时空域频散关系及变量替换的思想，我们分别采用泰勒级数展开和最小二乘优化两种方法来计算相应的有限差分系数.通过频散和稳定性分析、数值算例来验证本文基于泰勒级数展开和最小二乘优化的新差分方法相较于传统时间二阶空间域隐式差分方法在模拟精度、稳定性和效率方面的优势.

1 矩形交错网格隐式有限差分格式

二维介质中，一阶应力-速度变密度声波方程可表述为：

(1)

其中，p(x,z,t)为标量压力场，vx(x,z,t)和vz(x,z,t)分别代表x和z方向的质点偏振速度.K(x,z)=ρ(x,z)c2(x,z)为体积模量，ρ(x,z)和c(x,z)分别为介质密度和地震波传播速度.

1.1 传统时间二阶隐式有限差分格式

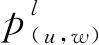
(2a)

(2b)

(2c)

其中：

(3a)

(3b)

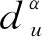
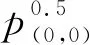
(4a)

(4b)

(4c)

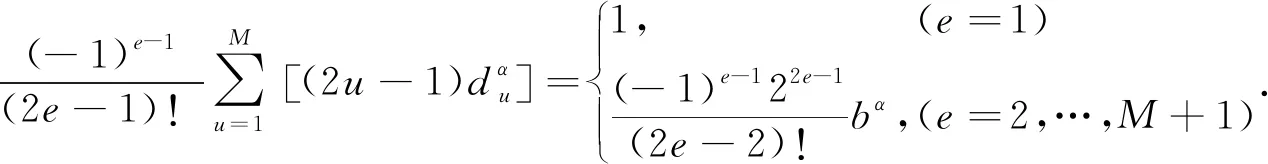
(5)

据Liu和Sen(2009a)的分析可知，上述基于泰勒级数展开的空间域隐式差分格式可以达到2M+2阶空间精度，具有与传统4M阶显式方法(当bα=0时)基本相同的精度.相较于显式有限差分方法，隐式方法虽然能够显著提高空间模拟精度，但时间精度依旧只能够达到二阶.为方便叙述，我们将基于泰勒级数展开求取差分系数的空间任意偶数阶、时间二阶精度的矩形交错网格隐式有限差分方法计为泰勒(2M+2，2).

1.2 新时间高阶空间隐式有限差分格式

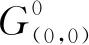
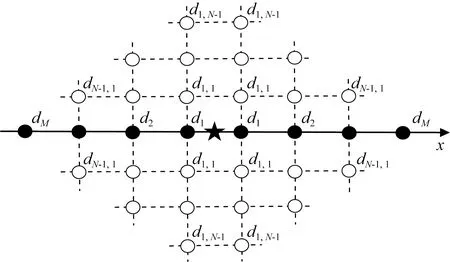
图1 本文基于矩形交错网格离散形式的时间高阶空间隐式有限差分格式离散∂/∂x示意图

(6a)

(6b)

(7a)

(7b)

(7c)

该差分格式具有时间2N阶精度和空间2M+2阶精度，适用于任意矩形网格剖分的一阶波动方程的时空域隐式有限差分方法.

2 新时间高阶空间隐式有限差分格式时空域差分系数求取方法

基于平面波理论和变量替换的思想，本文分别采用泰勒级数展开和线性优化两种方法求取相应的差分系数并给出时间及空间精度具体阶数的推导证明.为方便叙述，将本文具有空间2M+2阶和时间2N阶精度的矩形交错网格时间高阶空间隐式有限差分格式记为(2M+2，2N)，则基于该格式的采用泰勒级数展开和线性优化方法求取差分系数的两种有限差分方法可分别记为泰勒(2M+2，2N)和优化(2M+2，2N).

2.1 泰勒级数展开方法

假设本文(2M+2，2N)差分格式(7)具有如下形式的平面波解：

(8a)

(8b)

(8c)

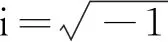
(9)

其中：

(10a)

(10b)

(11a)

(11b)

以及rx=cτ/hx、rz=cτ/hz分别为x、z方向的网格比.

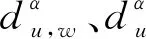
(12)

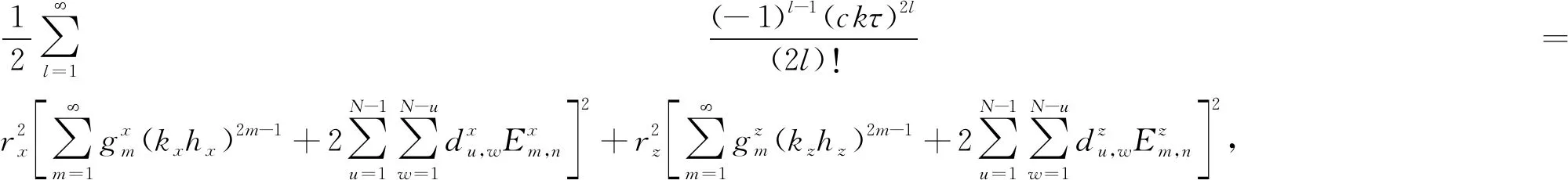
(13)

其中：

(14a)

(14b)

(15)

并将独立波数项(kαhα)2l(α=x或z)和混合波数项(kxhx)2l-2ξ(kzhz)2ξ前面的系数进行整合可以得到：

(16)

其中：

(17a)

(17b)

(18a)

(18b)

通过分别对比公式(16)等号两端的独立波数项(kαhα)2l和混合波数项(kxhx)2l-2ξ(kzhz)2ξ前面的系数，可以得到如下表达式：

(19)

(20)

(21)

将其进一步整理为：

(22)

(23)

2.2 线性优化方法

分解出公式(9)中的仅包含独立波数项kα的表达式并对等号左侧余弦函数应用二倍角公式可得：

×sin[(u-0.5)β]，

(24)

(25)

其中：

(26)

(27)

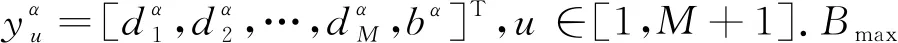
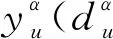
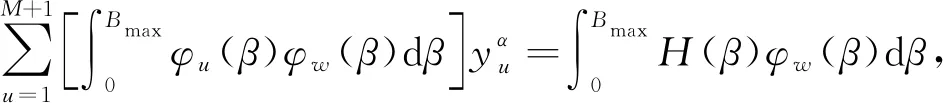
(w=1,2,…,M+1).

(28)

为了获得求解公式(28)所需的Bmax，我们定义优化差分系数求取过程的最大误差限定条件为：

(29)

其中：

(30)

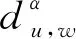
3 频散分析

本节通过对比分析本文泰勒(2M+2，2N)和优化(2M+2，2N)有限差分方法与传统泰勒(2M+2，2)有限差分方法的频散曲线来表明本文两种差分方法在模拟精度方面的优势.

数值模拟速度与真实速度的比值δ可以衡量不同有限差分方法的数值频散，基于公式(9)，可推导出本文(2M+2，2N)差分格式的频散关系为：

(31)

其中，cFD和c分别为数值模拟速度和真实速度.δ>1，表现为时间频散；δ<1，表现为空间频散；δ=1，则无数值频散.

图2展示了本文泰勒(2M+2，2N)和优化(2M+2，2N)有限差分方法的频散曲线随着空间算子长度参数M和时间算子长度参数N的变化.x和z方向的网格比分别为rx=0.35、rz=0.42，设置优化(2M+2，2N)差分方法的差分系数求取时的最大允许误差为10-4，其他相关参数已在图中注明.由图2a(θ=0)可见：随着M的增大，本文两种差分方法的频散曲线均趋近于δ=1的零频散参考线；与泰勒(2M+2，2N)差分方法相比，优化(2M+2，2N)差分方法能够在更大的波数区间内压制空间频散，即取得更高的空间模拟精度.由图2b(θ=π/4)可见：在给定相同M的情况下，随着N的增大，本文两种差分方法的频散曲线形态相近(相同颜色的频散曲线基本重合)，同时时间频散都得到了很好的压制.因此，本文(2M+2，2N)差分格式的空间和时间模拟精度的提高可以通过采用更大的M和N来实现.

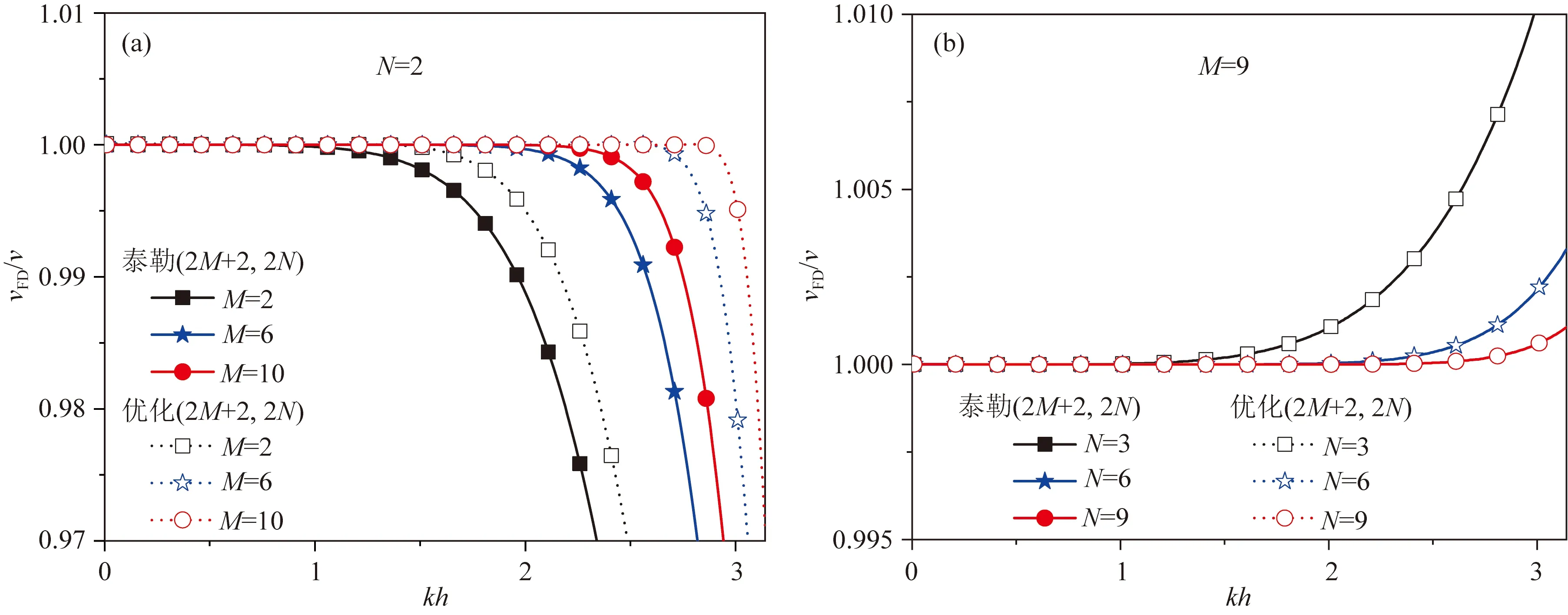
图2 本文两种矩形交错网格时间高阶空间隐式有限差分方法的频散曲线随M和N的变化

图3给出了本文泰勒(2M+2，2N)和优化(2M+2，2N)差分方法与传统泰勒(2M+2，2)差分方法在三种时间步长的情况下沿不同传播方向(0-π/4)的频散曲线.设置空间算子长度参数M= 6，速度c= 2200 m·s-1，x、z方向网格离散间距分别为22 m、18 m，其余参数可见图上注释.如图3a—c所示：当采用较小的时间步长τ=1 ms(网格比rx=1、rz=1.23)时，三种矩形交错网格隐式有限差分方法的频散曲线差异不大，均能获得较为满意的模拟结果.当时间步长τ增大到2 ms(网格比rx=2、rz=2.44)甚至3 ms(网格比rx=3、rz=3.67)时，传统泰勒(2M+2，2)差分方法的频散曲线逐渐向上远离δ=1的零频散参考线，出现了严重的时间频散(图3d、g).然而，通过增大时间算子长度参数N，本文的泰勒(2M+2，2N)和优化(2M+2，2N)有限差分方法均未表现出明显的时间频散，并且优化(2M+2，2N)差分方法在更大的波数区间内进一步压制了空间频散，是三种矩形交错网格隐式有限差分方法中模拟精度最高的.通过以上对比分析可以发现，当使用大时间步长进行波场模拟时，传统泰勒(2M+2，2)差分方法的时间频散会显著增加，模拟精度较低，而本文两种基于(2M+2，2N)差分格式的时间高阶空间隐式有限差分方法可通过增加时间算子长度参数N来有效压制时间频散，因此并不会导致模拟精度的降低，并且优化(2M+2，2N)差分方法又能在此基础上进一步提高空间模拟精度.本文两种矩形交错网格时间高阶空间隐式有限差分方法更适用于求解大时间步长延拓时的地震波场，在获得高精度模拟结果的同时能有效地节省计算时间.

图3 三种矩形交错网格隐式有限差分方法的频散曲线随时间步长τ的变化

4 稳定性分析

本节采用传统的特征值方法来推导本文(2M+2，2N)差分格式的稳定性条件.对公式(9)进行空间傅里叶变换，可得到以下表达式：

(32)

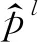
(33)

考虑到频散误差会随波数增加而增加，因此将最大Nyquist波数kxhx=kzhz=π代入公式(33)中并进行整理可得：

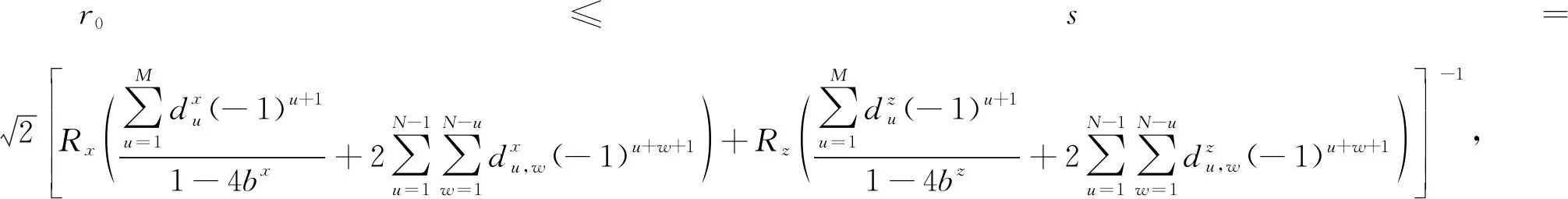
(34)

图4展示了本文泰勒(2M+2，2N)和优化(2M+2，2N)两种矩形交错网格时间高阶空间隐式有限差分方法随空间和时间算子长度参数M和N的稳定性变化曲线，并与传统泰勒(2M+2，2)差分方法的稳定性结果进行对比.相关参数设置为：rx=0.39、rz=0.44，基于最小二乘优化方法求取差分系数时的最大允许误差为10-4.如图4所示：三种矩形交错网格隐式有限差分方法的稳定性均随着空间算子长度参数M的增加而降低，其中传统泰勒(2M+2，2)差分方法具有最严格的稳定性条件；本文泰勒(2M+2，2N)差分方法具有最宽松的稳定性条件.当时间算子长度参数N增加时，无论是泰勒(2M+2，2N)还是优化(2M+2，2N)差分方法的稳定性条件均得到明显改善，表明时间精度的提高可以有效增强地震波场模拟的稳定性.

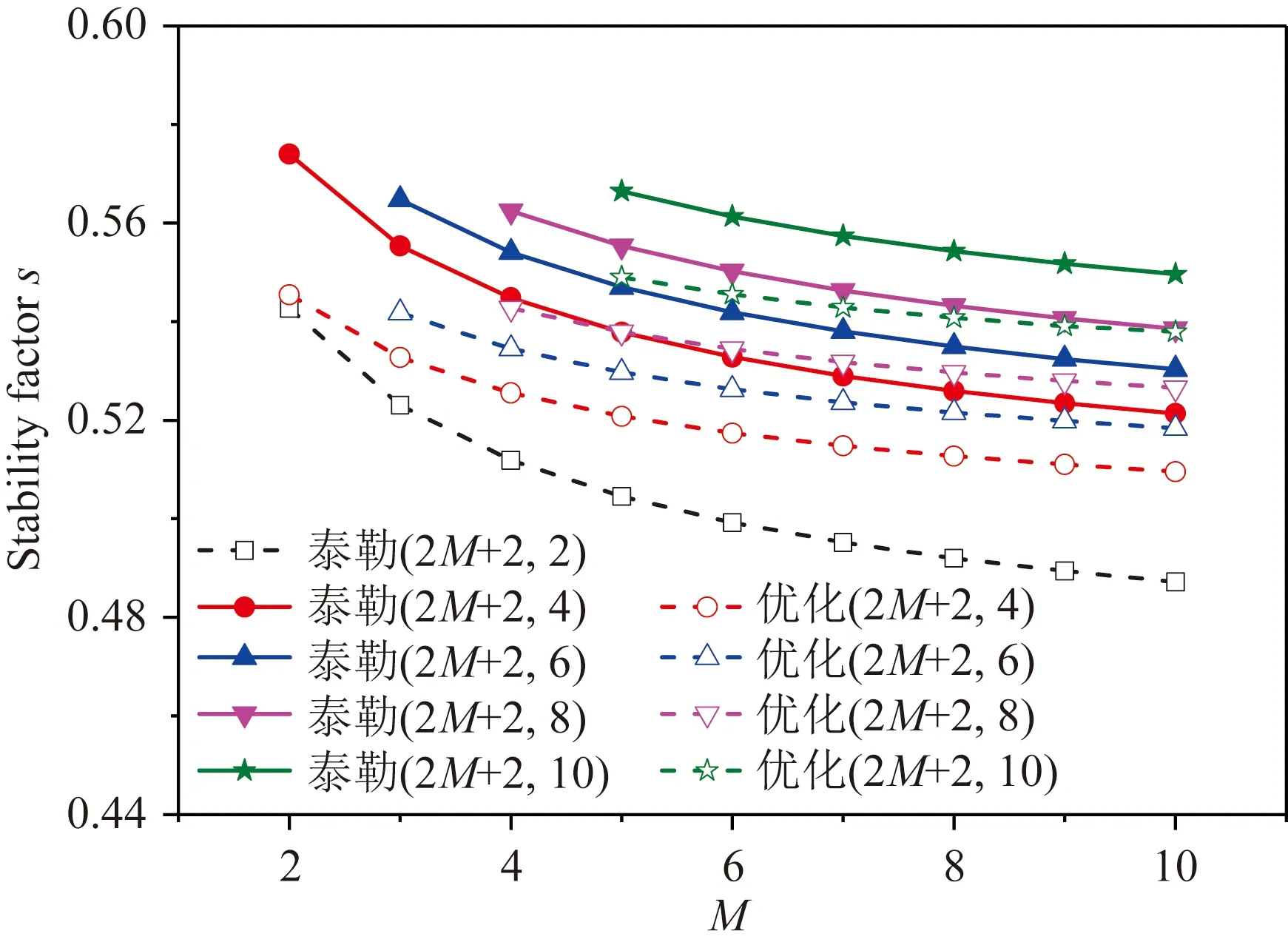
图4 三种矩形交错网格隐式有限差分方法的稳定性曲线

5 模型算例

本节将采用简单均匀介质模型和二维SEG/EAGE盐丘模型来验证本文两种矩形交错网格时间高阶空间隐式有限差分方法相较于传统空间域时间二阶空间高阶隐式差分方法具有更高的模拟精度和计算效率.

5.1 简单模型

第一个数值算例是模拟速度为2500 m·s-1的地震波在6 km × 6 km均匀介质模型中传播的地震响应.时间步长为2 ms，模型纵、横向的网格比分别0.33和0.25.三种矩形交错网格隐式有限差分方法的空间算子长度参数M为5，其中本文两种矩形交错网格时间高阶空间隐式有限差分方法的时间算子长度参数N为3.震源选择主频为20 Hz的雷克子波并在模型的中心点处激发.

图5给出了三种矩形交错网格隐式有限差分方法1.9 s时的波场快照，参考解(图5a)为传统泰勒(2M+2，2)差分方法取M=12，τ=0.5 ms时的模拟结果.为了更加精确地对比波场模拟结果，我们将每个波场快照中白色虚线长方形框内图像进行放大显示并置于相应波场图下方.如图5b所示：传统泰勒(2M+2，2)差分方法会产生明显的时间(白色箭头标识处)和空间(白色实线框标识处)频散，因横向空间采样间隔(20 m)大于纵向空间采样间隔(15 m)导致波场快照横向上的空间频散更加严重.本文泰勒(2M+2，2N)差分方法的波场快照中(图5c)虽然显示出与传统泰勒(2M+2，2)差分方法的波场快照中(图5b)相近的空间频散(白色实线框标识处)，然而并无可观察到的时间频散，表明本文泰勒(2M+2，2N)差分方法能够有效压制时间频散，提高时间模拟精度.图5c中可观察到的空间频散可采用最小二乘优化算法来进一步压制，获得如图5d所示的与参考解最为接近的波场快照结果.三种方法中，本文优化(2M+2，2N)差分方法能够有效减少时间和空间频散，获得最为精确的波场模拟结果.

图5 不同矩形交错网格隐式有限差分方法1.9 s时的波场快照及其局部放大图

5.2 二维SEG/EAGE盐丘模型

为了进一步验证本文两种矩形交错网格时间高阶空间隐式有限差分方法在模拟精度和效率方面的优势，下面对二维SEG/EAGE盐丘模型(图6)进行一阶变密度声波方程正演模拟.该模型的速度变化范围为1.5 km·s-1到4.5 km·s-1，密度由经验公式(Castagna et al., 1993)获得，计算区域大小为6 km×2 km且具有18 m×10 m的空间采样间隔，时间步长为1.5 ms.震源为27 Hz主频的雷克子波并在(x，z)=(6 km，0.1 km)的位置处激发.接收点均匀排布在地表，接收总时长为4 s.图7展示了采用三种矩形交错网格隐式有限差分方法对图6中SEG/EAGE盐丘模型进行正演模拟2.3 s时的波场快照和参考解(传统泰勒(2M+2，2)差分方法，M=15，τ=0.75 ms)，以及相应的局部放大图，图8为最终接收到地震记录的局部放大图.由图7和图8可见：

图6 二维SEG/EAGE盐丘速度(a)及密度(b)模型

(1)传统泰勒(2M+2，2)差分方法的正演模拟结果会产生明显的空间和时间频散，如图7b和图8b中白色实线框和白色箭头标识处所示.本文的泰勒(2M+2，2N)差分方法和优化(2M+2，2N)差分方法的波场快照(图7c、d)及地震记录(图8c、d)中基本观察不到时间频散，表明本文的两种时间高阶空间隐式有限差分方法能显著提高地震波场正演模拟的时间精度.

图7 SEG/EAGE盐丘模型中不同矩形交错网格隐式有限差分方法2.3 s时的波场快照

(2)本文泰勒(2M+2，2N)差分方法的波场模拟结果(图7c和图8c)在有效压制时间频散的同时仍残留一些空间频散，优化(2M+2，2N)差分方法则可以很好地解决这一问题，获得与参考解基本相近的时间和空间高精度正演模拟结果(图7d和图8d).

图8 SEG/EAGE盐丘模型中三种矩形交错网格隐式有限差分方法计算所得地震记录

接下来，仍然采用二维SEG/EAGE盐丘模型来说明本文两种矩形交错网格时间高阶空间隐式有限差分方法的效率优势.为了保证对比的公平性，我们基于统一计算平台(i7-4790内核，3.60 GHz处理器，8 GB内存)，并保证三种差分方法之间具有相同精度的前提下比较计算耗时.定义数值模拟解与参考解之间的归一化L2范数误差(Bohlen and Saenger，2006)来定量衡量每种差分方法的模拟精度：

(35)

其中，Iσ和Jσ分别代表数值模拟结果和参考解，L是空间采样总点数.

图9为三种矩形交错网格隐式有限差分方法在(3450 m, 500 m)处的波形图.由图可知：当时间步长为1 ms时，传统泰勒(2M+2，2)差分方法计算出的波形与参考解差异较大，表现出明显的相位偏移(时间频散)，由公式(35)计算所得误差为0.236.然而本文两种矩形交错网格时间高阶空间隐式有限差分方法在相同时间步长的情况下模拟出的波形与参考解基本匹配，其中泰勒(2M+2，2N)差分方法的误差为0.081；优化(2M+2，2N)差分方法能进一步提高模拟精度，其与参考解的误差仅为0.013.为了使传统泰勒(2M+2，2)差分方法能够达到与本文泰勒(2M+2，2N)和优化(2M+2，2N)差分方法基本相同的精度，我们缩短用于传统泰勒(2M+2，2)差分方法正演模拟的时间步长至原来的一半(τ=0.5 ms).据此，传统泰勒(2M+2，2)差分方法与参考解匹配良好，误差降为0.089.由此可知：本文两种(2M+2，2N)差分方法即便采用了相较于传统泰勒(2M+2，2)差分方法两倍的时间步长，其模拟精度仍然高于传统泰勒(2M+2，2)方法.在保证三种矩形交错网格隐式有限差分方法基本达到了相同精度的前提下，表1列出了SEG/EAGE盐丘模型(图6)中三种差分方法正演模拟所需的计算时间.本文泰勒(2M+2，2N)和优化(2M+2，2N)差分方法的计算耗时分别为662.57 s和653.26 s，相较于传统泰勒(2M+2，2)差分方法879.91 s的计算时间，分别节省了24.7%和25.8%.值得注意的是，尽管传统泰勒(2M+2，2)差分方法以增加计算成本为代价(时间步长减半)，其模拟精度仍然低于本文两种(2M+2，2N)差分方法.因此，本文(2M+2，2N)有限差分格式在保证高精度正演模拟的同时可以采用更大的时间步长，从而提高计算效率.

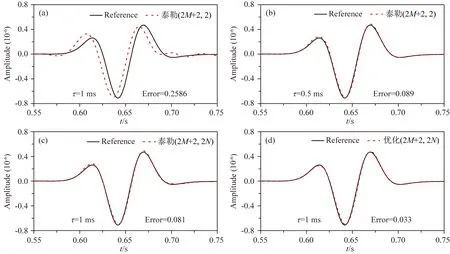
图9 SEG/EAGE盐丘模型中三种矩形交错网格隐式有限差分方法计算所得波形图

表1 SEG/EAGE盐丘模型中三种矩形交错网格隐式有限差分方法地震波正演模拟计算时间(CPU)

6 结论

本文发展的适用于矩形网格剖分形式的时间高阶空间隐式有限差分格式可以显著提高一阶变密度声波方程的模拟精度.基于变量替换的思想，使得本文时间高阶空间隐式有限差分格式的时空域频散关系与差分系数之间的非线性关系线性化，从而降低了差分系数的求解难度.相应的有限差分系数的求取采用了泰勒级数展开和线性优化两种方法，前者可以达到时间2N阶、空间2M+2阶模拟精度，后者通过基于泰勒级数展开和最小二乘结合的线性优化方法，进一步提高了本文矩形交错网格时间高阶空间隐式有限差分格式的空间模拟精度.通过与传统空间域矩形交错网格隐式有限差分格式的多方面对比，表明了本文差分格式在模拟精度和稳定性方面的优越性.此外，在相同精度的情况下，基于本文差分格式的泰勒(2M+2，2N)和优化(2M+2，2N)差分方法可以使用比传统(2M+2，2)差分方法更大的时间步长，因此降低了计算耗时，更适用于大尺度模型的地震波场模拟.