初中生“数学抽象”素养培养的实践与思考

山东省淄博市高新技术产业开发区第一中学 刘 淼

数学学科核心素养是通过数学学习形成的、具有数学学科特性的必备品格和关键能力。其中，数学抽象素养是数学核心素养的“灵魂”，是数学教学的核心。下面笔者以4个教学片断为例，说明初中数学教学中数学抽象素养的培养策略。

一、以数学核心概念形成根基

概念是思维的单元和细胞，重视概念教学，提升概念教学水平，其中最切实的是抓住数学核心概念形成的教学。选取学生熟悉的典型实例，提供丰富材料，让学生形成完整的数学抽象过程，在概念形成的教学中学会数学抽象。

案例1 函数的概念课

（一）创设情境，初步形成概念

情境1：在旅途中偶遇某水库，水库的某处水深h（米）与蓄水量V（万立方米），数据变化见表1。

表1

（1）在这个变化过程中，有几个变量？

（2）这两个量的数值是否发生变化？V的值随h的值的变化而变化吗？

（3）当水深h确定时，该水库蓄水量V是否确定？唯一吗？举例说明。

（二）归纳本质，形成概念

本案例从“问题情境—抽象概括—解释应用”的线索展开，通过一组类似问题的追问，将学生对函数概念的理解由“变化而变化”递进至“确定而确定”，顺势归纳出概念。此后通过正反例的辨析从多角度理解概念。由此可见，本案例着力让学生充分经历函数概念的发生发展过程，使得学生逐渐将抽象的函数概念具体化、清晰化，由此顺利达成学习目标。

二、以数学抽象概括能力形成为重点

培养数学抽象素养，在数学教学中适时进行由特殊到一般——数学模型化思维是一个有效的策略。由特殊到一般的数学抽象概括就是将“数学材料数学化，发现不同对象的共同特征”。这种抽象概括能力可以在知识的发生、发展过程的探究中形成。

案例2 探索勾股定理

问题1：在纸上作出若干个直角三角形，分别测量它们的三条边，观察三边的平方之间有怎样的关系？

问题2：如图1①直角三角形三边的平方分别是多少，它们满足上面所猜想的关系吗？你是如何计算的？图1②呢？

问题3：对图1③中的三角形是否还满足这样的关系？你又是如何计算的？

问题4：如果直角三角形的两直角边分别为a，b，c，上面所猜想的数量关系还成立吗？你能利用图1④说明其正确性吗？

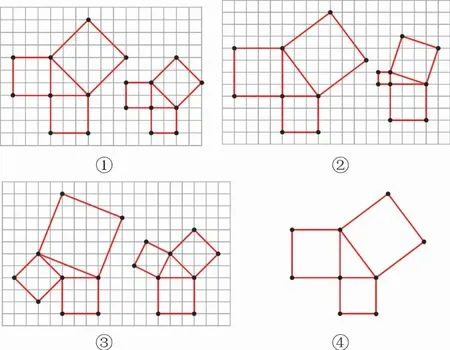
图1

本探究过程力图让学生通过对大量直角三角形的测量活动（问题1），归纳出a，b，c之间的关系式：a2+b2＝c2。基于测量的误差学生可能还难以确认所猜想得到的平方关系，必然产生进一步验证的必要性。因此借助网格纸通过“割补法”验证了特殊的等腰直角三角形推广到一般直角三角形时，结论的正确性（问题2），同时验证了该关系式的适用范围——直角三角形（问题3）。至此学生利用合情推理得出了相关结论。合情推理得到的结论必须通过演绎推理证明其正确性。当直角三角形两直角边的长度不再是整数时，跳出格点看图，让学生感受到勾股定理的一般性（问题4）。

教师在上述探究活动中注重培养学生由特殊到一般的数学抽象素养（从等腰三角形，到直角边长为整数的直角三角形，到直角边长为小数的直角三角形，进而到直角边长为a，b，c的直角三角形）。让学生在活动中不断提升概括能力。

三、以数学知识的温故知新为途径

数学具有逐级抽象的特点，较高一级的抽象要依赖于较低一级的抽象。数学的这种逐级抽象性反映着数学的系统性。这种数学逐级抽象性的特点体现到数学学习过程中，就要重视数学知识的“温故知新”。

案例3 二元一次方程组的解法

二元一次方程组的解法既是“通法”又是“未知化已知”的典型课例。教材从一道应用题出发，通过设元，列出方程组

由①得y＝x-2，然后由于方程组中相同的字母代表同一对象，所以方程②中的y也等于x-2，可以用x-2代替方程②中的y，得到一元一次方程，再引领学生解一元一次方程组。显然上述解读型的示范性教学没有为新知的抽象创造必要的条件，不能较好地凸显转化思想的重要性，不利于学生体悟二元一次方程组的解法——代入消元法的真谛。因此在学习新知时，必要及时复习旧知，这即符合数学的发展规律，又符合学生认知的发展规律，既能加深对新知识的理解，又能从中领悟到数学抽象的层次性，不断提高数学抽象能力。

四、以数学实验活动为驱动

从数学的发展看，它本身也是充满着观察与猜想的探索活动。教师应充分挖掘向学生展现“做数学”的过程。通过引导学生观察、动手操作、比较分析、猜想归纳，在“做数学”中学数学，获得数学学习的体验，并从中提升数学抽象能力。

案例4 三角形内角和定理

课前准备三角形纸片。

问题1：在小学我们已经知道任意一个三角形内角和等于180°。还记得当时我们是如何发现和验证这一结论的？请利用手中的三角形纸片进行探究。

问题2：从拼图上看，3个角组成了平角，就能说明3个内角的和一定是180°吗？

问题3：我们撕下其中的两个角移动到与第三个角凑成平角的位置，利用平角的定义，得出三角形内角和180°的结论。如果不撕下两个角，你能通过作图的方法达到移动这两个角的效果吗？（或者：如果不移动这两个角，能否做出某些辅助的先，实现这种移动呢？）

问题4：若果只能撕下一个角，是否也能得到上面的结论？

问题5：根据学习过的基本事实和定理，你能用自己的语言说所这一结论的证明思路吗？请尝试用简洁的语言写出这一证明过程？

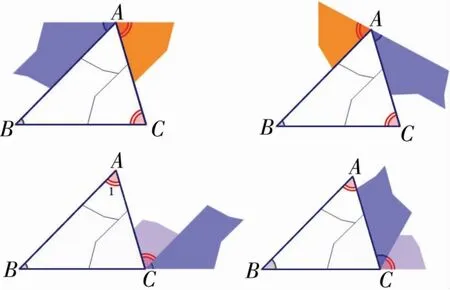
图2 展示拼图

本案例中五个问题以“为什么内角和180°→如何实现移动角的效果→如何进行证明”为主线步步深入，紧紧围绕性质的发生、发展、形成进行设计。通过拼图活动，启发学生对直观模型进行抽象提炼，对移纸片进行严格的数学描述，得到三角形内角和定理。搭建适切的、脚手架式的五个问题串，一步一步、环环相扣、由浅入深，在“最近发展区”让学生处于“跳一跳”摘到“桃子”的状态，促进学生在“做数学”中提升抽象思维能力。