具抗原性和简化Holling-IV型发生率肿瘤与免疫系统的定性分析
2023-01-10贺芳芳朱惠延林晋章
贺芳芳,朱惠延,林晋章
(南华大学 数理学院,湖南 衡阳421001)
0 引 言
肿瘤是指细胞在某些因素的作用下,其基因发生改变,从而发生异常增殖。免疫系统是人体抵御外来病原菌侵犯的系统之一,其具有免疫监视、防御和调控的作用。研究发现,肿瘤细胞的表面抗原可能与正常细胞的相同,也可能不同,因此会发生免疫应答[1]。另一方面,免疫系统是由免疫器官、免疫细胞以及免疫活性物质组成的一个非常复杂的网络,免疫系统可以促进和抑制肿瘤细胞的发展。目前,肿瘤和免疫系统之间的作用机理仍是在癌症和免疫学中最具有挑战的问题之一[2]。
为了更好地理解这一复杂的生物变化过程,国内外许多专家利用数学建模方法积极开展研究。早在1994年,V.A.Kuznetsov等提出肿瘤与免疫系统之间相互竞争的数学模型[3]
(1)

在模型(1)的基础上,许多数学模型被相继提出,有二维模型、三维模型、加入随机项模型、加入时滞项模型、加入治疗项模型等等,许多专家学者研究这些模型的动力学性质[4-10]。1998年,D.Kirschner和J.C.Panetta在三维模型中用cT描述抗原性[6]。谢鑫等在M.Galach提出的二维模型中加入抗原项cT[8-9],得到模型
(2)
并对系统(2)进行了动力学性态研究。
考虑到采用简化Holling-IV型发生率能更好地反映生物现象[11],本文在系统(2)的基础上,研究具简化Holling-IV型发生率的模型,
(3)
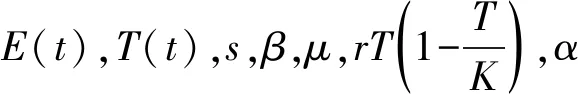
1 模型化简
(4)
(5)
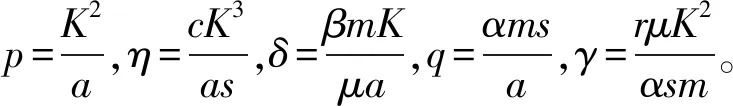
2 平衡点的存在性
(6)
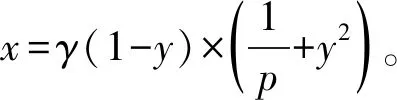

(7)
方程(7)等价于[12]
y3+ay2+by+c=0。
(8)
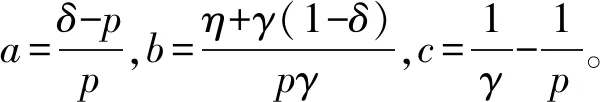
z3+l1z+l2=0。
(9)


定理1 条件(H1)成立,当l1=0且l2<0,或l1<0且l2=0,或Δ>0且l2<0,或Δ=0且l2<0,或Δ<0且l2<0时,系统(5)有且仅有一个有瘤平衡点;当Δ=0且l2>0时,系统(5)存在两个相等的有瘤平衡点;当Δ<0且l2>0时,系统(5)存在两个不同的有瘤平衡点。
3 局部稳定性
在二维平面系统中,局部渐进稳定的平衡点有两种类型,焦点和结点。类型不同,系统的轨线收敛于平衡点的方式不同,本节首先分别讨论无瘤平衡点P0(1,0)和有瘤平衡点P(x*,y*)的稳定性,最后分析稳定平衡点的类型。
3.1 无瘤平衡点的稳定性
首先求得系统(5)在无瘤平衡点P0(1,0)的Jacobi矩阵
(10)
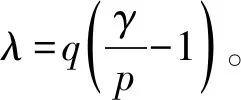
接着分析当γ=p时系统(5)在瘤平衡点P0附近的动力学性质。
令u=x-1,v=y并代入系统(5)中,得
(11)
接着在无瘤平衡点P0(1,0)处对系统(11)作线性化处理,得
其系数矩阵对应的特征值为λ1=-1和λ2=0,然后对系统(11)作非退化的线性变换,令
系统(11)则变为
(12)
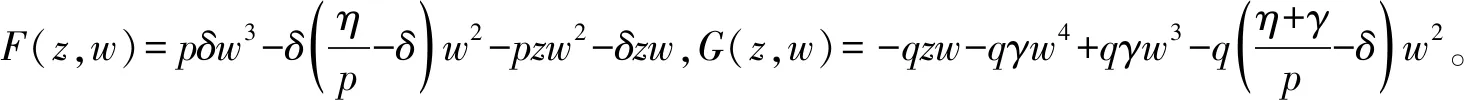
易知系统(12)满足局部中心流行存在性的条件,故局部中心流形h(w)存在,设为
z=h(w)=aw2+bw3+o(w3)
利用中心流行的不变性,解得
故系统(12)在原点的中心流行为
(13)
将式(13)代入系统(12)的第二式中,得
(14)
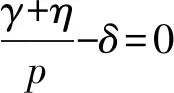
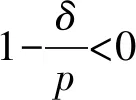
(15)
其中:
再次运用中心流行定理,故系统(15)在原点的中心流行为
并代入系统(15)的第二式中,得
(16)
由式(16)知,无瘤平衡点P0(1,0)是不稳定的。这是因为式(16)满足γ=p,故p(p-γ)-γ=-γ<0,因此此时无瘤平衡点P0(1,0)必是不稳定的。
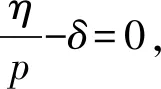
(17)

定理2 系统(5)在无瘤平衡点P0(1,0)局部渐近稳定,当满足以下任意条件之一:
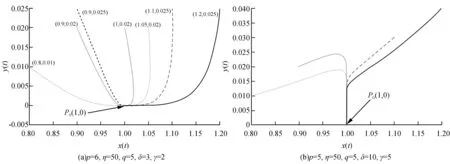
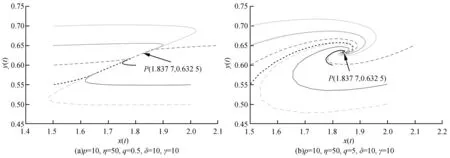
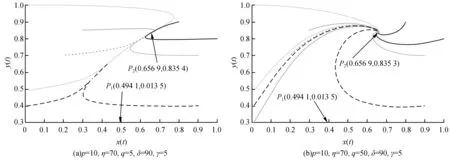
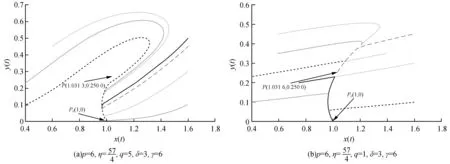
1)γ 系统(5)在无瘤平衡点P0(1,0)不稳定,当满足以下任意条件之一: 1)γ>p; 对于第2部分讨论的任意有瘤平衡点P(x*,y*),系统(5)在P(x*,y*)处的Jacobi矩阵为: (H2)a11+a22<0。 (H3)a11a22-a12a21>0。 (H4)a11a22-a12a21=0。 定理3 当条件(H2)和(H3)成立时,系统(5)在有瘤平衡点P(x*,y*)处是局部渐进稳定的。 令u1=x-x*,v1=y-y*并代入系统(5)中,得 (18) 其中, 对系统(18)作线性变换 得 (19) 其中, ξ2N(z1+ξ2w1,ξ1z1+w1)), ξ1M(z1+ξ2w1,ξ1z1+w1))。 类似于3.1节,求得式(19)在原点的局部中心流行为 (20) 其中, 将式(20)代入式(19)的第二式,有 o(w2)≜Qw2+o(w2)。 (H5)Q<0。 定理4 当条件(H2)和(H4)成立时,系统(5)存在高阶有瘤平衡点P(x*,y*),当条件(H5)成立时,有瘤平衡点是局部渐近稳定的。 最后分析稳定的有瘤平衡点P(x*,y*)的类型。定理3和定理4给出存在局部渐进稳定的有瘤平衡点,对于系统(5)和这样的有瘤平衡点,当κ=trJ(P)2-4detJ(P)<0,P是焦点;当κ≥0,P是结点。 本节利用Matlab对第3节的结论进行数值模拟分析。 对于系统(5),选取参数p=6,η=50,q=5,δ=3,γ=2,和参数p=5,η=50,q=5,δ=10,γ=5进行数值模拟,分别如图1(a)和图1(b)所示,均收敛于点P0(1,0),这表明无瘤平衡点P0(1,0)局部渐近稳定。 图1 系统(5)在P0(1,0)附近的轨线Fig.1 The phase portraits of system(5) around P0(1,0) 选取参数p=10,η=50,q=0.5,δ=10,γ=10,如图2(a)所示,存在有瘤平衡点P=(1.8377,0.6325),且该平衡点为稳定的结点。此时l1<0,l2=0,条件(H2)、(H3)均成立,κ>0;更换参数值q=5,其他参数值不变,如图2(b)所示,有瘤平衡点P=(1.8377,0.6325)是稳定的焦点。此时l1<0,l2=0,条件(H2)、(H3)均成立,κ<0。 选取参数p=10,η=70,q=5,δ=90,γ=5,此时Δ<0,l2>0,如图3(a)所示,系统(5)存在两个不同的有瘤平衡点,即P1=(0.4941,0.0135)和P2=(0.6569,0.8353)。P1不稳定,此时平衡点P1满足条件(H2),detJ(P)<0;P2为稳定的结点,此时该平衡点满足条件(H2)、(H3)和κ>0。更换参数值q=50,其他参数不变,如图3(b)所示,平衡点P1不稳定,此时P1满足条件(H2),detJ(P)<0;平衡点P2为稳定的焦点,此时该平衡点满足条件(H2)、(H3)和κ<0。 图2 系统(5)在有瘤平衡点P的局部稳定性Fig.2 The local stability of system (5) at the tumor equilibrium point P 图3 系统(5)在有瘤平衡点P1和P2的局部稳定性Fig.3 The local stability of system (5) at the tumor equilibrium points P1 and P2 图4 系统(5)在无瘤平衡点P0和有瘤平衡点P的局部稳定性Fig.4 The local stability of system (5) at the tumor-free equilibrium point P0 and the tumor equilibrium point P 本文研究了一类具抗原性和简化Holling-IV型肿瘤与免疫系统相互作用的模型。首先对模型通过无量纲化处理以减少参数,简化模型。接着分析了平衡点的存在性。然后在平衡点存在的范围内研究了各个平衡点的局部动力学性质。分析结果表明,模型会出现无瘤平衡点和有瘤平衡点同时稳定的情况。这种双稳态的现象表明肿瘤的增长与初始状态有关,当肿瘤细胞和效应细胞的初值均很小时,或肿瘤初值很小,效应细胞初值很大时,肿瘤细胞最终消失;当肿瘤初值很大,而效应细胞初值很小时,或肿瘤细胞和效应细胞初值均很大,肿瘤趋于正平衡点。由此可见,尽早发现肿瘤细胞的出现,有助于肿瘤的消失。接着,本文给出了当有瘤平衡点稳定时,该平衡点是焦点还是结点的条件。最后利用Matlab进行数值模拟,支撑理论分析。3.2 有瘤平衡点的稳定性
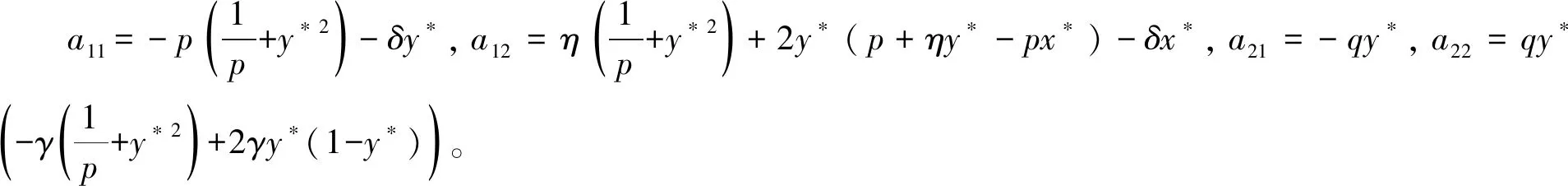

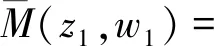
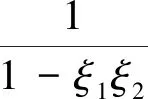
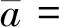
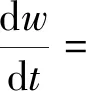
4 数值模拟
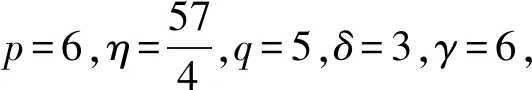

5 结 论
