MgB2的高压效应研究

桑丽娜，李敏娟，张义邴，朱红妹，李文献，蔡传兵,*

(1. 上海大学 材料科学与工程学院材料研究所，上海 200072；2. 上海大学 理学院物理系，上海市高温超导重点实验室，上海 200444)

0 引言

2001年具有超导转变温度Tc为39 K的MgB2超导的发现不但突破了传统常规超导体微观理论(BCS)预言的简单金属间化合物的超导转变温度极限(约24 K)，还具有许多“传统”高温超导材料不具备的超导特性。其相对较高的Tc、多能带结构、无晶界弱连接问题以及低成本，很快引起了国际物理学界的广泛关注。但是干净的MgB2超导材料的磁通钉扎能力相对比较弱，在外加磁场时，电流密度(Jc)急剧下降，载流能力差。目前所知，化学掺杂、高能离子辐照或注入以及高压已成为引入缺陷来提高Jc的三种主要方法。通过化学掺杂可增加磁通钉扎中心密度进而实现Jc的提高；高能离子辐照的处理同样是引入点状或柱状缺陷等来增加钉扎密度。而过量的掺杂以及高剂量的辐照同时也在破坏样品的超导电性，以致失超。由于前期我们组研究的Sr4V2O6Fe2As2[1]、NaFe0.97Co0.03As[2]和(Ba,K)Fe2As2[3]、Fe1-xCoxSe0.5Te0.5[4-5]等铁基超导体的超导电性Tc在高压效应下都得到了显著提高[6-7]。而且高压除了上述对Tc的影响之外，对于Jc和磁通钉扎的增强也具有很多的优点：1)减小晶格参数并缩小晶胞尺寸，降低各向异性；2)改善晶界的连接性，克服弱连接问题；3)通过增加缺陷引入更多钉扎中心，导致Jc进一步提高。为了研究高压对MgB2的影响，以及其在压力下的钉扎机制，本文做了详细的实验以及分析。

1 实验方法

我们采用固相熔融法成功制备了MgB2块材。首先，称量高纯度(Alfa Aesar，99.99%)Mg和B粉末，按化学计量混合，并在充满氩气保护的手套箱内将粉末充分研磨，然后将之压制成圆片，在氩气气氛下进行烧结，以5 ℃/min的速度加热到800 ℃并在该温度下保持1 h，随后冷却至室温，即可得到MgB2超导块材。我们采用综合物性测量系统(PPMS，Quantum Design)进行了不同温度下的磁性测量。根据Bean临界态模型计算临界电流密度Jc，Jc= 20ΔM/a(1-a/3b)，其中a和b是垂直于外加磁场方向样品的宽度和长度，ΔM是样品MH磁滞回线升场和降场的磁化强度之差，单位emu/cm3。

2 实验结果与讨论

图1(a)显示了MgB2样品的零场冷(ZFC)和场冷(FC)的磁化曲线M-T。样品在压力1.2 GPa下，Tc从37.5 K降到35.8 K。图1(b)显示了样品在无压力时不同温度下的磁滞回线(M-H曲线)，我们可以很清晰地在低温观测到磁通跳跃现象，该现象主要是因为大电流或在高磁通密度梯度时发生。低温下的磁化Jc比较大造成了洛伦兹力就比较大，而低温下用于导热的正常态电子相对比较少，磁通运动产生的热量无法快速导热出去，样品局部温度会持续上升，又会带来磁通的进一步运动，进而表现出了磁通跳跃现象。随着温度的升高，这一现象会逐渐消失，如图所示。根据Bean模型，得出不同压力下的Jc。图2(a-d)显示了样品在不同温度和压力下的Jc-B曲线，P= 0 GPa和1.2 GPa。在2 K时，样品自场Jc从2.5 × 105A/cm2(0 GPa)降到1× 105A/cm2(1.2 GPa)，尤其是在高温高场下下降更加明显。

图1 (a)MgB2不同压力下零场冷和场冷的磁化曲线M-T；(b)MgB2不同温度下的MH磁滞回线Fig. 1 (a) Temperature dependence of zero-field-cooled and field-cooled (ZFC and FC) moments at different pressures for MgB2; (b) M-H measurements of MgB2 sample at different temperatures

图2 样品分别在0 GPa和1.2 GPa压力下(a)2 K；(b)10 K；(c)15 K；(d)20 K的Jc随磁场的变化Fig. 2 Jc vs. field under different pressures at 2 K, 10 K, 15 K, and 20 K for MgB2

除了Jc的大幅降低，我们发现不可逆线Hirr在压力下向低温低场移动也非常显著，如图3所示。同时，根据磁化强度随外加磁场的变化可以大致得出下临界场Hc1，压力同样也导致了Hc1的降低。由金兹堡朗道理论定义的两个参数：超导相干长度ξ和穿透深度λ，其与上临界场和下临界场的关系为：Hc1(T)=Φ0/4πλ(T)2、Hc2(T)=Φ0/2πξ(T)2，说明压力效应增加了MgB2样品的穿透深度和超导相干长度，即涡旋的半径以及磁场的衰减长度增加，这与高压对铁基超导的影响完全不同，接下来我们来进一步探究高压对MgB2钉扎机制的影响。

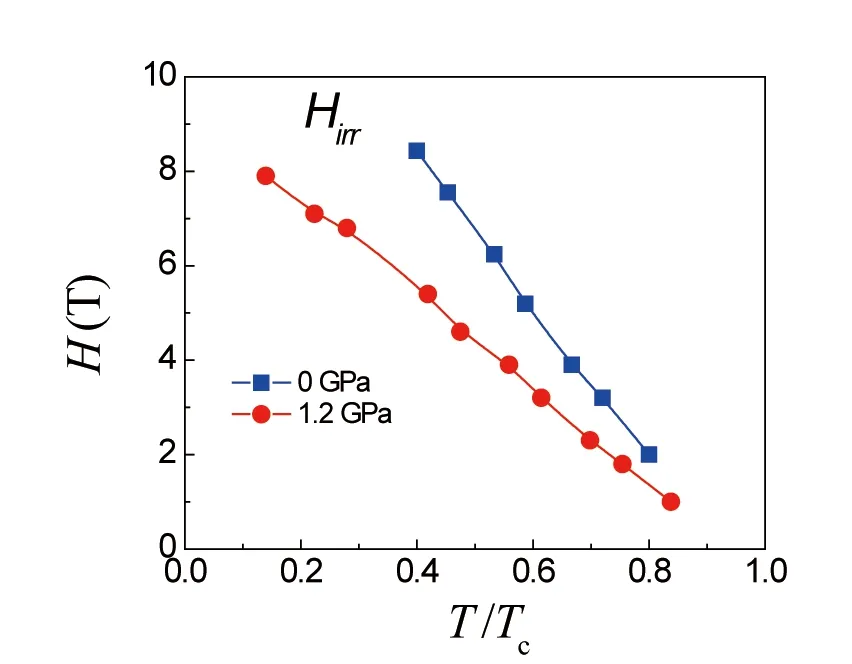
图3 不同压力下Hirr随约化温度变化的依赖关系Fig. 3 Hirr vs. T/Tc for MgB2 at 0 and 1.2 GPa

根据集体钉扎理论，外加磁场低于H*时，Jc几乎不受影响，单磁通钉扎机制占主导。样品中缺陷的分布和磁通线的相互作用会引起磁通线的钉扎。依据集体钉扎理论，有两种主要的钉扎机制：δTc钉扎(Tc中的随机分布空间变化)和δ钉扎(电荷载流子平均自由路径中的空间变化)，说明单涡旋钉扎时，Jc显示出与温度有关的不同行为的钉扎机制。为了进一步研究样品中的钉扎机制行为，我们对临界电流密度做了进一步的分析[8-10]。

Hsb=JsvHc2

(1)

Jsv是单磁通钉扎区域的临界电流密度，Hc2是上临界磁场。在高磁场区域(即高于H*)，Jc(H)遵循下面的规律：

(2)

温度和H*的关系可用下列公式表示：

(3)

v为2/3和2时分别代表δTc或者δ钉扎机制。约化温度t=T/Tc。把公式(3)代入公式(1)，Jsv分别遵循以下规律[8-9]：

δ钉扎:Jsv(t)/Jc(0) = (1-t2)5/2(1+t2)-1/2

(4)

δTc钉扎:Jsv(t)/Jc(0) = (1-t2)7/6(1+t2)-6/5

(5)

图4(b)的结果显示压力改变了MgB2的钉扎机制，由原先的δTc钉扎转变为δ钉扎。MgB2多晶块体、薄膜和单晶中主要的钉扎机制通常是δTc钉扎占主导。我们知道超导的相干长度与载流子的平均自由程成正比。因此，压力增强了MgB2中的平均自由程的钉扎，这也说明了压力降低了MgB2的临界电流的原因。

图4 (a)15 K时在0 GPa和1.2 GPa下Jc随磁场的变化以及H*的获得；(b)H*(T)/H*(0)与约化温度t = T/Tc的依赖关系Fig. 4 Jc vs. field at 15 K for MgB2, H*, were obtained from the experimental Jc(B) curves; (b) Normalized measured H*(T)/H(0) vs. t = T/Tc under different pressures for MgB2 sample

另外，我们还研究了钉扎力密度FP=Jc×B。根据Dew-Hughes钉扎模型，由公式fp∝hp(1-h)q进行拟合(h=H/Hirr)，不同的p、q值代表不同的钉扎机制。p= 1，q= 2代表点钉扎机制，而p= 1/2，q= 2代表面钉扎类型，结果如图5所示，无论压力大小，MgB2样品中的主要钉扎来自于面钉扎。

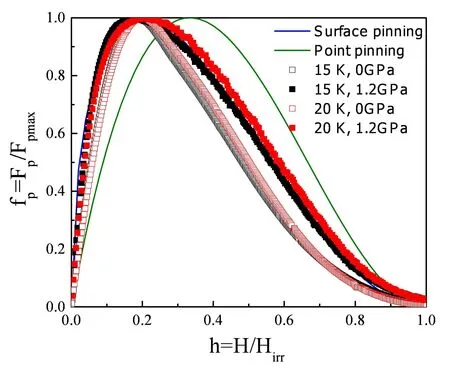
图5 温度15 K和20 K时在0 GPa和1.2 GPa下的约化钉扎力fp = Fp/Fpmax与约化磁场h= H/Hirr的依赖关系Fig. 5 Plots of the normalized pinning force (fp = Fp/Fp,max) vs. h = H/Hirr for MgB2 sample at 0 and 1.2 GPa, in good agreement with surface pinning

通过磁弛豫的测量，即磁化强度M随时间t的变化关系，可以得到表征磁通蠕动快慢的弛豫率S，S= |dlnM/dlnt| (其中t是时间)[11]，还能得出钉扎能U0。图6(a)(b)是在1 T时0 GPa和1.2 GPa压力下不同温度的磁化强度M与时间t的双对数变化曲线。

为了进一步探索磁通钉扎涡旋的运动，我们采用扩展的梅列方法[12-13]，激活能如下所示：

U=-Tln[dJ(t)/dt]+CT

(6)

C是拟合参数，C=ln(Bωa/2πR)，ω是涡旋跳跃的频率，R是样品的半径，a是跳跃间距[14-16]。为了获得U对J的平滑依赖性，我们使用U/G(T)比例关系来描述钉扎能的变化，G(T)=[1-(T/Tc)2]1.5[17]。在图6(c)中，我们观察到所有的曲线可以很好地缩放在一起。指数μ是一个关键参数，表征了磁通格子的维数和磁通束的大小[18]，当μ= 1/7，5/2，7/9时分别对应于单涡旋蠕动、小磁通束、大磁通束尺寸的钉扎[8,11,19]。

图6 MgB2在1 T不同温度下磁化强度M与时间t的双对数依赖关系(a)0 GPa 和(b)1.2 GPa；(c)P = 0 GPa和P = 1.2 GPa时，使用Maley分析确定的钉扎能在1 T时随临界电流密度的变化，实线是倒幂函数模型U(J)=U0[(Jc0/J)μ-1]的拟合Fig. 6 Time dependence of magnetization during 1 h at different temperature with H=1 T, (a) 0 GPa, (b) 1.2 GPa. (c) Current density dependence of the activation energy of the MgB2 sample with and without pressure: at 1 T, as determined using the Maley analysis. The solid lines are fits of the data to the inverse power-law form (J)=U0[(Jc0/J)μ-1]

根据Maley方法，在0 GPa和1.2 GPa时，1 T下拟合的μ值分别为0.55和0.6，表明MgB2样品里的涡旋蠕动尺寸主要是大磁通束尺寸的磁通钉扎。综上所述，压力加快了磁通的蠕动，降低了有效钉扎能和临界电流密度，磁通束尺寸的大小变化不大。

3 结论

研究了高压对MgB2块材超导的Tc、Jc、Hirr以及钉扎机制的影响。结果显示高压降低了样品的Tc、Jc以及不可逆场Hirr。压力使样品中Tc随机分布空间变化的δTc钉扎转变为了电荷载流子平均自由路径中空间变化的δ钉扎。压力还会增加各向异性，同时导致相干长度和平均自由程的增加。通过磁弛豫的测量，结果显示压力加快了磁通的蠕动，降低了有效钉扎能和临界电流密度，磁通束尺寸的大小变化不大。