L波段高性能双通带高温超导滤波器
2023-01-09张亚辉陆勤龙王生旺
禹 潇,张亚辉,宾 峰,陆勤龙,王生旺
(1.中国电子科技集团公司第十六研究所,合肥 230088;2. 中国电子科技集团公司超导电子技术重点实验室,合肥 230088)
0 引言
近年来,随着通信、雷达、深空探测等技术的发展,可支持多通信协议和高质量通信的多信道通信是一个重要趋势。作为多信道接收机的重要部件之一,多通带滤波器的性能可以直接影响接收机的性能。由于超导滤波器具有低插损、高带外抑制和带边陡度等优异性能,应用于接收机时可有效提高接收机的信噪比和抗干扰能力,吸引着越来越多的关注。
目前双通带滤波器最常用的设计方法有三种。第一种方法是通过组合多个滤波器来设计双通带滤波器,在文献[1]中,一个带阻滤波器和一个带通滤波器被直接组合成为一个双通带滤波器,在文献[2]中,两个带通滤波器使用同一个馈电结构连接在一起形成一个双通带滤波器。这种方法具有设计简单、原理清晰、可独立控制不同通带的优势,但是这种方法得到的滤波器体积一般较大。第二种方法是采用优化综合耦合矩阵的方法[3],这种方法的好处是逻辑清晰、结构紧凑,但是这种方法得到的耦合矩阵往往比较复杂,有些耦合矩阵很难用物理电路实现。第三种方法是基于多模谐振器来实现,如阶跃阻抗谐振器(stepped-impedance resonators, SIRs)[4-5]和枝节加载型谐振器(stub-loaded resonators, SLRs)[6-7]等,这种方法得到的多通带滤波器结构紧凑,并可以实现多个不同的带宽。Zhou等人[7]曾使用SLRs完成了一款L/S波段的双通带超导滤波器的研制,该滤波器的中心频率分别为1 490 MHz(带宽40 MHz)和2 340 MHz(带宽80 MHz),并通过引入传输零点提高了滤波器的带边陡度。Lu等人[8]也使用SLRs完成了一款S波段的四阶双通带超导滤波器的研制,中心频率分别为2 450 MHz(相对带宽8%)和3 500 MHz(相对带宽5%)。此外,还有Song等人[9]、Heng等人[10]均采用这种方法完成了双通带超导滤波器的研制。总的来说,双通带超导滤波器正朝着小型化、高选择性、极限带宽、均衡群时延等方向发展。
本文详细介绍了一款基于SLRs的八阶双通带超导滤波器的研制过程。该滤波器要求中心频率分别为1 220 MHz和1 580 MHz,1 dB带宽分别大于145 MHz和80 MHz;要求在960 MHz和1 900 MHz处带外抑制均大于60 dB,在1 360~1 460 MHz之间大于40 dB。此外,该滤波器还要求带内任意20 MHz的群时延波动均要小于4 ns。
1 谐振器设计与分析
从设计指标可以看出,该双通带滤波器既要兼顾带外的频率选择性要求又要有平坦的带内群时延波动。为了满足设计要求,本文采用八阶切比雪夫滤波器并引入传输零点的方式来实现。由于滤波器群时延波动最大部分为通带边缘部分,因此在设计时将低频通带的下边频和高频通带的上边频展宽20 MHz,低频通道的上边频和高频通带的下边频展宽10 MHz,这样不仅能提高带内群时延平坦度,还能减小温度以及仿真介电常数数值不准确造成的频率偏移影响。边带的拓宽值是根据以往的工程经验给出,经过仿真可以满足要求,也可以根据仿真结果灵活选择其他数值。根据广义耦合矩阵综合理论[11]可得耦合系数和外部品质因数如下表1所示。

表1 双通带超导滤波器耦合系数和品质因数Table 1 Parameters of the properties of the system
根据设计要求和耦合矩阵,本文所提出的SLR版图如图1(a)所示。该谐振器主要由上半部分的强耦合半波长谐振器和一个加载枝节组成,谐振器线条宽度均为0.1 mm。从图中可以看出谐振器的上半部分沿着中轴线对称,枝节加载在轴线位置,其等效电路图如图2(a)所示。

图1 (a) 双模SLR版图;(b) 奇模谐振时的电流分布;(c) 偶模谐振时的电流分布Fig. 1 (a) Layout of the dual-mode SLR; (b) Current distribution of odd mode at resonance; (c) Current distribution of even mode at resonance
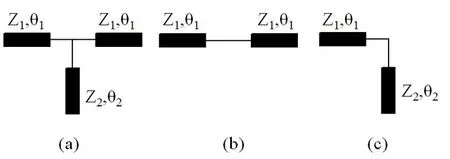
图2 (a) 谐振器等效电路;(b) 谐振器在奇模时的等效电路;(c) 谐振器在偶模时的等效电路Fig. 2 (a) Equivalent circuit; (b) Odd-mode equivalent circuit; (c) Even-mode equivalent circuit
根据多模传输线理论和奇偶模分析法,该谐振器有奇模和偶模两种谐振模式。当谐振器在奇模处谐振时,谐振器的加载枝节可以等效为开路,此时谐振器可以看作只有上半部分的半波长谐振器,其等效电路图如图2(b)所示。谐振器在偶模处谐振时,加载枝节处可以等效为短路,此时谐振器可以看作上半部分的一半加上加载枝节组成的谐振器,等效电路图如图2(c)所示。在弱外部耦合条件下,我们使用Sonnet软件对谐振器分别在奇模和偶模谐振频率处的电流分布进行了模拟仿真,结果如图1(b)和1(c)所示,从图中可以看出在奇模谐振频率处,电流主要分布在谐振器上半部分,而在偶模谐振频率处,电流几乎分布在整个谐振器上,这与前面的分析也是一致的。
我们对相邻谐振器耦合时的频率响应和相位曲线进行了仿真,结果如图3所示,从图中可以看出曲线上有四个明显的谐振峰,分别为奇模和偶模耦合时的谐振峰。此外,从图中可以看出,谐振峰中间的相位均为负值。因此,当该谐振器与相邻谐振器进行耦合时,奇模和偶模可以同时形成两个通带,由于加载枝节只影响谐振器的偶模谐振频率,因此也可以独立地调节这两个通带。
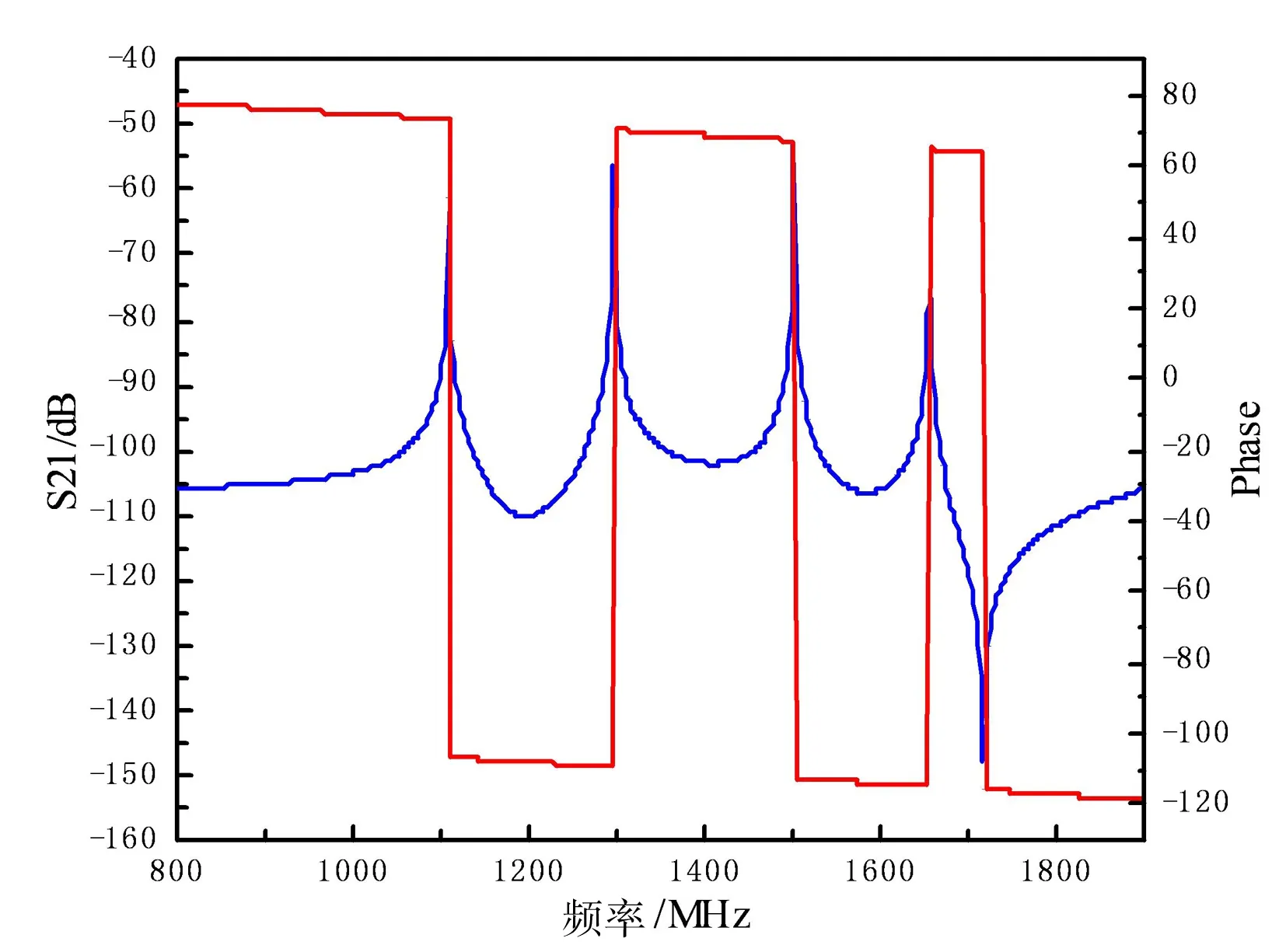
图3 相邻谐振器耦合时的频率响应和相位曲线Fig. 3 The frequency and phase response of the coupling resonators
根据表1中的耦合系数,低频段的通带需要更强的耦合强度,因此谐振器的奇模用于构建滤波器低频段的通带1,偶模用于构建高频段的通带2。两个通带相邻谐振器的耦合系数与谐振器间距的仿真结果如图4(a)和4(b)所示,从图中可以看出,两个通带的耦合系数几乎都随着s1的增大而线性减小。但是当s1不变时,通带1的耦合系数不受s2的影响,而通带2的耦合系数随着s2的增大而减小,这也与前面的分析结果相一致。从图中的耦合系数变化趋势可以看出,该谐振器可以满足表1的耦合系数要求。在滤波器版图设计时,先通过调节s1,使通带1的耦合系数满足要求,然后再调节s2,使通带2的耦合系数满足要求。
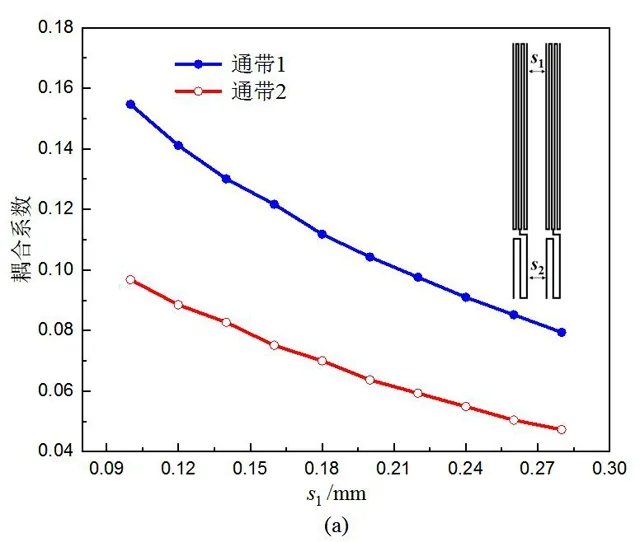
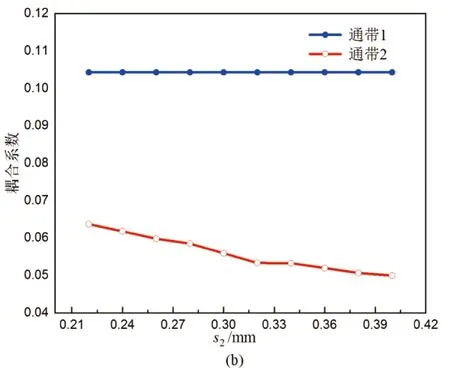
图4 (a) s1和耦合系数的关系;(b) s1 = 0.2 mm时,s2和耦合系数的关系Fig. 4 (a) Relationship between s1 and coupling coefficient; (b) Relationship between s1 and coupling coefficient when s1 = 0.2 mm
除了相邻谐振器之间的主耦合之外,谐振器还要满足表1中的交叉耦合系数要求。本文所提出的交叉耦合结构如图5所示,这种结构所得到谐振峰之间的相位为正值,与相邻谐振器耦合谐振峰之间的相位相反。交叉耦合系数主要受l1以及耦合线与谐振器线条间距影响,为了降低设计难度,在仿真时耦合线与谐振器线条间距设置为固定值,只调节l1,仿真结果如图5所示。为了表示相位的不同,交叉耦合系数取值为负值,正负号不表示数值的大小。从结果可以看出,耦合系数随着l1的增大而增大,且数值可以满足表1的需求。

图5 交叉耦合系数与l1之间的关系Fig. 5 Relationship between cross coupling coefficient and l1
2 滤波器设计
根据表1中的耦合矩阵,谐振器间的耦合系数确定以后,只需要得到输入/输出结构即可得到滤波器的版图。为了同时得到两个通带所需要的外部品质因数,滤波器采用分叉枝节馈线分别连接SLR上下部分的方式,如图6(a)所示。由于馈线直接连接在谐振器上会直接影响谐振频率,为了保证谐振频率相同,谐振器的尺寸与滤波器中间部分的谐振器的尺寸相比变化较大。两个通带的外部品质因数Q1和Q2主要由馈线的相对位置h1、h2和h3来决定,其关系如图6(a)、6(b)、6(c)所示。从图中可以看出,h1、h2和h3对Q2均有影响,但是只有h2对Q1有影响,因此在设计时,优先调节h2,然后再调节h1和h3,这样即可快速得到所需要的外部品质因数。

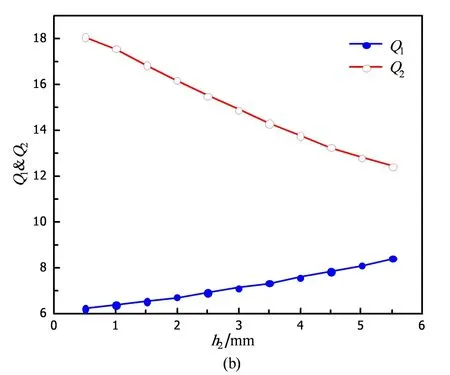
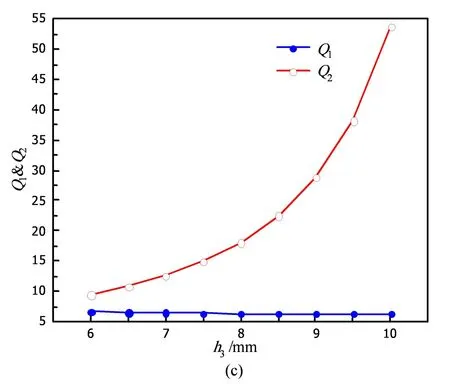
图6 (a) Q值与h1的关系;(b) Q值与h2的关系;(c) Q值与h3的关系Fig. 6 (a) The relation between Q and h1; (b) The relation between Q and h2; (c) The relation between Q and h3
确定了谐振器耦合和输入/输出结构以后,即可进行物理电路的搭建。电路仿真使用Sonnet软件,仿真方法采用单端口群时延法[12],由于该方法已非常成熟,此处不再赘述。滤波器的最终版图如图7所示,包含接头的电路尺寸约19.02 mm×21.12 mm。超导滤波器S曲线和群时延曲线的最终仿真结果如图8(a)和8(b)所示,从图中的仿真结果可以看出,矩形系数和群时延波动均符合设计要求。
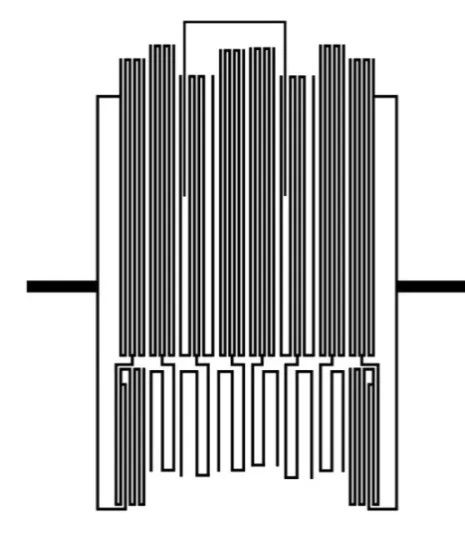
图7 超导滤波器版图Fig. 7 Layout of the HTS filter

图8 超导滤波器实物图Fig. 8 Photograph of the filter
3 滤波器制作与测试
滤波器电路采用2英寸的MgO衬底的双面YBCO薄膜通过光刻技术制作而成。光刻技术是一种图形复印和化学腐蚀或离子束刻蚀相结合的加工技术,在半导体器件和微型集成电路制造上应用非常广泛。光刻之前,首先需要制作掩膜版,掩膜版制作完成后即可进行超导滤波器电路的刻蚀,高温超导电路的刻蚀主要包括以下八个步骤:清洁、涂胶、前烘、曝光、显影、后烘、腐蚀、去胶。光刻好的电路封装在金属屏蔽盒里,采用标准的SMA射频接头与外部电路相连,实物图如图8所示。
超导滤波器封装完成后,使用小型制冷机配合真空杜瓦进行冷却,采用网络矢量分析仪进行测试,测试结果和仿真结果的对比如图9所示。从图中可以看出,滤波器的测试结果与仿真结果几乎一致,这也说明了滤波器的光刻及封装工艺精度较高,对滤波器的影响较小,可以满足生产要求。图9(a)为超导滤波器S参数测试结果与仿真结果的对比图,测试结果表明1 dB通带分别为1 121~1 321 MHz、1 527~1 648 MHz。结果中有四个较明显的传输零点,分别在1 000 MHz、1 368 MHz、1 427 MHz和1 700 MHz处。由于传输零点的作用,滤波器在960 MHz和1 900 MHz处带外抑制均大于60 dB,在1 360~1 460 MHz之间带外抑制均大于40 dB,带外抑制和通带范围均满足设计要求。图9(a)中的两个放大图分别为两个通带的S21曲线测试结果,从图中可以看出,滤波器的最小插损<0.1 dB,带内最大波动<0.5 dB。图9(b)为滤波器的群时延仿真和测试结果,从两个通带的放大图中可以看出,在通带内任意20 MHz的群时延波动均<4 ns。滤波器在两个通带内的群时延最大波动处均在通带边缘位置,由于两个通带均进行了展宽,特别是第2个通带的右边频展宽较多,因此群时延可以满足设计要求。由于传输零点的作用,即使在适当展宽通带的情况下,带外抑制依然可以满足设计要求。
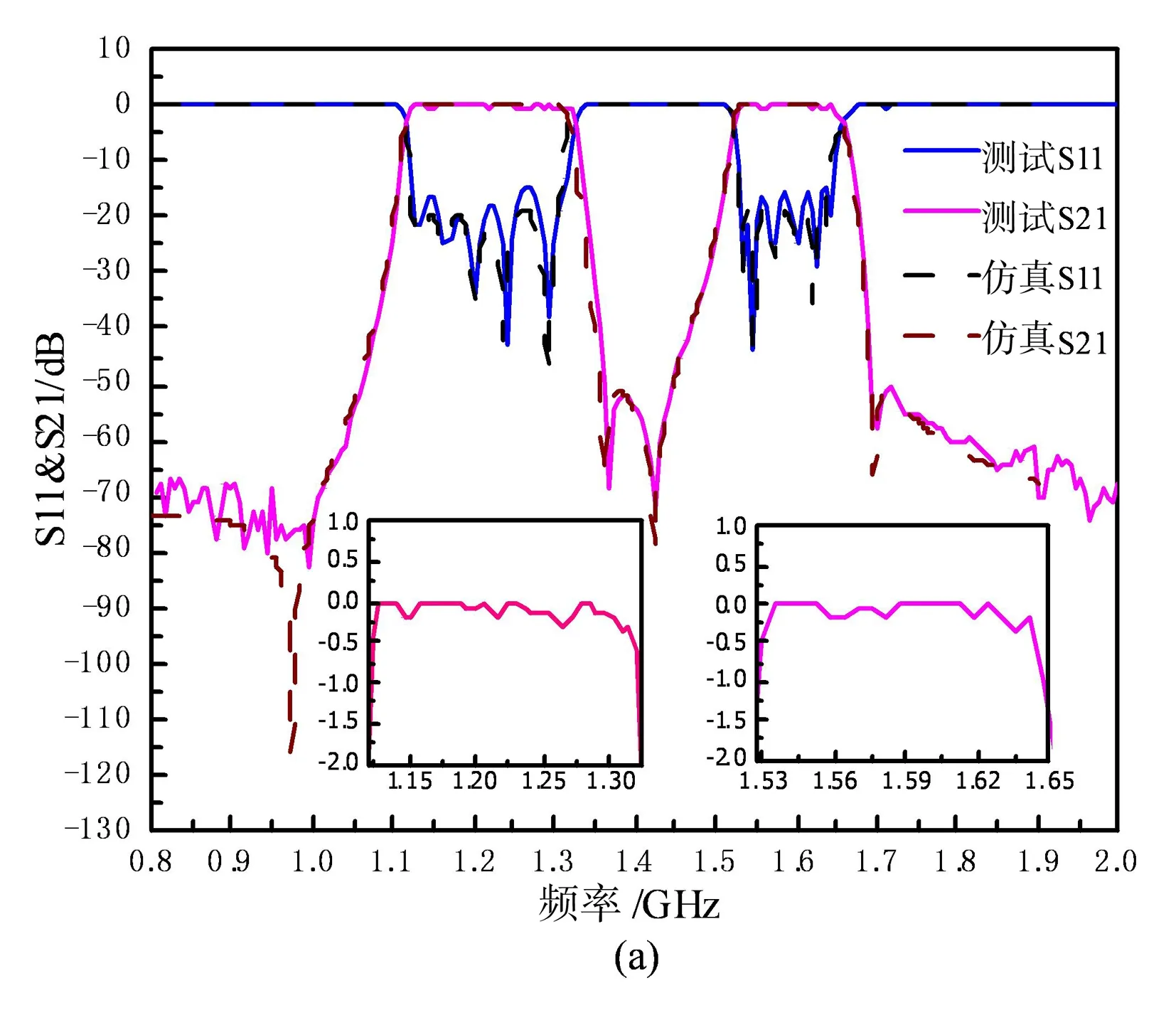
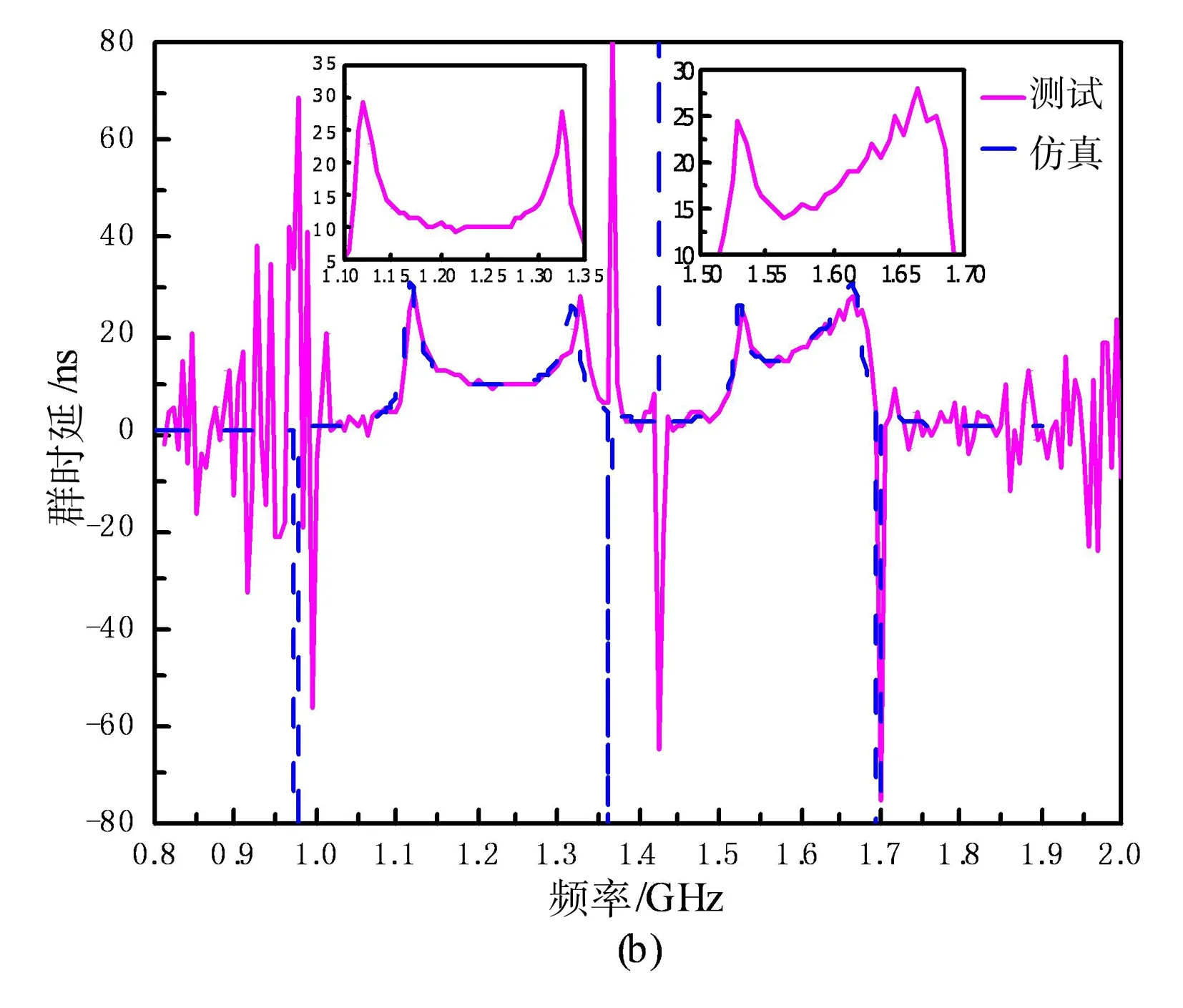
图9 滤波器仿真和测试结果 (a) S曲线;(b) 群时延Fig. 9 Simulated and measured results of the filter (a) S-curve; (b) Group delay
4 结论
本文介绍了一种适用于L波段的双频SLR,并对该谐振器的耦合特性进行了详细分析。基于该谐振器和分叉枝节直接加载馈电结构,完成了一款八阶高性能双通带超导滤波器的研制。该滤波器包含接头的电路尺寸仅约19.02 mm×21.12 mm,滤波器测试结果与仿真结果基本一致,可以满足设计要求。
