极限状态法和容许应力法用于重载铁路钢筋混凝土梁受力性能评价的对比

许宏伟 于子杰 刘永前 李勇

1.石家庄铁道大学道路与铁道工程安全保障教育部重点实验室，石家庄 050043；2.石家庄铁道大学河北省大型结构健康诊断与控制重点实验室，石家庄 050043

收稿日期：2022-04-30；修回日期：2022-09-26

基金项目：河北省重点研发计划(20375410D,21375403D)；河北省自然科学基金(E2020210017)；石家庄铁道大学优秀青年科学基金（201801）；河北省研究生创新研究基金（CXZZSS2022109，CXZZSS2022110）

第一作者：许宏伟(1975—)，男，讲师，硕士。E-mail：xuhw@stdu.edu.cn

通信作者：刘永前(1969—)，男，教授，博士。E-mail：liuyq_stdu@126.com

国内在役普速铁路桥涵主要根据容许应力法进行设计［1-3］。该方法基于线弹性理论，以桥梁危险截面最不利点的计算应力小于等于材料的容许应力为准则，计算简单方便，在我国铁路桥梁建设中发挥了巨大作用［4-5］。然而既有设计规范未对钢筋混凝土梁的强度计算进行规定。

为了适应铁路桥涵技术的不断发展并进一步提高桥梁设计水平，根据不同材料特征和荷载种类采用不同分项系数的极限状态法尝试应用于铁路桥梁设计［6-8］。该设计方法全面考虑了影响结构安全的各种因素的差异，使设计结果更加可靠。文献［9］和文献［10］分别对连续梁桥进行容许应力法和极限状态法的对比研究，认为采用容许应力法设计理念更加保守；文献［11］对钢筋混凝土轨道梁进行两种设计方法的对比分析，认为二者计算结果的差异与配筋率和材料强度有关。

现有研究都是基于理论计算和精细化分析，缺乏试验验证［12-14］。因此，本文选取根据容许应力法设计12 m钢筋混凝土T梁（专桥（88）1024），分别根据TBJ 2—1985《铁路桥涵设计规范》［15］和Q/CR 9300—2018《铁路桥涵设计规范（极限状态法）》［16］进行对比分析，并通过静力加载破坏试验［17-19］测试不同荷载下足尺钢筋混凝土T梁钢筋应力状态，以及梁体的变形和裂缝发展情况，探究极限状态法和容许应力法用于评价重载铁路12 m钢筋混凝土T梁桥受力性能的异同，为铁路桥梁设计提供参考。

1 工程概况

因裂缝宽度超限、钢筋锈蚀、混凝土劣化等病害，更换重载铁路上一片钢筋混凝土T梁，并将其作为试验对象。根据各劣化因素对梁体承载力影响程度的权重，估算混凝土承载力评定系数为1［20］。试验梁建于1998年，全长12.5 m，计算跨径12 m，腹板宽1.1 m，梁高（不含挡砟墙）0.85 m，挡砟墙高300 mm，挡砟块高250 mm，挡砟块用砂浆砌于挡砟墙上，挡砟墙上设置10 mm断缝。断缝采用10 mm厚油毛毡填实，防止桥面水从断缝流下。桥面单侧设人行道，人行道宽1.05 m。人行道角钢支架与预埋在挡砟墙处T形钢连接。试验T梁的几何尺寸及配筋见图1。梁体采用350号混凝土（相当于C33），纵筋采用ϕ25的T20MnSi钢筋（相当于HRB335钢筋），跨中截面配筋率2.4%，箍筋采用ϕ8的T20MnSi钢筋（相当于Q235钢筋）。

图1 试验T梁几何尺寸与配筋（单位：mm）

2 基于容许应力法的设计计算

根据TB 10002.1—2005《铁路桥涵设计基本规范》，容许应力法的荷载组合采取主力组合，在组合时无分项系数。主力主要包括梁体自重、二期恒载和列车活载。梁体自重折算成29.56 kN/m的均布荷载。二期恒载主要考虑道砟、轨道、枕木、人行踏板的重量，道砟按重度21.0 kN/m3计算；钢轨按75 kg/m轨计算，计算均布荷载为0.7 kN/m；按Ⅱ型混凝土枕木计算，荷载为2.3 kN/m；人行踏板按5 kN/m计算。综合计算得到二期恒载折算均布荷载为26.8 kN/m。主力组合为1.0倍自重+1.0倍二期恒载+1.0倍列车活载。试验桥梁按照中—活载进行设计，实际主要常态化开行C64、C70和C80列车。随着重载运输的快速发展，列车轴重显著提高，开始部分开行KM98列车。通过计算可知自重在跨中产生的弯矩为532 kN·m，二期恒载产生的弯矩为483 kN·m。考虑1.286的动力系数，不同列车活载及容许应力法荷载组合的弯矩见表1。

TBJ 2—1985对铁路桥梁规定了应力、裂缝宽度及挠度的容许值。根据容许应力法设计理念要求应力、裂缝宽度及挠度不超过容许值，即钢筋混凝土梁在弯曲受压的情况下钢筋容许应力［σs］为180 MPa，混凝土容许应力［σc］为12.12 MPa。对于一般大气条件下，无防护措施的结构裂缝宽度容许值［ωc］为0.2 mm。对于简支钢筋混凝土结构桥因列车竖向静活载（不计冲击）引起的竖向挠度容许值为l0/800（l0为梁的计算跨径）。容许应力法计算结果见图2。

表1 不同列车活载及容许应力法荷载组合的弯矩kN·m

图2 容许应力法计算结果

根据图2中混凝土应力、钢筋应力和裂缝宽度容许值反推计算，可以得到在1.0倍自重+1.0倍二期恒载+1.0倍列车活载的荷载组合下，满足应力要求时梁的容许最大弯矩为2 496 kN·m，满足裂缝宽度要求时梁的容许最大弯矩为3 410 kN·m。同时满足应力要求和裂缝宽度要求的容许弯矩为2 496 kN·m。在不同列车活载组合作用下，混凝土应力、裂缝宽度和列车静活载下挠度均满足规范要求。与表1对比可知，T梁可以满足C64、C70和C80的运行要求，但不能满足KM98的运行要求。

3 极限状态法的设计理念

极限状态法的设计理念是桥梁根据正常使用极限状态（应力、挠度和裂缝宽度）和承载能力极限状态（承载能力）进行设计，设计时考虑永久作用和基本可变作用。永久作用包括结构自重和结构附加重力（道砟桥面），可变作用包括列车活载。其中计算承载能力、应力和挠度采用式（1）的组合方式，计算裂缝宽度采用式（2）的组合方式。

式中：Sd为作用组合的效应设计值；γ0为结构重要性系数，取1.0；S为作用组合的效应函数；γGi为第i个永久作用的分项系数；Gik为第i个永久作用的标准值；γQ1为主导可变作用的分项系数；Q1k为主导可变作用的标准值；γQj为第j个可变作用的分项系数；ψcj为第j个可变作用的组合系数；Qjk为第j个可变作用的标准值。

式中：ψfl为主导可变作用的频遇值系数，除有特别规定外，一般取1.0；ψqj为第j个可变作用的准永久值系数，除有特别规定外，一般取1.0。

考虑永久作用设计值与基本可变作用设计值，荷载组合为1.1自重+1.4结构附加重力+1.5列车活载，根据式（1）计算承载能力，结果见表2。计算应力、挠度和裂缝宽度时的荷载组合为1.0自重+1.0结构附加重力+1.0列车活载，与容许应力法采用的主力组合相同，参见表1。

表2 基于极限状态法不同列车活载组合的承载能力kN·m

按照Q/CR 9300—2018对桥梁的承载能力、应力、挠度和裂缝宽度进行检算。在承载能力检算中，T梁的材料参数见表3。

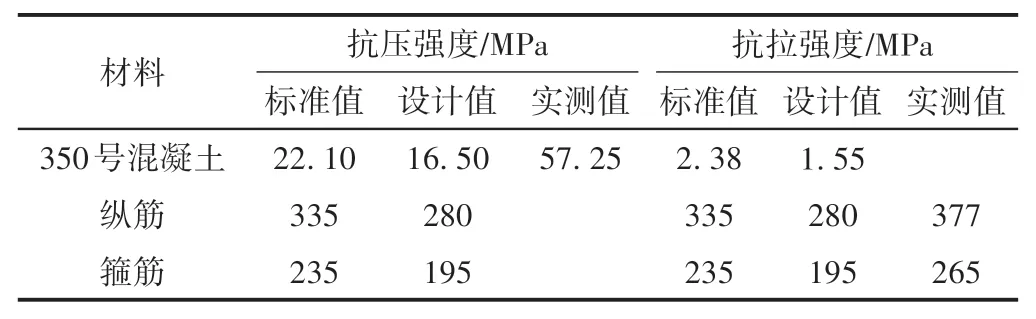
表3 材料参数

对于应力、挠度和裂缝宽度检算公式与容许应力法相同，荷载组合也相同，但是应力检算时钢筋应力的容许值［σs］=177.5 MPa，挠度的容许值［f］=l0/1 071。极限状态法计算结果见图3。

根据Q/CR 9300—2018承载能力计算公式和表3的材料参数，计算出T梁的抗弯承载力为4 010 kN·m，比容许应力法计算得到的抗弯承载力高60.7%，能满足轴重提升前后所有列车的承载能力要求。虽然极限状态法的挠度容许值（11 mm）比容许应力法的（15 mm）低25.3%，但列车静活载产生的挠度最大值为8.4 mm，仍小于极限状态法挠度限值。极限状态法的钢筋容许应力比容许应力法的小1.4%，在中—活载和恒载的荷载组合下，钢筋应力的计算值小于容许应力法的限值，但是采用极限状态法的设计理念会轻微超限。

图3 极限状态法计算结果

4 破坏试验

对钢筋混凝土T梁进行破坏试验得到实际承载能力，并与容许应力法和极限状态法两种设计理念得到的承载能力进行对比。

4.1 试验方案

基于两点加载弯曲试验开展T梁破坏试验和承载能力测试，加载位置见图4。因T梁承载能力较大，所以在现场设计拼装特殊加载反力架，在反力架和T梁之间设置液压千斤顶，同时在千斤顶和T梁之间安装压力传感器，控制和测量荷载。为了更真实地模拟T梁的实际受力情况，利用原桥拆下来的板式橡胶支座作为试验梁的支撑。

图4 加载位置（单位：mm）

4.2 加载过程

试验开始前需要先进行预加载，一方面消除T梁和设备之间的非弹性变形，另一方面检查加载装置及测试设备的可靠性和安全性。正式加载采用分级加载的方法，且用二期恒载和各列车活载作为控制荷载，加载过程分成两个加载阶段。第一加载阶段按照二期恒载、1.0倍二期恒载+1.0倍C64、1.0倍二期恒载+1.0倍C70、1.0倍二期恒载+1.0倍C80、1.0倍二期恒载+1.0倍中—活载、1.0倍二期恒载+1.0倍KM98的顺序进行加载，然后卸载。第二加载阶段重复第一加载阶段的六级加载，从第七级加载开始，后面在每个加载等级在前一级基础上增加0.5倍中—活载进行加载，直至梁体破坏。

4.3 测点布置

为了有效反映破坏试验中T梁的力学行为，在支座、1/4跨、1/2跨和3/4跨截面处布置挠度测点，在1/2跨截面处布置混凝土应变测点和钢筋应变测点，见图5。试验前首先对T梁表面进行打磨和清洁，然后在梁体左右两侧用白灰刷白，依次划上20 cm×40 cm网格用来观察裂缝发展的位置和程度。

图5 实际测点布置和现场照片（单位：mm）

4.4 试验结果及分析

4.4.1 挠度

极限状态法与容许应力法设计理念的挠度计算结果相同，统称为理论计算值。根据破坏试验得到跨中截面荷载-挠度曲线和列车静活载作用下的挠度，分别见图6、图7，荷载为四个千斤顶的荷载之和。由图6可知，荷载-挠度曲线分为三个阶段，分别是弹性阶段、带裂缝工作阶段和破坏阶段。荷载达到260 kN时曲线斜率发生变化，原因是T梁出现裂缝，梁体刚度减小；荷载达到1 800 kN时钢筋开始屈服，曲线斜率开始急剧变化；荷载达到2 120 kN时上缘混凝土被压碎，T梁破坏。由图7可知，破坏试验得到列车静活载下的挠度比容许应力法和极限状态法计算值平均低约8%，最大误差仅为10%，且均满足两种设计理念的容许值。

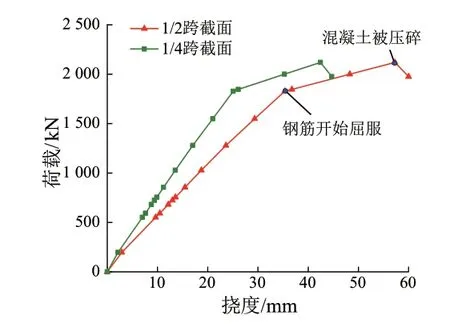
图6 跨中截面荷载-挠度曲线

图7 列车静活载下的挠度

4.4.2 应力

根据混凝土和钢筋应变的测试结果，得到破坏试验应力、应变曲线，分别见图8和图9。由图8可知，不同荷载组合下混凝土应力试验值比容许应力法和极限状态法的计算值平均小9.2%，钢筋应力平均小9.0%，且均符合两种设计理念的容许值。由图9可知，混凝土应变沿截面高度的变化基本符合平截面假定，与设计值相比中性轴发生了上移。在初始阶段钢筋的荷载应变曲线近似呈线性增长。当荷载到达1 800 kN，曲线有明显拐点，此时钢筋开始屈服。

图8 破坏试验应力

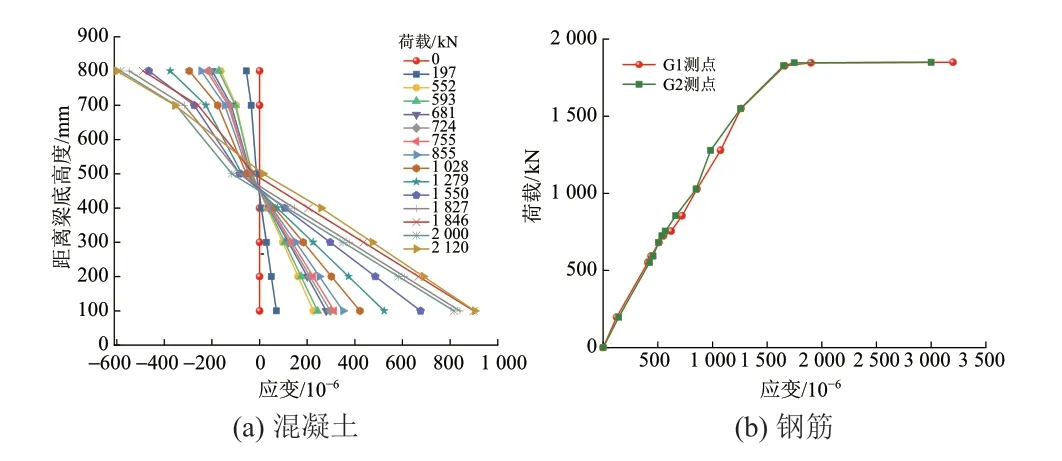
图9 破坏试验应变曲线

4.4.3 裂缝宽度

在破坏试验中，当荷载达到2 120 kN时，跨中位置底板及腹板裂缝宽度超过3.0 mm，顶板附近裂缝超过6.0 mm，梁体发生破坏。破坏形式是试验梁顶板混凝土压溃，而梁体破坏时底板钢筋屈服，底板箍筋外侧混凝土保护层脱落明显，跨中底板出现6条贯通裂缝，如图10（a）所示。不同列车活载组合下的试验裂缝宽度如图10（b）所示，与图2（c）对比可知，实际的裂缝宽度要比两种设计理念计算值平均大21%，但满足0.2 mm的限值。

图10 破坏试验裂缝情况及宽度

4.4.4 抗弯承载力

破坏试验和按照两种设计理念计算的承载能力见图11。其中，根据极限状态法计算得到正截面抗弯承载力为4 010 kN·m；破坏试验中，当加载荷载为2 120 kN时T梁受压区混凝土被压碎，梁体破坏，从而计算得到梁体实际抗弯承载力为6 362 kN·m，是根据极限状态法计算得到抗弯承载力的1.59倍，说明根据极限状态法设计桥梁具有较大的安全储备。在容许应力设计理念中并没有关于钢筋混凝土梁承载能力（即强度）计算的规定，但是根据混凝土应力、钢筋应力和裂缝宽度容许值可以反推出抗弯承载力，分别为2 496、2 772、3 410 kN·m。

图11 破坏试验承载能力

5 结论

1）对于铁路钢筋混凝土梁列车静活载下的挠度，两种设计理念中的计算公式和荷载组合均相同，破坏试验得到的挠度比两种设计理念计算值低约8%，满足挠度的容许值要求。

2）极限状态法与容许应力法设计理念中铁路钢筋混凝土梁的混凝土应力、钢筋应力的计算公式和荷载组合相同，混凝土和钢筋应力的理论计算值与试验值误差分别为9.2%和9.0%。而钢筋应力限值不同，造成在中—活载和恒载的荷载组合下，钢筋应力的计算值小于容许应力法的限值，但是在极限状态法的设计理念会轻微超限。

3）对于铁路钢筋混凝土梁裂缝宽度，两种设计理念中的计算公式、荷载组合和限值均相同，试验值比理论计算值高约21%，但满足两种设计理念要求限值。

4）对于铁路钢筋混凝土T梁，破坏试验得到的实际承载能力是根据极限状态法计算值的1.59倍，说明根据极限状态法设计铁路桥梁时有较大的安全储备。