L型分布式面阵二维高精度角度估计方法研究

李洪兵 欧阳婉 杨明磊 叶 舟 陈业伟 陈伯孝

(1.西北工业大学 西安 710072；2.西安电子科技大学雷达信号处理国家重点实验室西安 7100713；3.上海航天电子通讯设备研究所 上海 201109)

0 引言

米波雷达在反隐身和反辐射导弹等方面具有突出优势[1]，但波长限制了它的分辨力，大口径天线使雷达系统过于笨重，大大降低了其机动性，波束宽、角分辨率差等缺点也限制了其实现高精度目标定位与跟踪的能力。2006年林肯实验室提出分布式孔径相参合成雷达体制，提高雷达分辨力的同时也保证了其机动性[2]。阵列的分布式配置等效增大了阵列孔径，获得了较窄的主瓣，然而同时产生了大量幅度与主瓣接近的栅瓣，导致测角模糊，因此在分布式阵列测角中需要解决角度模糊问题。文献[3]基于双尺度旋转不变子空间算法(estimating signal parameter via rotational invariance techniques,ESPRIT)，分析了分布式阵列方向(Direction of arrival,DOA)估计的有效性与高精度性能，但是文中所提算法过程复杂，运算量大，难以应用于实际工程中的大型平面阵列。文献[4]基于分布式MIMO的DOA估计提出了一种实值处理算法，与传统的ESPRIT算法相比，减少了运算量，但是该算法需要解决优化问题，不满足工程应用实时性。

为提高米波雷达的角度估计性能，考虑实际工程应用的可行性，本文基于L型二维面阵分布式雷达，提出基于行列合成数据预处理的二维高精度角度估计方法。先通过数字加权对二维面阵做方位、俯仰维合成，分别合成为一维线阵，再分别使用双尺度酉ESPRIT[5]算法和合成导向矢量方法在方位维和俯仰维进行高精度角度估计，最后利用仿真实验验证本文算法的有效性和正确性。

1 阵列信号模型和算法描述

1.1 阵列模型

如图1所示，假设L型分布式面阵垂直放置，阵元分布在y-z平面上，由S1,S2,S3三个相同的平面天线子阵构成分布式相参阵列。每个平面子阵的天线在Y方向上有Ny个阵元，阵元间距为dy，两个子阵间距为Dy，在Z方向上有Nz个阵元，阵元间距为dz，两个子阵间距为Dz。

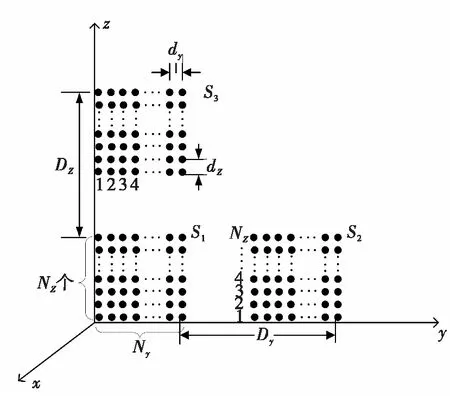
图1 L型二维面阵分布式相参阵列结构示意图

假设K个不相关的远场窄带信源入射到该分布式面阵上，设(φk,θk)为第k个信源的方位角与俯仰角，则y轴方向余弦为uk=cosθk·sinφk，z轴方向余弦为vk=sinθk，以子阵S1第一行第一个阵元为参考阵元，子阵S1的导向矢量矩阵可表示为

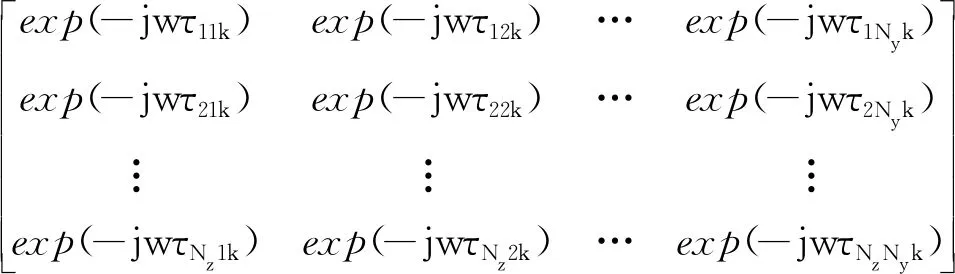
(1)

其中τmnk=exp(-j2π((m-1)dyuk+(n-1)dzvk)/λ)为第m行第n个阵元相对于参考阵元的延时。

子阵S2的导向矢量矩阵可表示为

A2k(uk,vk)=asub2A1(uk,vk)

(2)

其中asub2=exp(j2πDyuk/λ)为子阵S2相对于S1的相位中心的偏移量。

子阵S3的导向矢量矩阵可表示为

A3k(uk,vk)=asub3A1(uk,vk)

(3)

其中asub3=exp(j2πDzvk/λ)为子阵S3相对于S1的相位中心的偏移量。

1.2 算法流程

对时域采样的快拍数据首先分别沿行和列做数字波束形成(digital beam forming，DBF)，然后通过数字加权，等效得到两个一维线阵的接收数据矢量。然后在方位维上对波束合成后的线阵使用酉ESPRIT算法，再结合双尺度解模糊及自动配对算法[6]，实现方位维高精度角度估计。在俯仰维上低仰角和中高仰角情况采用不同算法，对于中高仰角情况，多径和直达波在角度维可以分开，用类似方位维角度估计方法进行处理。但对于低仰角情况，多径和直达波在角度维难以分开，上述方法不能准确估计俯仰角，因此需要针对低仰角情况下角度估计展开研究。利用雷达天线到目标的距离、镜像目标与真实目标间的几何关系等先验信息建立低仰角多径信号模型[3]。然后在俯仰维上对波束合成后的线阵采用基于合成导向矢量的超分辨算法[3]实现俯仰维高精度角度估计。因此二维高精度角度估计算法总体流程如图2所示。

图2 分布式面阵二维高精度角度估计算法总体流程图

下面分别详细介绍算法的原理及实现。

2 方位-俯仰维波束合成

如图1所示，分布式相参阵列包含S1,S2,S3三部雷达天线。估计方位角时，将S1和S2的数据先按列处理；估计俯仰角时，将S1和S3的数据按行处理，通过DBF将分布式相参阵列降维等效为方位维和俯仰维两个分布式一维线阵，如图3所示。

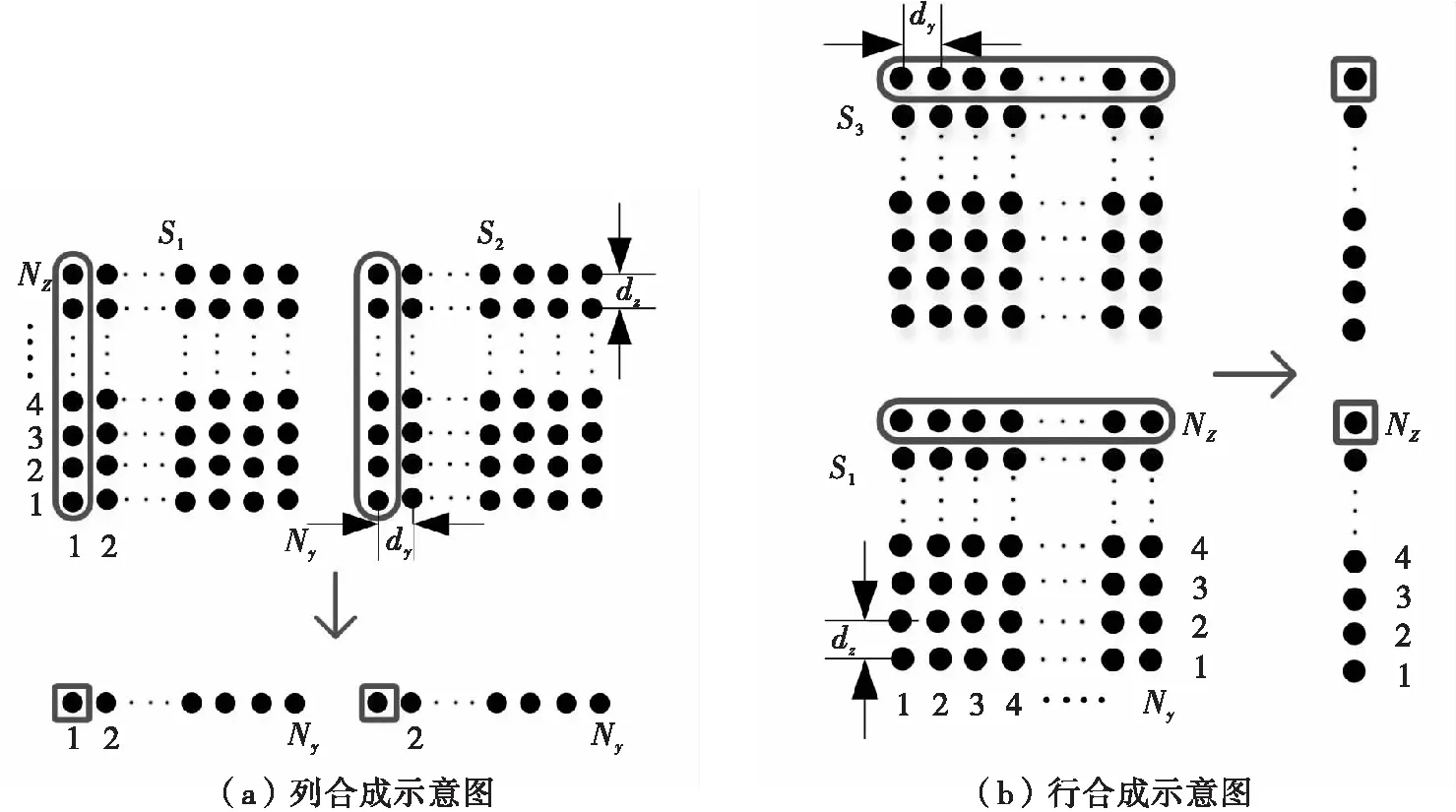
图3 二维面阵行列合成

在行列合成过程中，第k个信源子阵S1和子阵S2俯仰维加权矢量有

belk(vk)=[exp(-jwτ1k) exp(-jwτ2k) … exp(-jwτNzk)]

其中τnk=exp(j2π((n-1)dzvk)/λ)。子阵S1和子阵S3方位维加权矢量为

bazik(uk)=[exp(-jwτ1k) exp(-jwτ2k) … exp(-jwτNyk)]

其中τmk=exp(j2π((m-1)dyuk)/λ)。则方位维和俯仰维合成的等效合成信号可分别表示为

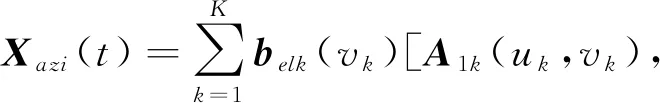
(4)

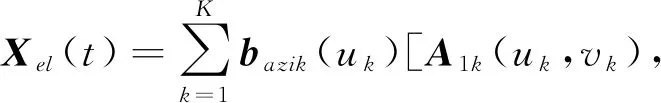
(5)

其中sk为第k个信源，n(t)为与信号独立的高斯白噪声构成的噪声矢量。

利用子阵S1和S2的列加权向量将面阵数据列合成为一行，利用子阵S1和S3的行加权向量将面阵数据行合成为一列。通过对各阵元数字化加权分别按行和列补齐相位，再对各子阵列通过数字加权求和，在方位维和俯仰维进行行列合成，得到方位维和俯仰维等效分布式线阵，可以增强信号能量，扩大天线孔径、提高角度分辨率和测角精度。

3 二维高精度角度估计

3.1 方位维高精度估计

分布式相参阵列会使其方向图主瓣变得窄，提升测角精度，但是也使得方向图出现大量幅度与主瓣相近的栅瓣，造成了分布式相参阵列的测角模糊问题。设单个子阵阵元数为20个，两个子阵间基线距离为30m，阵元间距取半波长时，可得阵列方向图如图4所示。其中，实线为分布式相参阵列的方向图，虚线为单个阵列的方向图。针对测角模糊问题，本文采用双尺度解模糊算法[6]来提高测角精度。

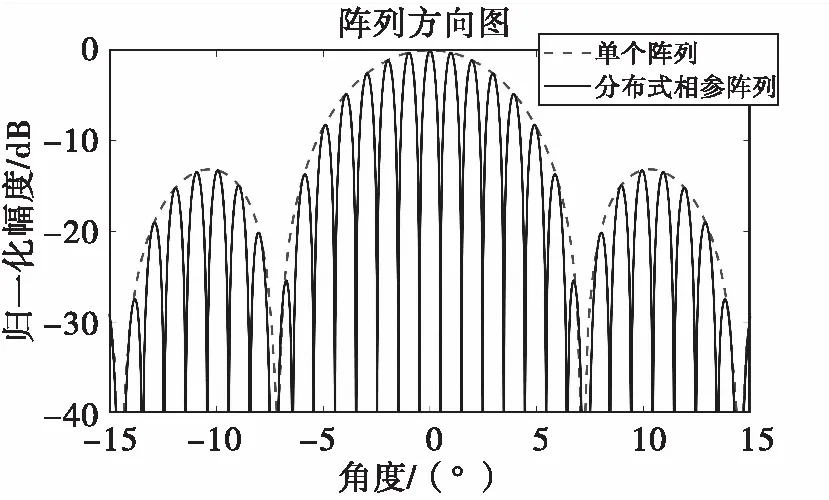
图4 分布式阵列和单个子阵方向图

1)信号模型

S1和S2列合成后的等效阵列如图5所示，可将其看成一维分布式阵列，它由两个基线距离为Dy的子阵组成，每个子阵内等间隔分布Ny个阵元，因此总阵元数N=2Ny，阵元间距为dy，子阵间距大于子阵孔径(Ny·dy)。

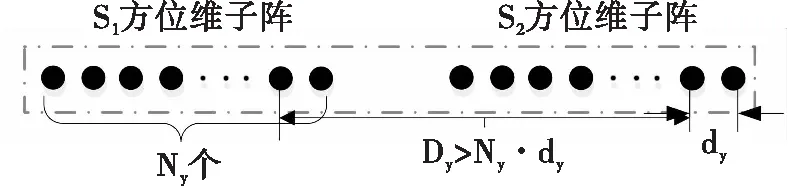
图5 方位维分布式阵列示意图

由第3节推导可知方位维等效信号为可表示为

Xazi(t)=AaziS(t)+N(t)

(6)

S(t)=[s1(t),s2(t)…sK(t)]T(上标T表示转置)为K个信源组成的信源矢量，N(t)=[n1(t),n2(t)…nK(t)]T为K个与信号独立的高斯白噪声构成的噪声矢量Aazi=[aazi1(u1),aazi2(u2),…,aaziK(uK)]为等效方位维阵列的导向矩阵，阵列的协方差矩阵为公式(7)。

(7)

其中，上标H表示共轭转置。

2)方向余弦的粗估计与精估计

对于方位维形成的分布式阵列，每个子阵内左侧的Ny-1个阵元与右侧的Ny-1个阵元具有偏移量为dy的平移不变性，同时两个子阵间具有偏移量为Dy的平移不变性。由偏移量大的平移不变性可得到精度高但周期模糊的方向余弦精估计，而偏移量小的平移不变性可得到精度低但无模糊的方向余弦粗估计，用粗估计对精估计解模糊便可得到高精度无模糊的角度估计值[7]。由ESPRIT算法可知，阵列偏移量为dy的旋转不变性[8]可描述为

(8)

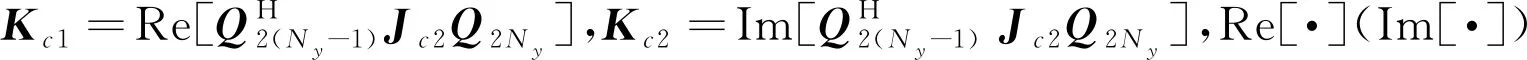
(9)

(10)

由于旋转矩阵为实值矩阵，因此可用自动配对算法实现方向余弦的粗估计与精估计配对，即Ψ=Ψc+jΨf从而得到正确配对的粗估计与精估计[6]。

(11)

其中γk为Ψ的特征值。

3)解模糊

分布式阵列的基线长度Dy远大于子阵孔径，方向余弦的精估计存在周期模糊，因此需要对精估计进行解模糊，利用双尺度解模糊法可以得到高精度无模糊的方向余弦估计uk为

(12)

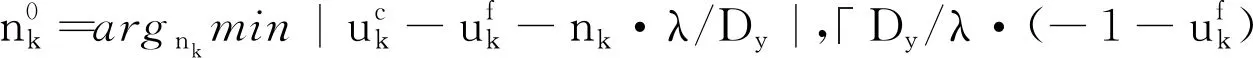
3.2 俯仰维高精度估计

如果目标信号在地面中高仰角处，多径和直达波在角度维可以分开时，可以用类似方位维的角度估计方法进行处理，由第3节推导可知俯仰维等效信号可表示为

Xel(t)=AelS(t)+N(t)

(13)

Ael为等效俯仰维阵列的导向矩阵，角度估计方法与方位维高精度估计相同。如果目标信号在地面低仰角区域，除了目标直达波，还要考虑信号经过多个传播路径的多径效应干扰，因此有必要针对低仰角条件下的分布式阵列俯仰维角度估计方法进行研究。

1)低仰角信号模型

俯仰维波束合成后的等效阵列如图6所示，可以看做在垂直维分布式布置的两个一维线阵，由子阵S1和S3的俯仰维组成，每个子阵由Nz个阵元等间隔分布，阵元间距为dz，子阵间距基线长度为Dz，分布式阵列天线相位中心高度为ha。

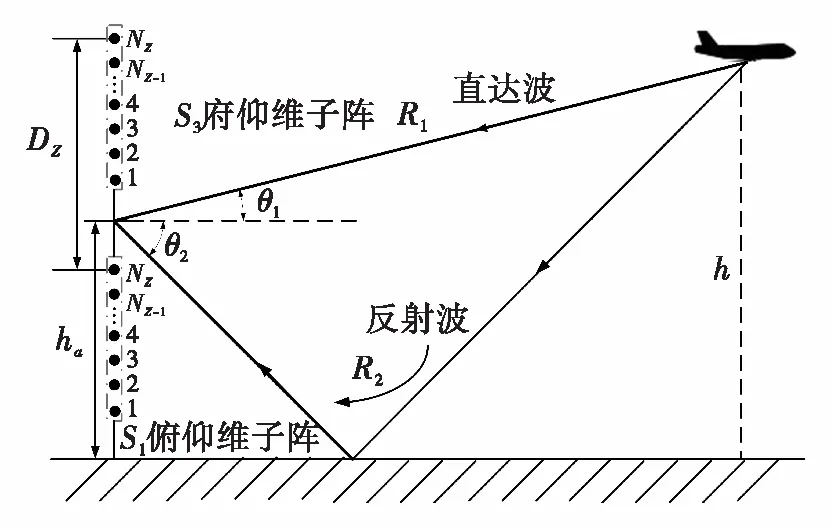
图6 分布式阵列俯仰维低仰角目标信号模型

目标直达波与镜像反射波的入射方向分别为θ1和θ2，两者波程分别为R1和R2，波程差ΔR=R2-R1。俯仰维直达波等效信号为Xel(t)，考虑地面反射波，多径信号可表示为

(14)

其中[a(θ1)a(θ2)]为分布式阵列的响应矢量；s(t)为直达信号复包络；ρ为地面反射系数。

2)基于合成导向矢量的超分辨算法

由于分布式阵列接收的回波信号中包括直达波和多径信号，因此将基于谱搜索的超分辨算法的导向矢量写为直达波和反射波两条路径的合成导向矢量形式[9]，得到的合成导向矢量为

A(θ)=A(θd)+ΓA(θs)

(15)

其中A(θd)=[a1(θ1),a2(θ1),…,aK(θ1)]为K个信源信号直达波的导向矢量，A(θs)为对应K个信源信号反射波的导向矢量，Γ为反射系数。利用合成导向矢量，通过最大似然(ML)算法[10]在仰角区间进行搜索，得到对应的目标仰角。对于ML算法，首先构成合成导向矢量的投影矩阵PML(θ)[11]为

PML(θ)=A(θ)[AH(θ)A(θ)]-1AH(θ)

(16)

然后，得到直达角的最大似然估计，R为信号的协方差矩阵[12]。

(17)

4 仿真结果分析

仿真时取如下参数：方位维单个子阵阵元数Ny=20；中仰角情况下阵列基线长度为30m；阵元间距dy=dz=0.3m；载波频率为580MHz；信噪比SNR定义为行列合成后单个等效阵元信噪比。

4.1 方位维测角结果

在以下方位维测角的仿真中，假设目标方位角为15°，快拍数L=16。

1)仿真1：分布式阵列方位角估计精度分析。

为对比分布式阵列和单个阵列方位角估计精度，取SNR=9dB，基线长度为30m时做500次Monte-Carlo实验结果如图7所示，从中可以看出分布式阵列比单个阵列的方位角估计精度更高，更稳定地趋近真实值。

图7 方位角估计结果对比

2)仿真2：方位角估计性能与信噪比的关系。

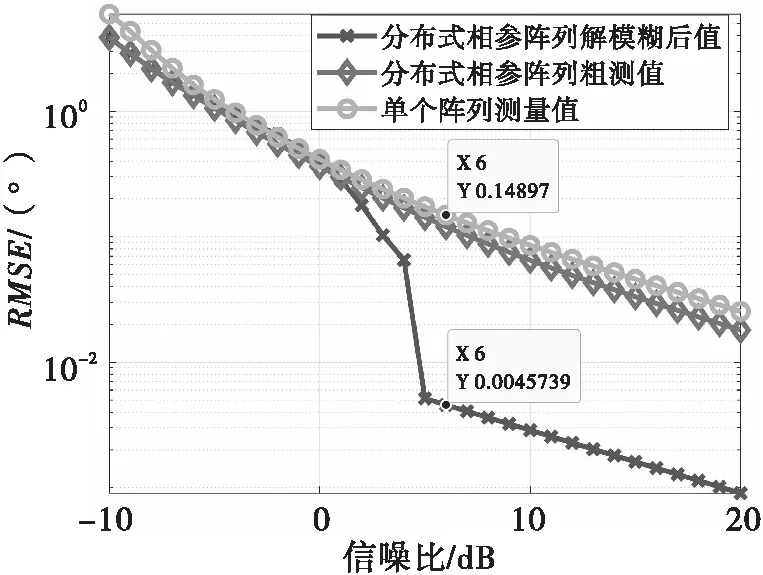
图8 方位角估计性能随SNR的变化情况

3)仿真3：方位角估计性能与基线长度的关系。

当两个子阵间间距越大，测角精度越高，但当基线大于某个值时，解模糊失败，估计性能迅速下降[15]。为分析分布式阵列和单个阵列方位角估计精度与基线长度的关系，取SNR=0dB时做500次Monte-Carlo实验结果如图9所示。从图中可以看出当基线长度大于57m时，分布式阵列解模糊后测角性能迅速变差，而分布式阵列粗估计和单个阵列估计则不受基线距离影响。当基线长度小于32m时，分布式阵列解模糊后均方根误差值随基线长度增大而减小。取基线距离为29.87m时，分布式阵列的测角均方根误差可以达到单个阵列的1/36。

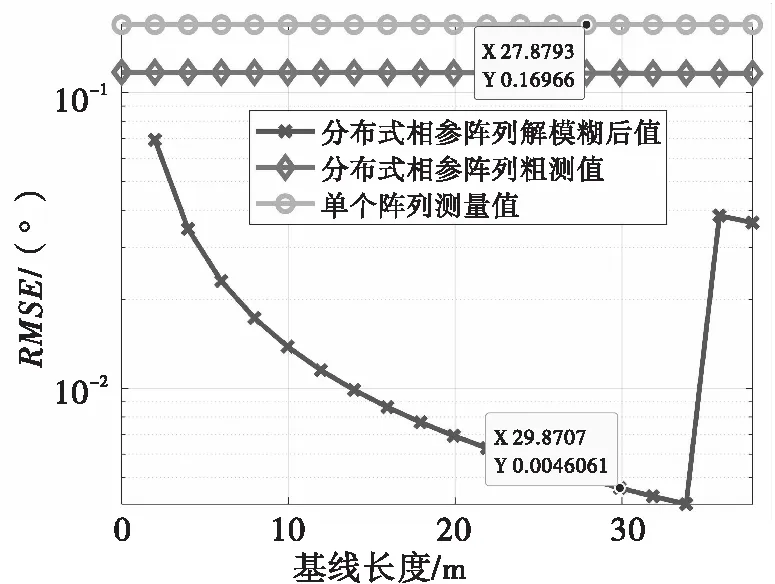
图9 方位角估计性能随方位维方向上基线长度的变化情况

4.2 俯仰维角度估计

俯仰维θ1选低仰角(3.44°)和高仰角(23.58°)两个目标，目标与天线参考单元的距离为R1为10km，目标的高度h=R1·sinθ1，分别为0.6km和4km，时域采样快拍数L=16。

1)仿真1：分布式阵列俯仰角估计精度分析。

为对比分布式阵列和单个阵列俯仰角估计精度，取信噪比为-3dB，基线长度为60m时做500次Monte-Carlo实验结果如图10所示，从中可以看出无论是在低仰角情况下还是在中仰角情况下，分布式阵列比单个阵列的方位角估计精度更高，更稳定地趋近真实值。

图10 分布式阵列和单个阵列俯仰维角度估计结果

2)仿真2：俯仰角估计性能与信噪比的关系。

由前文可知，角度估计中会出现SNR门限效应[13-14]。为分析分布式阵列和单个阵列俯仰角估计精度与信噪比的关系，低仰角和中仰角取基线长为62m(120倍波长)时做500次Monte-Carlo实验结果如图11所示，由图可知，随着信噪比的增长，角度估计的均方根误差逐渐变小。对比分布式阵列测量值与单个阵列测量值可知，取SNR=0dB时，不论是在低仰角还是中仰角情况下，分布式阵列的测角均方根误差可以达到单个阵列的1/10。

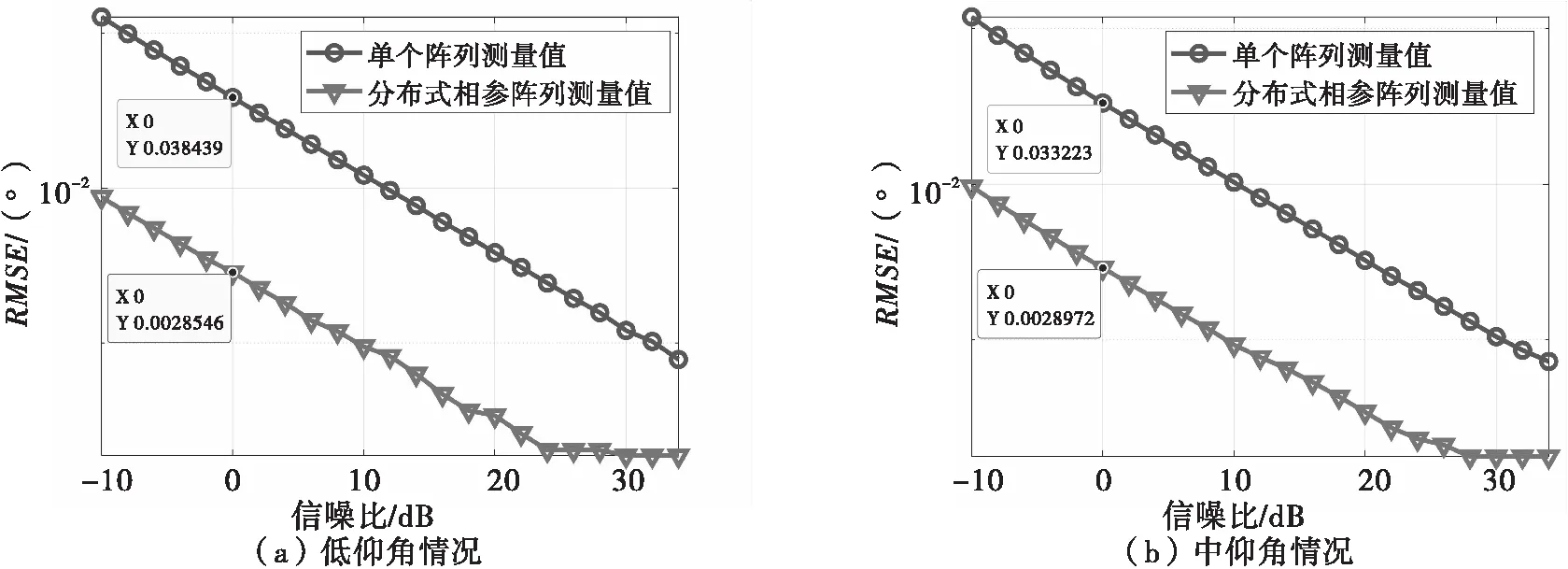
图11 分布式阵列和单个阵列俯仰维角度估计性能随信噪比的变化情况

3)仿真3：俯仰角估计性能与基线长度的关系。

由前文可知，角度估计会存在基线门限。为分析分布式阵列和单个阵列俯仰角估计精度与基线长度的关系，取SNR=-3dB时做500次Monte-Carlo实验结果如图12所示。从图中可以看出当基线长度分别大于101m和82m时，分布式阵列测角性能迅速变差。当基线长度小于基线门限时，分布式阵列均方根误差值随基线长度增大而减小。在低仰角情况和高仰角情况下，基线距离分别取66m和65m时，分布式阵列在俯仰维上的测角均方根误差可以达到单个阵列的1/10。

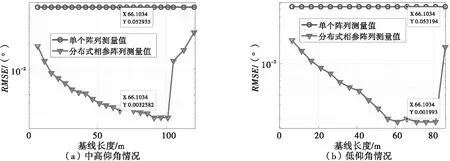
图12 分布式阵列和单个阵列俯仰维角度估计性能随基线长度的变化情况

5 结束语

针对米波雷达波束宽、测角精度低、硬件成本高及实现复杂度高等问题，本文提出一种L型二维面阵分布式雷达及其角度估计方法。在数字波束行列合成的基础上，将二维面阵合成等效为一维线阵，在方位维上运用双尺度酉ESPRIT算法，俯仰维低仰角条件下运用合成导向矢量算法进行二维高精度角度估计。仿真验证了分布式相参阵列相比于单个阵列大大提高了测角精度，同时也验证了分布式阵列的信噪比门限效应和基线门限效应。仿真结果证明了本文所提模型及其高精度角度估计算法的有效性，为实现高效的高精度角度估计打下了基础。