基于零陷展宽的米波雷达低仰角测高方法

王 梅 陈伯孝 徐赛琴 夏金艳

(1.西安电子科技大学雷达信号处理国家重点实验室 西安 710071；2.西安超视传感技术有限公司 西安 710065)

0 引言

米波雷达因其自身反隐身和抗反辐射导弹效能突出日渐受到了世界各国的高度重视，并广泛地应用于现代防控预警任务中，起到中远程警戒、目标跟踪及指示的作用[1]。然而米波雷达由于波束较宽，阵列孔径尺度有限，导致角度分辨能力较弱，特别是在低仰角目标探测时，由于同一个波束宽度内直达波和多径回波的共存现象，使得从时域、频域和空域对直达波和多径信号进行分辨较为困难，同时波束打地也会造成波瓣分裂[2-3]。因此，低仰角测高问题是米波雷达测高亟需攻克的难题之一。

目前，对于米波雷达测高技术，国内外已进行了大量研究并取得了丰富成果，主要常用的有以空间平滑(SpatialSmooth)为代表的多重信号分类算法(MultipleSignalClassification,MUSIC)[4]和以最大似然(MaximumLikelihood,ML)[5-6]为代表的参数估计类算法。空间平滑[7-8]的基本思想是将等距均匀线阵划分为若干个相互重叠的子阵，再对各子阵的协方差矩阵求平均以实现解相干，最后对MUSIC算法空间谱进行谱峰搜索得到波达方向(DirectionOfArrival，DOA)的估计值。ML算法[9]是一种白噪声情况下的贝叶斯最优估计，该算法利用阵列输出信号的统计分布特征，将数据协方差矩阵投影到期望的信号空间，实现目标仰角的最大似然估计，然而此类算法往往需要进行多维搜索，不利于实际工程实现，为此文献[10]提出了一种基于交替投影(AlternatingProjection,AP)的最大似然米波雷达低仰角测高算法，交替迭代优化直达波与多径回波角度，有效地解决了最大似然算法的多维搜索问题，并且降低了计算量。

然而上述测高算法均假设目标信号为远场点源，认为阵地反射面较为平坦，雷达接收的阵列回波信号中仅包含直达波信号和一路完全镜面反射后的多径反射波信号。实际阵地的反射面通常比较粗糙，多径信号复杂多变，雷达阵列接收的回波信号很难满足上述条件，阵列回波信号中除直达波信号外更包括非完全镜面反射后的多路多径反射波信号，这些信号通常集中分布在某个空域范围内，且空域间隔较小，此时的多径信号即应是分布源，因此建立基于复杂阵地的多径分布源模型[11-12]，提出一种基于零陷展宽低仰角测高算法，该算法首先将直达波与多径反射波视为干扰，然后采用投影变换和对角加载技术保留预设干扰区域扩展的协方差信号，减弱或消除其余非干扰信号存在对低仰角目标测角估计的不利影响，最后结合波束指向偏离搜索仰角的空域滤波器[13]得到在直达波入射方向具有一定深度的窄零陷和多径反射信号分布区内形成具有一定深度的宽零陷[14]，实现低仰角目标的DOA估计。相较于传统的米波雷达测高算法，本文提出的方法更适用于复杂阵地条件下的目标高度估计，且在低信噪比和少快拍数情况下依然能够保持较高的测角和测高精度。

1 信号模型

假设M个垂直放置且间隔为半波长均匀线阵，图1是在复杂阵地下低仰角测高的多径分布源模型几何表示(不考虑地球曲率)。其中hr表示天线中心架高；ht表示目标高度；Rd表示目标与雷达直达方向的距离；Rr=R1+R2表示多径反射距离；θd表示直达波方向的入射角；θr为多径反射分布区内的中心入射角；Δ为分布源参数。

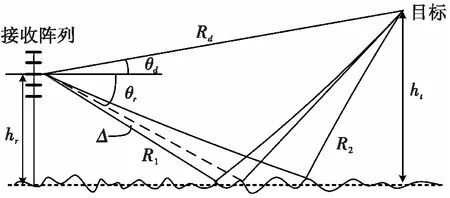
图1 复杂阵地下低仰角测高的多径分布源模型

设采样快拍数为N，则阵列回波信号矢量为

X(t)=[a(θd),a(θr,Δ)]ρs(t)+N(t),t=1,2,…,N

(1)

其中，a(θd)为直达波方向的导向矢量；a(θr,Δ)为多径反射分布区内的反射波导向矢量；ρ=[1,ρ0]T，ρ0为反射面反射系数，s(t)为信号复包络，N(t)为零均值的复高斯白噪声。式(1)中：

a(θd)=[a0(θd),a1(θd),…,aM-1(θd)]T
a(θr,Δ)=[a0(θr,Δ),a1(θr,Δ),…,aM-1(θr,Δ)]T

(2)

其中，上标T表示为矩阵的转置，am(θd)=exp(j2πmdsinθd/λ)，多径信号导向矢量am(θr,σ)为

(3)

其中，η(θ,θr,Δ)用来描述多条路径的分布情况，称为角分布函数，假设多径反射服从高斯分布源模型，则角分布函数为

(4)

将式(4)代入式(3)中，经过化简后得

(5)

令H(θr,Δ)=[h0(θr,Δ),…,hM-1(θr,Δ)]T，则a(θr,σ)可表示为

a(θr,Δ)=a(θr)⊙H(θr,Δ)

(6)

其中⊙表示Shur-Hadamard乘积，则式(1)可进一步表示为

X(t)=(A(θd)+ρ0A(θr)⊙H(θr,Δ))S(t)+N(t),t=0,1,…,N

(7)

对有限长接收数据，回波信号的协方差矩阵估计为

(8)

其中上标H表示共轭转置。当N>M时，矩阵RX正定。

2 零陷展宽算法

基于零陷展宽的低仰角目标估计算法，首先视直达波与反射波为干扰信号，利用投影变换和对角加载技术保留预设区域扩展的干扰信号，减弱或消去其它非干扰信号存在对目标仰角估计的不利影响，最后采用指向偏离搜索仰角的空域滤波器对阵列接收回波数据进行滤波处理，使得滤波后的波束只能在与直达波和多径回波干扰信号匹配的方向处形成零陷，而其它方向不受影响。因此，滤波输出信号功率最小时对应的正零陷角度即为目标直达波仰角的估计值。

2.1 投影变换

设θi为当前目标仰角，θj为多径反射分布区的中心入射角，在多径分布源模型中，多径反射波的中心会发生完全的镜面反射。因此，根据图1所示的几何关系有

θj=-arcsin(sinθi+2hr/Rd)

(9)

通过式(9)将θi和θj的空域二维角度搜索转化为一维角度搜索，从而有效地降低了计算量。

假设多路多径反射波集中地分布在Θ=[θj-Δ,θj+Δ]范围内，在此角度范围内等间隔的插入L个插值点，插值点处的导向矢量设为a(θj,l)，l=1,2,…,L，此时多径分布源模型的多径反射波导向矢量矩阵A(Θ)为

A(Θ)=[a(θj,1),a(θj,2),…,a(θj,L)]

(10)

构造干扰信号导向矢量协方差矩阵Ri为

Ri=a(θi)aH(θi)+A(Θ)AH(Θ)

(11)

对Ri进行特征分解，可以得到

(12)

其中，λk表示特征值；υk表示与特征值λk相对应的特征向量。

设一个给定的正常数ε，Ri特征分解后的前D个较大特征值满足下述关系：

(13)

由此可见，常数ε决定了所要选取的基向量个数，而前D个较大特征值对应的特征向量聚集了干扰信号协方差矩阵Ri中的大部分能量，有效地保留了预设区域扩展的干扰信号。前D个较大特征值对应的特征向量作为基向量张成的特征空间P1为

P1=span{υ1,υ2,…,υD}

(14)

根据特征向量生成投影算子，本文定义投影算子T为

(15)

T具有幂等特性，是一个投影矩阵。利用T对干扰信号导向矢量协方差矩阵Ri进行预处理，得到经投影变换后的协方差矩阵Ri-T为

Ri-T=TRiTH

(16)

从上述分析能够看到，投影变换T是通过Ri的特征分解运算得到，而Ri矩阵中既包含了直达波入射方位信息，同时也包含了Θ范围内的多路多径反射波的入射方位信息，因此起到了扩展多径方向零陷宽度的作用，Θ决定了零陷凹口的宽度。

2.2 对角加载

为提高波束形成器稳健性、降低副瓣电平，采用对角加载[15]方法对投影变换后的协方差矩阵Ri-T进行优化处理为

Ri-TD=Ri-T+λIM

(17)

其中，IM为M阶单位矩阵；λ为对角加载因子。

设空域滤波器的主瓣方向为θb，对应的导向矢量为a(θb)，为了使指向为θb的空域滤波器充分对消掉搜索仰角θi及对应的多径仰角范围Θ内的干扰信号，空域滤波器指向θb必须与搜索仰角θi保持一定的距离，即求解满足下述约束的自适应加权矢量W为

(18)

利用拉格朗日乘子法求解上述优化问题，得到滤波处理后的自适应最优加权矢量Wi为

(19)

使用式(19)得到的自适应最优权值向量Wi对阵列接收回波数据进行滤波处理，得到空域滤波后的输出信号功率为

（1）式中：D为缸径；α为热膨胀系数，合金铸铁α=1.2×10-5/℃；△t为活塞环与缸套的温差，气环为100℃，油环为80℃。

(20)

然后可计算如图1所示的基于多径分布源模型(不考虑地球曲率)下的目标高度ht为

(21)

值得注意的是，本文算法在空域滤波器指向θb的选取问题上要注意必须与搜索仰角θi保持恰适的距离，以保证较大的干噪比和良好的干扰对消效果，同时防止波束指向偏移和波束响应畸变。

低仰角测高问题暗含一个客观存在的先决条件就是目标仰角小于二分之一的俯仰维波束宽度，即3dB波束宽度的一半。根据理论分析和大量实测数据处理结果表明，当空域滤波器指向θb∈(θi/θ0,θi/θ0+θ3dB/2)时满足上述条件，θ3dB为3dB波束宽度，θ0为第一零点波束宽度。

3 计算机仿真

下面通过计算机仿真实验来验证本文算法的有效性。

仿真考虑一个由21个垂直阵元组成的半波长均匀线阵，天线架高15m，3dB波束宽度为4.83°。设目标距离为200km，高度5000m，直达波入射角为1.43°，多径信号服从高斯分布分布源模型，多径方向中心入射角为-1.44°，分布源参数Δ=0.6°，地面反射系数为-0.95。取快拍数为30，阵元信噪比为15dB。

仿真1：设基向量个数取3，对角加载因子λ为0.001，在上述仿真条件下，本文算法的空域滤波响应如图2所示。

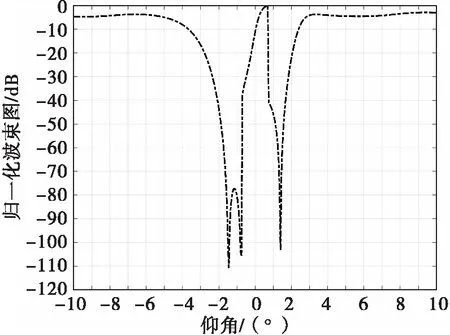
图2 本文算法空域滤波器响应

从图2可以看出，本文算法空域滤波后在直达波仰角1.43°附近处形成了具有一定深度的正零陷，在-1.5°至-1.38°角度范围内形成了具有一定展宽的负零陷，有效地抑制了入射角在此分布范围内的多径反射波信号，因此该算法可适用于复杂阵地环境下的目标仰角估计，其测角结果接近于真实值。

仿真2：基向量个数对本文算法空域滤波效果及测角性能的影响。取基向量个数D分别为1、2、3、4，对角加载因子λ为0.001，其余仿真条件不变，图3给出了本文算法在基向量个数不同情况下的空域滤波响应。

图3 基向量个数不同情况下的空域滤波器响应

从图3可以看出，基向量个数D不同，空域滤波效果会有明显差异。当基向量个数D取1时，多径方向的零陷深度较浅，零陷宽度也较窄，对复杂反射的多路多径反射波信号的抑制效果不佳，而直达波方向没有产生零陷，导致无法分辨直达波与反射波信号，本文算法测角性能失效。然而随着选取基向量个数D的增大，多径方向的零陷深度加深，零陷宽度也变宽，对复杂反射的多路多径反射波信号的抑制效果更加明显，而直达波方向的波束零陷虽然也不断加深，但是又存在零陷宽度变宽现象，这将导致阵列分辨率下降。因此，基向量个数D的选取需综合考虑多径抑制效果和阵列分辨率。

仿真3：对角加载因子对本文算法本文算法空域滤波效果及测角性能的影响。取基向量个数为3，设置对角加载因子λ分别为0.01、0.001、0.0001、0.00001，其余仿真条件不变，图4给出了本文算法在不同对角加载因子情况下的空域滤波响应。

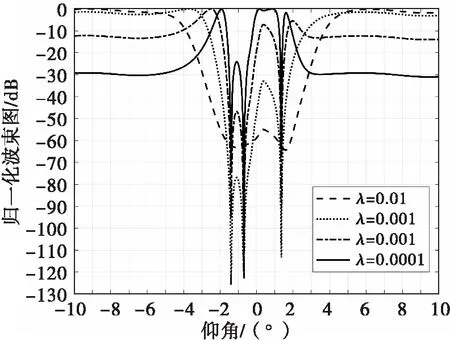
图4 不同对角加载因子情况下的空域滤波响应

从图4中可以看出，对角加载因子λ的取值对空域滤波效果也会有一定影响。当λ取一个较大值0.01时，零陷深度比λ取 0.001时的零陷深度要浅，多径方向干扰的抑制效能和阵列分辨性能均下降；当λ取一个较小值0.00001时，多径反射分布区和直达方向处的零陷深度均比λ取 0.0001时的零陷深度要浅。综上考虑，本文算法对角加载因子λ当取在0.00001 ≤λ≤0.01范围内，都会有良好的空域滤波效果并且实现阵列的有效分辨。

仿真4：信噪比对各算法测角性能的影响。取基向量个数为3，对角加载因子λ为0.001，阵元信噪比从0dB至20dB变化，其余仿真条件不变。比较本文算法与传统超分辨算法SSMUSIC及APML算法在不同信噪比条件下进行200次蒙特卡洛实验的测角结果。图5给出了不同算法测角均方根误差随信噪比变化的关系曲线。

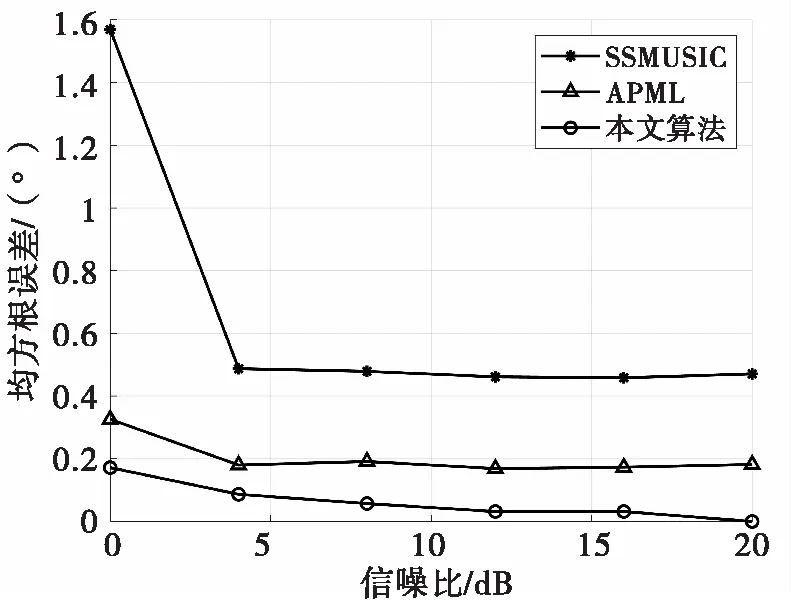
图5 测角均方根误差随信噪比变化

从图5可以看出，三种算法的测角均方根误差均随着信噪比的增大而减小，并且在信噪比变化范围内，SSMUSIC算法的测角均方根误差最高，APML算法次之，而本文所提算法的测角均方根误差最小，测角性能稳定。这是由于在复杂阵地环境下传统的超分辨算法SSMUSIC 和APML回波模型严重失配，无法准确分辨直达波和多径反射波信号，导致测角和测高误差较大，而本文算法建立在复杂反射多径的分布源模型上，通过空域滤波在多路多径反射波入射区域范围内形成一条具有一定深度的宽零陷，降低了复杂多变的多径信号对测角性能带来的影响，从而提高了测角精度。

仿真5：快拍数对各算法测角性能的影响。取基向量个数为3，对角加载因子λ为0.001，快拍数从5至50变化，其余仿真条件不变。比较本文算法与传统超分辨算法SSMUSIC及APML算法在不同快拍数条件下进行200次蒙特卡洛实验的测角结果。图6给出了不同算法测角均方根误差随快拍数变化的关系曲线。

图6 测角均方根误差随快拍数变化

从图6可看出，随着采样快拍数的增大，各算法的测角均方根误差逐渐减小，其中本文所提算法的测角均方根误差小于传统超分辨算法 SSMUSIC和APML，具有较高的测角精度，验证了本文算法的有效性。

4 结束语

复杂阵地环境下粗糙反射面引起的多径信号呈现多路分布，为此提出一种基于零陷展宽的低仰角测高方法。该方法将直达波和多径回波当作干扰处理，利用指向偏离目标仰角的空域滤波器，再结合投影变换和对角加载技术对阵列回波信号进行滤波处理，抑制了复杂多变的多路多径反射波信号对测角性能的影响，从而提高测角和测高精度。与传统超分辨测高算法相比，本文所提算法易于求解，更适用于复杂阵地环境下的目标高度估计，并且在低信噪比和少快拍数条件下仍具有较高的测角和测高精度。