波动工况下点焊质量在线预测及模型解释

2023-01-08吕天乐齐苗苗闫德俊黎书华夏裕俊李永兵

焊接学报 2022年11期

吕天乐，齐苗苗，闫德俊，黎书华，夏裕俊，李永兵

(1.上海交通大学,上海市复杂薄板结构数字化制造重点实验室,上海,200240；2.上海交通大学,机械系统与振动国家重点实验室,上海,200240；3.上海航天设备制造总厂有限公司,上海,200245；4.中船黄埔文冲船舶有限公司,广东省舰船先进焊接技术企业重点实验室,广州,510715)

0 序言

由于成本低、效率高、易自动化，电阻点焊技术成为薄壁结构制造的主要连接工艺.以汽车制造为例，一辆钢制轿车车身通常有3 000～ 7 000 个焊点，占其焊接总量的80%以上[1]，因此，焊点质量直接决定着车身的使用寿命和安全性.出于车身减重和节能减排的需要，轻质高强材料已得到广泛应用.但是，高强材料冲压后大回弹带来的装配偏差，会导致板间间隙、电极工件不垂直、边缘焊等异常工况波动，改变焊点接触状态并引发虚焊、飞溅等一系列焊接质量问题，影响焊点质量一致性[2].为此，亟需实现焊点质量在线检测与实时控制，保障产品可靠性.

目前，国内外学者已基于焊接过程多传感信号的点焊质量在线检测技术方面开展了大量研究.其中，动态电阻、电极位移和电极力是最常用的表征熔核生长过程的传感信号[3-4].Dickinson 等人[5]发现动态电阻信号可以有效反映点焊熔核在焊接各阶段的形成和生长过程；Chang 等人[6]则证明焊接工件受热膨胀导致的电极位移信号与熔核生长具有更强关联性，但由于位移量级较小，测量存在一定难度；电极力也受工件膨胀影响，且测量方便、不易干涉焊接过程，Zhang 等人[7]认为电极力可以替代位移信号.

机器学习模型被用于建立过程信号与关键质量指标的关联关系.Chen 等人[8]使用主成分分析对过程信号特征进行降维，发现板材种类显著影响特征分布，因此使用k 均值聚类对数据集进行预分类，再训练反向传播(BP)神经网络模型，预测精度提高.Gavidel 等人[9]对比了人工神经网络、回归树、k 近邻、深度神经网络、随机森林、支持向量机等常用模型在点焊数据集上的性能，发现深度神经网络的预测精度和稳健性最高.Zhao 等人[10]使用不同的数据降维方法提取动态电阻信号特征，预测模型得到比人工特征更好的性能.El-Sari 等人[11]发现仅基于工艺参数训练的多层感知机回归模型对不同板材数据集的泛化性很差，而引入电阻信号训练的模型，其外推能力明显改善.Zhou 等人[12]研究了数据量和信号特征种类对回归模型性能的影响，认为超过250 组数据、电信号特征输入即可获得较好预测效果.基于过程信号的机器学习模型可以较为准确地预测焊点质量，但现有研究主要面向待焊工件处于理想匹配状态的情况，对异常工况波动的研究较少，其分析结果可能不具有较好的代表性.

文中围绕工况波动问题，通过试验获得包含四种焊接工况下焊点质量与动态电阻、电极力、位移信号的数据集，分析了焊点质量在波动工况下的分布差异并提取过程信号特征，对比了多元线性回归、高斯过程回归、支持向量回归、神经网络等机器学习模型在波动工况数据集上的预测性能，并研究了输入特征量、信号和工况波动对模型性能的影响.

1 试验数据集创建

1.1 试验设备

试验使用的电阻点焊设备平台由FANUC R2000iB 电阻点焊机器人、OBARA C 型焊枪和中频直流(MFDC)控制器组成.电极选用端面直径为6 mm 的CuZr 电极，冷却水流量为11.3 L/min.

焊接监测平台使用固定在静电极杆上的罗氏线圈(精度为0.5 %)测量次级电流，使用上下电极上安装的屏蔽双绞线测量电压，利用欧姆定律计算得到动态电阻信号.通过安装在静电极臂上的表面应变片传感器(精度为2 %)测量电极力，并根据力计算静电极位移；动电极位移由安装在动电极导轨顶端的旋转编码器(分辨率为0.5 μm)测量，两者之和为总电极位移.具体测量方法和信号计算公式见文献[13].

1.2 焊接条件与工艺参数

待焊工件选用汽车行业常用的两种钢材：双相高强钢DP590 和冷轧钢BUFD，表面无涂层，板厚为0.8 mm 和1.6 mm.两种材料的化学成分和力学性能见表1 和表2.

表1 DP590 和BUFD 的化学成分(质量分数, %)Table 1 The chemical components of DP590 and BUFD

表2 DP590 和BUFD 的力学性能Table 2 The mechanical properties of DP590 and BUFD

为研究波动工况对焊点质量及焊接过程的影响，试验中设计了四种不同的电极与工件匹配状态，用以模拟实际生产中零件装配偏差导致的焊接工况波动，即：标准工况、倾斜工况、边距工况和间隙工况.相关试样尺寸和试验设置方法如图1 所示.

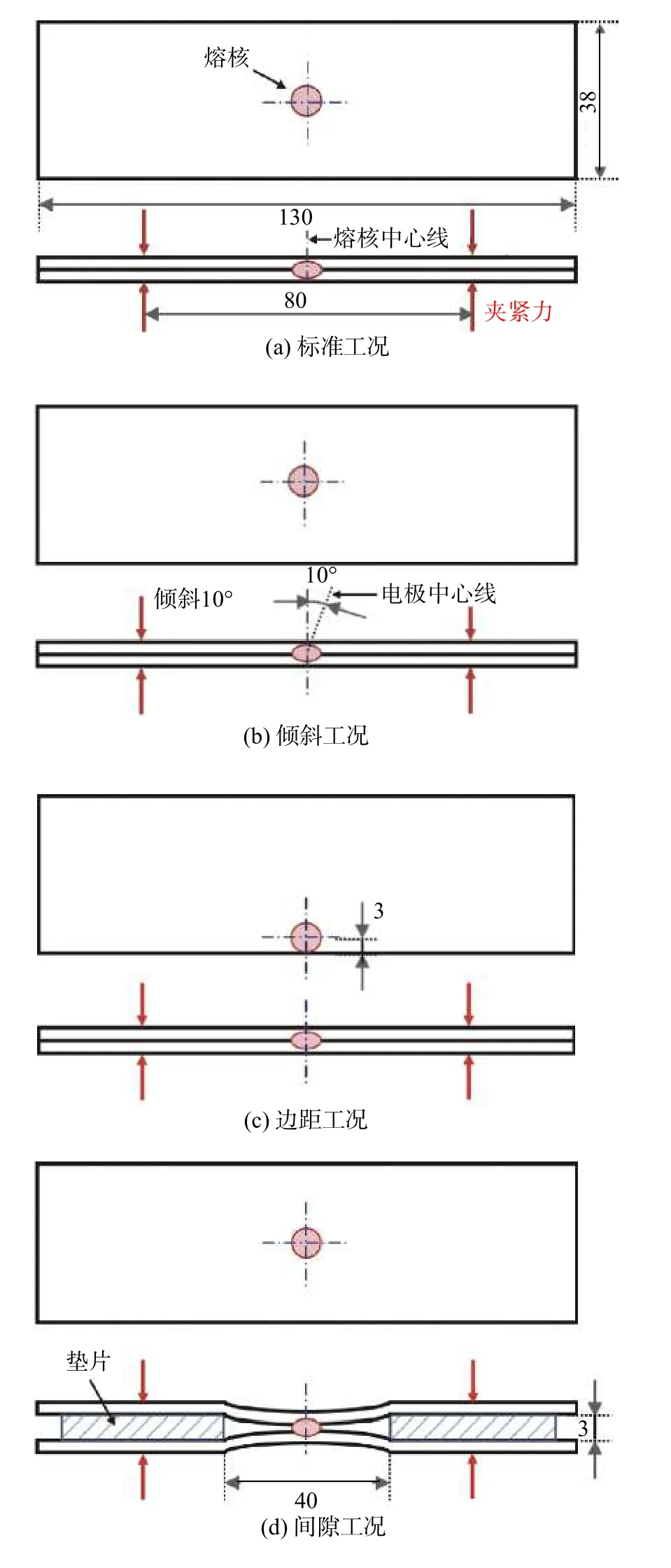
图1 标准、倾斜、边距和间隙工况的试样尺寸及设置方法示意图(mm)Fig. 1 Schematics of the specimens and setup methods of standard, electrode angle, edge proximity and initial gap conditions (mm). (a) standard condition; (b) electrode angle condition; (c) edge proximity condition; (d) initial gap condition

将待焊工件按照等强等厚、等强差厚、等厚差强和差强差厚四种方式搭配成不同的板材组合，选用单脉冲恒流焊接规范，采用不同的焊接电流、电极力和焊接时间进行焊接试验.焊接方案设计见表3.焊接后，使用剥离熔核直径作为焊点质量的评价指标，测量每组试验中剥离熔核的最大和最小直径，取平均值作为最终的熔核直径[14].

表3 焊接方案设计Table 3 Welding schedule design.

1.3 焊接数据集

文中总计进行了300 组试验，各板材组合均有75 组.各组试验均记录了焊接工艺参数以及焊接过程中的动态电阻、电极力、位移信号.试验测得的剥离熔核直径的数据分布如图2 和图3 所示，总体数据分布具有典型的正态分布趋势，减少了板材匹配变化对数据分布的影响，平均熔核直径为4.44 mm；工况波动对熔核直径分布有一定影响，相比于标准工况结果，倾斜和边距工况下熔核直径较小，边距和间隙工况下熔核直径分布较集中.

图2 不同板材组合的熔核直径Fig. 2 Nugget diameter of different stack-ups

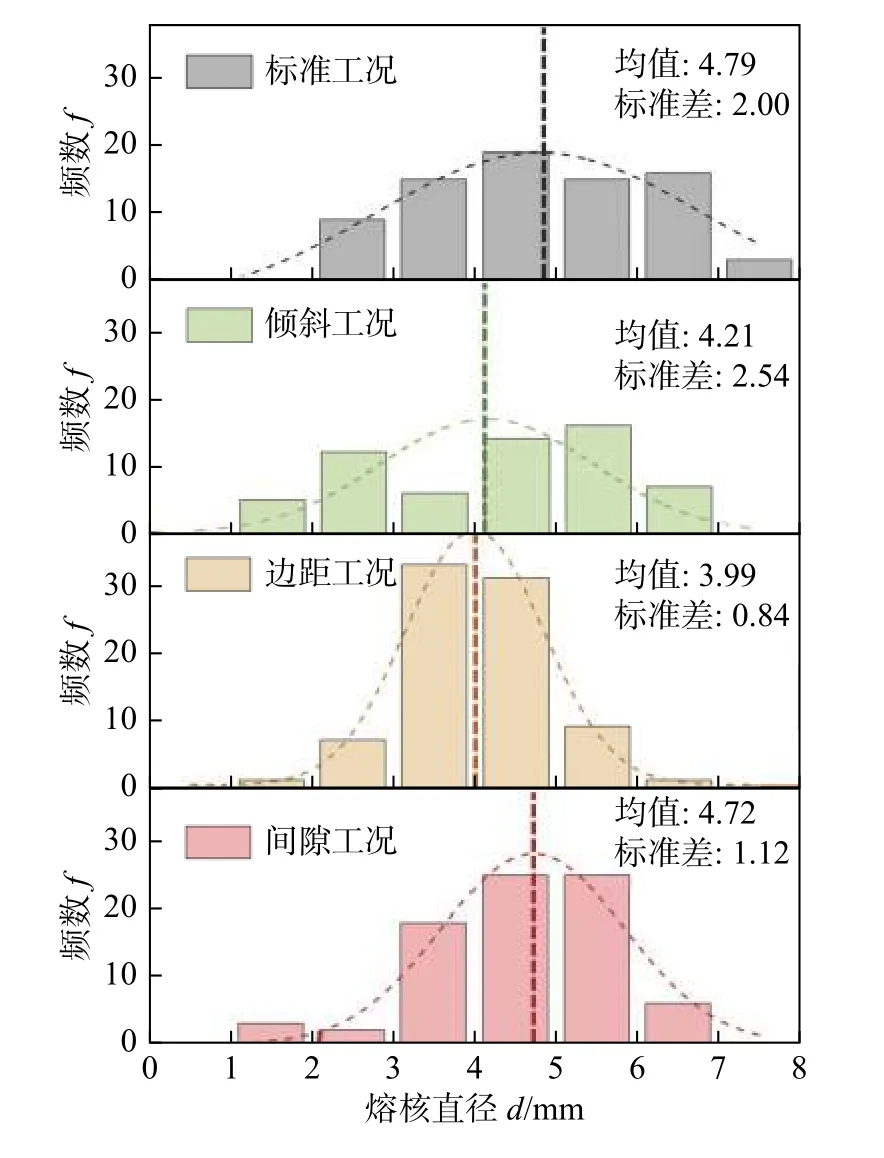
图3 不同工况的熔核直径Fig. 3 Nugget diameter of different conditions

2 不同机器学习回归模型对比

2.1 回归预测建模流程

文中基于焊接试验工艺参数和焊接过程信号特征，建立了熔核直径的回归预测模型.回归预测建模流程图如图4 所示.首先，提取过程信号特征并进行0-1 标准化处理，将其作为输入特征代入四类机器学习模型；随后，以模型的输出变量为熔核直径预测值，与实测熔核直径进行比较，从而对机器学习模型进行参数优化；最后基于熔核直径的预测性能挑选性能最优的机器学习模型.

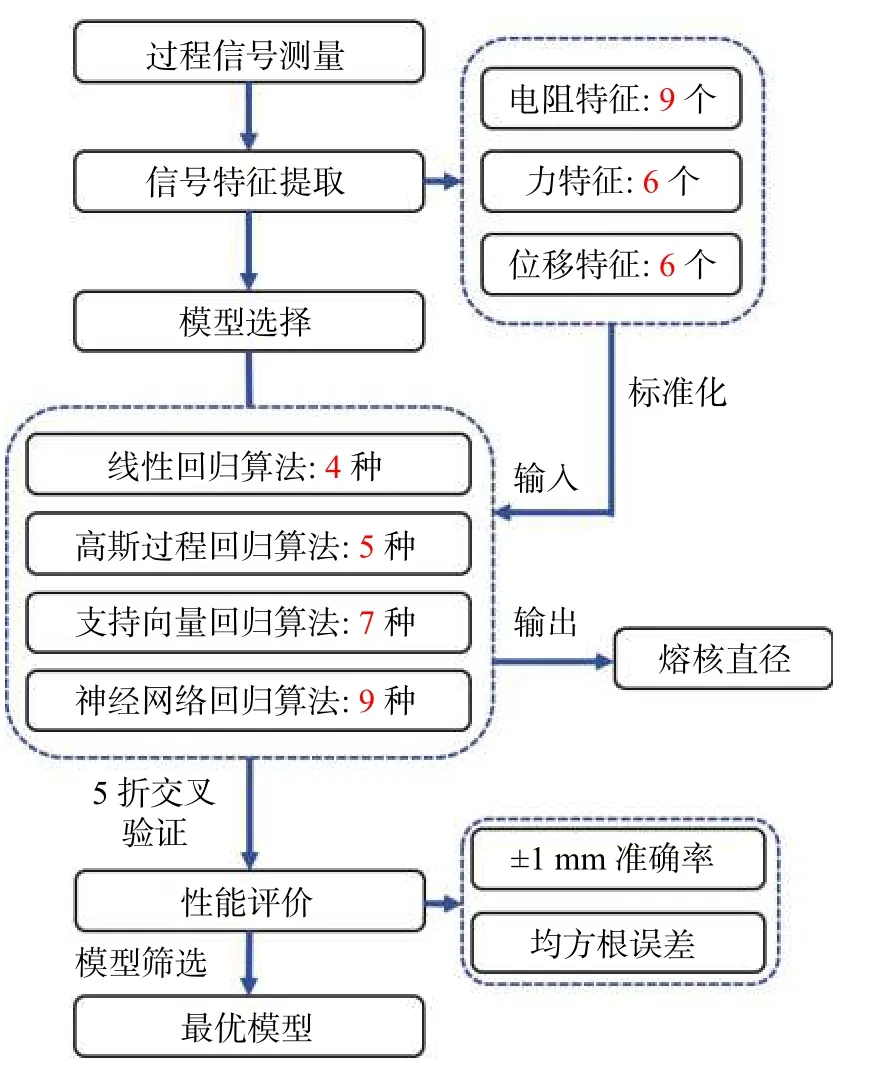
图4 回归预测建模流程图Fig. 4 Flowchart of regression prediction modeling

输入特征共有26 个，其中，焊接工艺参数共5 个，分别记为总板厚Thk_t、主导板厚Thk_g、设置电极力SetF、焊接电流SetI和焊接时间SetT，实际生产中无法获得焊接工况类型，因此不将预设工况作为特征值.过程信号的特征共21 个，其提取方法如图5 所示.其中，电阻特征共9 个，分别为热输入能量E、均值电阻Rav、谷值电阻Rmin、谷值电阻时刻trmin、峰值电阻Rmax、峰值电阻时刻trmax、终值电阻Rend、终值电阻时刻trend和电阻下降量Rdrop；力特征共6 个，分别为均值力Fav、峰值力Fmax、峰值力时刻tfmax、终值力Fend、终值力时刻tfend和力下降量Fdrop；位移特征共6 个，分别为位移平均值Sav、峰值位移Smax、峰值位移时刻tsmax、位移终值Send、位移终值时刻tsend和位移下降量Sdrop[15].

图5 过程信号特征提取示意图Fig. 5 Schematics of feature extraction methods of dynamic resistance, electrode force and electrode displacement signals. (a) dynamic resistance features; (b)electrode force features;(c) electrode displacement features

机器学习模型选用多元线性回归、高斯过程回归、支持向量回归和神经网络回归模型，以焊接工艺参数和过程特征作为输入的预测特征量，以熔核直径为预测目标，并在训练中对各模型的主要超参数进行优化，同时采用5 折交叉验证方法减少预测模型过拟合倾向.预测模型的性能评价指标有2 个，均为5 折交叉验证中测试集的测试结果.其中，第一个指标为预测值与实测值的均方根误差(RMSE)，计算公式为

式中，N为训练集样本总数量；Xpred为预测熔核直径；Xexp为实测熔核直径.

第二个指标是直径预测误差小于 ± 1 mm 的数据数量相对于总预测值数量的比例(记为A±1mm)，计算公式为

2.2 多元线性回归模型

文中对比了四种多元线性回归模型(记为MLR)的预测性能，包括标准MLR、含交互项MLR、稳健性MRL 和逐步MLR，并对输入特征量、拟合方法和输入项数量的优化，结果见表4.含交互项MLR模型的性能最差，A±1mm仅有11.75%，其它三种模型性能较好，预测精度均超过85%.其中，逐步MLR模型的性能最好，A±1mm接近90%，均方根误差仅有0.665 mm，其次为标准MLR 和稳健性MLR.

表4 线性回归模型的预测性能对比Table 4 Performance comparison of multiple linear regression models.

2.3 高斯过程回归模型

文中对比了使用不同核函数的高斯过程回归模型(记为GPR)的预测性能，包括二次有理函数、指数函数、平方指数函数，并使用贝叶斯优化器对所有超参数进行探索寻优，结果见表5.四种GPR模型均获得了较好的预测性能，A±1mm均超过90%.其中，指数核函数获得了最佳性能，A±1mm达到91.12%，其它超参数优化后的可优化GPR 的预测性能也未出现明显提升.

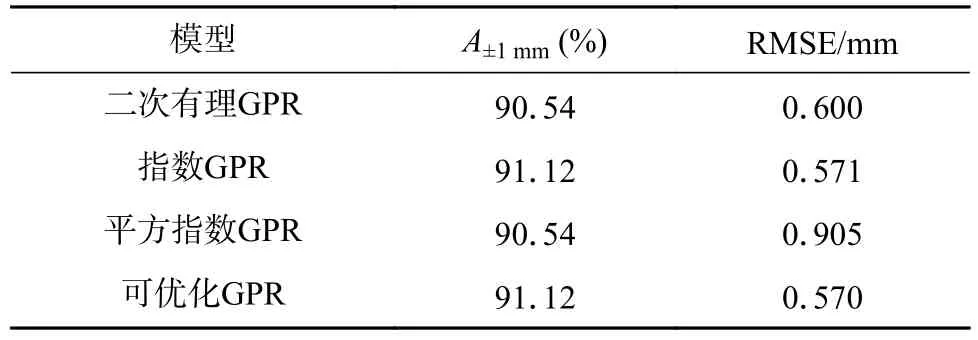
表5 高斯过程回归模型的预测性能对比Table 5 Performance comparison of Gaussian process regression models.

2.4 支持向量回归模型

文中对比了具有不同尺度的线性核函数、多项式核函数以及高斯核函数的支持向量回归模型(记为SVR)的预测性能，并使用贝叶斯优化器对超参数进行优化，各模型的性能见表6，其中多项式核的阶数分别为2 和3，高斯核中设置了三种水平的核尺度，混合核为线性核、多项式核以及高斯核的线性组合，优化后各项核的权重依此为0.90、0.05、0.05.SVR 模型具有较好的预测性能，A±1mm普遍获超过80%.其中，中等高斯SVR 模型获得最高精度和最低均方根误差，因此最优.对SVR 进行超参数优化以及混合核函数各项的权重优化未能进一步提升预测性能.

表6 支持向量回归模型的预测性能对比Table 6 Performance comparison of support vector regression models.

2.5 神经网络回归模型

文中对比了具有不同网络结构的全连接神经网络模型(记为MLP)的预测性能，网络均使用ReLU 激活函数，其结果见表7.可以看出，增加网络层数和每层节点数可以提升A±1mm和降低RMSE，但效果有限.所有神经网络模型的精度均在80%左右，三层神经网络的精度可以超过85%，每层500 个节点数的三层神经网络获得了最高的预测精度，A±1mm达到88.25%，但当节点数继续增加，A±1mm开始下降，仅通过增加节点无法继续提升精度.使用残差网络结构(ResNet)降低层数增加产生的退化问题，为保证足够的网络复杂度，在MLP 中叠加50 个残差结构(记为ResNet-MLP)，总层数为254，但在相同节点数下，预测精度均明显低于MLP，不能满足预测需求.

表7 神经网络回归模型的预测性能对比Table 7 Performance comparison of multilayer perceptron regression models.

2.6 不同模型的性能对比

在四种机器学习回归模型中，高斯过程回归模型获得的性能最好，A±1mm超过90%，其次是多元线性回归和支持向量回归模型，神经网络回归模型性能最差.其中，逐步线性回归、可优化高斯过程回归、中等高斯支持向量回归和三层500 节点神经网络分别是各模型中性能最好的模型.

为了更准确地评价这四种模型的性能，对其进行了10 次重复测试，对比平均性能及性能波动情况，其结果见表8.结果进一步证明了GPR 模型具有最佳和最稳定的预测性能，A±1mm和RMSE 均有较好的可重复性，前者波动小于0.5%，后者小于5%；SVR 模型具有次高精度，性能波动略大；而MLR 和MLP 模型的精度和波动均较差.

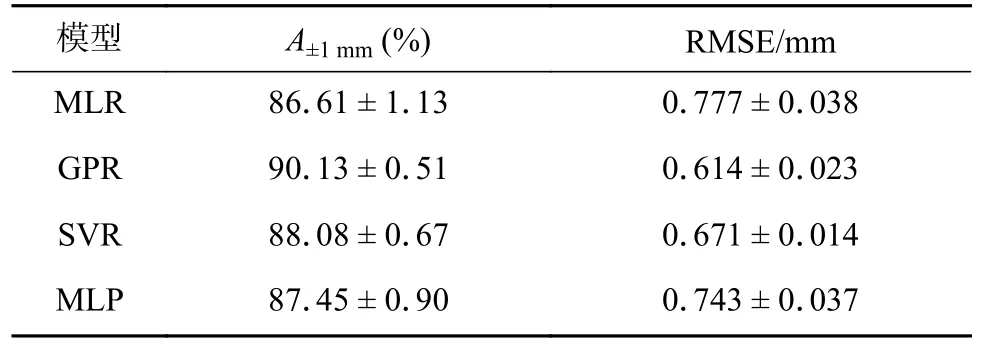
表8 优化后回归模型的预测性能及稳定性Table 8 Prediction performance and stability of optimized regression models.

各已优化模型的预测—实测值的结果如图6所示.MLR 和MLP 模型的预测结果分布范围较大，虽然大部分在误差许可范围内，但存在部分预测点位于距允许范围较远处，导致其精度及均方根误差波动较大；而GPR 和SVR 模型的预测结果分布较为密集，大部分预测数据点集中在准确预测线附近，超出允许范围的点也很接近误差允许界线，因此在保证较高的预测精度的同时，其性能稳定性也较好.因此，下一节将针对性能最佳的GPR 模型开展进一步研究.

图6 不同机器学习回归模型的预测—实测值Fig. 6 Prediction-response results of different machine learning regression models. (a) multiple linear regression;(b) Gaussian process regression; (c) support vector regression; (d) multilayer perceptron regression

3 波动工况下的模型性能解释

3.1 输入特征的重要性分析

为定量解释所选输入特征量的重要程度以及对异常工况波动的适应性，分别针对仅含标准工况的试验数据集(记为ST)和含异常工况的完整数据集(记为ALL)训练GPR 模型，并使用Shapley加和解释(SHAP)方法对26 个输入特征量进行分析，以衡量其对熔核直径预测值的贡献.对GPR 模型预测值贡献较大的前20 个特征量的Shapley 值分布如图7 所示.

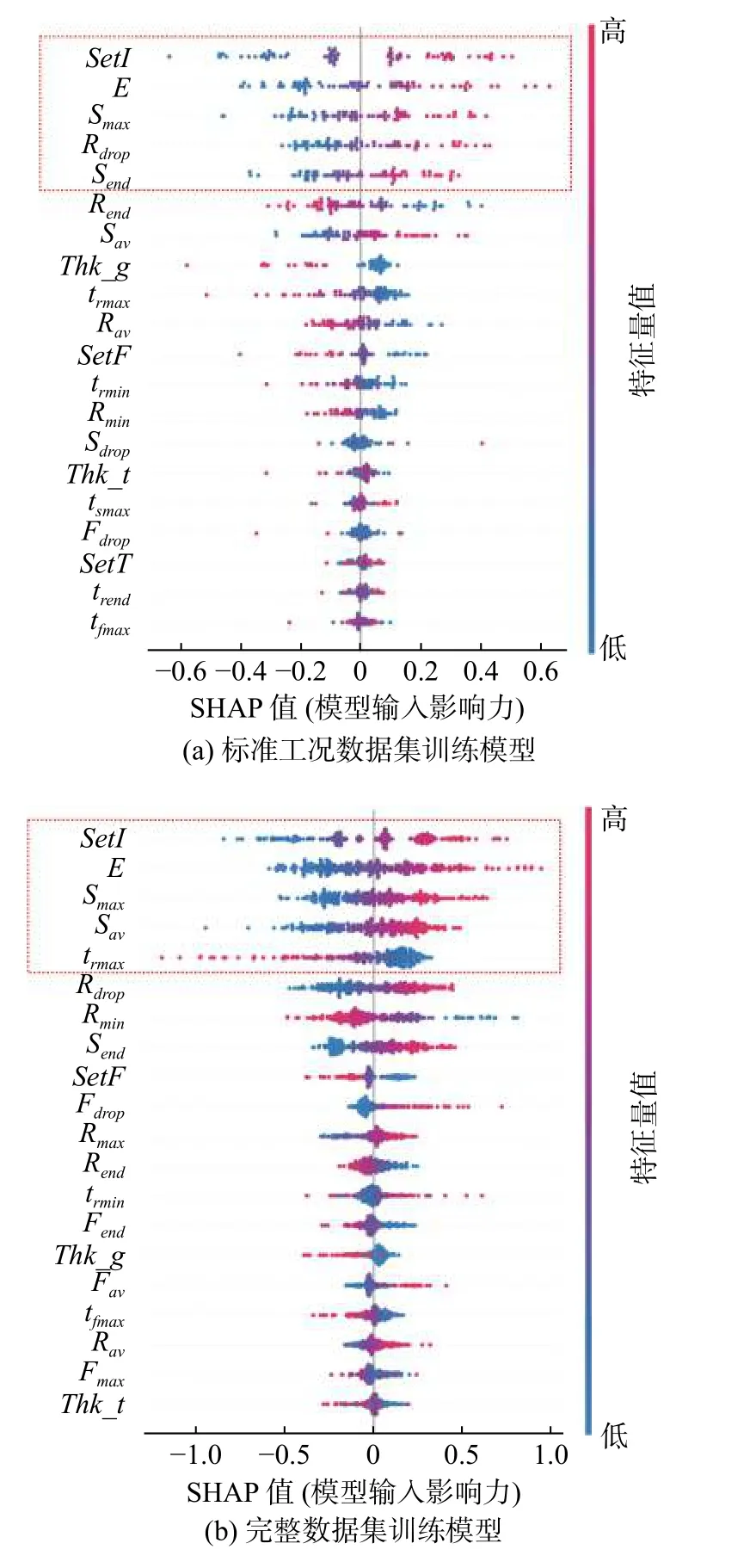
图7 输入特征值对GPR 模型的Shapley 值分布Fig. 7 Shapley value distribution of input features on GPR models. (a) model trained on ST dataset;(b) model trained on ALL dataset

对于标准工况数据集(ST)，最重要的5 个特征量依次为焊接电流SetI、热输入能量E、峰值位移Smax、电阻下降量Rdrop和位移终值Send.这是因为焊接电流增大会增加焊接输入的总能量，进而获得更大的熔核直径，存在明显的正向作用.电极位移主要来自板材受热膨胀，其峰值与最大熔核尺寸正相关[16]，因此Smax对预测值具较大正贡献；位移在峰值后的下降与熔核在焊接后期的收缩相关，因此Send对熔核尺寸预测的贡献为正.电阻在峰值后的下降主要是板材温度升高引起两电极间导电面积增加，而后者往往伴随着熔核直径的增加，所以Rdrop对熔核尺寸预测的贡献为正[17].

对于全部工况数据集(ALL)，模型预测的前三个重要特征量仍为SetI、E和Smax，说明它们在异常工况下仍对熔核直径的预测具有显著贡献.其它两个重要特征量是位移平均值Sav和峰值电阻时刻trmax.在间隙、倾斜等工况下，电极/板材初期接触变化会显著改变焊接生热与散热过程，导致热输入减小[18-19]，熔核尺寸和位移信号均减小；在边距工况下，边缘约束的缺失极易引起焊接飞溅，导致熔核尺寸和位移信号减小[20]，因此，Sav在异常工况下存在更大的预测正向贡献.采用类似分析可知，trmax代表了的焊接前期电阻信号随温度增长的速率，间接表征了焊接加热速率，对熔核尺寸预测的贡献为负.

根据Shapley 值分析结果，SetI、E和Smax对于对工况波动具有较好适应性，而Sav和trmax则对异常工况数据具有一定特异性，这对特征筛选和模型可解释性提升有帮助.此外，标准数据集下贡献最大的前10 个输入特征和完整数据集下贡献最大的前8 个特征均来自工艺参数、电极位移和电阻信号，电极力特征的贡献度普遍偏小.需要研究各传感信号对熔核直径预测模型的重要性.

3.2 输入信号选择对模型精度的影响

前文使用的训练集包括了焊接过程的电阻、电极力和位移信号特征，可能存在冗余.文中分别使用仅焊接工艺参数、来自单一信号的输入特征和来自2 个信号的输入特征训练GPR 模型，对比其应用于ST 数据集和ALL 数据集上的性能，结果见表9.

表9 不同信号特征输入下GPR 模型的预测性能Table 9 Prediction performance of GPR models with different input signals.

仅有焊接工艺参数输入时，模型在2 个数据集上的预测精度均降低，在ST 数据集上A±1mm出现较大性能波动，且在ALL 数据集上显著下降至76.68%，不能满足质量预测需求.当采用单一信号输入特征时，位移信号在ST 数据集获得最佳的模型性能，A±1mm超过94%，其次是电阻信号，电极力信号最差；在完整数据集上，上述排序保持不变，但A±1mm普遍降低5%～ 7%.采用双信号输入特征时，模型在2 个数据集上均能获得较高的预测性能，且两数据集间的性能差异有所减小，这代表多个信号的融合有助于学习异常工况引起的差异与特异性；电阻+电极力信号组合可得到最佳性能，在完整数据集上的A±1mm超过91%，其次是电阻 +位移信号组合.

使用电阻+电极力信号作为输入特征时，在ALL 数据集上获得了比使用全部信号作为输入时更高的A±1mm，意味着去除冗余特征有助于提升模型预测性能.由于现有方案的A±1mm仍不足95%，需在未来对模型结构和输入变量进行更加深入的优化，进一步提高熔核直径的预测精度，从而满足大批量工业生产的需求.

3.3 波动工况对模型泛化性的影响

在输入特征和信号的重要性分析中都发现，波动工况的引入对于模型预测精度具有较为明显的影响.为了明确该影响，文中使用ST 数据集的26个输入特征作为训练集进行GPR 模型训练，使用三种异常工况数据集(即ALL-ST)对模型进行测试，分析模型对异常工况的泛化性能.预测—实测结果对比如图8 所示，预测性能见表10.

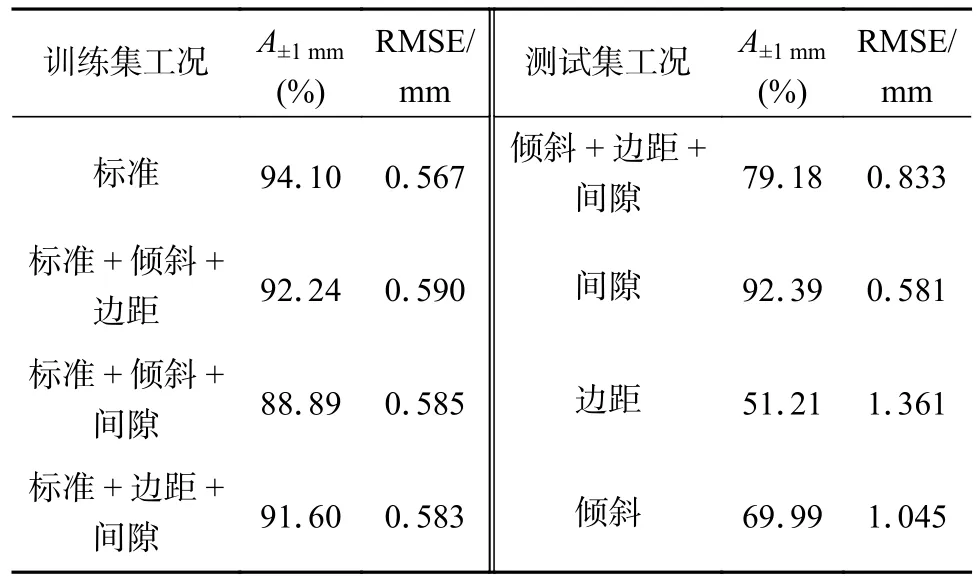
表10 GPR 模型对波动工况的泛化性测试Table 10 Generalization test of GPR model on welding condition fluctuation.

图8 GPR 模型泛化性测试的预测—实测值Fig. 8 Prediction-response results of GPR model generalization test. (a) training result in ST dataset; (b)training result in ALL-ST dataset

可以看出，仅使用标准工况数据训练模型时，模型在异常工况下的精度保持性能较差.训练集上的预测点基本落在误差±1 mm 范围内，但在测试集上的预测点大量位于误差±1 mm 允许界线之外，分布模式存在异常，A±1mm由94.10%降至79.18%.说明仅使用标准工况数据训练的模型的外推性能不足，无法实现异常工况下熔核直径的预测.

为了提升模型对异常工况的适应性，使用标准工况+两种异常工况的组合数据集对模型进行训练，测试其在第三种异常工况数据集上的预测性能，其结果见表10.对比发现，在训练集增加倾斜和边距工况时，模型对间隙工况的泛化性最好，在预测和测试集上的A±1mm均超过92%；而在训练集增加间隙和倾斜或边距工况后，模型在测试集上性能均显著降低，边距工况下的泛化性最差(A±1mm=51.21%)，倾斜工况稍好(A±1mm=69.99%).

上述现象主要源于不同工况下数据特征的分布差异.图9 所示为使用t 分布-随机近邻嵌入模型(t-SNE)对26 个输入特征进行降维和可视化的结果.数据主要分布在两个区域内，区域I 是无飞溅焊接过程，区域II 代表发生了飞溅.可见，间隙和标准工况的输入特征分布较为接近，部分倾斜工况与标准工况差异明显，而边距工况的输入特征分布则与其它三种工况差异较大.引入异常工况对模型泛化性的影响取决于其特征分布与训练数据集的差异.若测试集的特征分布与训练集差异过大，就会导致模型泛化性显著降低.在三种异常工况中，间隙工况对模型性能影响较小，但倾斜和边距工况影响较为显著，若训练集缺少此数据，得到的模型将无法有效预测此工况下的焊点质量.