函数思想在物理强基试题中的应用

王朝祥

(北京市第八十中学)

基础学科招生改革试点也称强基计划,主要是为了选拔培养有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生.从考查内容和能力要求来看,强基试题延续了自主招生试题的特点,并进一步突出对学生数学、物理等基础学科的考查,要求学生能运用数学思想方法分析解决物理问题.

函数描述一个量随其他量的变化关系,变量是函数的基础,对应(映射)是函数的本质.函数思想的应用是指用函数的概念和性质分析问题、转化问题和解决问题.普遍联系和运动变化的观点是函数思想的精髓.高中物理常用的函数有一次函数、二次函数、幂函数、指数函数、对数函数、三角函数,涉及函数的定义域、值域、单调性、奇偶性、周期性、极值等问题.实际应用中,不等式、数列、导数、定积分等问题也属于函数范畴.本文重点讨论函数思想在强基试题中的应用,阐述利用函数思想解决问题的一般思路.

1 利用导数思想,拓展解决问题的思路

函数y＝f(x)在x＝x0处的瞬时变化率,称为函数在该点的导数,记作f′(x0),即

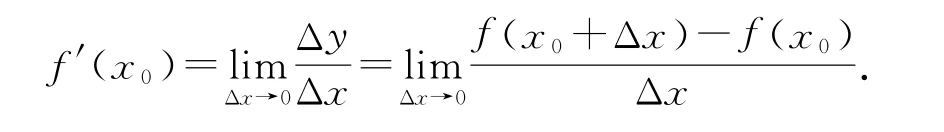
导数f′(x0)反映函数y＝f(x)在x＝x0处的增减趋势和变化快慢.在图像中,导数f′(x0)的几何意义为曲线y＝f(x)在x＝x0处切线的斜率.

高中物理中,很多物理量都是通过变化率定义的,例如,速度是位移对时间的变化率,加速度是速度对时间的变化率,力是动量对时间的变化率,功率是能量对时间的变化率,感应电动势是磁通量对时间的变化率.导数是函数对自变量的瞬时变化率,将导数思想引入物理实际问题,能有效拓宽学生的思路,并能化解仅用初等数学知识难以解决的问题,提升学生运用数学工具处理物理问题的能力.现结合一些常见问题举例说明.

例1 (2011年华约自招)如图1所示,纸面内两根足够长的细杆ab、cd都穿过小环M,杆ab两端固定,杆cd可以在纸面内绕过d点并与纸面垂直的定轴转动.若细杆cd从图示位置开始,按照图中箭头所示方向,以匀角速度转动,则小环M的加速度( ).

图1

A.逐渐增加

B.逐渐减小

C.先增加后减小

D.先减小后增加

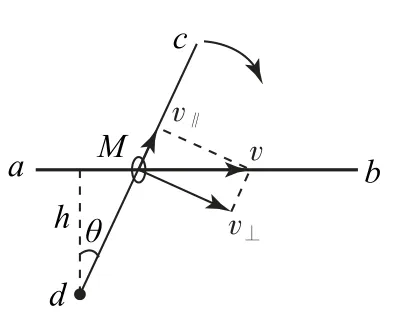
图2

例2 (2015年清华领军计划)在距离水面高度为h的岸上,有人用绳子经定滑轮拉着小船靠岸,人收绳子的速率恒为v0,当小船与岸边的水平距离为s时,其速度、加速度分别多大?

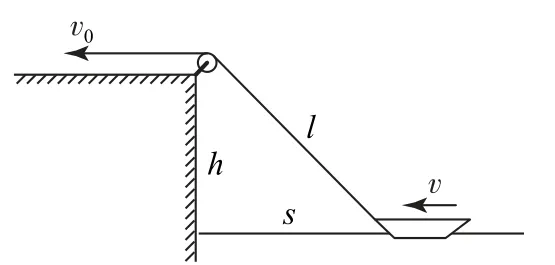
图3

2 利用定积分化解连续函数求和问题

定积分的本质是连续函数的求和,其在高中物理中的应用涉及速度或位移的计算、液体压力的计算、变力做功问题、物理量的平均值问题、转动惯量问题、连续带电体电势的计算、交流电有效值的计算等.在物理教学中适当渗透定积分“分割—建立微元—求和”的思想方法,有助于学生对物理概念的准确理解和辨析,进而提升学生运用数学知识处理物理问题的能力,拓展思维空间.

例3 (2017年北大综合营)一盛水的容器绕竖直中心轴匀速转动,求容器内水面形状.

如图4所示,取旋转液面表面任意位置(x,y)处的小水珠,质量记为m,该处液面切线与水平方向夹角记为θ.在旋转的非惯性系中分析水珠受力,考虑惯性力,三力平衡,且有

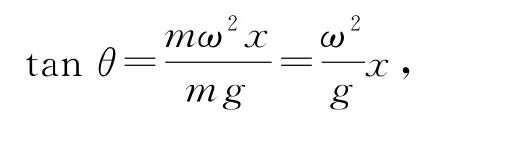
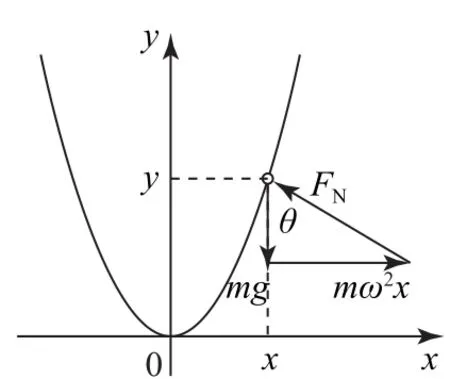
图4

3 函数思想在极值问题中的应用

分析物理中的极值问题常涉及代数、几何、向量、微积分等多个数学分支,对学生的分析综合能力和应用数学知识解决物理问题的能力要求较高.解决极值问题的一般思路是认真分析物理情境,根据物理中的定理或定律建立因变量与自变量之间的函数关系,再利用数学方法求极值.在上述过程中,函数构建是解决问题的关键.

例6 一均匀细杆置于粗糙地面上,人对其一端施力,力与杆始终垂直,要将杆无滑动地慢慢抬到竖直位置,则杆与地面之间的静摩擦因数至少应该多大?

如图5所示,对杆受力分析,列共点力平衡方程有Fcosα＋FN＝mg,Fsinα＝Ff,以A点为轴,由转动平衡有

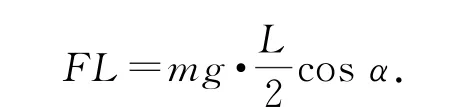
图5

若n个数x1、x2、x3、…、xn的和为定值,当这n个数都相等时,它们的积有最大值;若n个数x1、x2、x3、…、xn的积为定值,当这n个数都相等时,它们的和有最小值.

例7 (2013年华约自招)明理同学平时注意锻炼身体,力量很大,最多能提起m＝50kg的物体.一重物放置在倾角θ＝15°的粗糙斜面上,重物与斜面间

如图6 所示,设该同学拉动重物的力F的方向与斜面成角度α,根据力的平衡,若重物刚好能被拉动(a＝0),在垂直于斜面方向有

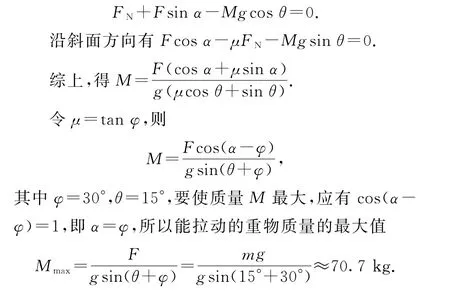
图6

本题考查共点力的平衡,要求学生能熟练列出力的平衡方程,并能运用三角函数知识求极值,对数学运算能力要求较高.

若引入摩擦角和全反力的概念,本题可以采用矢量图解法分析,解题思路大为简化.

如图7所示,斜面对重物的支持力FN与最大静摩擦力Ffm的合力称为全反力R,全反力与支持力的夹角φ称为摩擦角,tanφ＝μ,用R等效代替FN与Ffm,本题转化为三力平衡问题.

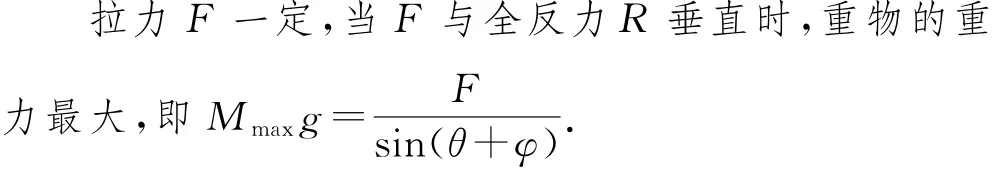
图7

综上所述,函数思想在强基试题中有广泛的应用.利用函数思想解决物理实际问题的一般思路如下:1)根据物理情境梳理相关物理量之间的函数关系,从而把物理模型转化为数学模型;2)经过数学演算、推理得出结果;3)再结合物理情境讨论数学结果的物理意义,得出符合实际的结论.在上述环节中,函数构建是解决问题的关键.