傍河取水对河水和地下水的影响分析
2023-01-07姚旭初张琦伟杨良权
汪 琪,姚旭初,张琦伟,魏 红,杨良权
(北京市水利规划设计研究院,北京 100048)
在河道治理工程中,岸滤系统[1-2]是河道修复和治理水污染的一种新型的理念,傍河取水使这一系统作用发挥得到强化,诸多学者对岸滤系统中的水化学和水生物的变化进行了研究,本文重点研究傍河取水对河水和地下水的影响,为界定岸滤系统范围[3]提供技术参考。研究这个问题,关键因素就是河流情况和水文地质情况,河岸取水根据河流形态可分不同情况,为了方便分析问题水文地质专家将河流刻画成井的形式,把深大切割含水层的河流划分为完整河流,其余就是非完整河流。完整河流在岩溶地区多发育,但非完整河流的分布在我国更为普遍,国内学者对非完整河流有较多研究,主要集中在认识水文地质条件、求取相关参数以及地表水和地下水的联系等方面。本文为研究傍河取水的影响,针对以粉细砂为主的非完整河流在傍河取水时对激发河水入渗能力和对地下水的影响进行研究。希望对傍河取水的影响研究和界定岸滤系统范围提供一些有益的参考。
1 研究现状分析
河流完整性与否由河流与含水层的切割关系确定,切穿含水层的为完整性河流,否则为非完整性河流,用非完整度刻画[4-5]。傍河取水主要研究水文地质参数、地下水和河水的水力联系、水资源评价等,近年来着眼于岸滤系统生态分析。 我国北方多非完整河流,所以对非完整河流的傍河取水研究意义较大。目前研究傍河取水主要的方法有解析法、数值模型法、和试验方法。
完整河流已经有长足发展的解析模型,通常认为解析法只适用于研究理想状态或者结构简单的含水层[6]。一是通过镜像法可以求解完整河流附近的含水层的渗透系数[7],二是通过裘布衣的稳定流公式可以计算傍河取水潜水含水层的渗透系数。解析法适用于处理完整河流水文地质条件简单的含水层。
借助数值模型分析地下水和河水的水力联系是最常用的方法。河流处理上,完整河流通常可以概化为定水头边界[8],而非完整河,在河床底部设置弱透水的缓冲区模拟效果较好[9],或者非完整河可通过简易河流-含水层水力耦合模型进行模拟[8]。研究模拟非完整河和地下水的相互转换关系,最好是在已经准确求得含水层渗透系数的前提条件下进行。当考虑河流的规模尺度时,模拟小型河渠,有研究认为小型河渠不能概化为定水头边界[10],因为小型河渠基本都是非完整河流,河流两侧的地下水是相互联系的整体,取水过程中会相互影响。对于河床宽阔的大型河渠,傍河取水有所不同。
试验法有野外试验和室内试验。野外试验是现场傍河取水,有学者利用野外试验研究地下水[11]和河水的水力联系时,发现忽略了河流的非完整性,在河水和地下水水力联系弱的情况下,计算的河水渗漏量偏大[12]。室内模拟试验通常是连续介质电模拟试验[13],但是室内试验未涉及河流的宽度、河流非完整性、和河底渗透性特征,并且岩土样易受扰动,与实际情况差别较大。
本文利用现场傍河取水试验资料通过解析法求取研究区水文地质参数,在获得含水层渗透系数的前提下建立剖面数值模型,分析不同傍河距离下傍河取水对河水和地下水的影响。
2 研究区概况
本文选取北京温榆河流域北运河下游河段杨洼闸桥附近抽水试验进行研究分析。研究区位置见图1。
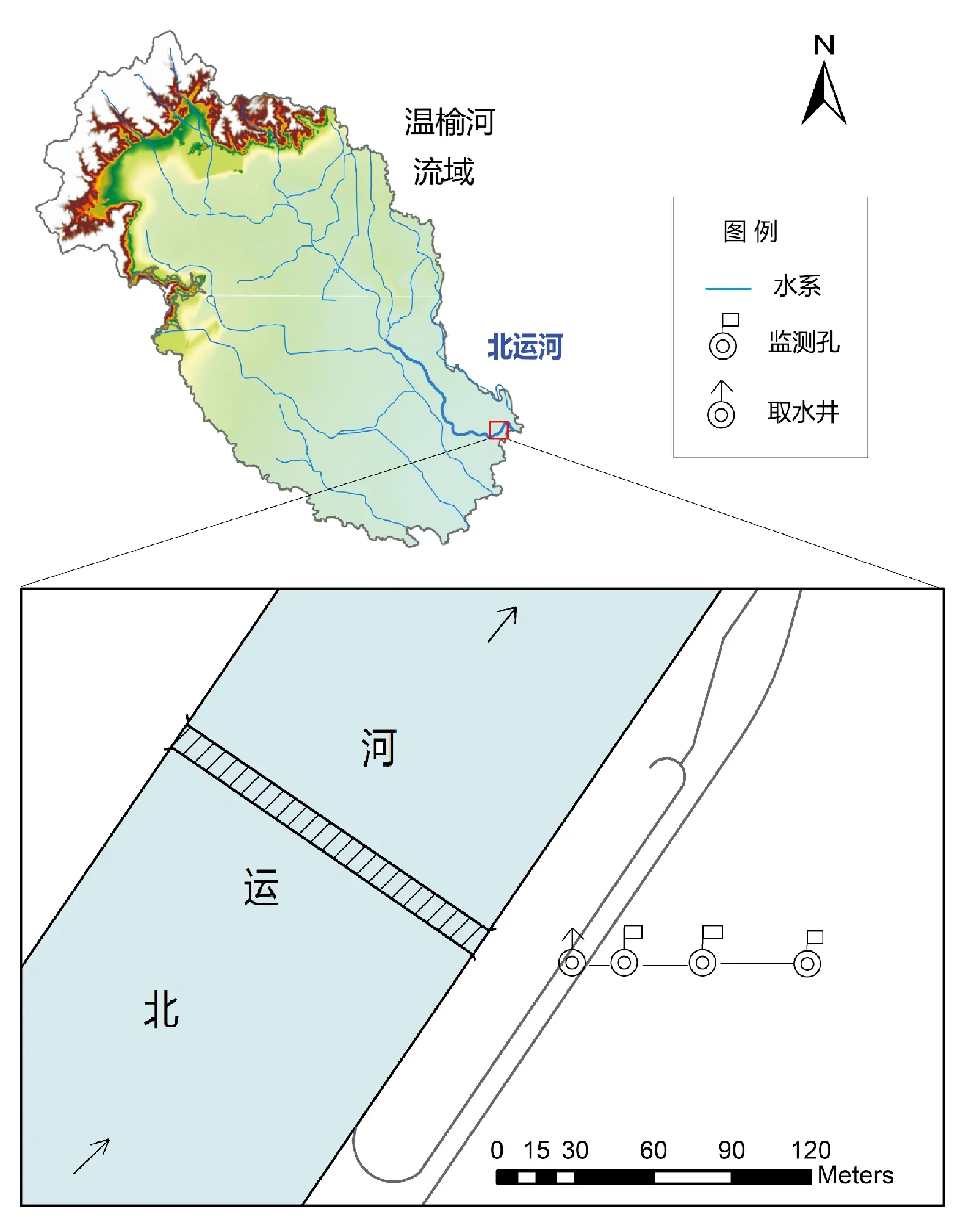
图1 研究区位置和傍河取水平面布置
场区位于北运河冲洪积下游平原,潜水含水层底板埋深约30 m,岩性以粉细砂和细中砂为主,底部可见中粗砂夹圆砾;临河取水布置为取水井和监测井。取水井靠近河流,监测井垂直于河流布置。非完整河宽约130 m,监测井傍河距离约25 m,河床宽度远大于取水井到河边的距离。临河取水前,恰逢河道清淤,增强了河水和地下水之间的水力联系。初始潜水水位高程平均约为10.5 m,河水水位约10.9 m,河水略微补给地下水。概化后的场区水文地质剖面见图2。

图2 研究区水文地质条件概化图
3 研究区水文地质参数
对于傍河取水,地下水动力学[7]给出了镜像法计算含水层的渗透系数的方法,对于镜像法而言,应用于完整河流或是河床宽阔的非完整河流,有三个必要条件:一是要求河水和地下水水力联系密切,这样在傍河取水过程中,会有充足的河水转换为地下水补给井取水量,使得近河侧取水量在后期主要来源于受河水补给的地下水,充足的侧向渗流就仿佛一口注水井,相反,河底如有很厚的淤积层,阻隔河水和地下水水力联系,则不适用于镜像法(见图3(a))。二是影响半径宜大于取水井到河边距离。比如取水量较小,影响半径小于取水井到河边距离,这样即使是临河取水,实质上河流渗漏对取水井本身影响很小。三是因傍河取水激发的河流渗漏量占到取水量的一半以上。这里注意取水量的一半是指激发的河水渗漏量,而非取水水源中的一半源自渗漏的河水。如小河或小沟渠,河水流量小,侧向渗流量占比很小则不适用(见图3(b))。

图3 不适用镜像法的傍河取水情形
利用镜像法求解含水层渗透系数公式如下:
(1)
式中:r1为计算点距取水井的距离,取水井时r1=2a,a为水井到河边的距离;r2为计算点距镜像虚井的距离,取水井时r2=rw,rw为水井半径;Δh2为计算点处Δh2-lgt关系曲线上的纵坐标值;Q为取水流量。
本研究区利用镜像法计算含水层渗透系数,选取监测井1(兼取水井)、监测井2和监测井3的试验数据参与计算,排除监测组孔,因其分段监测数据不能完整代表整个潜水水位动态特征。镜像法计算得出场区潜水含水层渗透系数13 m/d~14 m/d,见表1。该渗透系数为取水点至监测点方向上整个含水层深度上的综合性参数。

表1 利用后期数据计算渗透系数
显然,从镜像法的适用条件可以看出,凡适用镜像法求解含水层渗透系数的情况均大量激发地表水入渗,即河岸渗透强烈发生,水循环快,渗滤作用强。
下面借助数值模型来模拟傍河取水-恢复过程,一方面验证适用镜像法的傍河取水激发的河水入渗量占取水量的一半以上这一条件,另一方面预测不同傍河距离下傍河取水对激发河水入渗能力以及对地下水的影响。
4 数值模型分析
4.1 数学模型建立
根据场区水文地质条件和傍河取水布置,利用GMS软件中的modflow模块开展非稳定流剖面数值模拟,数学模型如下:
式中:K为潜水含水层渗透系数,m/d;μ为潜水含水层给水度;H为地下水位高程,m;B为含水层底板标高,m;ε为源汇项,m/d;H0为初始地下水位,m;q为边界上单位宽度的地下水补给( 或排泄) 量,m/d;Kr为河床弱透水层渗透系数,m/d;M为河床弱透水层厚度,m;Hr为河水位,m;W为河流宽度,m;x,z为剖面坐标,m;D为研究剖面范围;t为时间;n为法线方向;Γ2、Γ3为二类及三类边界。
4.2 应力期划分
为了清晰的展示取水初期和恢复初期的对地下水的影响及模拟恢复的确切时长,根据地下水监测划分应力期,共188个应力期,模拟总时长244 h,共计模拟2 313个时间步长。模型中时间单位为h。由于监测数据最小单位为准,所以时间精确到min。包括初始潜水位核准期分2个应力期,均为24 h,时间步长为1。取水过程分88个应力期,共70 h,分别为4个1 min、3个2 min、4个5 min、3个10 min、3个20 min、6个30 min,65个1 h,每个应力期均细分为10的时间步长数。恢复过程分98个应力期,共126 h,分别为4个1 min、3个2 min、4个5 min、3个10 min、3个20 min、6个30 min,73个1 h、2个24 h。除最后的2个应力期,每个应力期细分为240个时间步长数外,其余每个应力期均细分为10的时间步长数。
4.3 模型网格剖分
模型网格剖分为水平5 m×垂向2 m,厚度为20 m。剖面模拟水平宽度660 m,垂向深度30 m。由于取水井降深较大,将剖面模型前8层合并为一大层进行模拟,避免网格的疏干,见图4。

图4 剖面数值模拟边界条件及网格剖分(垂向扩大4倍显示)
4.4 水文地质概念模型
4.4.1 含水层及参数概化
该河道场区垂向上依次呈粉细砂、细中砂、砂夹圆砾的沉积层理结构[14],反应出河流在历史上由急到缓的变化,各地层概化为均质各项同性,各层渗透系数和给水度见图5,综合渗透系数为14 m/d,与镜像法计算的渗透系数保持一致。

图5 模型中地层及渗透系数分布(综合渗透系数约14 m/d)
4.4.2 边界条件概化
模型上边界为潜水位,下边界粉质黏土层为隔水边界,但监测井2底部处存在“天窗”[14],处理为通用水头边界。场地两侧较远处地下水水位较稳定,处理为通用水头边界,见图4。
(1) 初始流场。地下水以水平流为主,初始水位为根据取水前两天观测到的实际地下水水位进行稳定流模拟得到的水位,见图6。

图6 模型中初始流场图(稳定流模拟的结果)
(2) 通用水头边界。通用水头边界中的传导系数,它假设外部足够远处有一个很稳定的补给水头hb,根据模型边界处水位的变化不断的给予补给或接受排泄,将达西定律表达的补给水量转换为模型表达时,用水头差Δh和传导系数Cb表示。水头差为模型边界计算潜水位和外部水头hb之间的差值,是一个动态值,由模型自动计算。
(3)
式中:A为模型中外部水流入或内部水流出断面的面积,Cb为边界处传导系数。
模型两侧通用水头边界的一个单元网格A=2×20=40 m2,路径长度L=5 m,综合渗透系数K=14 m/d;天窗处网格的A=20×5 m2,路径长度L=2 m,“天窗”下方承压含水层渗透系数取0.40 m/h。通用水头边界处每个网格参数见表2。

表2 模型中通用水头边界
(3) 河流处理。场区河流宽W=130 m,用river程序包处理,模型中河流概化见图7,由于本场区取水前清淤,河底淤泥层被清除或者局部很薄,模型中河流底淤积层岩性为粉砂或砂质粉土,估计厚度M=1 m,淤泥层渗透系数Kr=0.65 m/d,模型中河流长度为L=20 m。
河流程序包[15]中用淤泥层传导系数CRIV、河水位HRIV、淤积层底高程RBOT三个参数表示。
(4)
模型中河水和地下水的交换量QRIV:
(5)
当潜水位h高于淤积层底,用河水位减去潜水位的水头差计算河水和地下水的交换量;当潜水位低于淤泥层底,用河水位和淤泥底高程差参与计算河水与地下水的交换量。本模型中的河流程序包参数如下表3。

表3 模型中河流边界

图7 模型中河流概念图
(4) 取水井处理。定流量傍河取水,取水量为132 m3/h。取水井出水量按泵吸力在垂向上进行人为分配,其中在泵吸水段处含水层出水量最大(见图8),由于试验时间很短,忽略降水和蒸发。

图8 井出水量分配
4.5 模型校核
潜水监测井位置设置在滤水管的上端。校核期为整个抽水-恢复监测过程,抽水期有89个监测数据(监测频次为1 min、2 min、5 min、10 min、30 min、60 min),恢复期有96个监测数据(监测频次为1 min、2 min、5 min、10 min、30 min、60 min),模型水位校核目标置信区间[-1,1],取水井和监测井抽水-恢复过程拟合曲线见图9—图11,拟合效果较好。
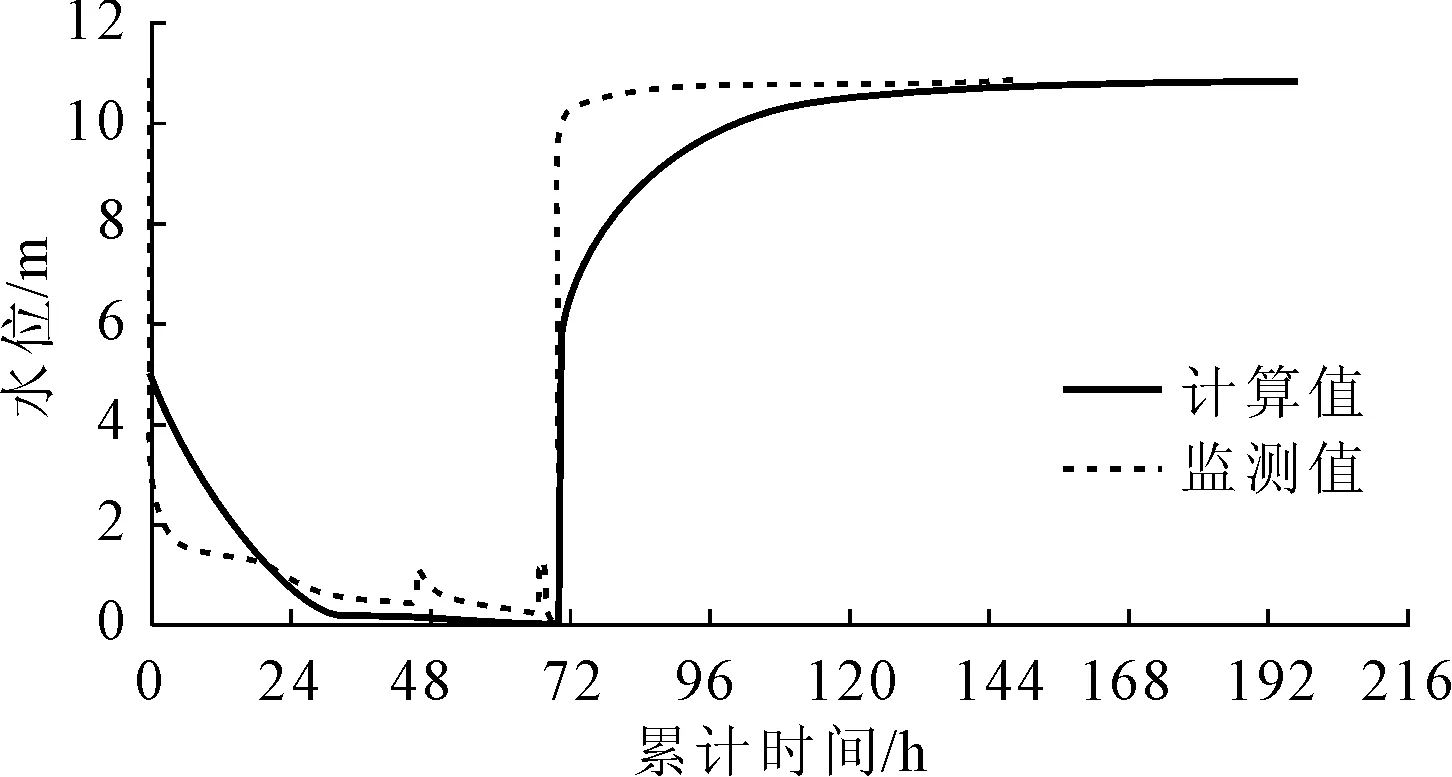
图9 监测井1水位拟合曲线
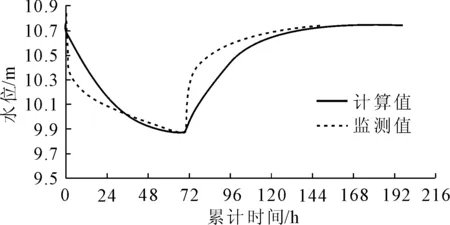
图10 监测井2水位拟合曲线
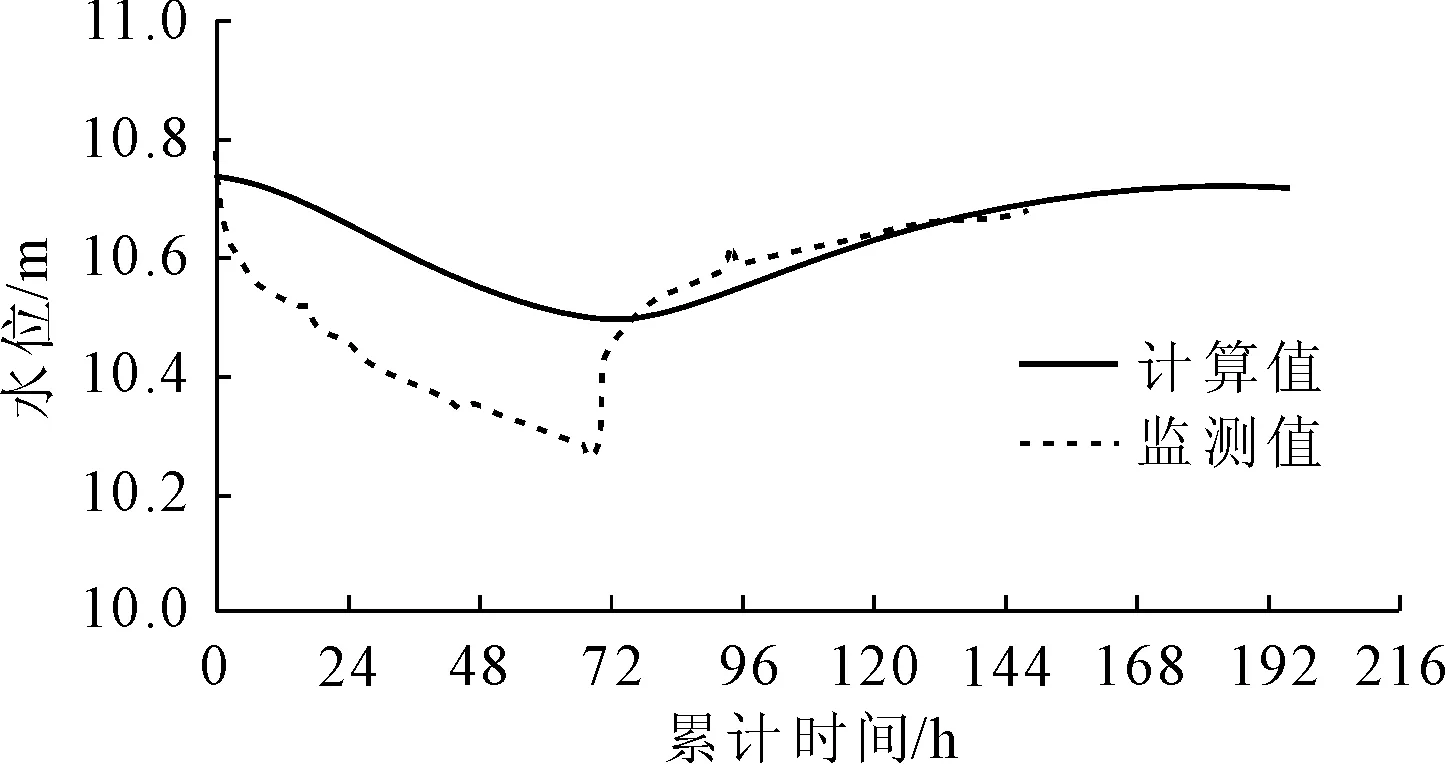
图11 监测井3水位拟合曲线
根据Nash效率系数:
(6)
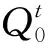

表4 Nash效率系数
Nash效率系数在区间(0.862~0.030),表示取水井附近区域模型质量好,模型可信度高;远离取水区域,模拟结果接近观测值的平均值水平,总体结果可信。
4.6 取水-恢复过程模拟
傍河25 m取水-恢复过程模拟,从水均衡看,此次河岸取水初期弹性释水,水主要来自含水层储存量,开采激发了河流渗漏补给,随着水位持续降低,河水渗漏量增加,来自储存量的水减少。取水初期,地下水水头降低,激发河水渗漏,取水24 h后河水渗漏补给量约占取水量的50%以上,水均衡见表5。

表5 模型中的水均衡
根据地下水流场速度矢(见图12和图13),从速度矢看,近河侧,取水井接受河水补给,傍河越近,河水补给速度越快,傍河越远,河水补给越慢,见图12。其次,本取水-恢复模型显示,临河侧取水影响范围约75 m,而远河侧取水影响范围约80 m,临河取水在临河侧的影响范围和远河测大体一致,影响最远的深度位置大致在泵吸水段,离泵越远,影响相
对减弱。再次,临河侧,抽水72 h时河水对地下水的补给范围约40 m,为本河流河宽的0.31倍。
取水3 d后水位下降趋势变缓,具有稳定流的特征。数值模拟的含水层综合渗透系数约14 m/d,与解析法结果较一致。取水影响范围大于取水井至河边的距离,河水在取水量中的比重超过一半。河水和地下水水力联系密切。这些也验证了本取水试验适合镜像法的计算。
此外,从图12和图13也可以看出,“天窗”补给在取水和恢复过程的作用,取水井周围地下水位快速降低,加大水头差会激发“天窗”补给,随着水头差的持续增大,这种补给量也增大,在取水过程中“天窗”补给经历小平稳补给-扩大补给-大平稳补给三个状态;恢复时,伴随着失稳又经历快速补给-缓慢补给-稳定下来三个状态,直到整个地下水基本恢复初态,“天窗”补给才相对平稳下来。

图12 取水过程中速度矢变化

图13 恢复过程中速度矢变化
4.7 激发入渗模型预测
为了模拟取水井傍河距离对河流入渗范围的影响,在取水井取水量相同的条件下,改变取水井傍河距离,设置三种傍河距离情景50 m、100 m、150 m,分别进行预测模拟。
(1) 取水傍河距离50 m。河岸取水初期弹性释水,水主要来自含水层储存量,开采激发了河流渗漏补给,加大了天窗越流补给,取水24 h后河水渗漏补给量约占取水量的28%,取水48 h后河水渗漏补给量约占取水量的38.8%。
根据地下水流场速度矢(见图14),临河侧取水对地下水影响范围约95 m,而远河侧取水对地下水影响范围约105 m,取水两侧对地下水的影响范围较一致。取水72 h时河水对地下水的补给范围约25 m,为本河流河宽的0.19倍。

图14 情景一取水72 h地下水速度矢
(2) 取水傍河距离100 m。河岸取水初期弹性释水,水主要来自含水层储存量,开采激发了河流渗漏补给,加大了天窗越流补给,取水24 h河水渗漏补给量约占取水量的4.1%,取水48 h后河水渗漏补给量约占取水量的6.4%。
根据地下水流场速度矢(见图15),临河侧取水对地下水影响范围约125 m,而远河侧取水对地下水影响范围约145 m,取水两侧对地下水的影响范围相差不大。取水72 h时河水对地下水的补给范围约10 m,为本河流河宽的0.07倍。
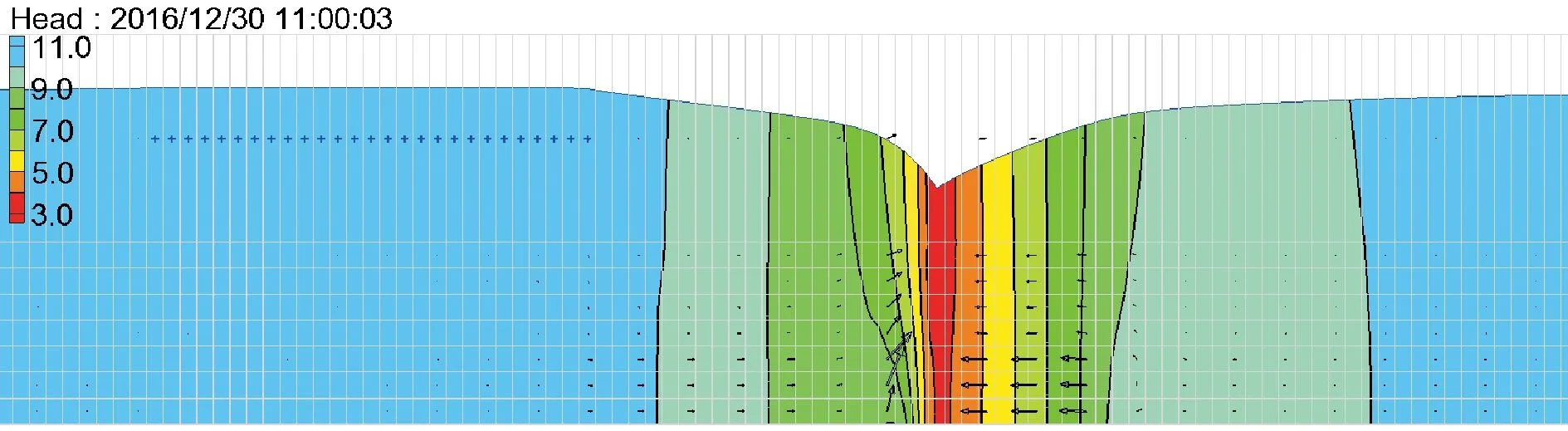
图15 情景二取水72 h地下水速度矢
(3) 取水傍河距离150 m。河岸取水初期弹性释水,水主要来自含水层储存量,开采激发了河流渗漏补给,加大了天窗越流补给,取水24 h河水渗漏补给量约占取水量的1.5%,取水48 h后河水渗漏补给量约占取水量的2.2%。
根据地下水流场速度矢(见图16),临河侧取水对地下水影响范围约145 m,而远河侧取水对地下水影响范围约170 m,取水两侧对地下水的影响范围相差不大。取水过程河水对地下水的影响极小。
综上, 综合取水条件下三种情况的模拟结果见表6,模型激发河水渗漏,粉细砂为主的河床,临河取水激发河流入渗,取水井傍河越远,激发河水入渗的能力就越弱。当取水井傍河距离超过含水层厚度时,取水稳定时的河水入渗量占取水量的比重不足一半。同时,还可以看出,在模拟的傍河距离范围内,随着取水井傍河距离逐渐增大,产生的对地下水的影响范围也逐渐增大。粉细砂地区傍河距离150 m时傍河取水对河水的影响微乎其微,取水量主要来源于地下水。

图16 情景三取水72 h地下水速度矢

表6 取水条件下几种情况的模拟结果
5 结 论
(1) 傍河取水镜像法的应用要满足三个条件:一是河水和地下水水力联系密切;二是取水影响半径宜大于取水井到河边距离;三是因傍河取水激发的河流渗漏量占到取水量的一半以上。对于河底有深厚淤积层和小沟渠型的非完整河流不适用镜像法求参。
(2) 利用镜像法计算了研究区含水层渗透系数,应用效果较好。同时建立了剖面数值模型,模拟了傍河取水-恢复过程,模型显示傍河取水的河水入渗量占取水量的比重50%以上,进一步验证了镜像法的适用性。
(3) 研究区为河水和地下水水位接近的粉细砂场区,借助剖面数值模型分析了傍河取水激发河水入渗,在取水情况不变的前提下,预测不同傍河距离50 m、100 m、150 m时傍河取水对激发河水入渗能力的影响和对地下水的影响,发现随着傍河距离的加大,激发河水入渗的能力逐渐降低,对地下水的影响范围逐渐增大。粉细砂地区傍河距离150 m时傍河取水对河水的影响微乎其微,取水量主要来源于地下水。
以上研究对以粉细砂为主、河床宽阔的非完整河流地区进行河道治理工程、生态修复工程等水生态工作具有一定参考价值。
