水工高性能钢筋混凝土面板靶向激励响应分析

喻 江，徐海峰，张卫云

(1.南京水利科学研究院， 江苏 南京 210024；2.南京市水利规划设计院股份有限公司，江苏 南京 210022)

为满足新时代面板结构向大跨度、大宽度、大荷载、高要求、高标准的发展需要，高性能面板结构以其优良的力学性能在工程中被广泛使用，体现出显著的经济效益和环保效应[1-3]。

靶向动力作用是一种延伸到高频阶段频率的高强度、持续时间短的应力波脉冲传播，在极短间隔时间内靶向作用接触点发生高于静态量级的应变速率变化，表现出与静态过程明显不同的力学行为特征。由于靶向作用具有瞬时性、冲击性、集中性与针对性，对工程结构带来诸多不利，国内外专家与学者在大量试验研究的基础上，对钢筋混凝土面板结构的靶向性能进行了相关的研究。

Gopinath等[4]对纤维钢筋混凝土面板进行了低速、高速靶向作用下结构从受到损伤到失效再到破坏三个方面的动力特性研究。Anil等[5]和Husem等[6]通过设计不同尺寸试件与不同边界约束条件，详细探讨了钢筋混凝土面板在靶向荷载下的动力行为，得到了靶向荷载、位移响应、靶向能量与破坏模式的研究结论。Subashini等[7]将平滑粒子流体动力学(SPH)与有限元法进行结合来模拟混凝土损伤及破坏模式，并通过可靠性函数来评估动力行为。Verma等[8]和Othman等[9]通过提出混凝土的损伤塑性本构模型(CDP)，对超高性能纤维钢筋混凝土梁(UHP-FRC)进行了不同靶向荷载率下的破坏分析。Elavarasi等[10]通过落锤试验对砂浆填充纤维混凝土板(SIFCON)进行了低速靶向下的破坏性研究。顾培英等[11]采用逐级递增循环靶向加载方式研究了靶向荷载下砂浆板的破坏特征及靶向力、靶向能与最大加速度响应间关系。

国内外学者对靶向作用下的钢筋混凝土结构的动力特征研究主要从理论分析、试验研究和数值模拟3个方面进行[12-16]。理论分析方面：通过拟静力法得到了靶向提高系数，并借助试验测试从而获得经验公式，该种方法没有考虑阻尼等影响因素；通过动力分析法建立质体运动方程，获得了其靶向力、相对位移等动力学参数。试验研究方面：通过自由落锤试验，获得了靶向力时程、加速度时程、位移时程、应变时程等动力参数；同时进行了单次靶向与累积靶向下的破坏试验；通过试验进一步进行了钢筋配筋率、混凝土强度等敏感参数分析。数值模拟方面：进行了动态非线性有限元分析，通过网格划分、本构模型的选择、动力参数的给定几个方面进一步完成了扩展有限元参数评估分析。

基于靶向激励因素和高性能面板结构靶向激励响应下的计算方法研究，提出水工高性能钢筋混凝土面板模型，以此开展靶向激励响应作用下的特性试验与空间分布特征研究。

1 靶向激励机理

1.1 模型及基本参数

靶向激励是基于能量守恒定律对研究对象进行定向靶向，其作用过程是通过借助摆锤的势能转换形成的靶向功施加靶向激励，摆锤靶向激励原理如图1所示。激励系统由具有特定质量的锤头(mp)，便于形成有效锤矩的特定长度(Lp)，以及摆锤预扬角(θp)几部分组成。

图1 摆锤靶向激励模型

可得摆锤在对测试物进行靶向激励作用过程中的能量守恒等式如下：

(1)

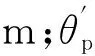
根据摆锤靶向激励过程中的动量定理，可得摆锤对测试物靶向激励作用表达式如下：

(2)

式中：tp为摆锤激励作用时长,s；Fp为靶向激励荷载,kN。

由式(2)可得摆锤的靶向激励冲量Ip(N·s)。

通过引入Dirac Delta函数来表征摆锤进行靶向激励时的作用位置，建立摆锤靶向激励荷载位置函数(见图2)，表达式见式(3)：

(3)

(4)

(5)

1.2 靶向激励接触系数

如图3所示，进一步构建摆锤靶向激励接触系数(ICC)来表征摆锤与被测物体的激励关系。靶向激励接触系数由摆锤锤头材质、摆锤锤头形状、摆锤锤头质量、靶向激励速度、被测物体材质几种因素构成，其表达式可表达为：

(6)

式中：Sp为靶向激励接触面积,m2；Ep为摆锤锤头的弹性模量,Pa；Ec为被测物的弹性模量,Pa。

其中靶向激励接触面积函数表达式为：

(7)

图2 靶向激励位置函数图

图3 靶向激励原理图

1.3 靶向激励响应解析解

进行水工高性能钢筋混凝土面板靶向激励机理分析时，满足如下基本假定：(1)面板材料各向同性；(2)面板各处均匀厚度；(3)边界条件满足固定端对称约束；(4)靶向激励产生的竖向挠度远小于面板厚度；(5)忽略构造筋的影响。

可得水工高性能钢筋混凝土面板的剪力、弯矩表达式分别为：

(8)

(9)

(10)

(11)

(12)

(13)

式中：I为面板的抗弯刚度；μ为面板的泊松比。

通过式(8)—式(13)建立内力平衡等式有：

(14)

(15)

(16)

由式(3)、式(14)—式(16)确定水工高性能面板摆锤靶向激励机理方程为：

(17)

令函数φmn(x,y)作为建立模型的靶向激励边界函数条件，n代表阶数，m代表与n阶对应的取值编号，其表达式为：

φmn(x,y)=[amsin(ρ1mnx)+bmcos(ρ1mnx)+

cmsh(ρ2mnx)+dmch(ρ2mnx)]sin(fny)

(18)

该模型对应的边界条件为：

(19)

(20)

(21)

(22)

将式(18)代入式(19)—式(22)，求得靶向激励边界函数φmn(x,y)：

φmn(x,y)=

(23)

引入式(3)的靶向激励条件，进一步可得水工高性能面板在摆锤靶向激励作用下的加速度响应函数表达式：

(24)

2 靶向激励动力特性试验

2.1 试验概况

经过推导验证分析，当采用相同材料时，本模型还需满足以下相似条件：

SL=SB=SH

(25)

Sδ=St=Sε=Sv=SF=1

(26)

式中：L、B、H分别为模型的长度、宽度和厚度；δ、t、ε、v、F分别为靶向激励位移、靶向激励时间、靶向激励应变、靶向激励速度、靶向激励荷载。

本次研究设计和制作了2块水工高性能面板模型，模型尺寸均为：长1.35 m，宽1.00 m，厚0.08 m。钢框架基础包括H型钢梁和矩形钢-混凝土组合柱(含钢率为0.0882)，其中，H型钢梁长1.0 m，高100 mm，翼缘宽100 mm，厚10 mm，腹板宽10 mm，高80 mm。高性能混凝土配合比为：水泥∶砂∶石∶水=1.00∶1.20∶1.92∶0.29，JM-8掺量1.8%，矿物掺合料掺量30.0%，钢纤维体积掺量1.0%。水工高性能面板通过高强螺杆与钢框架基础连接成为剪力连接程度为1.0的水工高性能面板模型，构造参数见表1。采用摆锤获得靶向激励能量，从而对水工高性能面板模型施加靶向激励作用，2种模式下的靶向激励参数见表2。模型试验如图4所示。

表1 水工高性能面板模型构造参数表

表2 摆锤靶向激励试验参数表

图4 水工高性能面板靶向激励模型试验

2.2 靶向激励响应试验分析

模型PHPCCP1与PHPCRCP1在摆锤靶向激励作用下靶向荷载历时特性如图5与图6所示，其中，IF表示靶向激励荷载,kN;IT表示靶向激励历时,ms。

图5 PHPCCP1模型摆锤靶向激励荷载历时特性

由图5模型PHPCCP1试验测试结果可得：在靶向激励工况M1下，靶向激励历时0.62 ms，靶向激励峰值荷载达13.341 kN，峰值荷载时刻为12.15 ms；在靶向激励工况M2下，靶向激励历时0.57 ms，靶向激励峰值荷载达19.546 kN，峰值荷载时刻为10.93 ms。由图6模型PHPCRCP1试验测试结果可得：在靶向激励工况M1下，靶向激励历时0.59 ms，靶向激励峰值荷载达14.606 kN，峰值荷载时刻为2.28 ms；在靶向激励工况M2下，靶向激励历时0.61 ms，靶向激励峰值荷载达20.253 kN，峰值荷载时刻为5.87 ms。

图6 PHPCRCP1模型摆锤靶向激励荷载历时特性

根据图5、图6可得模型PHPCCP1与PHPCRCP1在不同激励工况下的靶向激励特征参数见表3。

表3 摆锤靶向激励特征参数表

由表3分析可知：模型PHPCCP1在激励工况M1作用下，靶向激励能量实测值与理论计算值分别为4.024 J和4.170 J，实测值是理论计算值的0.97倍，在M2作用下，靶向激励能量实测值与理论计算值分别为7.302J和8.338J，实测值是理论计算值的0.88倍，误差在3%～12%，吻合度高；模型PHPCRCP1在激励工况M1作用下，靶向激励能量实测值与理论计算值分别为4.368J和4.170J，实测值是理论计算值的1.05倍，在M2作用下，靶向激励能量实测值与理论计算值分别为8.978J和8.338J，实测值是理论计算值的1.08倍，误差在5%～8%，吻合度高。

进一步对模型PHPCCP1与PHPCRCP1在摆锤靶向激励作用下的加速度响应特性进行分析，如图7与图8所示，其中，AR表示加速度响应(g)。

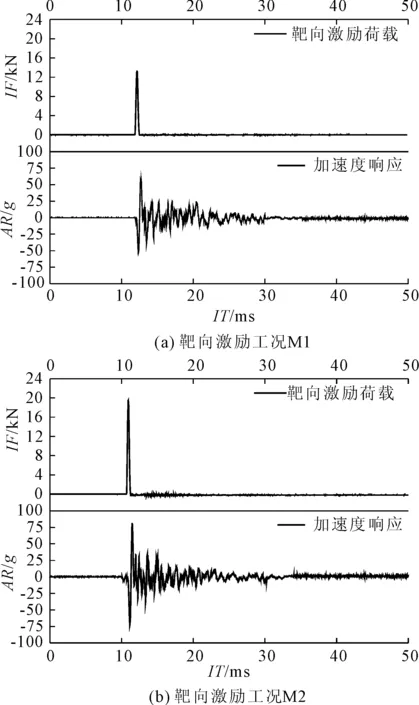
图7 PHPCCP1加速度响应特性

图8 PHPCRCP1加速度响应特性

据图7和图8可得模型PHPCCP1与PHPCRCP1在不同激励工况下的加速度响应特征参数见表4。

表4 加速度响应参数对比表

由表4分析表明：模型PHPCCP1靶向激励峰值荷载为13.341 kN时所形成的激励响应加速度最大峰值达到56.892g，最小峰值达到52.454g，靶向激励峰值荷载为19.546 kN时所形成的激励响应加速度最大峰值达到80.509g，最小峰值达到72.144g；模型PHPCRCP1靶向激励峰值荷载为14.606 kN时所形成的激励响应加速度最大峰值达到57.428g，最小峰值达到51.894g，靶向激励峰值荷载为20.253 kN时所形成的激励响应加速度最大峰值达到74.754g，最小峰值达到74.259g。

3 靶向激励下空间分布特征研究

3.1 靶向激励模式研究

基于激励位置模式特征代入公式(3)进行摆锤靶向激励模式的研究，结合不同激励工况下的靶向激励荷载特性试验所测相关参数，建立摆锤靶向激励模型，所得特征参数见表5。

表5 摆锤靶向激励模型的特征参数

根据表5中获得的不同激励工况下的靶向系数、激励频率，代入公式(3)分别可得模型PHPCCP1与PHPCRCP1在不同靶向激励下的靶向激励荷载历时曲线如图9所示。

图9 不同靶向激励下靶向激励荷载历时曲线

3.2 加速度空间分布特征分析

根据《混凝土设计规范》和《钢结构设计规范》，结合模型试验，得到摆锤靶向激励响应对比分析算例所用到的参数见表6与表7。

表6 算例模型力学性能参数

表7 算例模型摆锤靶向激励性能参数

由表6和表7中各个参数代入公式(24)得到模型PHPCCP1与PHPCRCP1在不同激励工况下的加速度响应空间分布特征如图10—图13所示。

图10 PHPCCP1-M1加速度空间分布特征

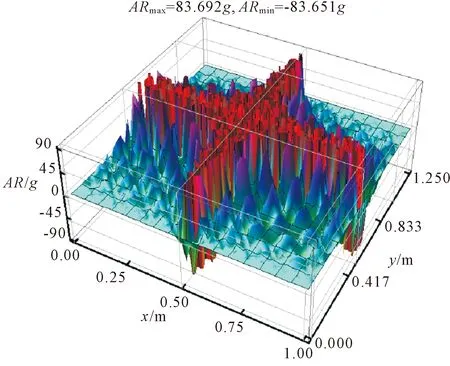
图11 PHPCCP1-M2加速度空间分布特征

图12 PHPCRCP1-M1加速度空间分布特征

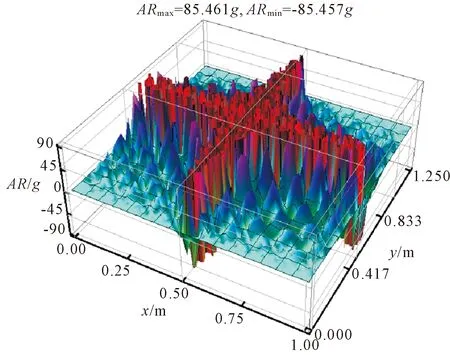
图13 PHPCRCP1-M2加速度空间分布特征

选取图10—图13中加速度空间分布的最大峰值与最小峰值进行对比，分析结果见表8。

表8 模型PHPCCP1与PHPCRCP1加速度响应峰值对比分析一览表

由表8分析可知：模型PHPCCP1在靶向激励M1作用下，加速度响应峰值误差在1.02～1.11之间，靶向激励M2作用下，加速度响应峰值误差在1.04～1.16之间；模型PHPCRCP1在靶向激励M1作用下，加速度响应峰值误差在1.03～1.14之间，靶向激励M2作用下，加速度响应峰值误差在1.14～1.15之间。综合表明：本文提出的摆锤靶向激励模式在分析水工高性能面板模型加速度响应空间分布特征时的整体误差在15%以内，吻合度高。进一步表明：在摆锤靶向激励作用下的水工高性能钢筋混凝土面板与水工高性能素混凝土面板的加速度空间分布特性的规律性一致。

4 结 论

提出摆锤靶向接触系数来表征靶向激励机理，推导出靶向激励响应解析解，建立了水工高性能钢筋混凝土面板靶向激励模型，完成了靶向激励响应试验研究与对比分析，结论如下：

(1) 提出靶向接触系数(ICC)，推导出水工高性能面板靶向激励控制微分方程，求解得到考虑时空效应的加速度响应函数表达式。

(2) 通过水工高性能面板靶向激励响应对比试验研究，找到了靶向激励能量试验实测值与理论计算值之间的关系，得到摆锤靶向激励模式在分析加速度空间分布特征时的总误差在16%以内。

(3) 基于水工高性能面板靶向激励响应空间分布特征分析，阐释得到在摆锤靶向激励作用下的水工高性能钢筋混凝土面板与水工高性能素混凝土面板表现出相同的靶向激励加速度空间分布规律。